کاربرد معادلات دیفرانسیل در زندگی
کاربرد ریاضی در زندگی
دراین مقاله سعی شده است که ارتباط دروس کتب ریاضی راهنمایی با سایر علوم و همچنین کاربرد آنها در دنیای امروز ی تا حدودی بررسی شود و ارائه گردد . بین رشته های علمی ، که بشر در طول هزاران سال به وجود آورده ، ریاضیّات جای مخصوص و ضمناٌ مهمّی را اشغال کرده است . ریاضیّات با علوم فیزیک ، زیست شناسی ، اقتصاد و فنون مختلف فرق دارد . با وجود این به عنوان یکی از روشهای اصلی در بررسیهای مربوط به کامپیوتر ، فیزیک ، زیست شناسی ، صنعت واقتصاد بکار می رود ودرآینده بازهم نقش ریاضّیات گسترش بیشتری می یابد. با وجود این مطلب ، برای آموزش جوانان هنوز از همان روشی استفاده می شود که سقراط و افلاطون ، حقایق عالی اخلاقی را برای شیفتگان منطق و فلسفه و برای علاقمندان سخنوری و علم کلام بیان می کردند . در حقیقت در درسهای حساب ، هندسه و جبر ،هرگز لزوم یادگیری آنها برای زندگی عملی خاطر نشان نمی شود. هرگز از تاریخ علم صحبتی به میان نمی آید. نظریه های سنگین علمی ، ولی هیچ نتیجه ای جز این ندارد که دانش آموزان را از علم بری کند و عدّه ی آنها را تقلیل دهد . یکی ازراههای جدی برای حلّ مسئله توجه به تاریخ علم، گفتگو در باره ی مردان علم و ارتباط ریاضی با عمل است ، ارتباطی که در تمام دوران زندگی بشر هرگز قطع نشده است . ● کاربرد ارقام در زمانهای قدیم هر قدمی که در راه پیشرفت تمدّن برداشته می شد، بر لزوم استفاده از اعداد می افزود . اگر شخصی گله ای از گوسفندان داشت ، می خواست آن را بشمرد ،یا اگر می خواست معبد یا هرمی بسازد ، باید می دانست که چقدر سنگ برای آن لازم دارد . اگر دارای زمین بود ، می خواست آن رااندازه گیری کند . اگر قایقش را به دریا می راند ، می خواست فاصله ی خود را از ساحل بداند . و بالاخره در تجارت و مبادله ی اجناس در بازارها ، باید ارزش اجناس حساب می شد.هنگامی که آدمی محاسبه با ارقام را آموخت ، توانست زمان ، فاصله مساحت ، حجم را اندازه گیری کند . با بکار بردن ارقام ، انسان بردانش و تسلّط خود بر دنیای پیرامونش افزود . ● کاربرد توابع و روابط بین اعداد کاربرد روابط بین اعداد و توابع و نتیجه گیریهای منطقی در نوشتن الگوریتمها و برنامه نویسی کامپیوتری است . مفهوم تابع یکی از مهمترین مفاهیم ریاضی است و در اصل تابع نوعی خاص از رابطه های بین دو مجموعه است . و با توجه به این که دنباله ها هم حالت خاصی از تابع است – تابعی که دامنه آن مجموعه ی اعداد { . . . و ۲ و ۱ و ۰ } است – دنباله های عددی در ریاضی و کامپیوتر کاربرد فراوان دارند . برای ساخت یک برنامه اساساٌ چهار مرحله را طی می کنیم : ۱) تعریف مسئله ۲) طراحی حل ۳) نوشتن برنامه ۴) اجرای برنامه لازم به ذکر است ...
کاربرد ریاضی
ریاضیات به عنوان یک درس اصلی است که داشتن درک درست از آن در آینده ی تحصیلی دانش آموزان و طبعاً پیشرفت علمی کشور نقش مهمی دارد . همچنین شامل کلیه ارتباطات ریاضی با زندگی روزمرّه ، سایر علوم و کاربردهایی در زندگی علمی آینده ی دانش آموزاست .به این ترتیب دربرنامه درسی و آموزشی ، برقرار کردن پیوند ریاضیات با کاربردهایش در زندگی و سایر علوم از قبیل :هنر،علوم طبیعی ،علوم اجتماعی و . . . . باید مدّ نظر قرار گیرد . در صورتی که این موارد در آموزش دیده نشود ، این سؤ ال همیشه در ذهن دانش آموز باقی می ماند که: « به چه دلیل باید ریاضی خواند ؟ » و« ریاضی به چه درد می خورد ؟ » دراین مقاله سعی شده است که ارتباط دروس کتب ریاضی راهنمایی با سایر علوم و همچنین کاربرد آنها در دنیای امروز ی تا حدودی بررسی شود و ارائه گردد . بین رشته های علمی ، که بشر در طول هزاران سال به وجود آورده ، ریاضیّات جای مخصوص و ضمناٌ مهمّی را اشغال کرده است . ریاضیّات با علوم فیزیک ، زیست شناسی ، اقتصاد و فنون مختلف فرق دارد . با وجود این به عنوان یکی از روشهای اصلی در بررسیهای مربوط به کامپیوتر ، فیزیک ، زیست شناسی ، صنعت واقتصاد بکار می رود ودرآینده بازهم نقش ریاضّیات گسترش بیشتری می یابد. با وجود این مطلب ، برای آموزش جوانان هنوز از همان روشی استفاده می شود که سقراط و افلاطون ، حقایق عالی اخلاقی را برای شیفتگان منطق و فلسفه و برای علاقمندان سخنوری و علم کلام بیان می کردند . در حقیقت در درسهای حساب ، هندسه و جبر ،هرگز لزوم یادگیری آنها برای زندگی عملی خاطر نشان نمی شود. هرگز از تاریخ علم صحبتی به میان نمی آید. نظریه های سنگین علمی ، ولی هیچ نتیجه ای جز این ندارد که دانش آموزان را از علم بری کند و عدّه ی آنها را تقلیل دهد . یکی ازراههای جدی برای حلّ مسئله توجه به تاریخ علم، گفتگو در باره ی مردان علم و ارتباط ریاضی با عمل است ، ارتباطی که در تمام دوران زندگی بشر هرگز قطع نشده است . ● کاربرد ارقام در زمانهای قدیم هر قدمی که در راه پیشرفت تمدّن برداشته می-شد، بر لزوم استفاده از اعداد می افزود . اگر شخصی گله ای از گوسفندان داشت ، می خواست آن را بشمرد ،یا اگر می خواست معبد یا هرمی بسازد ، باید می دانست که چقدر سنگ برای آن لازم دارد . اگر دارای زمین بود ، می خواست آن رااندازه گیری کند . اگر قایقش را به دریا می راند ، می خواست فاصله ی خود را از ساحل بداند . و بالاخره در تجارت و مبادله ی اجناس در بازارها ، باید ارزش اجناس حساب می شد.هنگامی که آدمی محاسبه با ارقام را آموخت ، توانست زمان ، فاصله مساحت ، حجم را اندازه گیری کند . با بکار بردن ارقام ، انسان بردانش و تسلّط ...
معادلات دیفرانسیل
مقدمه معادله دیفرانسیل معادلهای است که شامل یک یا چند مشتق یا دیفرانسیل باشد. معادلات دیفرانسیل بر اساس ویژگیهای زیر رده بندی میشوند: نوع (عادی یا جزئی) معادله شامل متغیر مستقل x ، تابع (y = f(x و مشتقات f را یک معادله دیفرانسیل عادی مینامیم. معادله ای متشکل از یک تابع مجهول با بیش از یک متغیر مستقل همراه با مشتقات جزئی آن معادله دیفرانسیل جزئی می نامیم. مرتبه که عباترت است از مرتبه مشتقی که بالاترین مرتبه را در معادله دارد. درجه نمای بالاترین توان مشتقی که بالاترین مرتبه را در معادله دارد، پس از حذف مخرج کسرها و رادیکالهای مربوط به متغیر وابسته و مشتقاتش. معمولا یک معادله دیفرانسیل مرتبه n جوابی شامل n ثابت دلخواه دارد، این جواب را جواب عمومی مینامند. ساختار معادلات دیفرانسیل ساختارهای متفاوتی هستند و هر ساختار ویژگیهای متفاوتی دارد:معادلات مرتبه اول از درجه اول با متغیرهای جدایی پذیر همگن خطی (برنولی) با دیفرانسیلهای کامل معادلات مرتبه دوم معادلات خطی با ضرایب ثابت: الف) همگن ب) ناهمگن. تکنیکهای تقریب زدن: الف) سریهای توانی ب) روشهای عددی. صور مختلف معادلات دیفرانسیل معادله دیفرانسیل مرتبه اول از درجه اول را همواره میتوان به صورت زیر در آورد که در آن M و N معرف توابعی از x و y هستند.Mdx + Ndy = 0در معادله فوق هرگاه M فقط تابعی از x و N فقط تابعی از y باشد. به صورت معادله جدایی پذیر مرتبه اول است. در این صورت با انتگرال گیری از هر جمله جواب بدست میآید. یعنی:M(x) dx+ ∫N(y) dy = C∫ معادله دیفرانسیل همگن گاه معادله دیفرانسیلی را که متغیرهایش جدایی پذیر نیستند با تعویض متغیر میتوان به معادلهای تبدیل کرد که متغیرهایش جدایی پذیر باشند، چنین معادلهای را همگن مینامند. معادله دیفرانسیل خطی مرتبه اول را همیشه میتوان به صورت متعارف زیر در آورد که در آن P و Q توابعی از x هستند.dy/dx + py = Qمعادله را که بتوان آن را به صورت: M (x,y) dx + N(x,y) dy = 0نوشت و دارای ویژگی زیر باشد کامل نامیده میشود. زیرا طرف چپ آن یک دیفرانسیل کامل است.M/∂y = ∂N/∂x∂ معادلات دیفرانسیل مرتبه دوم یک معادله دیفرانسیل مرتبه دوم در حالت کلی به صورت زیر است:F (x,y,dy/dx,d2y/dx2) = 0این گونه معادلات را معمولا با یک متغیر مناسب مثل dy/dx = p به معادلات دیفرانسیل نوع اول تبدیل کرد و با جاگذاری در معادله مربوط به روش معادلات دیفرانسیل مرتبه اول حل کرد. معادلات دیفرانسیل خطی معادله دیفرانسیل را که در آن توابع ، ، ... ، و بر بازه I پیوسته بوده و (an(x هرگز صفر نباشد یک معادله دیفرانسیل خطی مرتبه n ام مینامیم. که البته اگر در تعریف فوق (F(x مساوی صفر باشد، معادله دیفرانسیل ...
کاربرد ریاضی در زندگی بشر ( 1 )

کاربرد ریاضی در زندگی بشر (۱) به نام افریننده ای که درافرینش یک ها یگانه ودر بهم امیختن اعداد بی همتاست . مقدمه: علم لقمه برگرفتن از سفره طبیعت است . و ریاضی زاییده احتیاج و در آغازمبتنی بر تجربه. ریاضیات انعکاس دنیای واقعی در ذهن ماست. به عقیده بعضیها :ریاضیات زیباترین زبان برای توصیف طبیعت و روابط بین پدیدههای طبیعی است. سیلوستر میگوید:"ریاضیات ،مطالعه شباهتها در تفاوتها و مطالعه تفاوتها درشباهتهاست." *علت اساسی موفقیت ریاضیدانان در آفریدن علمی به این زیبایی که عمیقترین معرفت بشری شمرده میشود:سختگیری بدون بخشش کوچکترین خطاها در کنار روش و معیارهای منطقی آنها به همراه جدیت ، خلاقیت ، به غایت اندیشیدن و نیز بلند پروازی و جسارت شکستن هر چه موجود است. به هر قسمت از زندگی که کنجکاوانه و با دقت بنگریم ، اثر مستقیم یا غیر مستقیم ریاضیات در آن مشاهده میکنیم. نمونه آن کشف اخیر این مساله توسط دانشمندان است که :" یکی از انواع حشرات که بر روی شاخ و برگ درختان لانه سازی میکند، روش کارش بر اساس یک فرمول پیچیده ریاضی است." در حالت کلی ریاضیات راه های متعددی برای باز شدن فکر در اختیار ما قرار دارد که از مهمترین آنها مطالعه ی ریاضیات از جمله شاخه ی تر کیبیات است.ریاضیات این کمک را به ما میکند تا مشکلات و موضوعات زندگی را بهتر و راحت تر تجزیه و تحلیل کنیم. ** *ارزنده نیا.محمد،الفبای طبیعت، نشر سپیده،اول ،ص7 ** همان،ص9 آمارهای جهانی نشان می دهد طلاق در خانواده هایی که حداقل یکی از همسران ریاضی خوانده است در مقایسه با سایر خانواده ها بسیار کمتر است. زندگي مثل رياضيات است پس بيا غم هايش را تقسيم . بدي هايش را تفريق خوبي هايش راجمع مهرباني هايش را ضرب كنيم . ساختار جبر مجرد نظریه اعداد نظریه گروهها توپولوژی نظریه مدولها نظریه ترتیبجبر مجرد، نظریه اعداد، هندسه جبری، نظریه گروهها، مونوئیدها، آنالیز ریاضی، آنالیز تابعی، توپولوژی، جبر خطی، نظریه گراف، جبر عمومی، نظریه مدولها، نظریه ترتیب، نظریه مزورمشابهت زندگی اجتماعی وعرصه ریاضیات زندگي انسان ها يك تابع رياضي است و از قوانين رياضي تبعيت مي كند. با اينكه رياضيات تنها علمي است كه توسط بشر ايجاد شده است و علمي است منطقي ، نه مشاهداتي و تجربي ، اما همگان مي دانند كه تقريباً قوانين تمامي علوم طبيعي و قوانين مربوط به حركات اجرام آسماني و گذر زمان و ساير قوانين طبيعت هريك به نوعي از قوانين رياضي تبعيت مي كنند. چرا كه رياضيات نيز خود آفريده پنهان خداوند در بطن طبيعت است. بگذريم Y به x زندگي انسانها نيز همانند توابعي كه در دبيرستان خوانده ...
کاربرد ریاضی در زندگی بشر (۲)

کاربرد ریاضی در زندگی بشر (۲) استفاده از عدد پي در ساخت تخت جمشيد مهندسان هخامنشی راز استفاده از عدد پی (۱۴/۳ ) را دو هزار و 500 سال پیش کشف کرده بودند. آنها در ساخت سازه های سنگی و ستون های مجموعه تخت جمشید که دارای اشکال مخروطی است، از این عدد استفاده می کردند.عدد پی( ۳.۱۴)در علم ریاضیات از مجموعه اعداد طبیعی محسوب می شود. این عدد از تقسیم محیط دایره بر قطر آن به دست می آید. کشف عدد پی جزو مهمترین کشفیات در ریاضیات است. کارشناسان ریاضی هنوز نتوانسته اند زمان مشخصی برای شروع استفاده از این عدد پیش بینی کنند. عده زیادی، مصریان و برخی دیگر، یونانیان باستان را کاشفان این عدد می دانستند اما بررسی های جدید نشان می دهد هخامنشیان هم با این عدد آشنا بودند.«عبدالعظیم شاه کرمی» متخصص سازه و ژئوفیزیک و مسئول بررسی های مهندسی در مجموعه تخت جمشید در این باره، گفت: «بررسی های کارشناسی که روی سازه های تخت جمشید به ویژه روی ستون های تخت جمشید و اشکال مخروطی انجام گرفته؛ نشان می دهد که هخامنشیان دو هزار و 500 سال پیش از دانشمندان ریاضی دان استفاده می کردند که به خوبی با ریاضیات محض و مهندسی آشنا بودند. آنان برای ساخت حجم های مخروطی راز عدد پی را شناسایی کرده بودند.»*دقت و ظرافت در ساخت ستون های دایره ای تخت جمشید نشان می دهد که مهندسان این سازه عدد پی را تا چندین رقم اعشار محاسبه کرده بودند. شاه کرمی در این باره گفت: «مهندسان هخامنشی ابتدا مقاطع دایره ای را به چندین بخش مساوی تقسیم می کردند. سپس در داخل هر قسمت تقسیم شده، هلالی روتانا.البوث،کاربرد ریاضیات،علی رعنایی،امیرکبیر،اول،ص65 معکوس را رسم می کردند. این کار آنها را قادر می ساخت که مقاطع بسیار دقیق ستون های دایره ای را به دست بیاورند. محاسبات اخیر، مهندسان سازه تخت جمشید را در محاسبه ارتفاع ستون ها، نحوه ساخت آنها، فشاری که باید ستون ها تحمل کنند و توزیع تنش در مقاطع ستون ها یاری می کرد. این مهندسان برای به دست آوردن مقاطع دقیق ستون ها مجبور بودند عدد پی را تا چند رقم اعشار محاسبه کنند.»هم اکنون دانشمندان در بزرگ ترین مراکز علمی و مهندسی جهان چون «ناسا» برای ساخت فضاپیماها و استفاده از اشکال مخروطی توانسته اند عدد پی را تا چند صد رقم اعشار حساب کنند. بر اساس متون تاریخ و ریاضیات نخستین کسی که توانست به طور دقیق عدد پی را محاسبه کند، «غیاث الدین محمد کاشانی» بود. این دانشمند اسلامی عدد پی را تا چند رقم اعشاری محاسبه کرد. پس از او دانشمندانی چون پاسکال به محاسبه دقیق تر این عدد پرداختند. هم اکنون دانشمندان با استفاده از رایانه های بسیار پیشرفته به محاسبه این ...
کاربرد لگاریتم در زندگی
نظریه ها و قاعده های ریاضی، با کشف خود «هستی» پیدا می کنند، آن ها تنها وجود دارند و اغلب بدون کاربردند. دیر یا زود، و گاهی بعد از صدها و هزارها سال، این موجودات ریاضی به «صفت» تبدیل می شوند و کاربرد خود را در زندگی و عمل، در سایر دانش ها، در صنعت و هنر پیدا می کنند.«اویلر» ¼br> ¼br> شاید ۳۸۰ سال پیش کسی فکر نمی کرد لگاریتمی که در رابطه با نیاز محاسبات عملی کشف شد در آینده کاربردهای وسیعی پیدا کند.شاید هیچوقت کپلر فکر نمی کرد که جدول هایی را که برای ساده کردن محاسبات طولانی در تعیین مدار مریخ و یا کارهای اخترشناسی دیگرش تنظیم کرد، جرقه ای این چنین را در ریاضیات ایجاد کند.یا شاید لاپلاسی که گفت: “لگاریتم طول زندگی اخترشناسان را چند برابر کرد” نمی دانست که نه تنها طول زندگی اخترشناسان بلکه دریانوردان، بازرگانان، موسیقیدانان، شیمیدانان، ریاضیدانان، زمین شناسان و حتی همه ی انسان های کره ی زمین را چند برابر کرد.بدیهی است که تا نیاز به چیزی احساس نشود آن چیز کشف و اختراع نمی گردد، در واقع هرکدام از علومی که با آن روبه رو هستیم هریک به مقتضای نیازی و با توجه به هدف خاصی پیکر بندی شده اند.لگاریتم نیز با توجه به محاسبه های طولانی و ملال آوری که دانشمندان سده های شانزدهم و هفدهم میلادی با آن سر و کار داشتند، بوجود آمد. این محاسبه ها وقت و نیروی زیادی را از دانشمندان تلف می کرد و همیشه دانشمندان در ذهن داشتند که چطور می شود بدون انجام چنین محاسبات پیچیده و دشواری و آن هم در کمترین زمان ممکن به جواب مطلوب دست یابند. گفته می شود که حتی در قرن هشتم هندی ها با محاسبات مربوط به لگاریتم آشنایی داشتند اما این کلمه و مفهوم مربوط می شود به قرن شانزدهم .جدول هایی نیز در این زمینه بوجود آمد و شاید همین تلاش ها و نیازها بود که سر انجام به کشف لگاریتم انجامید تا آن جا که دو دانشمند به طور همزمان و بدون اینکه از کار یکدیگر آگاه باشند موفق به کسب چنین افتخاری گشتند اولی جان نپر و دیگری بورگی.اما اصطلاح لگاریتم نشات گرفته از فعالیت های نپر است که از واژه ی یونانی «لوگوس» به معنی نسبت و «ارتیوس» به معنی عدد گرفته شده است. او همچنین بجای لگاریتم از اصطلاح عدد ساختگی نیز استفاده می کرد. نپر چکیده ی کارهای خود را در کتابی با عنوان «شرح جدول های عجیب لگاریتمی» چاپ کرد و به دنیا نمایاند.عدد e (مبنای لگاریتم طبیعی) نیز در چنین سال هایی چشم به جهان و جهانیان گشود. گفته می شود کاشف عددe آن گونه که برخی می پندارنداویلر نبوده است بلکه خود نپر بحث مربوط به لگاریتم طبیعی و عدد e را در یکی از نوشته هایش پیش کشیده است.بعد از آشکار شدن لگاریتم به ...
کاربرد جبر در کوانتوم
١- آمار و احتمال(Statistic & Probability)این علم به بررسی رخدادهای غیر قطعی که در عین حال فضای نمونه (کلیه حالتهای ممکن رخداد اتفاق) مشخص دارند می پردازد.مثلا در پرتاب یک سکه نمیدانید شیر می آید یا خط اما میدانید یا شیر می آید یا خط.مباحث اصلی این گرایش پرکاربرد ریاضی عبارتند از توزیعهای پیوسته و گسسته و توام نظریه نمونه گیری نظریه تصمیم نظریه برآورد آزمون فرض رگرسیون فرآیندهای تصادفی سریهای زمانی و ...2- آنالیز ریاضی(Mathematics Analysis)یکی از قدیمی ترین شاخه های ریاضیات است که پایه ی تئوری بسیاری از گرایشهای پرکاربرد ریاضی مثل آنالیز عددی را فراهم میکند.در این شاخه به آنالیز دقیق توابع حد مشتق انتگرال دنباله ها سری ها و توپولوژی مجموعه ها پرداخته می شود.3- آنالیز عددی(Numerical Analysis)کاربردی ترین شاخه علم ریاضی محسوب میشود و در واقع حلقه اتصال بین ریاضیات و علوم مهندسی بشمار می رود.این علم که مهندسان آن را با نام محاسبات عددی میشناسند دارای زیر شاخه های گوناگون مثل آنالیز خطا نظریه درونیابی و تقریب مشتق گیری و انتگرال گیری عددی حل معادلات یک و چند متغیره حل عددی معادلات دیفرانسیل معمولی و معادلات انتگرالی جبر خطی عددی و حل عددی معادلات با مشتقات جزئی (PDE) می باشد.4- بهینه سازی و تحقیق در عملیات(Optimization & Operation Research)یکی از شاخه های پر کاربرد ریاضیات در صنعت،بهینه سازی و تحقیق در عملیات می باشد.هدف این علم مدل بندی مسائل مرتبط با صنعت و بهینه سازی آنهاست مثلا ماکزیمم کردن سود یا مینیمم کردن هزینه ها با داشتن منابع محدود. مباحث گوناگون این علم شامل برنامه ریزی خطی برنامه ریزی صحیح برنامه ریزی پویا و برنامه ریزی غیر خطی و ... است.5- ترکیبیات(Combinatorics)این گرایش به بررسی دسته های معمولا متناهی اشیا و چگونگی چینش آنها می پردازد و کاربردهای زیادی در نظریه احتمال هندسه و جبر دارد.ترکیب ترتیب جایگشت اصل شمارش و روابط بازگشتی مباحث اصلی ترکیبیات هستند.6- توابع مختلط(Complex Functions)این گرایش به بررسی مباحث مرتبط با اعداد و توابع مختلط می پردازد. بحث مربوط به روابط جبری بین اعداد مختلط انواع توابع مختلط دنباله و سری اعداد مختلط حدگیری مشتق گیری و انتگرال گیری از توابع مختلط از جمله مباحث این گرایش می باشد.7- جبر(Algebra)یکی از کهن ترین و در عین حال قطعی ترین شاخه های ریاضیات محسوب میشود و پایه ی بسیاری از گرایشهای امروزی ریاضیات و حتی علوم غیر ریاضی بشمار می رود بگونه ای که متخصصان نظریه کوانتوم نیز از جبر استفاده میکنند.بخشهای مختلف جبر عبارتند از نظریه گروهها نظریه حلقه ها نظریه میدانها نظریه گالوا و ...8- جبرخطی(Linear Algebra)بسیاری از عملگرها ...
اطلس ریاضی: کاربردهای ریاضیات در علوم
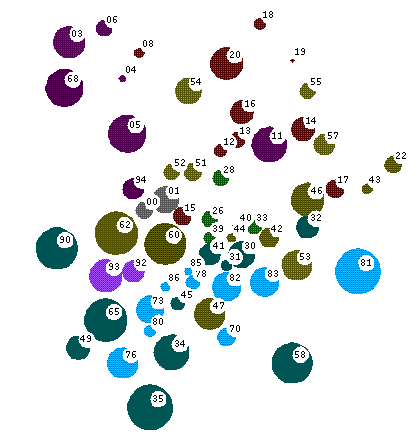
اطلس ریاضی: کاربردهای ریاضیات در علوم ترجمه: ابوالفضل گروئی - منبع: سایتwww.math.niu.edu * در صورت تمایل میتوانید اصل مقاله را در انتها مطالعه فرمائید. از نظر تاریخی، این نیازهای علوم فیزیکی بوده است که محرک توسعه بسیاری از قسمتهای ریاضیات، به ویژه آنالیز بوده اند. گاهی اوقات مشکل است که کاربردها را از نظر ریاضی طبقه بندی کرد، چرا که ابزارهائی از چند حوزه ریاضیات ممکن است به کار گرفته شده باشند. ما روی این کاربردها نه فقط با بحث درباره طبیعت نظم (و سازماندهی) آنها متمرکز میشویم، بلکه برهمکنش آنها با ریاضیات را نیز مد نظر قرار میدهیم. بیشتر حوزه ها در این گروه (نقاط آبی در تصویر) در مجموع با عنوان «فیزیک ریاضی» شناخته شده اند. تا اندازه ای، ابزارهای ریاضی جدیدتر و به طور پیشرونده پیچیده تر در مهندسی، زیست شناسی و علوم اجتماعی (نواحی بنفش در تصویر) به کار گرفته میشوند. 70- مکانیک ذرات و سیستمها: مطالعه دینامیک مجموعه های ذرات یا توده های جامد (تو پر)، شامل توده های چرخان یا لرزان. از اصول تغییرات (انرژی-کمینه سازی) همچنین معادلات دیفرانسیل استفاده میکند. Equilibrium in statistical mechanics: systems exchanging energy are most likely to have individual energies that maximize the overall number of states. (Image by Prof. Mehran Kardar.) تعادل در مکانیک آماری: سیستمهای مبادله کننده انرژی تمایل به داشتن انرژیهای مشخصی دارند که تعداد کل حالتها را بیشینه میکند (تصویر از پروفسور مهران کاردار از سایت: www.core.org.cn) 74- مکانیک توده های تغییر شکل پذیر: معادلات الاستیسیته و پلاستیسیته، انتشار موج، مهندسی و حوزه هائی در جامدات ویژه مانند خاکها و بلورها را در نظر میگیرد. مثالهای تغییر شکل کره: الف) شکل ابتدائی ب) کشش و پ) نیشگون گیری. 76- مکانیک سیالات: هوا، آب و دیگر سیالات در حال حرکت را بررسی میکند؛ همچنین: تراکم، اغتشاش، نفوذ، انتشار موج و غیره. از نظر ریاضی، مطالعه حلهای معادلات دیفرانسیل شامل روشهای عددی در مقیاس بالا (برای نمونه، روش اجزای محدود) را در بر میگیرد. Image by Bomphrey et al. (Phy. of Fluid 2002) بررسی رفتار سیال (هوا) در اطراف یک ملخ چرخان. تصویر از بامفری و همکاران (در مجله فیزیک سیال ۲۰۰۲). 78- نورشناخت (اپتیک)، تئوری الکترومغناطیس: بررسی انتشار و تغییر شکل امواج الکترومغناطیسی شامل مباحث تداخل و پراش است. در کنار شاخه های متداول آنالیز، این حوزه مباحث هندسی مانند مسیرهای پرتوهای نوری را نیز در بر میگیرد. انتهای رشته(فیبر)های نوری. 80- ترمودینامیک کلاسیک، انتقال گرما: بررسی شارش گرما از میان ماده شامل تغییر فاز و احتراق است. از نظر تاریخی منشاء سریهای «فوریه» است. نیمرخ (پروفایل) توزیع دما در لوله آب خنک ...
دانلود کتاب معادلات دیفرانسیل بویس
کتاب معادلات دیفرانسیل نوشته بویس از بهترین کتابهای معادلات برای دانشجویان فیزیک،که علاوه بر روشهای حل معادلات بر تحلیل جواب ها و دید فیزیکی انها هم تاکید داردhttp://toopfile.com/en/file/2617/boyce-w.e.-diprima-r.c..pdf.html
