کاربرد معادلات دیفرانسیل در اقتصاد
رزومه من
سوابق پژوهشی کنفرانس ها و همایش ها ۱-بکارگیری معادلات دیفرانسیل تصادفی در مدلسازی و پیش بینی تورم در اقتصاد ایران، دومین همایش دانشجویی اقتصاد ایران، دانشگاه مازندران، اردیبهشت 1390. 2- کاربرد معادلات دیفرانسیل تصادفی در مدل سازی و پیش بینی قیمت جهانی نفت خام، اولین کنفرانس بین المللی رویکردهای نوین در نگهداشت انرژی، دانشگاه امیرکبیر، آذر ماه 1390. دانلود 3-نگرش پویا بر ارزش در معرض خطر پورتفوی سهام بر پایه مدل های حالت فضا و فیلتر کالمن: مطالعه موردی بورس اوراق بهادار تهران ، سومین کنفرانس ریاضیات مالی و کاربردها ، 11 و 12 بهمن ماه 1391، سمنان. دانلود 4- Investigation the US Financial Crisis Contagion to Istanbul Stock Exchange:An Application of Bivariate GARCH Models, ICE-TEA 2012-Conference , Izmir , Turkey , 1-3 November , 2012. download 5. اخلاق و کارایی در بازارهای اسلامی بورس اوراق بهادار. هشتمین همایش دو سالانه اقتصاد اسلامی، اردیبهشت 1393، دانلود مقالات علمی - پژوهشی چاپ شده 1- بهینه سازی سبد سرمایه گذاری سهام بر اساس مدل های چندمتغیره ناهمسان واریانس : شواهدی از بورس اوراق بهادار تهران، مجله علمی پژوهشی تحقیقات مالی، دوره 12، شماره 30، صفحات 35-56، دانشکده مدیریت دانشگاه تهران ، (۱۳۸۹). دانلود 2- مدل سازی و پیش بینی نرخ ارز بر اساس معادلات دیفرانسیل تصادفی، مجله علمی پژوهشی تحقیقات اقتصادی دانشگاه تهران، دوره ۴۷، شماره ۳، صفحات ۱۲۹-۱۴۴ ، (۱۳۹۱). دانلود 3- مقایسه پیش بینی تورم بر اساس معادلات دیفرانسیل تصادفی با مدل های رقیب، مجله علمی پژوهشی پژوهشهای اقتصادی دانشگاه تربیت مدرس، 1392، سال 13، شماره 1، صص : 25-46. دانلود 4- مقایسه عملکرد مدل های ARFIMA-GARCH ، شبکه عصبی و معادلات دیفرانسیل تصادفی در پیش بینی قیمت جهانی نفت خام ، مجله مطالعات اقتصاد انرژی، شماره 36، (1392) ، دانلود 5- Dynamic portfolio Value at Risk estimation using DCC-MGARCH model, International SAMANM Journal of Finance and Accounting, Vol. 2 No. 1 , January 2014, ISC index Journal. Download 6. تاملی بر اجرای فاز دوم قانون هدفمندسازی یارانه ها با تمرکز بر سهم انرژی در تولید با استفاده از یک مدل تعادل عمومی پویای تصادفی ، فصلنامه پژوهشهای اقتصادی ایران، شماره 56 ، پاییز 92. دانلود 7. شوک های نفتی و سیاست پولی در ایران: شواهدی بر پایه یک مدل تعادل عمومی پویای تصادفی، فصلنامه پژوهشهای پولی و بانکی، 7 (19):51-67.دانلود 8- مدل سازی غیرخطی تاثیر مخارج دولت و منابع تامین مالی آن بر رشد اقتصادی: رهیافت رگرسیونی انتقال ملایم، فصلنامه علمی پژوهشی برنامه ریزی و بودجه ، پذیرش چاپ آتی. دانلود سوابق تدریس اقتصادسنجی - دوره کارشناسی دانشگاه ارومیهریاضیات (1) - مرکز آموزشهای نیمه حضوری دانشگاه ارومیه 1- تدریس ...
معادلات دیفرانسیل
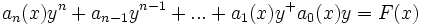
معادله دیفرانسیل معادلهای است بیانگر یک تابعی از یک یا چندین متغیر وابسته و مشتقهای مرتبه های مختلف آن متغیرها. بسیاری از قوانین عمومی طبیعت (در فیزیک، شیمی، زیستشناسی و ستارهشناسی) طبیعیترین بیان ریاضی خود را در زبان معادلات دیفرانسیل مییابند. کاربردهای معادلات دیفرانسیل همچنین در ریاضیات، بویژه در هندسه و نیز در مهندسی و اقتصاد و بسیاری از زمینههای دیگر علوم فراواناند. معادلات دیفرانسیل در بسیاری پدیده های علوم رخ می دهند. هر زمان که یک رابطه بین چند متغیر با مقادیر مختلف در حالت ها یا زمان های مختلف وجود دارد و نرخ تغییرات متغیرها در زمان های مختلف یا حالات مختلف شناخته شده است میتوان آن پدیده را با معادلات دیفرانسیل بیان کرد. به عنوان مثال در مکانیک، حرکت جسم بوسیله سرعت و مکان آن در زمان های مختلف توصیف می شود و معادلات نیوتن به ما رابطه بین مکان و سرعت و شتاب و نیروهای گوناگون وارده بر جسم را میدهد. در چنین شرایطی می توانیم حرکت جسم را در قالب یک معادله دیفرانسیل که در آن مکان ناشناخته جسم تابعی از زمان است بیان کنیم. شاخه بندی متدهای حل معادلات دیفرانسیل بسیار مرتبط با نوع معادله هستند. معادلات دیفرانسیل را به طور کلی به دو دسته می توان تقسیم کرد. معادلات دیفرانسیل عادی: در این نوع معادلات تابع جواب دارای تنها یک متغیر مستقل است. معادلات دیفرانسیل جزیی: در این نوع معادلات تابع جواب دارای چندین متغیر مستقل می باشد. هر دو نوع این معادلات را می توان از دیدگاه خطی یا غیر خطی بودن تابع جواب هم دسته بندی کرد. معادلات دیفرانسیل مشهور قانون دوم نیوتن در مکانیک معادلات همیلتون در مکانیک کلاسیک معادلات ماکسولدر الکترو مغناطیس معادلات پواسن مسئله منحنی کوتاهترین زمان. فرمول انیشتین. قانون گرانش نیوتن. معادله موج برای تار مرتعش. نوسانگر همساز در مکانیک کوانتومی. نظریه پتانسیل. معادله موج برای غشای مرتعش. معادلات شکار و شکارچی. مکانیک غیر خطی. مسئلهٔ مکانیکی آبل. نوع(عادی یا جزئی) معادله شامل متغیر مستقل x ، تابع (y = f(x و مشتقات f را یک معادله دیفرانسیل عادی مینامیم.معادله ای متشکل از یک تابع مجهول با بیش از یک متغیر مستقل همراه با مشتقات جزئی آن معادله دیفرانسیل جزئی می نامیم. مرتبه که عباترت است از مرتبه مشتقی که بالاترین مرتبه را در معادله دارد. درجه نمای بالاترین توان مشتقی که بالاترین مرتبه را در معادله دارد، پس از حذف مخرج کسرها و رادیکالهای مربوط به متغیر وابسته و مشتقاتش. معمولا یک معادله دیفرانسیل مرتبه n جوابی شامل n ثابت دلخواه دارد، این جواب را جواب عمومی مینامند. ساختار معادلات ...
دانلود کتاب معادلات دیفرانسیل از دکتر مسعود نیکوکار

دانلود کتاب معادلات دیفرانسیل از دکتر مسعود نیکوکار نام کتاب : معادلات دیفرانسیلنام نویسنده : دکتر مسعود نیکوکارزبان : پارسیتعداد صفحه : 527قالب : PDFحجم : 33.6 معادله دیفرانسیل معادلهای است بیانگر یک تابعی از یک یا چندین متغیر وابسته و مشتقهای مرتبههای مختلف آن متغیرها. بسیاری از قوانین عمومی طبیعت ( در فیزیک، شیمی، زیستشناسی و ستارهشناسی ) طبیعیترین بیان ریاضی خود را در زبان معادلات دیفرانسیل مییابند. کاربردهای معادلات دیفرانسیل همچنین در ریاضیات، بویژه در هندسه و نیز در مهندسی و اقتصاد و بسیاری از زمینههای دیگر علوم فراواناند. معادلات دیفرانسیل در بسیاری پدیدههای علوم رخ می دهند. هر زمان که یک رابطه بین چند متغیر با مقادیر مختلف در حالتها یا زمانهای مختلف وجود دارد و نرخ تغییرات متغیرها در زمانهای مختلف یا حالات مختلف شناخته شده است میتوان آن پدیده را با معادلات دیفرانسیل بیان کرد. به عنوان مثال در مکانیک، حرکت جسم بوسیله سرعت و مکان آن در زمانهای مختلف توصیف میشود و معادلات نیوتن به ما رابطه بین مکان و سرعت و شتاب و نیروهای گوناگون وارده بر جسم را میدهد. در چنین شرایطی می توانیم حرکت جسم را در قالب یک معادله دیفرانسیل که در آن مکان ناشناخته جسم تابعی از زمان است بیان کنیم. سرفصلهای کتاب :معادلات دیفرانسیل معمولیمعادلات دیفرانسیل مرتبه اولمعادلات دیفرانسیل معمولی مرتبه دوم و بالاترحل معادلات با استفاده از سریهادستگاه معادلات دیفرانسیل خطیتبدیل لاپلاس برای دانلود با حجم 33.6 MB کلیک کنید
بررسی ریاضیات در آموزش اقتصاد (1)

فصلنامه اقتصاد مقداري، دوره 5، شماره 3، پاییز 1387 باقر درویشی، محمدنبی شهیکی تاش و دکتر حسین محمدي1مقدمه اقتصادریاضیدرواقعابزارریاضیبرايتحلیلمطالبوبیانتئوريهاياقتصاداست. ریاضیاتبهعنوانمنطقتفکرواقتصادبهعنوانمنطقعلمیانتخابهستند. ترکیبایندویعنیاقتصادریاضی،تأثیربسزاییدرالگوسازي هايمرتبطباانتخاببهینهدراقتصادداشتهاست. درنگرشمکتبنئوکلاسیک،استفادهازریاضیاتبهعنوانابزارتحلیلاقتصادمطرحشدوتحتتأثیرطرفداراناثباتگراییقرارگرفتکهمعتقدبودندهرمعرفتیکهبخواهدعلممحسوبشود،بایدبتواندگزارهيخودرابهصورتتجربیآزمونکندیابهشکلریاضیدرآورد(چیانگ (1371،3 ریاضیاتدرتمامیشاخههايعلماقتصادنقشمهمیراایفامیکندو امروزهکمتراقتصاددانیوجودداردکهبتواندخودراازکاربردریاضیاتدرتشریحمباحثومسائلاقتصاديوبهخصوصموضوعاتنظرياقتصادبینیازبداند. درحالحاضر،ریاضیاتبهعنوانابزاريبرايتحلیلمسائلوپدیدههاياقتصاديشناختهمیشودوازآنجاکهاقتصادریاضیصرفاًیکروشتحلیل اقتصادياست،اصولآنباروشهايغیرریاضیتحلیلاقتصاديتفاوتیندارد. همیشههدفازهرگونهتحلیلنظري،صرفنظرازروشکار،بهدست آوردنمجموعهايازنتایجوقضایاییاستکهبااستفادهازاستدلالمنطقیازمجموعهايازفرضها،حاصلمیشود. تفاوتعمدهياقتصادریاضیبااقتصادتشریحیایناستکهدراقتصاد ریاضیفرضیههاونتایجبهوسیلۀ نمادهايریاضی (بهجايکلمات(ومعادلات )بهجايجملات)بیانمیشوند. بهعلاوه،بهجايمنطقتشریحی،ازقضایاي ریاضیدراستدلالاستفادهمیشود. میتوانادعانمودکهکاربردنمادهايریاضی،استدلالقیاسیراراحتترمیکندوباکمکآنمیتوانفرضیههاراروشنترودقیقتربیاننمود. بهطورخلاصهروشریاضیدارايمزایايزیراست: 1- زبان بهکاربردهشدهدقیقتروصریحتراست. -2 قضایاوروابطریاضیزیاديبراياستفادهوجوددارند. -3 اجبارتحلیلگردربیانصریحتمامفرضهابهعنوانشرطلازمبراي کاربردتحلیلریاضی،ازانتخابناخودآگاهفرضهايغیرصریحوغیرضروري جلوگیريمیکند. 4- امکان می دهد که حالت های کلی n متغیره تحلیل شود.(پور کاظمی،1381) آشناییبامباحثریاضیاتوحدومرزآن،برايیکاقتصاددانالزامی است. دراینمقالهسعیشدهاستکهبامروريبرتاریخچهياقتصادریاضیومعرفیمهمترینتکنیکهاوابزارهايموردنیازبرايدانشجویانواساتیداقتصاد،کاربردآنهاذکرشود. درپایاننیزبهارزیابیمیزانتسلطدانشجویاناقتصاددرمورداینمسایلپرداختهشدهاست. -2 تاریخچهيبهکارگیريریاضیاتدراقتصاد تلاشکورنو4 برايکاربردریاضیاتدراقتصاد،بهعنوانحرکتآغازینتلقی میشودوبخشیازادبیاتاولیۀاقتصادریاضیتوسطويارائهشد ...
اقتصــــــاد ریاضــــــی
اقتصــــــاد ریاضــــــیامروزه علم اقتصاد با گسترش و رشد قابل توجه به صورت یک موضوع ریاضی تبدیل شده است. ریاضیات موجود در نوشته های اقتصادی ۵۰ سال گذشته که به عنوان ریاضیات پیش رفته تلقی شده بودند، اکنون از آن به عنوان زبان معمولی تشریح مباحث اقتصادی یاد می شود. ریاضیات در تمام شاخه های مختلف علم اقتصاد و سایر علوم اجتماعی نقش مهمی را ایفا می کند. امروزه کمتر اقتصاددانی وجود دارد که بتواند خود را از کاربرد ریاضیات در تشریح مباحث و مسائل اقتصادی و به خصوص موضوعات نظری اقتصاد که در حقیقت پایه ی بررسی های تجربی اقتصاد سنجی در این رشته را تشکیل می دهند، بی نیاز بداند. بنابراین اقتصاد ریاضی را نمی توان مانند اقتصاد بخش عمومی ویا اقتصاد بین الملل به عنوان شاخه ی مستقلی از علم اقتصاد تلقی نمود. بلکه باید آن را به عنوان ابزاری برای تحلیل مسائل و پدیده های اقتصادی محسوب نمود.اهمیت اقتصاد ریاضیاز دیرباز، دانش ریاضیات امکانات مناسبی را به منظور ارائه ی تحلیل های دقیق، توصیف روابط بین پدیده ها و نیز کاهش خطای پیش بینی در اختیار علوم مختلف قرار داده است. ماهیت کمی بیش تر متغیرهای اقتصادی در کنار عواملی مانند لزوم برنامه ریزی و … سبب توسعه ی کاربرد ریاضیات در اقتصاد گردیده است. ساده سازی و رعایت ایجاز و اختصار در ارائه ی نظریه های اقتصادی و به خصوص دقت بالای این ابزار موجب شده است که اقتصاددانان از ریاضیات به عنوان ابزاری به منظور ارائه ی نظریه هایشان استفاده نمایند. بنابراین اقتصاد ریاضی، مانند اقتصاد سنجی شاخه ای مستقل در دانش اقتصاد مانند اقتصاد خرد یا اقتصاد کلان محسوب نمی شود بلکه اقتصاد ریاضی یک ابزار تحقیق و یک زبان برای ارائه ی نظریه های اقتصادی محسوب می شود.برای بیان اهمیت نقش ریاضیات در اقتصاد، می توان به موارد زیر اشاره کرد: کاربرد ریاضیات محض در نظریه های اقتصادیدر این ارتباط، کافی است به این مطلب اشاره شود که بیشتر اقتصاددانان مهم و برجسته ی صد سال گذشته، ریاضی دان بوده اند. آلفرد مارشال، ویلیام استانی جونز، نات ویکسل و جان مینارد کینز از جمله ی این اقتصاددانان هستند. در حالی که اقتصاددانان دیگری نیز وجود دارند که علم اقتصاد را در تحلیل های خود با منطق آمیخته اند. از جمله می توان به ژان استوارت میل و ری هارود اشاره کرد. در رابطه با این که چرا زبان ریاضی بر زبان معمول در اقتصاد می تواند مزیت داشته باشد، باید به دلایل زیر اشاره نمود: الف. اصطلاحات و عبارات ریاضی دقیق بوده و کمتر گمراه کننده اند در زبان معمول (نوشتاری)، یک واژه ممکن است معانی و تفاسیر مختلفی داشته باشد که هر یک از این تفاسیر ...
کاربرد ریاضی
ریاضیات به عنوان یک درس اصلی است که داشتن درک درست از آن در آینده ی تحصیلی دانش آموزان و طبعاً پیشرفت علمی کشور نقش مهمی دارد . همچنین شامل کلیه ارتباطات ریاضی با زندگی روزمرّه ، سایر علوم و کاربردهایی در زندگی علمی آینده ی دانش آموزاست .به این ترتیب دربرنامه درسی و آموزشی ، برقرار کردن پیوند ریاضیات با کاربردهایش در زندگی و سایر علوم از قبیل :هنر،علوم طبیعی ،علوم اجتماعی و . . . . باید مدّ نظر قرار گیرد . در صورتی که این موارد در آموزش دیده نشود ، این سؤ ال همیشه در ذهن دانش آموز باقی می ماند که: « به چه دلیل باید ریاضی خواند ؟ » و« ریاضی به چه درد می خورد ؟ » دراین مقاله سعی شده است که ارتباط دروس کتب ریاضی راهنمایی با سایر علوم و همچنین کاربرد آنها در دنیای امروز ی تا حدودی بررسی شود و ارائه گردد . بین رشته های علمی ، که بشر در طول هزاران سال به وجود آورده ، ریاضیّات جای مخصوص و ضمناٌ مهمّی را اشغال کرده است . ریاضیّات با علوم فیزیک ، زیست شناسی ، اقتصاد و فنون مختلف فرق دارد . با وجود این به عنوان یکی از روشهای اصلی در بررسیهای مربوط به کامپیوتر ، فیزیک ، زیست شناسی ، صنعت واقتصاد بکار می رود ودرآینده بازهم نقش ریاضّیات گسترش بیشتری می یابد. با وجود این مطلب ، برای آموزش جوانان هنوز از همان روشی استفاده می شود که سقراط و افلاطون ، حقایق عالی اخلاقی را برای شیفتگان منطق و فلسفه و برای علاقمندان سخنوری و علم کلام بیان می کردند . در حقیقت در درسهای حساب ، هندسه و جبر ،هرگز لزوم یادگیری آنها برای زندگی عملی خاطر نشان نمی شود. هرگز از تاریخ علم صحبتی به میان نمی آید. نظریه های سنگین علمی ، ولی هیچ نتیجه ای جز این ندارد که دانش آموزان را از علم بری کند و عدّه ی آنها را تقلیل دهد . یکی ازراههای جدی برای حلّ مسئله توجه به تاریخ علم، گفتگو در باره ی مردان علم و ارتباط ریاضی با عمل است ، ارتباطی که در تمام دوران زندگی بشر هرگز قطع نشده است . ● کاربرد ارقام در زمانهای قدیم هر قدمی که در راه پیشرفت تمدّن برداشته می-شد، بر لزوم استفاده از اعداد می افزود . اگر شخصی گله ای از گوسفندان داشت ، می خواست آن را بشمرد ،یا اگر می خواست معبد یا هرمی بسازد ، باید می دانست که چقدر سنگ برای آن لازم دارد . اگر دارای زمین بود ، می خواست آن رااندازه گیری کند . اگر قایقش را به دریا می راند ، می خواست فاصله ی خود را از ساحل بداند . و بالاخره در تجارت و مبادله ی اجناس در بازارها ، باید ارزش اجناس حساب می شد.هنگامی که آدمی محاسبه با ارقام را آموخت ، توانست زمان ، فاصله مساحت ، حجم را اندازه گیری کند . با بکار بردن ارقام ، انسان بردانش و تسلّط ...
اطلس ریاضی: کاربردهای ریاضیات در علوم
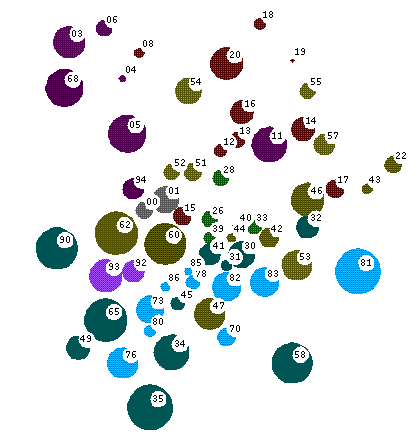
اطلس ریاضی: کاربردهای ریاضیات در علوم ترجمه: ابوالفضل گروئی - منبع: سایتwww.math.niu.edu * در صورت تمایل میتوانید اصل مقاله را در انتها مطالعه فرمائید. از نظر تاریخی، این نیازهای علوم فیزیکی بوده است که محرک توسعه بسیاری از قسمتهای ریاضیات، به ویژه آنالیز بوده اند. گاهی اوقات مشکل است که کاربردها را از نظر ریاضی طبقه بندی کرد، چرا که ابزارهائی از چند حوزه ریاضیات ممکن است به کار گرفته شده باشند. ما روی این کاربردها نه فقط با بحث درباره طبیعت نظم (و سازماندهی) آنها متمرکز میشویم، بلکه برهمکنش آنها با ریاضیات را نیز مد نظر قرار میدهیم. بیشتر حوزه ها در این گروه (نقاط آبی در تصویر) در مجموع با عنوان «فیزیک ریاضی» شناخته شده اند. تا اندازه ای، ابزارهای ریاضی جدیدتر و به طور پیشرونده پیچیده تر در مهندسی، زیست شناسی و علوم اجتماعی (نواحی بنفش در تصویر) به کار گرفته میشوند. 70- مکانیک ذرات و سیستمها: مطالعه دینامیک مجموعه های ذرات یا توده های جامد (تو پر)، شامل توده های چرخان یا لرزان. از اصول تغییرات (انرژی-کمینه سازی) همچنین معادلات دیفرانسیل استفاده میکند. Equilibrium in statistical mechanics: systems exchanging energy are most likely to have individual energies that maximize the overall number of states. (Image by Prof. Mehran Kardar.) تعادل در مکانیک آماری: سیستمهای مبادله کننده انرژی تمایل به داشتن انرژیهای مشخصی دارند که تعداد کل حالتها را بیشینه میکند (تصویر از پروفسور مهران کاردار از سایت: www.core.org.cn) 74- مکانیک توده های تغییر شکل پذیر: معادلات الاستیسیته و پلاستیسیته، انتشار موج، مهندسی و حوزه هائی در جامدات ویژه مانند خاکها و بلورها را در نظر میگیرد. مثالهای تغییر شکل کره: الف) شکل ابتدائی ب) کشش و پ) نیشگون گیری. 76- مکانیک سیالات: هوا، آب و دیگر سیالات در حال حرکت را بررسی میکند؛ همچنین: تراکم، اغتشاش، نفوذ، انتشار موج و غیره. از نظر ریاضی، مطالعه حلهای معادلات دیفرانسیل شامل روشهای عددی در مقیاس بالا (برای نمونه، روش اجزای محدود) را در بر میگیرد. Image by Bomphrey et al. (Phy. of Fluid 2002) بررسی رفتار سیال (هوا) در اطراف یک ملخ چرخان. تصویر از بامفری و همکاران (در مجله فیزیک سیال ۲۰۰۲). 78- نورشناخت (اپتیک)، تئوری الکترومغناطیس: بررسی انتشار و تغییر شکل امواج الکترومغناطیسی شامل مباحث تداخل و پراش است. در کنار شاخه های متداول آنالیز، این حوزه مباحث هندسی مانند مسیرهای پرتوهای نوری را نیز در بر میگیرد. انتهای رشته(فیبر)های نوری. 80- ترمودینامیک کلاسیک، انتقال گرما: بررسی شارش گرما از میان ماده شامل تغییر فاز و احتراق است. از نظر تاریخی منشاء سریهای «فوریه» است. نیمرخ (پروفایل) توزیع دما در لوله آب خنک ...
کاربرد ریاضی در زندگی
دراین مقاله سعی شده است که ارتباط دروس کتب ریاضی راهنمایی با سایر علوم و همچنین کاربرد آنها در دنیای امروز ی تا حدودی بررسی شود و ارائه گردد . بین رشته های علمی ، که بشر در طول هزاران سال به وجود آورده ، ریاضیّات جای مخصوص و ضمناٌ مهمّی را اشغال کرده است . ریاضیّات با علوم فیزیک ، زیست شناسی ، اقتصاد و فنون مختلف فرق دارد . با وجود این به عنوان یکی از روشهای اصلی در بررسیهای مربوط به کامپیوتر ، فیزیک ، زیست شناسی ، صنعت واقتصاد بکار می رود ودرآینده بازهم نقش ریاضّیات گسترش بیشتری می یابد. با وجود این مطلب ، برای آموزش جوانان هنوز از همان روشی استفاده می شود که سقراط و افلاطون ، حقایق عالی اخلاقی را برای شیفتگان منطق و فلسفه و برای علاقمندان سخنوری و علم کلام بیان می کردند . در حقیقت در درسهای حساب ، هندسه و جبر ،هرگز لزوم یادگیری آنها برای زندگی عملی خاطر نشان نمی شود. هرگز از تاریخ علم صحبتی به میان نمی آید. نظریه های سنگین علمی ، ولی هیچ نتیجه ای جز این ندارد که دانش آموزان را از علم بری کند و عدّه ی آنها را تقلیل دهد . یکی ازراههای جدی برای حلّ مسئله توجه به تاریخ علم، گفتگو در باره ی مردان علم و ارتباط ریاضی با عمل است ، ارتباطی که در تمام دوران زندگی بشر هرگز قطع نشده است . ● کاربرد ارقام در زمانهای قدیم هر قدمی که در راه پیشرفت تمدّن برداشته می شد، بر لزوم استفاده از اعداد می افزود . اگر شخصی گله ای از گوسفندان داشت ، می خواست آن را بشمرد ،یا اگر می خواست معبد یا هرمی بسازد ، باید می دانست که چقدر سنگ برای آن لازم دارد . اگر دارای زمین بود ، می خواست آن رااندازه گیری کند . اگر قایقش را به دریا می راند ، می خواست فاصله ی خود را از ساحل بداند . و بالاخره در تجارت و مبادله ی اجناس در بازارها ، باید ارزش اجناس حساب می شد.هنگامی که آدمی محاسبه با ارقام را آموخت ، توانست زمان ، فاصله مساحت ، حجم را اندازه گیری کند . با بکار بردن ارقام ، انسان بردانش و تسلّط خود بر دنیای پیرامونش افزود . ● کاربرد توابع و روابط بین اعداد کاربرد روابط بین اعداد و توابع و نتیجه گیریهای منطقی در نوشتن الگوریتمها و برنامه نویسی کامپیوتری است . مفهوم تابع یکی از مهمترین مفاهیم ریاضی است و در اصل تابع نوعی خاص از رابطه های بین دو مجموعه است . و با توجه به این که دنباله ها هم حالت خاصی از تابع است – تابعی که دامنه آن مجموعه ی اعداد { . . . و ۲ و ۱ و ۰ } است – دنباله های عددی در ریاضی و کامپیوتر کاربرد فراوان دارند . برای ساخت یک برنامه اساساٌ چهار مرحله را طی می کنیم : ۱) تعریف مسئله ۲) طراحی حل ۳) نوشتن برنامه ۴) اجرای برنامه لازم به ذکر است ...
