نظریه گراف و کاربردهای آن
دانلود رایگان نظریه گراف و کاربردهای آن
دانلود رایگان نظریه گراف و کاربردهای آن
نمونه سوالات درس « نظریه گراف و کاربردهای آن »+همراه پاسخنامه
این پیج به دلایلی مسدود شده است
نمونه سوال نظریه گراف و کاربردهای آن پیام نور کلیه گرایش ها 91-90

نمونه سوال نظریه گراف و کاربردهای آن پیام نور کلیه گرایش ها 91-90 دانلود
نظریه گراف
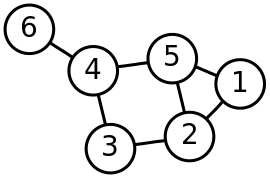
نظریه گراف نظریه گراف شاخهای از ریاضیات است که دربارهٔ گراف ها بحث میکند. به صورت شهودی، گراف نموداری است، شامل تعدادی رأس، که با یالهایی به هم وصل شدهاند. فهرست مندرجات ۱ تعریف ۲ انواع گراف ۳ خصوصیات گرافهای خاص ۴ مطالعهٔ بیشتر تعریف تعریف دقیقتر گراف به این صورت است، که گراف مجموعهای از رأسها است، که توسط خانوادهای از زوجهای مرتب که همان یالها هستند به هم مربوط شدهاند. یالها بر دو نوع ساده و جهت دار هستند، که هر کدام در جای خود کاربردهای بسیاری دارد. مثلاً اگر صرفاً اتصال دو نقطه -مانند اتصال تهران و زنجان با کمک آزادراه- مد نظر شما باشد، کافیست آن دو شهر را با دو نقطه نمایش داده، و اتوبان مزبور را با یالی ساده نمایش دهید. اما اگر بین دو شهر جادهای یکطرفه وجود داشته باشد آنگاه لازمست تا شما با قرار دادن یالی جهت دار مسیر حرکت را در آن جاده مشخص کنید. آغاز نظریهٔ گراف به سدهٔ هجدهم بر میگردد. اولر ریاضیدان بزرگ مفهوم گراف را برای حل مسئله پلهای کونیگسبرگ ابداع کرد اما رشد و پویایی این نظریه عمدتاً مربوط به نیم سدهٔ اخیر و با رشد علم انفورماتیک بودهاست. مهمترین کاربرد گراف مدلسازی پدیدههای گوناگون و بررسی بر روی آنهاست. با گراف میتوان به راحتی یک نقشه بسیار بزرگ یا شبکهای عظیم را در درون یک ماتریس به نام ماتریس وقوع گراف ذخیره کرد و یا الگوریتمهای مناسب مانند الگوریتم دایسترا یا الگوریتم کروسکال و ... را بر روی آن اعمال نمود. یکی از قسمتهای پرکاربرد نظریهٔ گراف، گراف مسطح یا هامنی است که به بررسی گرافهایی میپردازد که میتوان آنها را به نحوی روی صفحه کشید که یالها جز در محل راسها یکدیگر را قطع نکنند. این نوع گراف در ساخت جادهها و حل مساله کلاسیک و قدیمی سه خانه و سه چاه آب به کار میرود. نظریه گراف یکی از پرکاربردترین نظریهها در شاخههای مختلف علوم مهندسی (مانند عمران)، باستانشناسی (کشف محدوده یک تمدن) و ... است. روابط میان راس های یک گراف را می توان با کمک ماتریس بیان کرد . انواع گراف گراف ساده: هر گراف G زوج مرتبی مانند (V,E) است که در آن V مجموعهای متناهی و ناتهی است و E زیرمجموعهای از تمام زیرمجموعههای دو عضوی V میباشد. اعضای V را رأسهای G و اعضای E را یالهای G مینامیم. به بیان ساده تر بین دو رأس یک گراف ساده حداکثر یک یال وجود دارد. گراف چندگانه: هرگاه بین دو رأس متمایز از یک گراف بیش از یک یال وجود داشته باشد، آن را یک گراف چند گانه میگوییم. گراف جهت دار: هر گراف G زوج مرتبی مانند (V,E) است که در آن V مجموعهای متناهی و ناتهی است و E زیرمجموعهای ...
نمونه سوال نظريه گراف و كاربردهاي آن
به درخواست دوستان دو نمونه سوال از درس "نظريه گراف و كاربردهاي آن" رو روي وبلاگ قرار دادم و اميدوارم كه مورد استفاده شما قرار بگيره:
تاریخچه نظریه گرافها
مقدمه:اندک زمانی است که واژه گراف در ادبیات ریاضی وارد شده است، گرچه شروع آن را می توان از زمان لئناردو اویلر ریاضیدان سوئیسی (1707-1783) دانست. اما علاقه ی شدید و مداوم به نظریه ی گراف ، بعنوان شاخه ای از ریاضیات ، از سال 1930 به بعد، آشکار گردید و امروزه این نظریه یکی از پربارترین و محبوب ترین شاخه های ریاضیات و علوم کامپیوتر است و علت آن نیز به خاطر قابلیت کاربرد آن در بسیاری از مسائل گسترده ی جامعه مدرن امروزی است.هنگامی که مساله ای به زبان گراف فرمول بندی شد، درک آن بسیار آسان تر خواهد شد. امروزه نظریه ی گراف یکی از موضوعات مهم دئر ریاضیات گسسته است. گرافها، مدل های راضی برای یک مجموعه گسسته هستند، که اعضای آن به طریقی با هم مرتبط می باشند. اعضای این مجموعه می توانند انسان ها یا رابطه ی خویشاوندی ، یا دوستی و… باشد. اعضای این مجوعه می توانند، محل اتصالهای سیم های یک شبکه ی برق و رابطه ی آنها، سیم های واصل بین دو مقطه باشد و یا عناصر مجوعه می توانند اتم های یک مولکول و ارتباط آن ها، اتصالهای شیمیایی باشد. نظریه گراف ریشه در بازیها و معما ها نیز دارد، اما امروزه این نظریه نه تنها در ریاضیات بلکه در سایر علوم مانندا اقتصاد، روانشناسی،ژنتیک و باستان شناسی کاربرد فراوانی دارد.مفهوم گراف:واژه گراف، نه تنها در ریاضیات، بلکه در سایر علوم و حتی در زندگی روزانه به نام های گوناگون مانند طرح دیاگرام، نگاره، نقشه، ماز و… بکار می رود. مثلا ممکن است به بهانه های مختلف شکلی رسم کنیم که از نقطه هایی تشکیل شده باشد و اگر چند نقطه، رابطه هایی با هم داشته باشند این روابط را با کشیدن خط بین آن ها نشان دهیم. نیز می توانیم تیم های ورزشی را در نظر بگیریم و آن ها را با نقاط A,B,C,… روی صفحه رسم کنیم و خطوط را با این شرط وصل کنیم که آن تیم ها با هم بازی داشته باشند، در ابتدا که بازی صورت نگرفته فقط چند نقطه داریم، ولی وقتی تیم ها باهم بازی کردند، بین تمام نقاط خط هایی وصل کنیم، بدین ترتیب یک گراف ساخته ایم، که با یک نگاه، راحت متوجه رابطه بین نقاط می شویم. بدیهی است که در انتخاب مکان نقاط در صفحه و طرز رسم کردن خطوط آزاد بوده ایم. اگر هیچ تیمی بازی نکرده باشد، هیچ خطی وصل نمی شود و در این صورت گراف، گراف صفحه نخواهد بود و اگر با هم بازی کنند، گراف کامل بوجود می آید.قابل ذکر است که اگر نقاط را رئوس گراف و خطوط را یال بنامیم داریم: G(V.E) که آن را گراف G با رئوس V. و یال های E می نامیم.اکنون به معرفی چند نوع گراف می پردازیم:1) گراف های یکریخت: اگر در دو گراف، تعداد راس ها برابر بوده، بطوریکه هر دو راس متناظر، با یک حرف نام گذاری شده باشد، آن گاه وقتی ...
کاربرد نظریه گراف
از گرافها برای حل مسایل زیادی در ریاضیات و علوم کامپیوتر استفاده میشود. ساختارهای زیادی را میتوان به کمک گرافها به نمایش در آورد. برای مثال برای نمایش چگونگی رابطه وب سایتها به یکدیگر میتوان از گراف جهت دار استفاده کرد. به این صورت که هر وب سایت را به یک راس در گراف تبدیل میکنیم و در صورتیکه در این وب سایت لینکی به وب سایت دیگری بود، یک یال جهت دار از این راس به راسی که وب سایت دیگر را نمایش میدهد وصل میکنیم. از گرافها همچنین در شبکهها، طراحی مدارهای الکتریکی، اصلاح هندسی خیابانها برای حل مشکل ترافیک، و.... استفاده میشود. مهمترین کاربرد گراف مدلسازی پدیدههای گوناگون و بررسی بر روی آنهاست. با گراف میتوان به راحتی یک نقشه بسیار بزرگ یا شبکهای عظیم را در درون یک ماتریس به نام ماتریس وقوع گراف ذخیره کرد و یا الگوریتمهای مناسب مانند الگوریتم دایسترا یا الگوریتم کروسکال و ... را بر روی آن اعمال نمود. در این جا به بررسی گرافهایی میپردازد که میتوان آنها را به نحوی روی صفحه کشید که یالها جز در محل راسها یکدیگر را قطع نکنند. این نوع گراف در ساخت جادهها و حل مساله کلاسیک و قدیمی سه خانه و سه چاه آب به کار میرود. کاربرد گراف بازهها از گرافها برای حل مسایل زیادی در ریاضیات و علوم کامپیوتر استفاده میشود. ساختارهای زیادی را میتوان به کمک گرافها به نمایش در آورد. درخت و ماتریس درخت در رشتههای مختلفی مانند شیمی مهندسی برق و علم محاسبه کاربرد دارد . کیرشهف در سال ۱۸۴۷ میلادی هنگام حل دستگاههای معادلات خطی مربوط به شبکههای الکتریکی درختها را کشف و نظریه درختها را بارور کرد. کیلی در سال ۱۸۵۷ میلادی درختها را در ارتباط با شمارش ایزومرهای مختلف هیدروکربنها کشف کرد وقتی مثلا میگوییم در ایزومر مختلف c4h۱۰ وجود دارد منظورمان این است که دو درخت متفاوت با ۱۴ راس وجود دارند که درجه ۴ راس از این ۱۴ راس جهار و درجه هر یک از ۱۰ راس باقیمانده یک است. اگر هزینه کشیدن مثلا راه آهن بین هر دو شهر ازp شهر مفروض مشخص باشد ارزانترین شبکه ای که این p شهر را به هم وصل میکند با مفهوم یک درخت از مرتبه p ارتباط نزدیک دارد. به جای مساله مربوط به راه آهن میتوان وضعیت مربوط به شبکههای برق رسانی و لوله کشی نفت و لوکشی گاز و ایجاد کانالهای آبرسانی را در نظر گرفت . برای تعیین یک شبکه با نازلترین هزینه از قاعده ای به نام الگوریتم صرفه جویی استفاده میشود که کاربردهای فراوان دارد. از گرافها می توان به عنوان کدهای کمکی نام برد که به DVB Playerها در بالا بردن قابلیتهای آنها کمک میکنند. گرافها دارایی مزایای ...
بارم بندی جدید ریاضیات گسسته چهارم ریاضی
توجه: این بارم بندی هنوز از سوی اداره کل سنجش و ارزشیابی تایید نشده ولی قابل اعتماد است.پایانی اولنمرهپایانی دومنمرهفصل1: گراف ها و کاربردهای آن9فصل1: گراف ها و کاربردهای آن2فصل2: نظریه اعداد11فصل2: نظریه اعداد3فصل3: مباحثی دیگر در ترکیبیات7فصل 4: احتمال8جمع20جمع20
روش مطالعه گسسته
درس ریاضیات گسسته یکی از سه درس ریاضی سال چهارم است که با 10 الی 14 سؤال در کنکور سراسری، نقش مهمی در تعیین سرنوشت دانشآموزان دارد. (البته با توجه به 2 یا 3 سؤالی که از پایههای این درس یعنی جبر و احتمال مطرح میشود، معمولاً حدود 13 یا 14 سؤال از این مفاهیم در کنکور وجود دارد .) محتوای درس: در این درس، چهار فصل مختلف مورد بررسی قرار گرفته است: فصل اول: گراف و کاربردهای آندر این فصل، مطالب زیر مورد بررسی قرار گرفته است: - معرفی و کاربردها: ابتدا به معرفی و تعاریف بحث گراف پرداخته شده و چند گراف کاربردی مانند گراف مشاغل و گراف بازهها معرفی شدهاند. در این قسمت باید بتوانید تعداد گرافهای قابل تولید را در حالات مختلف به دست آورید. همچنین شمارش حالات توزیع مشاغل بین داوطلبان و تشخیص اینکه گرافی، گراف بازهها هست یا نه، از مطالب این قسمت است . - مفاهیم (مرتبه، اندازه، درجه، مسیر، دور): در قسمت بعدی مفاهیم اصلی گراف و تعاریف مرتبط به بحث گراف مانند مسیر و دور معرفی شدهاند. نامساویهای موجود بین مرتبه و اندازه و ماکزیمم و مینیمم درجات رئوس، رابطهی بین مجموع درجات رئوس با تعداد یالها، شمارش تعداد مسیرها و دورها خصوصاً در گراف کامل از مطالب اصلی این قسمت است. همچنین تعاریف مرتبط به مسیر و دور مانند همبندی، بخشهای جدا از هم، فاصله، گراف همیلتنی و گراف اویلری از دیگر مطالبی است که اکثراً در قسمت تمرینات کتاب مورد توجه قرار گرفته است. - درخت: یکی از مهمترین گرافها به علت اینکه مرز دقیق همبندی و ناهمبندی را مشخص میکند و معرف گرافی که با حداقل یالها همبند است، درخت است. باید نکات و قضایای مهم درخت که در کتاب و تمرینات مطرح شده (مانند حداقل تعداد رأسهای درجه یک و رابطهی بین یالها و رئوس) را به خوبی بشناسید. - گراف و ماتریس: در پایان این فصل برای بیان منظم و تسهیل در معرفی و استفاده از گراف نمایشی ماتریسی از گراف ارائه شده است و انتظار می رود دانشآموز پس از سپری کردن این قسمت، تمام مطالبی که در قسمتهای قبلی آموخته است را بتواند به صورت ماتریسی شبیهسازی کند . فصل دوم : نظریه اعداد در این فصل، مطالب زیر مورد بررسی قرار گرفته است: - استقرا و خوشترتیبی: دو اصل استقرای ریاضی و خوشترتیبی و کاربردهایشان معرفی شدهاند. - تقسیمپذیری: در این قسمت به تعریف تقسیمپذیری و ویژگیهای مهم آن پرداخته میشود. باید بتوانید تعیین کنید یک چندجملهای چه هنگامی بر یک چندجملهای دیگر تقسیمپذیر است. - الگوریتم تقسیم: حالت کلی قضیهی تقسیم و کاربردهای آن در پیدا کردن باقیمانده و خارج قسمت تقسیم در ...
لیست جدید ارائه دروس مهندسی فناوری اطلاعات(طرح تجمیع)
سلامدانشگاه پیام نور مجددا لیست دروسی که باید گذراند را تغییر داد البته این بار بیشتر توجه آنها به رعایت پیش نیازها بوده است. شما می توانید این تغییرات را در قسمت زیر مشاهده کرده و یا در صورت تمایل لیست جدید را از اینجا دانلود کنید. تغییراتی که این لیست نسبت به لیست ارائه شده ترم گذشته دارد:اضافه شدن درس نظریه گراف و کاربردهای آن به دروس اختیاری (پیش نیاز: ساختمان گسسته)تغییر پیش نیاز درس سیستم های اطلاعات مدیریت (قبل: گذراندن 140واحد درسی. جدید: مهندسی نرم افزار1)تغییر پیش نیاز کارآموزی و پروژه (قبل: نیاز به گذراندن 130واحد و شیوه ارائه مطالب. جدید: نیاز به گذراندن درسهای شیوه ارائه مطالب، مهندسی فناوری اطلاعات1، شبکه کامپیوتری2، مهندسی نرم افزار۲)موفق باشید
