نسبت های مثلثاتی
نسبت های مثلثاتی
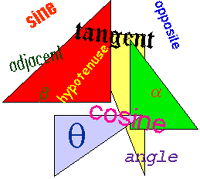
مطالعه روی زوایا و روابط موجود میان زوایای اشکال مسطح و سه بعدی مثلثات نامیده میشود.تابع مثلثاتی از قبیل سینوس و کسینوس توابعی هستند که بوسیله روابط هندسی تعریف میشوند.تاریخچه اولین کسانی که از مثلثات استفاده میکردند یونانیان بودند.در یونان قدیم از مثلثات برای تعیین طول مدت روز یا طول سال (با مشخص کردن موقعیت ستارگان در آسمان)استفاده میشد.بعدها ریاضیدانان و منجمان هندی نیز پیشرفتهایی در مثلثات بدست آوردند ولی پیشرفت این علم مدیون دانشمندان مسلمان است .مسلمانان اصلیترین نقش را در پیشرفت این علم ایفا کردند و سپس این اندوختهها را در قرون وسطی به اروپاییان منتقل کردند. اروپاییان نیز دانش فراوان مسلمانان در مثلثات استفاده کردند و این علم را توسعه داده و به شکل امروزی در آوردند.کاربردها علم مثلثات در نجوم کاربرد فراوانی دارد و ازآن برای اندازهگیری فواصل بین ستارگان استفاده میشود. همچنین در طراحی سیستمهای ماهواره ای از مثلثات استفاده فراوانی میشود.در دریانوردی نیز از مثلثات برای تشخیص جهتهای جغرافیایی کمک گرفته میشود.امروزه از مثلثات در شاخه های مختلف فیزیک ماننداپتیک ، اکوستیک ، در تحلیل بازارهای مالی، الکترونیک ، معماری ، اقیانوس شناسی ، مکانیک ، بلور شناسی ، ژئودزی ، عمران و اقتصاد استفاده فراوانی میشوددایره مثلثاتیدر ریاضیات دایره مثلثاتی دایرهای به شعاع واحد است. x و y دو مختصه روی این دایره هستند که بنا به تعریف دایره:x2 + y2 = 1نقطه (x, y) روی این دایره با (۰, ۰) زاویهای میسازد که از روابط زیر بدست میآید:دایره مثلثاتی با نمایش زاویه t در نقطه (x, y)بنابر این خواهیم داشت:و از آنجا که توابع سینوس و کسینوس دورهای (پریودیک) هستند:که در آن k عددی صحیح است. سایر توابع مثلثاتی نظیر تانژانت و کتانژانت و سکانت و کسکانت را میتوان به همین ترتیب بدست آورد.فرمولهای مهم مثلثاتفرمول های مهم مثلثات برای تبدیل و محاسبهـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــ(فرمول طلایی)ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــ(تبدیل ضرب به جمع)ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ...
مثلثات(1)
نسبت های مثلثاتی:سینوس یکی از نسبتهای مثلثاتی است.تعریف درمثلث قائمالزاویه نسبت ضلع مقابلهر زاویه حاده به وتر را سینوس آن زاویه مینامند. سینوس را در متنهای عربی و فارسی قدیم «جیب» مینامیدند. تابع سینوس:تابع سینوس تابعی است که مقدار کمان (زاویه) را به عنوان متغیر میپذیرد و اندازه سینوس زاویه را به ما میدهد. دامنه این تابع تمام اعداد حقیقی بوده و برد آن بازه [1,1 − ] است. شکل تابع f(x) = sinx گویاست که این تابع متناوب و فرد بوده و دوره تناوب آن 2π میباشد. کسینوس:کسینوس یکی از نسبتهای مثلثاتی است. اصطلاح قدیمی این نسبت در ریاضیات و اخترشناسی قدیم جیب تمام بودهاست. تعریف:در مثلث قائمالزاویه نسبت ضلع مجاور هر زاویه حاده به وتر را کسینوس آن زاویه مینامند. تابع کسینوس:تابع کسینوس تابعی است که مقدار کمان (زاویه) را به عنوان متغیر میپذیرد و اندازه کسینوس زاویه را به ما میدهد. دامنه این تابع تمام اعداد حقیقی بوده و برد آن بازه [1,1 − ] است. شکل تابع f(x) = cosx گویاست که این تابع متناوب بوده و دوره تناوب آن 2π میباشد. تابع کسینوس تابعی زوج میباشد.
توابع مثلثاتی
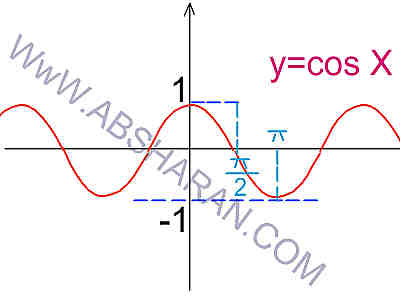
تابع مثلثاتی Cos نیز یکی از توابع مهم مثلثاتی است.همانطور که از نمودارد تابع مثلثاتی Cos پیداست,این تابع یک تابع زوج است (نسبت به محور Y قرینه است).دامنه ی تابع مثلثاتی Cos مجوعه ی اعداد حقیقی و برد این تابع مثلثاتی اعداد بین 1 و 1- می باشند.یعنی مقدار از 1 بیشتر و از 1- کمتر نمی شود.نمودار تابع Cos بصورت زیر است: با توجه به نمودار تابع مثلثاتی Cos این تابع نیز یک به یک نمی باشد.از آنجاییکه تابع Cos یک تابع زوج است پس رابطه ی زیر برقرار می باشد: آموزش مثلثات,تابع مثلثاتی سینوس Sin یکی از توابع پرکاربرد مثلثاتی است.همانطور که از نمودار تابع مثلثاتی سینوس پیداست,این تابع یک تابع فرد است (نسبت به مبداء مختصات قرینه است).دامنه ی تابع مثلثاتی سینوس sin مجوعه ی اعداد حقیقی و برد این تابع مثلثاتی اعداد بین 1 و 1- می باشند.یعنی مقدار سینوس از 1 بیشتر و از 1- کمتر نمی شود.نمودار تابع Sin سینوس بصورت زیر است: با توجه به نمودار تابع مثلثاتی سینوس Sin این تابع یک به یک نیز نمی باشد.از آنجاییکه تابع سینوس یک تابع فرد است پس رابطه ی زیر برقرار می باشد: Y=Sin(-X)=-SinX آموزش مثلثاتدر ابتدای آموزش مثلثات به بررسی دایره ی مثلثاتی می پردازیم,دایره ی مثلثاتی شما را در یافتن مقادیر زاویه ها در مثلثات یاری می کند.: هر دایره دارای یک مبداء بوده که شروع حرکت متحرک از آن جا آغاز می گردد,دارای 4 ناحیه می باشد,دارای جهت اصلی خلاف عقربه های ساعت (جهت مثبت) می باشد.دارای 4 محور است که محور سینوس Sin و تانژانت tg موازی هم و محور Cos و کتانژانت Cotg در دایره ی مثلثاتی موازی هم هستند. تغییرات sin و cos بین 1 و 1- و تغییرات تانژانت tg و cotg از تا است. روش محاسبه ی نسبت های مثلثاتی: برای محاسبه ی sin و cos یک زاویه انتهای کمان را بر محور Sin و یا cos عمود می کنیم,ولی برای محاسبه ی tg و یا cotg یک زاویه انتهای کمان را امتداد داده تا محور tg و یا cotg را قطع کند. اگر x زاویه ای در ناحیه ی اول باشد,در ناحیه ی اول تمام نسبت های مثلثاتی مثبت است. اگر x در ناحیه ی دوم باشد فقط سینوس sin مثبت است. اگر x در ناحیه ی سوم باشد در ناحیه ی سوم سینوس sin و cos منفی و تانژانت tg و کتانژانت cotg مثبت است. اگر x در ناحیه ی چهارم باشد,در ناحیه ی چهارم فقط cos مثبت است. ده رابطه ی مهم مثلثاتی: ================================================================================================ نسبت های مثلثاتی کمان 2x : ============================================================================= نسبت های مثلثاتی زوایای 3x : ================================================================================================= نکته: ==================================================================================================== چند نسبت دیگر: ================================================================================================== فرمول ...
جدول نسبتهای مثلثاتی برای زوایای 0 تا 90 درجه
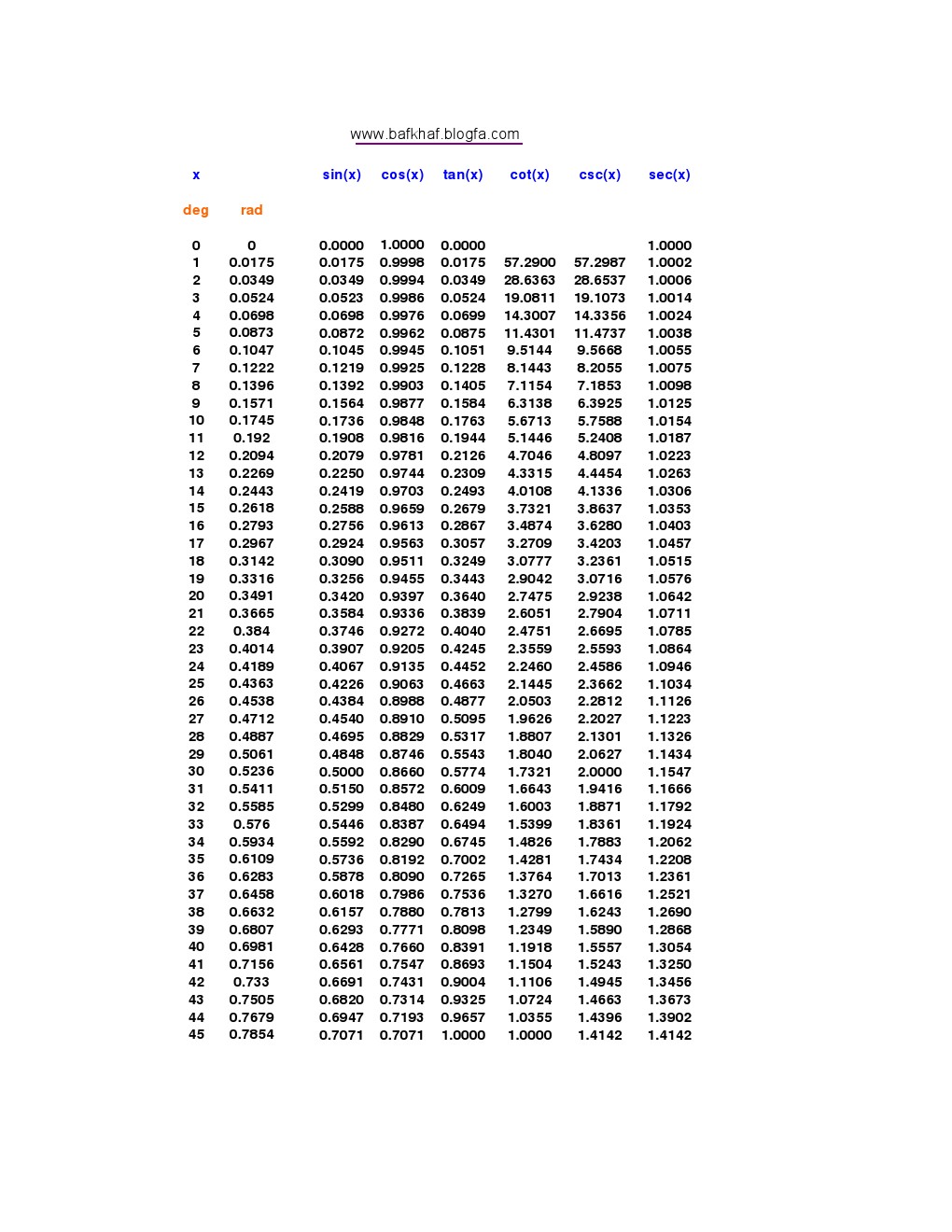
این عکسها قابلیت زوم بالایی دارند تا در موبایل و کامپیوتر استفاده شوند. همچنین میتوان از آنها پرینت گرفت.
فرمول ها و نسبت های مثلثاتی

فرمولهای کاربردی مثلثات و جزوه ی نسبت های مثلثاتی دانش آموزان عزیز و داوطلبان کنکور می توانند در این پست دو فایل مربوط به مثلثات را دانلود نمایند. فایل اول شامل فرمول ها و روابط کاربردی مثلثات دوره دبیرستان می باشد. در فایل دوم درسنامه ای جامع مربوط به نسبت های مثلثاتی شامل مباحثی چون واحد های اندازه گیری زاویه – دایره مثلثاتی – روابط بین نسبت های مثلثاتی و… همراه با ارائه ی مثال ها و تست های مختلف از این مبحث ارائه شده است. این جزوات توسط مهندس دانیال ظفری کارشناس ارشد مهندسی هوا فضا از دانشگاه شریف، تهیه و به سایت ریاضی سرا ارسال گردیده است.. با تشکر از استاد ظفری دانلود فرمول های مثلثاتی فرمت فایل : pdf حجم فایل : ۳۰۰ کیلوبایت پسورد فایل: www.riazisara.ir دانلود درسنامه ی نسبت های مثلثاتی فرمت فایل : pdf حجم فایل : ۸۹۰ کیلوبایت پسورد فایل: www.riazisara.ir
روش محاسبه ی نسبت های مثلثاتی:
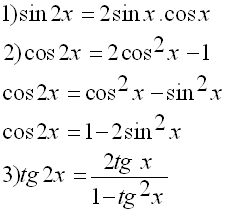
نسبت های مثلثاتی کمان 2x : نسبت های مثلثاتی زوایای3x : نکته:چند نسبت دیگر:فرمول های سینوس sin و cos بر حسب تانژانت نصف کمان:زوایای قرینه:زوایای ():زوایای ():نکته:هرگاه بخواهیم مضارب فرد عدد را از کمان سینوس sin یا cos حذف کنیم,باید یک منفی در پشت نسبت مثلثاتی ضرب کنیم.ولی اگر مضارب فرد عدد را از کمان تانژانت و یا کتانژانت حذف کنیم نیاز به ضرب منفی در پشت نسبت مثلثاتی نیست.همچنین اگر بخواهیم مضارب زوج عدد را از کمان تمام نسبت های مثلثاتی حذف کنیم,نیاز به ضرب منفی در پشت نسبت های مثلثاتی نیست. نکته ها: فرمول های بسط نسبت های مثلثاتی:تبدیل جمع به ضرب:تبدیل ضرب به جمع: Arc ها:Arc به معنی کوچکترین زائیه یا کمان می باشد,مثلا یعنی کوچکترین زاویه ای که sin آن است که می شود نکته: هرگاه در Arc ها با مقادیر منفی رو به رو شویم,در مورد سینوس arc sin و arc tg ابتدا منفی را نادیده گرفته سپس کمان را یافته و منفی را به کمان می دهیم.اما در مورد arc cos و arc cot ابتدا منفی را نادیده گرفته سپس کمان را یافته و آن را از کم می کنیم. نکاتی در مورد arc ها: منبع:http://kashan-math.blogfa.com
