معادله گرما
معادله گرما
گرما در فیزیک، انتقال انرژی گرمایی بین مرز مشخص دو سیستم ترمودینامیکی است. این ویژگی دینامیک است و به صورت ایستا در ماده موجود نیست. در این زمینه گرما به عنوان مترادف انرژی گرمایی به کار گرفته شدهاست. روش بنیادی در انتقال گرما در مهندسی شامل رسانش، همرفت و تابش است. قوانین فیزیکی رفتار و خصوصیات هر کدام از روشها را شرح میدهند. سیستم واقعی اغلب ترکیب پیچیدهای از آنها را نشان میدهد. روشهای انتقال گرما در رشتههای متعدد مورد استفاده قرار میگیرند: مانند مهندسی خودرو، مدیریت گرمایی وسایل الکترونیکی و سیستمها، کنترل آب و هوا، عایق و پردازش مواد. روشهای متنوع مکانیکی برای تحلیل وتخمین نتایج انتقال گرما در سیستمها گسترش پیدا کردهاند. انتقال گرما یک تابع مسیر (یا فرایند مقدار) است که به حالت ماده بستگی ندارد. بنابراین مقدار انتقال گرما در فرایند ترمودینامیکی که حالت سیستم تغییر میکند، نه فقط به اختلاف خالص بین ابتدا و انتهای فرایند، بلکه بستگی به این دارد که فرایند چگونه اتفاق میافتد. شار گرما نماینده مقدار و بردار جریان گرما در یک سطح است. انتقال گرما به طور معمول به عنوان بخشی از برنامه درسی مهندسی شیمی و مهندسی مکانیک مورد مطالعه قرار میگیرد. به طور معمول، ترمودینامیک پیش نیاز دورههای آموزشی انتقال گرما است مانند مواقعی که قوانین ترمودینامیکی اصول مکانیزم انتقال گرما هستند. سایر آموزشهای وابسته به انتقال گرما شامل تبدیل انرژی و انتقال جرم هستند. معادلات انتقال انرژی گرمایی (قوانین فوریه)، حرکت مکانیکی (قوانین نیوتون برای سیالات) و انتقال جرم (قوانین نفوذ فیک) مشابه هستند و آنالوژی بین این سه فرایند انتقال، برای تسهیل پیش بینی هر یک از آنها به بقیه آنها گسترش پیدا کردهاست. شیوههای بنیادی انتقال گرما عبارتند از: رسانش یا نفوذ: انتقال انرژی بین اجسام که در تماس فیزیکی هستند.همرفتی: انتقال انرژی بین یک جسم و محیط اطراف به دلیل حرکت سیال.تابش: انتقال انرژی به/از جسم به وسیله تابش یا جذب پرتوهای الکترومغناطیسی.انتقال جرم: انتقال انرژی از یک مکان به مکان دیگربه عنوان اثر جانبی انتقال فیزیکی جسم حاوی انرژی.رسانش در مقیاس میکروسکوپیک، رسانش گرمایی در اتمها و مولکولهای در حال ارتعاش و برخورد و برهمکنش آنها با مولکولها و اتمهای مجاور یا حرکت تند و داغ اتمها صورت میگیرد که بخشی از انرژی خود (گرما) را به ذرات همسایه منتقل میکنند. به عبارت دیگر، گرما به وسیله رسانش هنگامی که اتمهای مجاور در برابر دیگری ارتعاش میکنند یا الکترونها از یک اتم ...
اموزش متلب_pdepe(حل عددی معادله حرارت پاره ای وابسته به زمان)
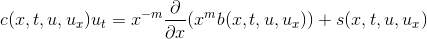
امروز قراره معادلات گرمایی در فضای تک بعد رو با چند مثال بررسی کنیم. برای حل معادله گرما در زمان t و در فضای تک بعدی از دستور pdepe استفاده می کنیم.فرم کلی معادله سھمی وار متلب بصورت زیر می باشد.و ھمین طور فرم کلی شرایط مرزی بصورت زیر می باشد.که xl نمایانگر نقطه ابتدا و xr نمایانگر نقطه انتهایی شرایط مرزی می باشد.توجه کنید که b دارای مقدار ثابت در هر دو معادله است.هر کدام از معادله های بالا را در m.file جداگانه قرار می دهیم.مقادیر s,b,c را از مقایسه معادله حاکم در مثال با فرم کلی معادله سهمیگون در متلب بدست اورده و در m.file قرار می دهیم.مقادیر p,q را نیز از مقایسه شرایط مرزی مسئله با فرم کلی شرایط مرزی تعریف شده برای متلب بدست می اوریم.و در اخر نیز شرایط کرانه ای را در m.file سوم قرار می دهیم.سپس به کمک دستور pdepe سه m.file را ترکیب کرده معادله را حل می کنیم.:Exampleمعادله اصلی بصورت:شرایط مرزی بصورت: و شرایط اولیه بصورت:کاملا مشخص است که مقدار c=1 می باشد.همچنین ما در طرف راست معادله حاکم بر مسئله مشتق دوم بر حسب x را داریم.پس مقدار b باید برابر ux باشد.مقدار s نیز که به وضوح مشخص است که برابر 0 می باشد. ملاحضه کردید که مقادیر c,b,s طوری در معادله سهمیگون مقدار دهی شدند که به معادله حاکم بر مسئله برسیم.مقدار m نیز باید برابر 0 باشد تا عملا x از معادله حذف شود. m را در اخر مقدار دهی میکنیم.کد زیر نمایانگر معادله اصلی و در eqn1.m ذخیره می کنیم. function [c,b,s] = eqn1(x,t,u,DuDx)%EQN1: MATLAB function M-file that specifies%a PDE in time and one space dimension.c = 1;b = DuDx;s = 0;برای شرایط مرزی نیز مطابق معادله اصلی عمل می کنیم. برنامه نویسان شرایط مرزی را بگونه ای به فرم بالا در اورده اند تا برای تمامی معادلات عمومیت داشته باشد.ما با تعیین ضرایب بگونه ای عمل می کنیم تا فرم کلی شرایط مرزی تبدیل به شرایط مرزی مثال شود.به شرایط ابتدایی دقت کنید.مقدار q برابر 0 است تا b حذف شود.در متیجه p برابر با u می شود.و برای شرایط انتهایی نیز به همین صورت, q برابر صفر و مقدار p برابر با u-1 است.حالا نتایج رو در فایل bc1 ذخیره می کنیم.function [pl,ql,pr,qr] = bc1(xl,ul,xr,ur,t)%BC1: MATLAB function M-file that specifies boundary conditions%for a PDE in time and one space dimension.pl = ul;ql = 0;pr = ur-1;qr = 0;و همینطور شرط اولیه را در initial1.m ذخیره می کنیم.function value = initial1(x)%INITIAL1: MATLAB function M-le that species the initial condition%for a PDE in time and one space dimension.value = 2*x/(1+x^2);و حالا نوبت به حل مساله به کمک دستور pdepe رسیده است.مساله را در زمان 10ثانیه نخست و طول واحد(مثلا یک لوله به طول واحد) حل می کنیم.%PDE1: MATLAB script M-file that solves and plots%solutions to the PDE stored in eqn1.mm = 0;% NOTE: m=0 specifies no symmetry in the problem. Taking% m=1 specifies cylindrical symmetry, while m=2 specifies% spherical symmetry.%% Define the ...
الگوریتم حل معادله گرما
دانشجویان گرامی درس ریاضیات مهندسی میتوانند الگوریتم حل معادله گرما را از اینجا دانلود نمایند.
الگوریتم حل معادلات گرما و موج
دانلود الگوریتم حل معادله گرما و الگوریتم حل معادله موج
شیمی و مکانیک
حل معادلات گرما به روش کرانک نیکلسون، FTCS،پیشرو، پسرو، اویلر، صریح و ضمنی و ... حل معادلات دیفرانسیل غیر خطی به روش اختلاف محدود (Finite Difference) حل عددی معادله گرما دو بعدی در یک صفحه نا متفارن حل مسائل انتقال حرارت به روش تفاضل محدود (Finite Difference) حل مسائل انتقال حرارت مانند یافتن نقاط درونی صفحه و انتقال حرارت در اثر عبور هوا از روی استوانه محاسبه ضریب اصطحکاک با معادله کلبروک جریان در لوله های ساده تعیین ثابت تعادل برای محلول های حقیقی محاسبات تعادل گاز-مایع، نقطه حباب ، نقطه شبنم بدست آوردن ضرایب معادله آنتوان برای آب با استفاده از رگرسیون حل مسائل CFD با فولئنت و گمبیت محاسبه و شبیه سازی ضریب درگ کره و نیم کره و رسم خطوط جریان و کانتور فشار محاسبه حجم ویژه با استفاده از معادلات حالت SRK،vdw، PR، Schmidt and wenzelو Patel and Teja حل معادله لاپلاس بر روی صفحه به روش ژاکوبی حل معادله لاپلاس بر روی صفحه به روش گاوس سایدل محاسبه توزیع دما در یک دیواره به روش FTCS ،روش DuFort-Frankel ،روش Laasonen ،روش Crank-Nicolson ،روش Laasonen حل معادله بلازیوس blasiusبه روش رانگ کوتا و shooting method محاسبه و رسم نقشه های منحنی باقی مانده برای مخلوط ها (Residue curve maps) شبیه سازی جذب سطحی ( Adsorption isotherm ) با سه مدل لانگمیر، فرندلیش، تمکین Freundlich، langmir، Temkin به همراه مقاله. رسم نمودار فشار بر حسب دما به کمک معادله آنتوان رسم نمودار فشار بر حسب حجم مولی در مدل RedlichKwong محاسبه جریان درون لوله و عدد رینولدز به کمک روابط سوامی و جین و دارسی-ویسباخ حل مساله انتقال حرارت هدایتی توزیع دمایی در یک صفحه در حالت ناپایا را با استفاده از روش خط یا اختلاف محدود finite difference بررسی نحوه انتقال حرارت در یک دیوار ساختمانی برقراری تعادل دینامیکی و استاتیکی در آزمایش بالانس با متلب بدست آوردن کانتورهای دما در یک کانال جریان و حل معادله لاپلاس با روش تفاضلات محدود انجام محاسبات فلش به همراه رابط گرافیکی کاربر GUI محاسبه نقطه حباب و نقطه شبنم در فشار یا دمای ثابت با معادله PR شبیه سازی استخراج مایع مایع به همراه برگشتی شبیه سازی کنترل فشار و دبی خروجی بدست آوردن پروفایل دما در سطح مقطع steak در زمان های مختلف بعد از قرار گرفتن در ظرف روغن محاسبات خواص مخلوط mix)) برای ترکیب آدیاباتیک چند جریان شبیه سازی راکتور batch (ناپیوسته) و رسم نمودار غلظت ها ریشه معادله درجه سه با استفاده از روابط کلی (Perry's Chemical Engineers' Handbook) تعیین ضرایب مدل UNIQUAC برای مخلوط آب-متانول مقدار ضریب فوگاسیته را برای فشار های مختلف با معادلات حالت VdW وPR بررسی ارتعاشات مدل ساده شده یک هواپیما دارای چهار موتور محاسبه ماتریس سختی ...
انتقال گرما

گرما گرما نوعی انرژی است که به علت اختلاف دما بین دو سیستم، از یکی به دیگری منتقل میشود. (گرما همواره در حال عبور از مرزهای سیستم است.)دماکمیتی است بیانگر مقدار گرمای یک جسم. دما معیاری است برای تعیین میزان گرمی یا سردی یک جسم.یکای این کمیت در سیستم متریک درجه کلوین میباشد. سایر واحدهای این کمیت عبارتاند از:درجه سلسیوس (درجه سانتیگراد) درجه فارنهایت درجه رانکین نیز واحدی برای اندازه گیری دما است. ۲ واحد سانتی گراد و فارنهایت دمای نسبی، و ۲ واحد کلوین و رانکین دمای مطلق هستند. در واقع کلوین همان صفر مطلق در سیستم متریک است.برخی از دماهای مهمموضوع دما بر حسب سانتیگرادنقطهٔ جوش هیدروژن مایع ۲۳۵- نقطهٔ جوش اکسیژن مایع ۱۸۳- نقطهٔ انجماد الکل ۱۱۵- نقطهٔ انجماد جیوه ۳۹- نقطهٔ ذوب یخ ۰ دمای بدن انسان سالم ۳۷ نقطهٔ جوش الکل ۷۹ نقطهٔ جوش آب ۱۰۰ نقطهٔ جوش جیوه ۳۵۷ نقطهٔ ذوب طلا ۱۰۶۷ دمای هستهٔ زمین ۳۷۰۰ دمای سطح خورشید ۵۷۰۰ سامانه سامانه یا سیستم (به انگلیسی: System) مجموعه یا گروهی از اشیاء مرتبط یا غیر مرتبط است که هدف یا اهدافی خاص را دنبال میکنند، به گونهای که واحدی پیچیده را تشکیل دهند.سامانه یا سیستم (منظومه، و دستگاه هم گفته شده است؛ مانند: منظومهء شمسی - Solar system، و دستگاه معادلات خطّی - System of linear equations) چیدهای از عناصر پیوستهای است که یک تمامیت یگانه را تشکیل میدهند. چنین ترکیب و چیدهای معمولاً مجموعهای منظم را درست میکند و به همین رو به آن سامانه میگویند که از واژه پارسی سامان به معنی نظم و ترتیب گرفته شدهاست. به بخشی از یک سامانه که خود جزئی از یک سامانه دیگر باشد زیرسامانه میگویند. یک سامانه معمولاً دربرگیرنده بخشها و عناصری است که بهم پیوسته شدهاند تا جریان و روند دادهها، ماده یا انرژی را آسان تر سازند. یک سامانه معمولاً واحدهایی دارای برهمکنش دارد که برای آنها میتوان الگوهای ریاضی تشکیل داد.شرط انتقال حرارتشرط انتقال حرارت خود به خودی، اختلاف دما است. اگر دو سیستم در حال ارتباط با یکدیگر همدما نباشند، گرما از ناحیهٔ پر دما (گرم) به ناحیهٔ کم دما (سرد) جریان مییابد. و این جریان تا زمانی ادامه مییابد که دو سیستم همدما شوند.چون گرما به دلیل وجودِ گرادیان دمایی شارش مییابد، دانستن توزیع دما ضروری است.گرادیاندر حسابان بردارها گرادیانِ یک میدان نردهای، میدانی برداریاست که مؤلفههای آن نرخ تغییر میدان نخستین را در جهتهای مختلف نشان میدهد. جهت خود میدان برداری گرادیان جهت بیشینهٔ تغییرات است.به تعبیر دیگربرداری را که اندازه و جهت حد اکثر ...
حل معادله گرما يک بعدي غير دائم با روش ضمني کرانک نيکلسون
همانطور که ميدانيم براي حل معادلات ديفرانسيل جزئي ما از روشهاي عددي استفاده ميکنيم. يکي از روشهاي عددي روش تفاضلات محدود است که روش کرانک نيکلسون هم يکي از روشهاي ضمني بي قيد و شرط پايدار است. در فايل زير که براي دانلود گذاشتم روند حل کاملا توضيح داده شده است.حجم:395کیلوبایتدانلودرمز:www.laminar.blogfa.com
حل معادله حرارت با نرم افزار متلب (matlab)
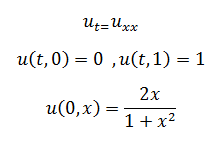
معادله حرارت (Heat equation) یک معادله دیفرانسیل پارهای خطی است. برای حل معادله گرما با زمان t وفضای تک بعد x از تابع pdepe استفاده می کنیم. فرض کنید برای مثال مایلیم معادله گرمای زیر را حل کنیم: (با تشکر از جناب مسعود شمس) دریافت فایل
گزارش کار انتقال حرارت
عنوان: گزارش کار آزمایشگاه حرارت آزمایش اول: محاسبه ضریب هدایت حرارتی(k)
