مساحت پنج ضلعی
چند ضلعی های منتظم
در هندسه اقلیدسی، یک چندضلعی منتظم، چندضلعی است که همه زوایا واضلاع آن هماندازهاند. چندضلعیهای منتظم، میتوانند کوژ و یا به شکل ستاره باشند. در حالت حدی، یک دنباله از چندضلعیهای منتظم با افزایش تعداد اضلاع، در صورت ثابت ماندن محیط بهدایره تبدیل میشود و در صورت ثابت ماندن طول ضلع، به apeirogon تبدیل میشود. محتویات [نهفتن] ۱ ویژگیها ۲ چندضلعیهای منتظم کوژ ۲.۱ زاویهها ۲.۲ قطرها ۲.۳ مساحت ۳ چندضلعیهای منتظم ستارهای ۴ جستارهای وابسته ۵ پانویس ویژگیها[ویرایش] ویژگیهای بیانشده در ادامه، برای همهٔ چندضلعیهای منتظم (اعم از کوژ وستارهای) برقرار است. یک چندضلعی منتظم n-ضلعی، تقارن چرخشی از مرتبهٔ n دارد. همهٔ رأسهای یک چندضلعی منتظم بر روی یک دایره (دایره محیطی) قرار میگیرند. بهعبارت دیگر، رأسها نقاطی همدایره هستند. یعنی یک چندضلعی منتظم، لزوماً یک چندضلعی دایرهای هم هست. هر چندضلعی منتظم، یک دایره محاطی دارد که به همه اضلاع در نقطهٔ وسط آنهامماس است. بنابراین هر چندضلعی منتظم، لزوماً یک چندضلعی مماسی هم هست. یک n-ضلعی منتظم با استفاده از خطکش و پرگار قابل ترسیم است؛ اگر و تنها اگر فاکتورهای اول فرد n، اعداد اول فرمای متفاوتی باشند. چندضلعیهای منتظم کوژ[ویرایش] همهٔ چندضلعیهای سادهٔ منتظم، کوژ هستند. چندضلعیهای منتظم باتعداد اضلاع یکسان، متشابه هستند. یک n-ضلعی منتظم کوژ، بانماد شلفلی {n} نشان داده میشود. مثلثمتساویالاضلاع{۳} مربع{۴} پنجضلعی{۵} ششضلعی{۶} هفتضلعی{۷} هشتضلعی{۸} نهضلعی{۹} دهضلعی{۱۰} یازدهضلعی{۱۱} دوازدهضلعی{۱۲} سیزدهضلعی{۱۳} چهاردهضلعی{۱۴} پانزدهضلعی{۱۵} شانزدهضلعی{۱۶} هفدهضلعی{۱۷} هجدهضلعی{۱۸} نوزدهضلعی{۱۹} بیستضلعی{۲۰} سیضلعی{۳۰} چهلضلعی{۴۰} پنجاهضلعی{۵۰} شصتضلعی{۶۰} هفتادضلعی{۷۰} هشتادضلعی{۸۰} نودضلعی{۹۰} صدضلعی{۱۰۰} زاویهها[ویرایش] برای یک n-ضلعی منتظم کوژ، اندازهٔ هر زاویهٔ داخلی برابر است با: یا درجهیا رادیان و اندازهٔ هر زاویه خارجی آن برابر است با درجه. قطرها[ویرایش] برای n > ۲، تعداد قطرهای n-ضلعی، برابر است با ، بهعنوان مثال برای مثلث، چهارضلعی، پنجضلعی و ششضلعی، تعداد قطرها بهترتیب، ۰، ۲، ۵ و ۹ است. برای یک n-ضلعی منتظم محاطشده در یک دایره به شعاع واحد، حاصلضرب فاصلهٔ هر رأس تا همهٔ رأسهای دیگر، برابر است با n. مساحت[ویرایش] پنجضلعی منتظم با طول ضلع s، شعاعدایره محیطی r و شعاع دایره محاطی a مساحت یک n-ضلعی منتظم کوژ با اندازهٔ ضلع s، شعاع دایره ...
یافتن مساحت شکل های غیر هندسی و غیر منتظم
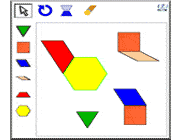
دانش آموزان می توانند علاوه بر کنار هم چیدن شکل های کاغذی، از فعالیت کامپیوتری "جورچین" برای ساختن طرح های خود استفاده کنند و یک نسخه از آن را برای اندازه گیری و محاسبه مساحت شکل چاپ کنند. (همچنین دانش آموزان می توانند مساحت یک مثلث را به عنوان واحد در نظر بگیرند و مساحت بقیه اشکال را با آن بسنجند. به عنوان مثال یک متوازی الاضلاع از دو مثلث درست شده، پس مساحت آن 2 واحد است.) فعالیت کامپیوتری "جورچین"در کلاس در مورد مراحل تعیین مساحت هر شکل و به دست آوردن مجموع مساحت ها بحث کنید. دانش آموزان باید مساحت هر شکل را حساب کرده و مقدار آن را روی شکل یادداشت کنند و بعد باید مجموع مساحت شکل ها را حساب کنند تا مساحت شکل اصلی به دست آید. برای دانش آموزان توضیح دهید که ترکیب،همان طور که انجام دادند، فرایند کنار هم گذاشتن شکل ها برای ساختن یک شکل تازه است. در مقابل تجزیه، عمل خرد کردن شکل به قطعات کوچکتر است، که آن ها برای پیدا کردن مساحت کل شکل انجام دادند. به آن ها بگویید که از عمل تجزیه برای تعیین مساحت فضاهای بزرگتر استفاده خواهند کرد. یک اتاق با شکل هندسی غیر منتظم را در مدرسه خود تعیین کنید. (به این معنی که این اتاق باید کاملاً به شکل مستطیل نباشد. و اگر ممکن است جایی را پیدا کنید که تعدادی زاویه غیر 90 درجه داشته باشد.) حالا این اتاق را به عنوان مبنا در نظر بگیرید و پرسشی مانند پرسش زیر یا شبیه آن را برای دانش آموزان مطرح کنید: مدیر مدرسه ما می خواهد بداند چه اندازه موکت (یا کاشی) برای پوشاندن تمام کف این اتاق نیاز دارد؟ او می خواهد مساحت دقیق اتاق را بداند، زیرا نمی خواهد بیش از میزان لازم موکت بخرد که پولش را هدر دهد. همچنین نمی خواهد که کم تر از نیاز سفارش دهد که نتوان با آن تمام زمین را فرش کرد. کار شما اندازه گیری ابعاد این اتاق و محاسبه مساحت آن است. سپس باید نامه ای به مدیر بنویسید و به او اطلاع دهید چه مقدار موکت باید بخرد و توضیح دهید که چگونه به پاسخ خود رسیدید. در صورت امکان دانش آموزان را به اتاق مورد نظر ببرید تا ابعاد آن را اندازه بگیرند، و اگر این امکان را ندارید، پلان آن اتاق را در اختیار آن ها قرار دهید. همچنین می توانید به جای کار بر روی اتاقی در مدرسه خودتان، نقشه اتاق های خاصی را با شکل هندسی غیر منتظم به آن ها بدهید، مثل نقشه رصدخانه سلطنتی در گرینویچ انگلستان. یک مثال متفاوت در تصویر زیر نشان داده شده است: دانش آموزان باید در گروه های دو نفره مساحت کف این اتاق را با استفاده از روش هایی که تا این جا یاد گرفته اند محاسبه کنند. برخی گروه ها ممکن است اتاق را به چندضلعی های ساده تر تجزیه کنند ...
زوایای داخلی چند ضلعی
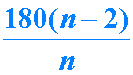
با استفاده از فرمول زیر می توان اندازه هر یک از زاویه ها را بدست آورد.n تعداد اضلاع است و جواب بدست آمده همان اندازه یک زاویه است. البته توجه داشته باشید که چند ضلعی باید منتظم باشد.نه مانند شکل زیر: مثال۱:اگر هر یک از زاویه های چند ضلعی ۱۳۵ درجه باشد،تعداد اضلاع این چند ضلعی چند تاست؟ مثال۲:هر یک از زاویه های داخلی یک دوازده ضلعی را بیابید؟
چهار ضلعی ها
خطوط موازی دو خط واقع بر یک صفحه را موازی می گوییم هر گاه آن دو خط بر هم منطبق باشند و یا هیچ نقطه ی مشترکی نداشته باشند .مانند دو خط1 d و 2 d که با هم موازیند. می نویسیم: میخوانیم: خط های 1 d و 2 d با هم موازیند. توضیح تصویری: چهار ضلعی ها: هر چهار ضلعی دارای چهار ضلع و چهار رأس می باشد. دو ضلع چهار ضلعی که در یک رأس مشترک باشند دو ضلع مجاور نام دارد. دو ضلع که نقطه مشترک ندارند ، دو ضلع مقابل نام دارد. انواع چهار ضلعی ها : 1) متوازی الاضلاع: چهار ضلعی است که اضلاع آن دو بدو موازی باشند خواص متوازی الاضلاع : در هر متوازی الاضلاع زاویه های مجاور مکمل اند و زاویه های مجاور مقابل مساویند . در هر متوازی الاضلاع ضلع های مقابل با هم برابرند. در هر متوازی الاضلاع قطر ها یکدیگر را نصف می کنند. 2) مستطیل: چهار ضلعی که تمام زاویه های آن قائمه باشد به عبارت دیگر مستطیل متوازی الاضلا عی است که یک زاویه ی قائمه داشته باشد . خواص مستطیل: چون مستطیل نوعی متوازی الاضلاع است پس تمام خواص متوازی الاضلاع را داراست . قطر های مستطیل با هم برابرند. 3) لوزی : چهار ضلعی که چهار ضلع آن مساوی باشند لوزی است . خواص لوزی: چون لوزی نوعی متوازی الاضلاع است پس همه ی خواص متوازی الاضلا ع را داراست . قطرهای لوزی بر هم عمودند هر قطر لوزی نیمساز دو زاویه ی مقابل لوزی است . 4) مربع : چهار ضلعی است که چهار ضلع آن مساوی و چهار زاویه ی آن قائمه هستند . بنابراین مربع هم نوعی لوزی، هم نوعی مستطیل و در نتیجه نوعی متوازی الاضلاع است. پس تمام خواص آن ها را داراست ذوزنقه : چهار ضلعی است که فقط دو ضلع آن با هم موازی باشند . در ذوزنقه دو ضلع موازی را قاعده و دو ضلع غیر موازی را ساق های ذوزنقه می گویند خواص ذوزنقه: در ذوزنقه زاویه های مجاور به هر ساق مکمل یکدیگرند انواع ذوزنقه : ذوزنقه قائم الزاویه : ذوزنقه ای است که یک ساق آن بر دو قاعده عمود شده باشد ذوزنقه متساوی الساقین : ذوزنقه ای است که دو ساق آن با هم برابر باشد . 1- مجموع زاویه های داخلی هر چهار ضلعی 360 است A+B+C+D=۳۶۰ 2- مجموع زاویه های خارجی هر n ضلعی 360 است . 3- هر گاه از رئوس یک چهار ضلعی چهار خط به موازات قطرها آن رسم کنیم متوازی الاضلا عی بدست می آید که مساحت آن دو برابر مساحت چهار ضلعی اولیه می باشد . 4- مجموع زوایای داخلی هر n ضلعی از دستور 180×( 2 n -) بدست می آید (n ضلعی محدب) مثال Å مجموع زوایای داخلی یک هشت ضلعی را بدست آورید . ...
روش محاسبه سطح مثلث و اشکال هندسی
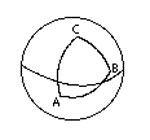
مثلث ار اساسی ترین اشکال در هندسه میباشد.یک مثلث دارای سه راس است که سه ضلع این رئوس را به هم وصل میکند.در هندسه اقلیدسی این اضلاع خطوطی مستقیم هستند. ولی در هندسه کروی این اضلاع کمان هایی از دایره عظیمه میباشند.این دو نوع مثلث را میتوانید در شکلهای روبرو مشاهده نمایید. انواع مثلثمثلث متساوی الاضلاع: مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای داخلی این مثلث نیز با هم برابرند.مثلث متساوی الساقین: مثلثی است که دارای دو ضلع با طولهای مساوی استو دو زاویه داخلی برابر دارد.البته مثلث میتواند دارای سه ضلع با طولهای مختلف و زوایای غیر مساوی باشد.مثلث قائم الزاویه: مثلثی را گویند که یکی از زوایای آن 90درجه باشد.نسبت های مثلثاتی مانند sin و cos ،بر روی مثلث قائم الزاویه تعریف میشوند.مثلث منفرجه: مثلثی را گویند که یکی از زوایای داخلی آن بیشتر از 90 درجه باشد.مثلث حاده : مثلثی را گویند که تمام زوایای داخلی آن کمتر از 90 درجه باشد.300 سال قبل از میلاد اقلیدس ،اصول اولیه درباره مثلث را ارائه داد.به عنوان مثال یکی از اصول مهم در مورد مثلث این است که مجموع زوایای داخلی یک مثلث برابر 180 درجه است. بر اساس این اصل میتوان با معلوم بودن دو زاویه از مثلث اندازه زاویه سوم را بدست آورد.یکی از مهمترین قضایای موجود در مثلثات قضیه فیثاغورث میباشد.در این قضیه رابطه بین وتر و اضلاع قائم یک مثلث قائم الزاویه بیان میشود. محاسبه مساحت مثلثبرای محاسبه مساحت یک مثلث روشهای مختلفی وجود داردو در ادامه به توضیح این روشها میپردازیم روش هندسیبرای محاسبه مساحت یک مثلث باید طول ارتفاع مثلث و نیز طول قاعده(ضلعی که ارتفاع بر آن عمود است) آن را داشته باشیم.آنگاه میتوانیم از فرمول زیر استفاده کنیم: در این فرمول b طول قاعده و h طول ارتفاع مثلث میباشد. در شکل زیر نحوه بدست آمدن این فرمول بیان شده است: تبدیل مثلث به یک متوازی الاضلاع که دو برابر مثلث مساحت دارد وسپس تبدیل متوازی الضلاع به یک مستطیلبرای پیدا کردن مساحت مثلث (قسمت سبز) ابتدا یک کپی از مثلث (قسمت آبی) را برداشته و آن را 180 درجه میچرخانیم و به مثلث اولیه متصل میکنیم تا یک متوازی الاضلاع بدست آید. با بریدن قسمتی از متوازی الاضلاع و متصل کردن آن به ضلع دیگر آن(همانند شکل) یک مستطیل ایجاد میشود. چون مساحت مستطیل برابر bh است .پس مساحت مثلث اولیه، نصف این مساحت خواهد بود.روش برداری محاسبه مساحت متوازی الاضلاع با استفادهاز ضرب خارجی دو بردارمساحت یک متوازی الاضلاع را میتوان با استفاده از بردارها محاسبه کرد.اگر AB,AC را مطابق شکل فرض کنیم آنگاه مساحت ABCD برابر |AB × AC| خواهد بود.این ...
حجم ومساحت اشکال هندسی /ریاضی ششم
دانش آموزان عزیز :در ایام تعطیلات نوروز با مطالعه و تمرین بخش مساحت و حجم به اطلاعات خود در این زمینه بیفزایید حجم:(Volume) حجم در لغت به معنی برآمدگی و ستبری و جسامت چیزی می باشد و در اصطلاح هندسه گنجایش و ظرفیت جسم و آن مقداری از فضا که جسم آن را اشغال می کند, را نشان می دهد. منشور: (Prism) منشور در لغت به معنی پراکنده, نشر شده, زنده شده و مبعوث است و در اصطلاح هندسه نام شکلی است که دو قاعده دارد که دو چند ضلعی مساوی هستند و بدنه منشور(سطح جانبی منشور ) از مستطیلها یا متوازی الاضلاع ها تشکیل شده است. معرفی منشور 5 پهلو: í نام شکل: منشور 5 پهلو í یال های منشور: 'EE',DD',CC',BB',AA í وجه منشور: هر کدام از مستطیل های جانبی را یک وجه منشور می نامند. í ارتفاع منشور: از آنجا که هر کدام از یال ها بر دو قاعده منشور عمود می باشند, لذا ارتفاع منشور با اندازه هر یک از یال ها برابر است. í قاعده ی منشور: منشور دو قاعده دارد. ABCDE و 'A'B'C'D'E که دو پنج ضلعی مساوی اند. رابطه های مهم: ارتفاع × مساحت قاعده = حجم منشور ارتفاع × محیط قاعده = مساحت جانبی منشور مساحت دو قاعده + مساحت جانبی = مساحت کل منشور استوانه: (Cylinder) نام شکلی است که دو قاعده دارد که دو دایره مساوی هستند و بر جانبی راست استوار است. اگر مستطیل را حول طول آن دوران دهیم, شکل فضایی حاصل استوانه نامیده می شود. در این صورت طول مستطیل ارتفاع استوانه و عرض آن شعاع قاعده استوانه می باشد. در شکل بالا مستطیل ABCD را حول طول آن دوران داده ایم و استوانه بوجود آمده است. رابطه های مهم: ارتفاع×مساحت قاعده(دایره) = حجم استوانه ارتفاع×محیط قاعده(دایره) = مساحت جانبی استوانه مساحت دو قاعده + مساحت جانبی = مساحت کل استوانه هرم: (pyramid) هرم در لغت به معنی سخت پیر گردیدن و کلان سال شدن است و در اصطلاح هندسه حجمی است که قاعده آن یک چند ضلعی و وجوه جانبی اش مثلثهایی باشند که همه به یک رأس مشترک(رأس هرم) منتهی می شوند. معرفی هرم منتظم: í نام شکل: هرم منتظم. í رأس هرم: نقطه S í ارتفاع هرم: پاره خطی است که از رأس هرم به مرکز قاعده ی هرم عمود است(SO) í قاعده هرم: پنج ضلعی منتظم ABCDE í سهم هرم: ارتفاع مثلث های جانبی, ارتفاع هر وجه جانبی هرم منتظم(SH). í وجه هرم: هر یک از مثلث هایی که بدنه هرم را می پوشانند را یک وجه جانبی می نامیم. í یال هرم: محل تقاطع هر دو وجه جانبی را یال هرم می نامیم. SE,SD,SC,SB,SA رابطه های مهم: مخروط : (cone) مخروط به معنی خراشیده شده ، تراشیده شده و خراطی شده است ودر اصطلاح هندسه حجمی است که از دوران مثلث قائم الزاویه حول یک ضلع آن به دست می آید . کله قند و کلاه بوقی ...
