مساحت مثلث مختلف الاضلاع
ارتفاع در مثلث
مساحت مثلث مساحت یک مثلث برابر یک دوم طول یک ضلع، ضرب در طول ارتفاع وارد بر آن، یعنی فاصله رأس سوم تا خط شامل ضلع انتخابشده، است. مساحت مثلث را از رابطه زیر به دست میآورند: مساحت مثلث = ( قاعده × ارتــــــفاع ) ÷ 2 مساحت مثلث را با انتخاب هركدام از ارتفاع هاي آن كه به دست آوريم، حاصل يك عدد خواهد بود. محیط مثلث محیط مثلث را از رابطه زیر به دست میآورند: محیط مثلث = مجموع سه ضلع مساحت هر نوع مثلث بدون دانستن ارتفاع فرض میکنیم a و b و c اضلاع یک مثلث از هر نوع داده شده باشد (خواه قائم الزاویه - متساوی الساقین - مختلف الاضلاع) فرمول زیر مساحت مثلث را بیان میکند: (if a+b+c=2p → s^2=p(p-a)(p-b)(p-c → یعنی → توان دوم مساحت مثلث از این فرمول بهدست میآید با یک بار جذر گرفتن از آن مساحت مثلث را خواهیم داشت. مرکز دایره محاطی محل برخورد نیمسازهای زوایای مثلث است. با دانستن خصوصیات بعضی از خطوط مانند ارتفاع یا عمود منصف و یا میانه میتوانیم به نتایج جالبی در مورد دست پیدا کنیم. برخی از این نتایج را بیان میکنیم: اگر بر سه ضلع مثلث خطوطی را عمود میکنیم به طوریکه این خطوط اضلاع را نصف نمایند.(در واقع عمود منصف اضلاع را رسم میکنیم)در این صورت محل برخورد این سه خط، مرکز دایرهای خواهد بود که مثلث را احاطه میکند . به این دایره، دایره محاطی گویند.این دایره طوری رسم میشود که از سه راس مثلث عبور کند. طبق قضیه فیثاغورث اگر مرکز دایره محاطی روی یکی از اضلاع قرار گیرد آنگاه زاویه مقابل آن ضلع قائم خواهد بود.به عبارتی دیگر مثلث ما قائم الزاویه خواهد بود. اگر مرکز دایره درون مثلث باشد، مثلث ما یک مثلث حاده خواهد بود و اگر بیرون مثلث باشد، مثلث از نوع منفرجه خواهد بود. ارتفاع مثلث خط راستی است که از یک راس مثلث عبور کرده و بر ضلع مقابل آن راس عمود میشود.ضلعی را که ارتفاع بر آن عمود است را قاعده مثلث گویند.طول ارتفاع، فاصله بین راس و قاعده نظیر ارتفاع است.اگر سه ارتفاع مثلث را رسم کنیم این سه ارتفاع همدیگر را در داخل مثلث قطع میکنند مگر در حالتی که مثلث، منفرجه باشد. محل برخورد نیمسازهای مثلث مرکز دایره محیطی است. نیمسازهای مثلث نیمساز یک زاویه از مثلث خط راستی است که از یک راس مثلث گذشته و آن زاویه را به دو قسمت مساوی تقسیم کند. اگر نیمسازهای سه زاویه مثلث را رسم کنیم این خطوط در نقطهای درون مثلث همدیگر را قطع خواهند کرد.این نقطه مرکز دایره محاطی مثلث خواهد بود.این دایره درون مثلث قرار دارد به طوریکه اضلاع مثلث، خطوطی مماس بر دایره هستند. میانههای مثلث میانه یک مثلث خط راستی است که از راس مثلث گذشته و ضلع مقابل آن را به دو قسمت مساوی ...
مثلث

مُثَلَث مثلث (سهگوش) شکلی مسطح است که از اتصال سه نقطه غیرهمخط در صفحه به وجود میآید. مثلث دارای سه ضلع و سه زاویه است. مساحت مثلث مساحت یک مثلث برابر یک دوم طول یک ضلع، ضرب در طول ارتفاع وارد بر آن، یعنی فاصله رأس سوم تا خط شامل ضلع انتخابشده، است. مساحت هر نوع مثلث بدون دانستن ارتفاع فرض میکنیم a و b و c اضلاع یک مثلث از هر نوع داده شده باشد (خواه قائم الزاویه - متساوی الساقین - مختلف الاضلاع) فرمول زیر مساحت مثلث را یبان میکند : if a+b+c=2p → s2=p(p-a)(p-b)(p-c)→ یعنی → توان دوم مساحت مثلث از این فرمول یدست میآید با یک بار جذر گرفتن از آن مساحت مثلث را خواهیم داشت مرکز دایره محاطی محل برخورد عمود منصف های اضلاع مثلث است. با دانستن خصوصیات بعضی از خطوط مانند ارتفاع یا عمود منصف و یا میانه میتوانیم به نتایج جالبی در مورد دست پیدا کنیم. برخی از این نتایج را بیان میکنیم: اگر بر سه ضلع مثلث خطوطی را عمود میکنیم به طوریکه این خطوط اضلاع را نصف نمایند.(در واقع عمود منصف اضلاع را رسم میکنیم)در این صورت محل برخورد این سه خط، مرکز دایره ای خواهد بود که مثلث را احاطه میکند . به این دایره، دایره محاطی گویند.این دایره طوری رسم میشود که از سه راس مثلث عبور کند. طبق قضیه فیثاغورث اگر مرکز دایره محاطی روی یکی از اضلاع قرار گیرد آنگاه زاویه مقابل آن ضلع قائم خواهد بود.به عبارتی دیگر مثلث ما قائم الزاویه خواهد بود. اگر مرکز دایره درون مثلث باشد ،مثلث ما یک مثلث حاده خواهد بود و اگر بیرون مثلث باشد، مثلث از نوع منفرجه خواهد بود. ارتفاع مثلث خط راستی است که از یک راس مثلث عبور کرده و بر ضلع مقابل آن راس عمود میشود.ضلعی را که ارتفاع بر آن عمود است را قاعده مثلث گویند.طول ارتفاع ، فاصله بین راس و قاعده نظیر ارتفاع است.اگر سه ارتفاع مثلث را رسم کنیم این سه ارتفاع همدیگر را در داخل مثلث قطع میکنند مگر در حالتی که مثلث ،منفرجه باشد. محل برخورد نیمسازهای مثلث مرکز دایره محیطی است. نیمساز یک زاویه از مثلث خط راستی است که از یک راس مثلث گذشته و آن زاویه را به دو قسمت مساوی تقسیم کند. اگر نیمسازهای سه زاویه مثلث را رسم کنیم این خطوط در نقطه ای درون مثلث همدیگر را قطع خواهند کرد.این نقطه مرکز دایره محیطی مثلث خواهد بود.این دایره درون مثلث قرار دارد به طوریکه اضلاع مثلث، خطوطی مماس بر دایره هستند. میانه یک مثلث خط راستی است که از راس مثلث گذشته و ضلع مقابل آن را به دو قسمت مساوی تقسیم میکند. سه میانه مثلث یکدیگر را در نقطه ای به نام مرکز مثلث قطع میکنند البته این نقطه مرکز ثقل مثلث نیز میباشدهمچنین این نقطه هر میانه مثلث را به نسبت 1 به 2 تقسیم ...
محیط و مساحت اشکال هندسی
دانستنی ها : نام شکل محیط مساحت تعداد خط تقارن تعداد قطرها مربع یک ضلع × 4 یک ضلع × خودش 4 2 مستطیل (طول + عرض) × 2 طول × عرض 2 2 متوازی الاضلاع (طول + عرض) × 2 قاعده × ارتفاع ندارد 2 ذوزنقه قائم الزاویه مجموع چهار ضلع مجموع دو قاعده × ارتفاع ÷ 2 ندارد 2 ذوزنقه متساوی الساقین مجموع چهار ضلع مجموع دو قاعده × ارتفاع ÷ 2 1 2 لوزی یک ضلع × 4 حاصل ضرب دو قطر ÷ 2 2 2 مثلث قائم الزاویه مجموع سه ضلع قاعده × ارتفاع ÷ 2 ندارد ندارد مثلث متساوی الساقین مجموع سه ضلع قاعده × ارتفاع ÷ 2 1 ندارد مثلث متساوی الاضلاع مجموع سه ضلع قاعده × ارتفاع ÷ 2 3 ندارد مثلث مختلف الاضلاع مجموع سه ضلع قاعده × ارتفاع ÷ 2 ندارد ندارد دایره قطر × 14/3 شعاع × شعاع × 14/3 بی نهایت بی نهایت
مثلث
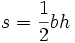
مثلث ار اساسی ترین اشکال در هندسه میباشد.یک مثلث دارای سه راس است که سه ضلع این رئوس را به هم وصل میکند.در هندسه اقلیدسی این اضلاع خطوطی مستقیم هستند. ولی در هندسه کروی این اضلاع کمان هایی از دایره عظیمه میباشند.این دو نوع مثلث را میتوانید در شکلهای روبرو مشاهده نمایید. انواع مثلث مثلث متساوی الاضلاع: مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای داخلی این مثلث نیز با هم برابرند. مثلث متساوی الساقین: مثلثی است که دارای دو ضلع با طولهای مساوی است و دو زاویه داخلی برابر دارد. البته مثلث میتواند دارای سه ضلع با طولهای مختلف و زوایای غیر مساوی باشد. مثلث قائم الزاویه: مثلثی را گویند که یکی از زوایای آن 90درجه باشد.نسبت های مثلثاتی مانند sin و cos ،بر روی مثلث قائم الزاویه تعریف میشوند. مثلث منفرجه: مثلثی را گویند که یکی از زوایای داخلی آن بیشتر از 90 درجه باشد. مثلث حاده : مثلثی را گویند که تمام زوایای داخلی آن کمتر از 90 درجه باشد. 300 سال قبل از میلاد اقلیدس ،اصول اولیه درباره مثلث را ارائه داد.به عنوان مثال یکی از اصول مهم در مورد مثلث این است که مجموع زوایای داخلی یک مثلث برابر 180 درجه است. بر اساس این اصل میتوان با معلوم بودن دو زاویه از مثلث اندازه زاویه سوم را بدست آورد. یکی از مهمترین قضایای موجود در مثلثات قضیه فیثاغورس میباشد.در این قضیه رابطه بین وتر و اضلاع قائم یک مثلث قائم الزاویه بیان میشود. محاسبه مساحت مثلث برای محاسبه مساحت یک مثلث روشهای مختلفی وجود داردو در ادامه به توضیح این روشها میپردازیم: روش هندسی برای محاسبه مساحت یک مثلث باید طول ارتفاع مثلث و نیز طول قاعده(ضلعی که ارتفاع بر آن عمود است) آن را داشته باشیم.آنگاه میتوانیم از فرمول زیر استفاده کنیم: در این فرمول b طول قاعده و h طول ارتفاع مثلث میباشد. در شکل زیر نحوه بدست آمدن این فرمول بیان شده است: تبدیل مثلث به یک متوازی الاضلاع که دو برابر مثلث مساحت دارد وسپس تبدیل متوازی الضلاع به یک مستطیل برای پیدا کردن مساحت مثلث (قسمت سبز) ابتدا یک کپی از مثلث (قسمت آبی) را برداشته و آن را 180 درجه میچرخانیم و به مثلث اولیه متصل میکنیم تا یک متوازی الاضلاع بدست آید. با بریدن قسمتی از متوازی الاضلاع و متصل کردن آن به ضلع دیگر آن(همانند شکل) یک مستطیل ایجاد میشود. چون مساحت مستطیل برابر bh است .پس مساحت مثلث اولیه، نصف این مساحت خواهد بود. روش برداری محاسبه مساحت متوازی الاضلاع با استفادهاز ضرب خارجی دو بردار مساحت یک متوازی الاضلاع را میتوان با استفاده از بردارها محاسبه کرد.اگر AB,AC را مطابق شکل فرض کنیم آنگاه مساحت ABCD برابر |AB × AC| ...
مثلث
مساحت یک مثلث برابر یک دوم طول یک ضلع، ضرب در طول ارتفاع وارد بر آن، یعنی فاصله رأس سوم تا خط شامل ضلع انتخابشده، است. مساحت هر نوع مثلث بدون دانستن ارتفاع فرض میکنیم a و b و c اضلاع یک مثلث از هر نوع داده شده باشد (خواه قائم الزاویه - متساوی الساقین - مختلف الاضلاع) فرمول زیر مساحت مثلث را یبان میکند : if a+b+c=2p → s2=p(p-a)(p-b)(p-c)→ یعنی → توان دوم مساحت مثلث از این فرمول یدست میآید با یک بار جذر گرفتن از آن مساحت مثلث را خواهیم داشت مرکز دایره محاطی محل برخورد عمود منصف های اضلاع مثلث است. با دانستن خصوصیات بعضی از خطوط مانند ارتفاع یا عمود منصف و یا میانه میتوانیم به نتایج جالبی در مورد دست پیدا کنیم. برخی از این نتایج را بیان میکنیم: اگر بر سه ضلع مثلث خطوطی را عمود میکنیم به طوریکه این خطوط اضلاع را نصف نمایند.(در واقع عمود منصف اضلاع را رسم میکنیم)در این صورت محل برخورد این سه خط، مرکز دایره ای خواهد بود که مثلث را احاطه میکند . به این دایره، دایره محاطی گویند.این دایره طوری رسم میشود که از سه راس مثلث عبور کند. طبق قضیه فیثاغورث اگر مرکز دایره محاطی روی یکی از اضلاع قرار گیرد آنگاه زاویه مقابل آن ضلع قائم خواهد بود.به عبارتی دیگر مثلث ما قائم الزاویه خواهد بود. اگر مرکز دایره درون مثلث باشد ،مثلث ما یک مثلث حاده خواهد بود و اگر بیرون مثلث باشد، مثلث از نوع منفرجه خواهد بود. ارتفاع مثلث خط راستی است که از یک راس مثلث عبور کرده و بر ضلع مقابل آن راس عمود میشود.ضلعی را که ارتفاع بر آن عمود است را قاعده مثلث گویند.طول ارتفاع ، فاصله بین راس و قاعده نظیر ارتفاع است.اگر سه ارتفاع مثلث را رسم کنیم این سه ارتفاع همدیگر را در داخل مثلث قطع میکنند مگر در حالتی که مثلث ،منفرجه باشد. محل برخورد نیمسازهای مثلث مرکز دایره محیطی است. نیمساز یک زاویه از مثلث خط راستی است که از یک راس مثلث گذشته و آن زاویه را به دو قسمت مساوی تقسیم کند. اگر نیمسازهای سه زاویه مثلث را رسم کنیم این خطوط در نقطه ای درون مثلث همدیگر را قطع خواهند کرد.این نقطه مرکز دایره محیطی مثلث خواهد بود.این دایره درون مثلث قرار دارد به طوریکه اضلاع مثلث، خطوطی مماس بر دایره هستند. میانه یک مثلث خط راستی است که از راس مثلث گذشته و ضلع مقابل آن را به دو قسمت مساوی تقسیم میکند. سه میانه مثلث یکدیگر را در نقطه ای به نام مرکز مثلث قطع میکنند البته این نقطه مرکز ثقل مثلث نیز میباشدهمچنین این نقطه هر میانه مثلث را به نسبت 1 به 2 تقسیم میکند به طوریکه فاصله میان راس مثلث تا این نقطه دو برابر فاصله این نقطه تا نقطه میانی ...
مثلث
مساحت مثلث مساحت یک مثلث برابر یک دوم طول یک ضلع، ضرب در طول ارتفاع وارد بر آن، یعنی فاصله رأس سوم تا خط شامل ضلع انتخابشده، است. مساحت مثلث را از رابطه زیر به دست میآورند: مساحت مثلث = ( قاعده × ارتــــــفاع ) ÷ 2 مساحت مثلث را با انتخاب هركدام از ارتفاع هاي آن كه به دست آوريم، حاصل يك عدد خواهد بود. [ویرایش] محیط مثلث محیط مثلث را از رابطه زیر به دست میآورند: محیط مثلث = مجموع سه ضلع [ویرایش] مساحت هر نوع مثلث بدون دانستن ارتفاع فرض میکنیم a و b و c اضلاع یک مثلث از هر نوع داده شده باشد (خواه قائم الزاویه - متساوی الساقین - مختلف الاضلاع) فرمول زیر مساحت مثلث را بیان میکند: (if a+b+c=2p → s^2=p(p-a)(p-b)(p-c → یعنی → توان دوم مساحت مثلث از این فرمول بهدست میآید با یک بار جذر گرفتن از آن مساحت مثلث را خواهیم داشت. مرکز دایره محاطی محل برخورد نیمسازهای زوایای مثلث است. با دانستن خصوصیات بعضی از خطوط مانند ارتفاع یا عمود منصف و یا میانه میتوانیم به نتایج جالبی در مورد دست پیدا کنیم. برخی از این نتایج را بیان میکنیم: اگر بر سه ضلع مثلث خطوطی را عمود میکنیم به طوریکه این خطوط اضلاع را نصف نمایند.(در واقع عمود منصف اضلاع را رسم میکنیم)در این صورت محل برخورد این سه خط، مرکز دایرهای خواهد بود که مثلث را احاطه میکند . به این دایره، دایره محاطی گویند.این دایره طوری رسم میشود که از سه راس مثلث عبور کند. طبق قضیه فیثاغورث اگر مرکز دایره محاطی روی یکی از اضلاع قرار گیرد آنگاه زاویه مقابل آن ضلع قائم خواهد بود.به عبارتی دیگر مثلث ما قائم الزاویه خواهد بود. اگر مرکز دایره درون مثلث باشد، مثلث ما یک مثلث حاده خواهد بود و اگر بیرون مثلث باشد، مثلث از نوع منفرجه خواهد بود. ارتفاع مثلث خط راستی است که از یک راس مثلث عبور کرده و بر ضلع مقابل آن راس عمود میشود.ضلعی را که ارتفاع بر آن عمود است را قاعده مثلث گویند.طول ارتفاع، فاصله بین راس و قاعده نظیر ارتفاع است.اگر سه ارتفاع مثلث را رسم کنیم این سه ارتفاع همدیگر را در داخل مثلث قطع میکنند مگر در حالتی که مثلث، منفرجه باشد. محل برخورد نیمسازهای مثلث مرکز دایره محیطی است. [ویرایش] نیمسازهای مثلث نیمساز یک زاویه از مثلث خط راستی است که از یک راس مثلث گذشته و آن زاویه را به دو قسمت مساوی تقسیم کند. اگر نیمسازهای سه زاویه مثلث را رسم کنیم این خطوط در نقطهای درون مثلث همدیگر را قطع خواهند کرد.این نقطه مرکز دایره محاطی مثلث خواهد بود.این دایره درون مثلث قرار دارد به طوریکه اضلاع مثلث، خطوطی مماس بر دایره هستند. [ویرایش] میانههای مثلث میانه یک مثلث خط راستی است که ...
روش محاسبه سطح مثلث و اشکال هندسی
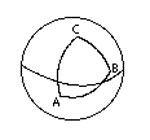
مثلث ار اساسی ترین اشکال در هندسه میباشد.یک مثلث دارای سه راس است که سه ضلع این رئوس را به هم وصل میکند.در هندسه اقلیدسی این اضلاع خطوطی مستقیم هستند. ولی در هندسه کروی این اضلاع کمان هایی از دایره عظیمه میباشند.این دو نوع مثلث را میتوانید در شکلهای روبرو مشاهده نمایید. انواع مثلثمثلث متساوی الاضلاع: مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای داخلی این مثلث نیز با هم برابرند.مثلث متساوی الساقین: مثلثی است که دارای دو ضلع با طولهای مساوی استو دو زاویه داخلی برابر دارد.البته مثلث میتواند دارای سه ضلع با طولهای مختلف و زوایای غیر مساوی باشد.مثلث قائم الزاویه: مثلثی را گویند که یکی از زوایای آن 90درجه باشد.نسبت های مثلثاتی مانند sin و cos ،بر روی مثلث قائم الزاویه تعریف میشوند.مثلث منفرجه: مثلثی را گویند که یکی از زوایای داخلی آن بیشتر از 90 درجه باشد.مثلث حاده : مثلثی را گویند که تمام زوایای داخلی آن کمتر از 90 درجه باشد.300 سال قبل از میلاد اقلیدس ،اصول اولیه درباره مثلث را ارائه داد.به عنوان مثال یکی از اصول مهم در مورد مثلث این است که مجموع زوایای داخلی یک مثلث برابر 180 درجه است. بر اساس این اصل میتوان با معلوم بودن دو زاویه از مثلث اندازه زاویه سوم را بدست آورد.یکی از مهمترین قضایای موجود در مثلثات قضیه فیثاغورث میباشد.در این قضیه رابطه بین وتر و اضلاع قائم یک مثلث قائم الزاویه بیان میشود. محاسبه مساحت مثلثبرای محاسبه مساحت یک مثلث روشهای مختلفی وجود داردو در ادامه به توضیح این روشها میپردازیم روش هندسیبرای محاسبه مساحت یک مثلث باید طول ارتفاع مثلث و نیز طول قاعده(ضلعی که ارتفاع بر آن عمود است) آن را داشته باشیم.آنگاه میتوانیم از فرمول زیر استفاده کنیم: در این فرمول b طول قاعده و h طول ارتفاع مثلث میباشد. در شکل زیر نحوه بدست آمدن این فرمول بیان شده است: تبدیل مثلث به یک متوازی الاضلاع که دو برابر مثلث مساحت دارد وسپس تبدیل متوازی الضلاع به یک مستطیلبرای پیدا کردن مساحت مثلث (قسمت سبز) ابتدا یک کپی از مثلث (قسمت آبی) را برداشته و آن را 180 درجه میچرخانیم و به مثلث اولیه متصل میکنیم تا یک متوازی الاضلاع بدست آید. با بریدن قسمتی از متوازی الاضلاع و متصل کردن آن به ضلع دیگر آن(همانند شکل) یک مستطیل ایجاد میشود. چون مساحت مستطیل برابر bh است .پس مساحت مثلث اولیه، نصف این مساحت خواهد بود.روش برداری محاسبه مساحت متوازی الاضلاع با استفادهاز ضرب خارجی دو بردارمساحت یک متوازی الاضلاع را میتوان با استفاده از بردارها محاسبه کرد.اگر AB,AC را مطابق شکل فرض کنیم آنگاه مساحت ABCD برابر |AB × AC| خواهد بود.این ...
محیط ومساحت اشکال هندسی( مثلث)
همه چیز درباره ی مثلث - چهار نوع مثلث داریم که شامل : مثلث متساوی الاضلاع - مثلث متساوی الساقین - مثلث قائمه الزاویه - مثلث مختلف الاضلاع ۲- در تمام مثلث ها مساحت ومحیط از یک قانون تبعیت می کند. ۳- مثلث قطر ندارد . ۴-مثلث مختلف الاضلاع خط تقارن ندارد. ۵- مثلث متساوی الاضلاع ۳ تا خط تقارن دارد به خاطراین که هر سه ضلعش باهم مساوی وبه یک اندازه هستند. ۶- مثلث متساوی الساقین یک تا خط تقارن دارد .به خاطراین که هر دو ساق های روبروباهم مساوی وبه یک اندازه هستند. ۷-هر مثلثی سه زاویه دارد که مجموع زوایای آن 180 درجه می باشد.<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" />
محاسبه مساحت در اشکال مختلف هندسی
۱)مساحت مـــربع = یـــک ضلع × خـــودش محیــط مـــربــــع = یک ضلع × ۴ ۲) مساحت مسـتطیـــــــل = طـول × عـرض محیط مستطیل = ( طول + عرض) × ۲ ۳) مساحت مثلث = ( قاعده × ارتــــــفاع ) ÷ ۲ محیط مثلث = مجموع سه ضلع ۴) مساحت مثلث متساوی الاضلاع = ( قاعده × ارتفاع ) ÷ ۲ محیط مثلث متساوی الاضلاع = یک ضلع × ۳ ۵) مساحت مثلث متساوی الساقین = ( قاعده × ارتفاع ) ÷ ۲ محیط مثلث متساوی الساقین= مجموع سه ضلع ۶) مساحت مثلث قائم الزاویه = ( قاعده × ارتفاع ) ÷ ۲ محیط مثلث قائم الزاویه = مجموع سه ضلع ۷) مساحت ذوزنقه = ( قاعده بزرگ + قاعده کوچک ) × ارتفاع ÷ ۲ محیط ذوزنقه = مجموع چهار ضلع ۸) مساحت لوزی = ( قطر بزرگ × قطر کوچک ) ÷ ۲ محیط لوزی = یک ضلع × ۴ ۹) مساحت متوازی الاضلاع = قاعده × ارتفاع محیط متوازی الاضلاع = مجموع دو ضلع متوالی × ۲ ۱۰) مساحت دایره = عدد پی ( ۳/۱۴ ) × شعاع × شعاع محیط دایره = عدد پی ( ۳/۱۴ ) × قطر ۱۱) مساحت بیضی = (نصف قطر بزرگ × نصف قطر کوچک ) × ۳/۱۴ ۱۲) محیط چند ضلعی منتظم = یک ضلع × تعداد اضلاعش ۱۳) حجم مکعب مستطیل = طـول × عـرض × ارتفاع حجم مکعب مربع = مساحت قاعده × ارتفاع ( طول یال×مساحت یک وجه) ۱۴) حجم هرم = مساحت قاعده ی هرم × ارتفاع هرم× یک سوم ۱۵)مساحت جانبی استوانه=محیط قاعده×ارتفاع . حجم استوانه =مساحت قاعده×ارتفاع سطح کل استوانه = سطح دو قاعده + مساحت جانبی ۱۶) مساحت جانبی منشور = مجموع مساحت سطوح جانبی مساحت کلی منشور = مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی ۱۷) حجم مخروط = مساحت قاعده × یک سوم × ارتفاع
فرمول محاسبه اشکال هندسی
فرمول محاسبه مساحت ومحیط اشکال هندسی نام شکل محیط مساحت تعداد خط تقارن تعداد قطر مربع اندازه یک ضلع × 4 اندازه یک ضلع × خودش 4 2 مستطیل (طول + عرض) × 2 طول × عرض 2 2 متوازی الاضلاع (مجموع 2 ضلع متوالی) × 2 قاعده × ارتفاع ندارد 2 ذوزنقه متساوی الساقین مجموع 4 ضلع(اضلاع) مجموع دو قاعده×ارتفاع تقسیم بر2 1 2 ذوزنقه قائم الزاویه مجموع 4 ضلع(اضلاع) مجموع دو قاعده×ارتفاع تقسیم بر2 ندارد 2 لوزی اندازه یک ضلع × 4 حاصلضرب دو قطر تقسیم بر 2 2 2 مثلث قائم الزاویه مجموع سه ضلع قاعده ×ارتفاع تقسیم بر 2 ندارد ندارد مثلث متساوی الساقین مجموع سه ضلع قاعده ×ارتفاع تقسیم بر 2 1 ندارد مثلث متساوی الاضلاع مجموع سه ضلع قاعده ×ارتفاع تقسیم بر 2 3 ندارد مثلث مختلف الاضلاع مجموع سه ضلع قاعده ×ارتفاع تقسیم بر 2 ندارد ندارد دایره قطر ×14/3 شعاع × شعاع × 14/3 بی شمار بی شمار
