محاسبه شعاع دایره
شعاع دایره محیطی و محاطی
محاسبه ی شعاع دایره ی محاطی مثلث: شعاع دایره ی محاطی مثلث را با حرف r نشان می دهیم .
دایره
دایره: (circle) مجموعه نقاطی از صفحه که فاصله ی آن از یک نقطه به نام مرکز برابر باشند ، دایره نامیده می شود. دایره ی c به مرکز o و شعاع R را با نماد نشان می دهیم . وتر دایره :(circle chord) پاره خطی که دو نقطه از محیط دایره را به هم وصل می کند . هر دایره بیشمار وتر دارد . مانند وتر های AB و CD در دایره ی C . قطر دایره:(circle axis) بزرگترین وتر در هر دایره را قطر می نامند . قطر وتر ی از دایره است که از مرکز می گذرد مانند قطر MN در دایره ی C. کمان دایره :(circlearc) قسمتی از محیط دایره را می گویند که به دو نقطه روی محیط دایره محدود شده باشد. اگر دو نقطه ی A و B را روی دایره C در نظر بگیریم دو کمان پدید می آید ، کمان کوچکتر را به صورت و کمان بزرگتر را به صورت می خوانیم . í نقطه و دایره : نقطه و دایره نسبت به هم 3 وضعیت دارند :1 نقطه داخل دایره است. 2 نقطه روی دایره است. 3 نقطه خارج دایره است . íوضع یک خط و یک دایره نسبت به هم: خط و دایره نسبت به هم سه حالت دارند: 1. خط خارج دایره است که در این صورت فاصله ی خط تا مرکز دایره از شعاع بزرگتر است. یعنی d 2.خط بر دایره مماس است.که در این صورت فاصله ی خط تا مرکز دایره با شعاع مساوی است . یعنی d = r 3.خط دایره را در دو نقطه قطع می کند که در این صورت فاصله ی خط تا مرکز دایره از شعاع کو چکتر است. یعنی: d < r íزاویه و دایره: زاویه ی مرکزی:زاویه ای که رأس آن مرکز دایره باشد زاویه ی مرکزی نامیده می شود. در شکل مقابل زاویه ی AOB یک زاویه مرکزی است و کمان AB کمان مقابل آن می باشد. نکته: اندازه ی زاویه ی مرکزی با کمان مقابلش مساوی است. زاویه ی محاطی: زاویه ی محاطی زاویه ای است که رأس آن روی دایره و اضلاع آن دو وتر از همان دایره باشند . در شکل مقابل زاویه ی یک زاویه ی محاطی است و کمان BC ، کمان مقابل آن می باشد. نکته :اندازه ی زاویه ی محاطی نصف کمان مقابل آن است. زاویه ی ظلّی : هر زاویه ای که رأسش روی دایره و یک ضلع آن وتری از دایره و ضلع دیگرش بر دایره مماس باشد ، زاویه ی ظّلی نامیده می شود. در شکل مقابل یک زاویه ی ظّلی و کمان AB کمان مقابل به زاویه ی ظّلی A می باشد. نکته : اندازه ی زاویه ی ظّلی نصف کمان مقابل آن است. íمثلث و دایره : دایره ی محاطی مثلث : 3 نیمساز زوایای داخلی مثلث یکدیگر را در یک نقطه مانند o قطع می کنند.می دانیم فاصله ی نقطه ی o از 3 ضلع مثلث به یک فاصله است (با توجه به مبحث تساوی مثلث ها)؛ یعنی اگر عمودی ها ی OK ،OH و OE را بر اضلاع مثلث فرود آوریم ،داریم : OE=OH=OK پس اگر دایره ای به مرکز O و شعاع OH رسم کنیم ، این دایره در K و H و E بر سه ضلع مثلث مماس خواهد بود . این دایره ، دایره ی محاطی مثلث نام دارد . مرکز دایره ی محاطی مثلث نقطه ی تلاقی ...
روش محاسبه سطح مثلث و اشکال هندسی
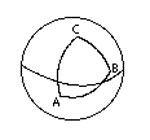
مثلث ار اساسی ترین اشکال در هندسه میباشد.یک مثلث دارای سه راس است که سه ضلع این رئوس را به هم وصل میکند.در هندسه اقلیدسی این اضلاع خطوطی مستقیم هستند. ولی در هندسه کروی این اضلاع کمان هایی از دایره عظیمه میباشند.این دو نوع مثلث را میتوانید در شکلهای روبرو مشاهده نمایید. انواع مثلثمثلث متساوی الاضلاع: مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای داخلی این مثلث نیز با هم برابرند.مثلث متساوی الساقین: مثلثی است که دارای دو ضلع با طولهای مساوی استو دو زاویه داخلی برابر دارد.البته مثلث میتواند دارای سه ضلع با طولهای مختلف و زوایای غیر مساوی باشد.مثلث قائم الزاویه: مثلثی را گویند که یکی از زوایای آن 90درجه باشد.نسبت های مثلثاتی مانند sin و cos ،بر روی مثلث قائم الزاویه تعریف میشوند.مثلث منفرجه: مثلثی را گویند که یکی از زوایای داخلی آن بیشتر از 90 درجه باشد.مثلث حاده : مثلثی را گویند که تمام زوایای داخلی آن کمتر از 90 درجه باشد.300 سال قبل از میلاد اقلیدس ،اصول اولیه درباره مثلث را ارائه داد.به عنوان مثال یکی از اصول مهم در مورد مثلث این است که مجموع زوایای داخلی یک مثلث برابر 180 درجه است. بر اساس این اصل میتوان با معلوم بودن دو زاویه از مثلث اندازه زاویه سوم را بدست آورد.یکی از مهمترین قضایای موجود در مثلثات قضیه فیثاغورث میباشد.در این قضیه رابطه بین وتر و اضلاع قائم یک مثلث قائم الزاویه بیان میشود. محاسبه مساحت مثلثبرای محاسبه مساحت یک مثلث روشهای مختلفی وجود داردو در ادامه به توضیح این روشها میپردازیم روش هندسیبرای محاسبه مساحت یک مثلث باید طول ارتفاع مثلث و نیز طول قاعده(ضلعی که ارتفاع بر آن عمود است) آن را داشته باشیم.آنگاه میتوانیم از فرمول زیر استفاده کنیم: در این فرمول b طول قاعده و h طول ارتفاع مثلث میباشد. در شکل زیر نحوه بدست آمدن این فرمول بیان شده است: تبدیل مثلث به یک متوازی الاضلاع که دو برابر مثلث مساحت دارد وسپس تبدیل متوازی الضلاع به یک مستطیلبرای پیدا کردن مساحت مثلث (قسمت سبز) ابتدا یک کپی از مثلث (قسمت آبی) را برداشته و آن را 180 درجه میچرخانیم و به مثلث اولیه متصل میکنیم تا یک متوازی الاضلاع بدست آید. با بریدن قسمتی از متوازی الاضلاع و متصل کردن آن به ضلع دیگر آن(همانند شکل) یک مستطیل ایجاد میشود. چون مساحت مستطیل برابر bh است .پس مساحت مثلث اولیه، نصف این مساحت خواهد بود.روش برداری محاسبه مساحت متوازی الاضلاع با استفادهاز ضرب خارجی دو بردارمساحت یک متوازی الاضلاع را میتوان با استفاده از بردارها محاسبه کرد.اگر AB,AC را مطابق شکل فرض کنیم آنگاه مساحت ABCD برابر |AB × AC| خواهد بود.این ...
تشابه دوشکل هندسی
تشابه تشابه به معنی به هم مانند بودن و به یکدیگر شبیه بودن می باشد. دو تصویر که از یک منظره تهیه شده اند ولی از لحاظ اندازه ها با هم تفاوت دارند, دو تصویر مشابهند. پانتوگراف نام وسیله ای است که برای رسم شکلهای متشابه از آن استفاده می شود. نماد تشابه: برای نمایش تشابه دو شکل از نماد ~ استفاده می شود. اگر شکل Aو'A متشابه باشند, می نویسیم:'A~A نسبت تشابه: عددی است که تغییرات بزرگی یا کوچکی اندازه های اضلاع دو شکل متشابه را نشان می دهد. این عدد همان نسبت اجزای متناظر در دو شکل متشابه می باشد. در تصویر بالا مشاهده می کنیم که هر یک از اضلاع شکل A دو برابر شده اند, عدد 2 یا را نسبت تشابه این دو شکل می گوییم. کاربردهای تشابه: نقشه هر مکان با آن مکان متشابه است. ماکت یک ساختمان با آن ساختمان متشابه است. مهندسین راه و ساختمان محاسبات لازم را برای ساختن یک مکان بروی ماکت آن انجام می دهند و پس از مشخص شدن تمامی جزئیات اقدام به ساخت آن می کنند. امروزه متخصصان علم شبیه سازی علوم پزشکی, در کشور عزیزمان ایران به پیشرفتهای قابل توجهی دست یافته اند به طوریکه بعضی از اعضای بدن انسان را در محیط های شبیه سازی شده, تولید می کنند. در علوم کامپیوتر نرم افزارهای طراحی شده قادرند تصاویر قدیمی را بازسازی کرده و در اندازه های مختلف و به تعداد دلخواه تکثیر کنند. در ریاضیات شرایط لازم برای تشابه دوچند ضلعی را بررسی کرده و سپس به کمک نسبت تشابه مقادیر نامعلوم را محاسبه می کنیم.تناسب اضلاع دو چند ضلعی متشابه به ما کمک می کند روابط زیبایی را در اشکال هندسی به دست آوریم این رابطه های مهم در شکل های هندسی هستند که به ایجاد یک نرم افزار, ایجاد یک محیط شبیه سازی شده, رسم نقشه یک مکان, ساخت دقیق یک ماکت ساختمان و ... کمک می کنند. تشابه دو n ضلعی: دو n ضلعی در صورتی متشابه اند که: 1- زاویه هایشان دو به دو مساوی باشند. 2- اضلاعشان متناسب باشند. مثال: دو مربع دلخواه متشابهند. اگر دو مستطیل دارای طول ها و عرض های متناسب باشند, متشابهند اگر زوایای نظیر دو لوزی مساوی باشند, متشابهند. تشابه دو مثلث 1- اگر دو زاویه از مثلثی با دو زاویه از مثلث دیگر متساوی باشند, آن دو مثلث متشابهند. 2- اگر دو ضلع از مثلثی با دو ضلع از مثلث دیگر متناسب و زاویه های بین آنها متساوی باشند, آن دو مثلث متشابهند. 3- اگر سه ضلع از مثلثی با سه ضلع از مثلث دیگر متناسب باشند آن دو مثلث متشابهند. شکلهای متشابه:ملاحضه کردیم که تشابه, طول پاره خطها را به یک نسبت بزرگ یا کوچک می کند, اما اندازه زاویه ها را تغییر نمی دهد. با نوشتن تناسب اضلاع دو شکل متشابه می توان ...
مساحت دایره
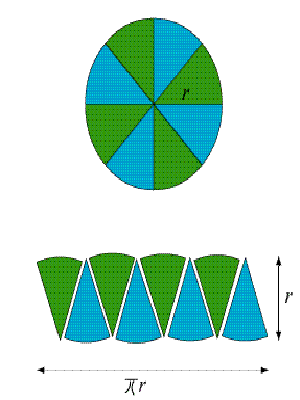
مساحت یک دایره از فرمول زیر محاسبه می شود. اما این فرمول از کجا آمده؟ بگذارید پیدا کنیم. کاری که می خواهیم انجام دهیم شکستن دایره به قسمتهای مساوی و بازآرائی آن به شکل مستطیل می باشد که مساحت آن را می دانیم. عرض × طول = مساحت ممکن است شما باور نکنید که می شود قطعات یک دایره را به مستطیل تبدیل کرد. خوب، فقط نگاه کنید ... آسان است. با دایره ای که می خواهیم بشکنیم شروع می کنیم. حالا دایره را به چهار قسمت مساوی تقسیم می کنیم. حالا آنها را طوری کنار هم می گذاریم تا یک مستطیل ایجاد شود. دقیقاً یک مستطیل نیست، هست؟ اما کار ما هنوز تمام نشده، بگذارید دایره را به هشت قسمت مساوی تقسیم کنیم. آنها را به شکل مستطیل مرتب می کنیم. مطمئناً شروع کرده که شبیه یک مستطیل بشود، اما هنوز تا آنجا فاصله داریم. قدم بعدی این است که به عقب برگردیم و دایره را به شانزده قسمت مساوی تقسیم کنیم. قطعات اینجا هستند. این دفعه وقتی آنها را کنار هم قرار می دهیم. خیلی بیشتر مثل مستطیل به نظر می رسند، ببینید. هدف ایجاد شکلی است که تا حد ممکن به مستطیل نزدیک باشد. تا بتوانیم مساحت آن را با استفاده از فرمول مستطیل محاسبه کنیم. عرض × طول = مساحت اما این شکل اضلاع صاف ندارد، بنابراین فرمول حیلی دقیق نمی باشد. بگذارید یک قدم جلوتر برویم و دایره راه به گروهی خرده های کوچک تقسیم کنیم. وقتی تمام قطعات را کنار هم قرار می دهیم، شکل مانند زیر به نظر می رسد. این خیلی شبیه یک مستطیل کامل است. اما می توانید ببینید که بالا و پائین هنوز کاملاً صاف نیستند. آنها کمی دست انداز دارند. می توانید تصور کنید که اگر باز هم به کارمان ادامه بدهیم چه اتفاقی خواهد افتاد؟ اگر به شکستن دایره به قطعات کوچکتر و کوچکتر ادامه دهیم؟ دست آخر، دست اندازها آنقدر کوچک می شوند که نمی توانیم آنها را ببینیم، و بالا و پائین شکل کاملاً مستقیم به نظر خواهند رسید. این چیزی است که خواهیم دید. یک مستطیل کامل. حالا تمام کاری که باید انجام دهیم پیدا کردن مساحت مستطیل با استفاده از فرمول عرض × طول = مساحت می باشد. سوال بعدی این است که، طول و عرض مستطیلی که از قطعات دایره ایجاد شده چه اندازه ای دارند؟ اجازه بدهید به عقب برگردیم، تا شما قطعات دایره را واضحتر ببینید. طول بیرونی دایره اصلی، مسافت پیرامون دایره، یا محیط دایره می باشد. نصف این مسافت پیرامون، در بالای مستطیل و نصف دیگر آن در پایین قرار می گیرد. به عبارت دیگر، تمام تکه های آبی و قرمز برابر محیط دایره می باشند. کناره های مستطیل درست شعاع هر ...
مثلث و دایره ، چند ضلعي منتظموچند نكته تكميلي
مثلث و دایره : دایره ی محاطی مثلث : 3 نیمساز زوایای داخلی مثلث یکدیگر را در یک نقطه مانند o قطع می کنند.می دانیم فاصله ی نقطه ی o از 3 ضلع مثلث به یک فاصله است ؛ یعنی اگر عمودی ها ی OK ،OH و OE را بر اضلاع مثلث فرود آوریم ،داریم : OE=OH=OK پس اگر دایره ای به مرکز O و شعاع OH رسم کنیم ، این دایره در K و H و E بر سه ضلع مثلث مماس خواهد بود . این دایره ، دایره ی محاطی مثلث نام دارد . مرکز دایره ی محاطی مثلث نقطه ی تلاقی نیمساز های زوایای داخلی آن است. محاسبه ی شعاع دایره ی محاطی مثلث: شعاع دایره ی محاطی مثلث را با حرف r نشان می دهیم . دایره ی محیطی مثلث: سه عمود منصف اضلاع یک مثلث بر یک نقطه مانند O می گذرند. می دانیم فاصله ی O از سه رأس مثلث به یک فاصله است، یعنی OA=OB=OC اگر به مرکز O و شعاع مثلأ OA دایره ای رسم کنیم این دایره بر دو رأس دیگر مثلث نیز عبور خواهد کرد . به این دایره ، دایره ی محیطی مثلث می گویند . مرکز دایره ی محیطی مثلث نقطه ی تقاطع عمود منصف های اضلاع آن است. محاسبه ی شعاع دایره ی محیطی مثلث: شعاع دایره ی محیطی مثلث را با حرف R نشان می دهند . در شکل زیر به دو مثلث توجه کنید ؛ این دو مثلث با هم متشابهند . تناسب اضلاع متناظر دو مثلث را می نویسیم: لذا در هر مثلث حاصل ضرب دو ضلع برابر است با : قطر دایره ی محیطی در ارتفاع وارد بر ضلع سوم یعنی : از طرفی می دانیم مساحت مثلث برابر است با : حالا با توجه به رابطه ی (1) و (2) می توان نوشت: دایره و چند ضلعی های متنظم : چند ضلعی متنظم:چند ضلعی که تمام اضلاع آن با هم و همه ی زاویه هایش نیز با هم مساوی باشند یک چند ضلعی متنظم نامیده می شود . مانند مربع که یک چهار ضلعی متنظم است. رسم چند ضلعی متنظم: برای رسم یک n ضلعی متنظم کافی است دایره ای را به n قسمت مساوی تقسیم کرده و نقاط تقسیم را به هم وصل کنیم . تقسیم دایره به n قسمت مساوی به صورت زیر انجام می شود: 1. یک زاویه ی مرکزی به اندازه ی رسم کنیم . 2.وتر نظیر این زاویه مرکزی را می کشیم . 3. پرگار را به اندازه ی این وتر باز کرده و پشت سر هم کمان های متوالی می زنیم تا دایره به n قسمت مساوی تقسیم شود . 1- در شکل مقابل زاویه ی از رابطه ی زیر بدست می آید . این زاویه از برخورد دو وتر دلخواه در داخل دایره بوجود آمده است. 2- در شکل مقابل زاویه ی از رابطه ی زیر بدست می آید . این زاویه از برخورد امتداد دو وتر دلخواه در خارج دایره بوجود آمده است. 3- در شکل مقابل زاویه ی از رابطه ی زیر بدست می آید : 4- 5- شعاع دایره ی محیطی مثلث متساوی الاضلاع دو برابر شعاع دایره ی محاطی آن مثلث است. 6- مرکز دایره ی محیطی مثلث قائم الزاویه وسط وتر و شعاع آن نصف وتر است. 7- ...
