محاسبه حجم استوانه
فرمول محاسبه حجم اشکال هندسی

یک ضلع × خودش = مساحت مربعیک ضلع × ۴ = محیط مربعطول × عرض = مساحت مستطیل۲× (طول + عرض) = محیط مستطیل۲ ÷ (قاعده × ارتفاع) = مساحت مثلثمجموع سه ضلع = محیط مثلثنصف ارتفاع × (قاعده بزرگ + قاعده کوچک) = مساحت ذوزنقهمجموع ۴ ضلع = محیط ذوزنقه۲÷ (قطر بزرگ × قطر کوچک) = مساحت لوزییک ضلع × ۴ = محیط لوزیارتفاع × قاعده = مساحت متوازی الاضلاعمجموع دو ضلع متوالی × ۲ = محیط متوازی الاضلاععدد پی × مجذور شعاع = مساحت دایره۱۴/۳ × شعاع × شعاع۱۴/۳ × قطر = محیط دایره مساحت کرهچهار ×عدد پی × مجذور شعاع = مساحت کرهحجم کره عدد پی × شعاع به توان ۳ = حجم کره۱۴/۳ × (نصف قطر کوچک × نصف قطر بزرگ) = مساحت بیضییک ضلع × تعداد اضلاع = محیط چند ضلعی منتظمطول یال × مساحت یک وجه = حجم مکعبارتفاع × عرض × طول = حجم مکعب مستطیلارتفاع × قاعده = حجم مکعبارتفاع هرم × مساحت قاعده هرم = حجم هرمارتفاع × مساحت قاعده = حجم استوانهارتفاع × محیط قاعده = مساحت جانبیسطح دو قاعده + مساحت جانبی = سطح کل استوانهمجموع مساحت سطوح جانبی = مساحت جانبی منشورمجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی = مساحت کلی منشورارتفاع × مساحت قاعده = حجم مخروط
روشي در محاسبه ي مساحت و حجم
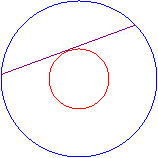
دراین مقاله هدف ،به دست آوردن مساحت وحجم چند شکل است اما نه با روش هایی که تا به حال دیده ایم ، بلکه راحت تر از آن !!! تعيين مساحت ناحيه ي حلقوي:براي تعيين مساحت يك ناحيه ي حلقوي(ناحیه ي بین دو دایره ي هم مرکز)، يك روش اين است كه اگر مساحت دو دايره را داشته باشيم، مساحت ناحيه ي حلقوي برابر تفاضل مساحت هاي دو دايره است. اما آيا روش ديگري براي تعيين مساحت ناحيه ي حلقوي شكل ، وجود دارد ؟اگر طول بزرگترين وتري كه ميتوان در اين ناحيه (ناحيه ي حلقوي شكل) رسم كرد را داشته باشيم، ميتوانيم مساحت این ناحیه را به دست آوريم.چون :«مساحت ناحيه ي حلقوي شكل برابر مساحت دايرهاي است كه قطرش برابر با بزرگترين وتري است كه ميتوان درداخل اين ناحيه رسم كرد.»ناحیه ي حلقوی شکل : مثال:اگر طول بزرگ ترین وتری که می توان درداخل یک ناحیه ي حلقوی رسم کرد ، برابربا 8 سانتی متر باشد ، مساحت این ناحیه ي حلقوی شکل برابر با مساحت دایره ای به قطر 8 سانتی متر می شود یعنی: سانتي متر مربع . تعيين حجم لوله و كره ي سوراخ شده :حال اگر بخواهيم حجم يك لوله ي استوانهاي شكل که دیواره ی ضخیمی دارد را به دست آوريم، (يعني حجم ناحيه ي بين دو استوانه را) طبق قسمت بالا با داشتن بزرگترين وتر در ناحيه ي حلقوی شکل ايجاد شده در قاعده ي استوانه ، ميتوان مساحت قاعده را به دست آورد و با داشتن ارتفاع لوله ، حجم محاسبه ميشود. به عنوان مثال:اگر طول بزرگ ترین وتر درناحیه ي حلقوی شکل قاعده ي لوله اي استوانه اي شكل را 8 سانتی متر بگیریم ، مساحت ناحیه ي حلقوی مانند مثال قبل برابر با: سانتي متر مربع می شود واگر ارتفاع لوله برابر با 10 سانتی متر باشد ، حجم لوله ي استوانه اي شکل برابر با : سانتي متر مكعب می شود . اگر داخل يك كره ي توپر،سوراخي استوانهاي شكل ايجاد كنيم كه مركزهاي دو قاعده ي استوانه و مركز كره بر يك استقامت باشند ، حجم شكل باقيمانده برابر است با حجم كرهاي به قطر طول سوراخ ايجاد شده در كره. به عنوان مثال اگر در يك كره ي توپر،سوراخي استوانهاي شكل به طول 6 سانتي متر با شرط فوق ايجاد كنيم ، حجم شكل باقيمانده برابر است با حجم كرهاي به قطر 6 سانتي متر يعني : سانتي متر مكعب . منبع: مجله ي گنجينه شماره ي 18
مساحت کل و جانبی و حجم استوانه
برنامه ای بنویسید که شعاع قاعده و ارتفاع یک استوانه را دریافت و مساحت جانبی، مساحت کل و حجم استوانه را محاسبه و چاپ کند.کدها و دستورات به صورت زیر مباشند:()Private Sub cmdExit_ClickEndEnd Sub-------------------------------------------------------()Private Sub cmdRun_ClickDim h As SingleDim r As Single("h = InputBox("ENTER A NUMBER("r = InputBox("ENTER A NUMBERDim j As Singlej = 3.14159 * r * h * 2Dim k As Single(k = 3.14159 * r * 2 * (r + hDim d As Singled = 3.14159 * r ^ 2 * hPrint Spc(2); "masahate janebi" & "=" & jPrint Spc(2); "masahate kol" & "=" & kPrint Spc(2); "hajm" & "=" & dEnd Sub-------------------------------------------------------برای دانلود کلیک کنید:http://s3.picofile.com/file/7668403652/ostovane.exe.html
مساحت ها ، محیط ها و حجم اشکال هندسی
۱) مساحت مـــربع = یـــک ضلع × خـــودش محیــط مـــربــــع = یک ضلع × ۴۲) مساحت مسـتطیـــــــل = طـول × عـرض محیط مستطیل = ( طول + عرض) × ۲۳) مساحت مثلث = ( قاعده × ارتــــــفاع ) ÷ ۲ محیط مثلث = مجموع سه ضلع۴) مساحت مثلث متساوی الاضلاع = ( قاعده × ارتفاع ) ÷ ۲ محیط مثلث متساوی الاضلاع = یک ضلع × ۳۵) مساحت مثلث متساوی الساقین = ( قاعده × ارتفاع ) ÷ ۲ محیط مثلث متساوی الساقین= مجموع سه ضلع۶) مساحت مثلث قائم الزاویه = ( قاعده × ارتفاع ) ÷ ۲ محیط مثلث قائم الزاویه = مجموع سه ضلع۷) مساحت ذوزنقه = ( قاعده بزرگ + قاعده کوچک ) × نصف ارتفاع محیط ذوزنقه = مجموع چهار ضلع۸) مساحت لوزی = ( قطر بزرگ × قطر کوچک ) ÷ ۲ محیط لوزی = یک ضلع × ۴۹) مساحت متوازی الاضلاع = قاعده × ارتفاع محیط متوازی الاضلاع = مجموع دو ضلع متوالی × ۲۱۰) مساحت دایره = عدد پی (3/14 ) × شعاع × شعاع محیط دایره = عدد پی ( 3/14 ) × قطر۱۱) مساحت کره = ۴ ×3/14 × شعاع به توان دو حجم کره = چهار سوم × 3/14 × شعاع به توان سه۱۲) مساحت بیضی = (نصف قطر بزرگ × نصف قطر کوچک ) ×3/14 ۱۳ ) محیط چند ضلعی منتظم = یک ضلع × تعداد اضلاعش۱۴ ) حجم مکعب مستطیل = طـول × عـرض × ارتفاع حجم مکعب مربع = قاعده × ارتفاع ( طول یال×مساحت یک وجه)۱۵ ) حجم هرم = مساحت قاعده ی هرم × ارتفاع هرم× یک سوم 16) مساحت جانبی استوانه = محیط قاعده × ارتفاع حجم استوانه = مساحتقاعده × ارتفاعسطح کل استوانه = سطح دو قاعده + مساحت جانبی ( مساحت مجموع دو قاعده + ارتفاع × پیرامون قاعده )۱۷) مساحت جانبی منشور = مجموع مساحت سطوح جانبی مساحت کلی منشور = مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی۱۸) حجم مخروط = مساحت قاعده × یک سوم × ارتفاع
(51) مخزن چقدر نفت دارد؟(+++)
مسئله ی هفته : مخزن چقدر نفت دارد؟ <?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" /> شکل بالا یک مخزن استوانه ای با مقطع بیضی را نشان میدهد که بصورت افقی بر روی زمین قرار گرفته است. ابعاد مخزن عبارت اند از: قطر بزرگ(2a)، قطر کوچک(2b) و طول مخزن(L). عمق مایع داخل مخزن هم h است. در شکل زیر سطح مقطع این مخزن نشان داده شده است:
روش محاسبه حجم اجسام هندسی
معرفی منشور 5 پهلو: í نام شکل: منشور 5 پهلو íیال های منشور: 'EE',DD',CC',BB',AA íوجه منشور: هر کدام از مستطیل های جانبی را یک وجه منشور می نامند. íارتفاع منشور: از آنجا که هر کدام از یال ها بر دو قاعده منشور عمود می باشند, لذا ارتفاع منشور با اندازه هر یک از یال ها برابر است. íقاعده ی منشور:منشور دو قاعده دارد. ABCDE و 'A'B'C'D'E که دو پنج ضلعی مساوی اند. رابطه های مهم: ارتفاع × مساحت قاعده =حجم منشور ارتفاع × محیط قاعده = مساحت جانبی منشور مساحت دو قاعده + مساحت جانبی = مساحت کل منشور استوانه:(Cylinder) نام شکلی است که دو قاعده دارد که دو دایره مساوی هستند و بر جانبی راست استوار است. اگر مستطیل را حول طول آن دوران دهیم, شکل فضایی حاصل استوانه نامیده می شود. در این صورت طول مستطیل ارتفاع استوانه و عرض آن شعاع قاعده استوانه می باشد. در شکل بالا مستطیل ABCD را حول طول آن دوران داده ایم و استوانه بوجود آمده است. رابطه های مهم: ارتفاع×مساحت قاعده(دایره) = حجم استوانه
ماشین حساب مثلث و هندسه
آسان به استفاده از ماشین حساب های آنلاین و هندسه solvers برای مباحث مختلف هندسه مانند محاسبه مساحت ، حجم ، فاصله ، نقطه تقاطع. این ممکن است مورد استفاده قرار گیرد برای بررسی پاسخ مشق شب ، تمرین و یا اکتشاف با ارزشهای مختلف برای فهم عمیق. ماشین حساب مثلث حق مثلث ماشین حساب و حل کننده. چهار آسان برای استفاده از ماشین حساب را برای حل مشکلات راست گوشه است که بسته به نوع اطلاعاتی در مورد مثلث به شما داده می شود. حل مثلث با توجه به رئوس آن است. ماشین حساب برای محاسبه هر سه زاویه و سه ضلع از مثلث. محیط و مساحت یک مثلث با توجه به رئوس آن است. ماشین حساب آنلاین برای محاسبه مساحت و محیط یک مثلث با توجه به مختصات رأس آن است. فرمول هران برای مساحت یک مثلث. محاسبه مساحت یک مثلث با استفاده از فرمول هران و هنگامی که سه ضلع یک مثلث هستند شناخته شده است. فرمول هران برای مساحت یک مثلث. هندسه ماشین حساب آنلاین برای محاسبه مساحت یک مثلث با استفاده از فرمول مثلثاتی ، هنگامی که دو ضلع و زاویه بین آنها شناخته شده (مورد جنسیت). مستطیل ها و مربعات بعدی مساحت ، محیط و قطر از مستطیل -- ماشین حساب. محاسبه مساحت ، محیط و مورب مستطیل داده از ابعاد آن (طول و عرض). طول و عرض مستطیل -- ماشین حساب. محاسبه ابعاد (طول و عرض) یک مستطیل با توجه به مساحت و فسفر از محیط مستطیل. مساحت مستطیل مورب ماشین حساب. ماشین حساب آنلاین برای محاسبه طول و عرض (ابعاد) یک مستطیل با توجه به مساحت و مورب. محیط مورب مستطیل ماشین حساب. ماشین حساب آنلاین برای محاسبه طول و عرض (ابعاد) یک مستطیل داده شده پیرامون آن و مورب. مساحت و محیط از میدان -- هندسه ماشین حساب. ماشین حساب آنلاین برای محاسبه مساحت و محیط یک مربع توجه به طول ضلع آن است. سطح مساحت و حجم ارقام بعدی 3D مساحت بیضی ماشین حساب. ماشین حساب آنلاین برای محاسبه مساحت بیضی داده محورهای نیمه آن است. بیضی جلد ماشین حساب. ماشین حساب آنلاین برای محاسبه حجم بیضی داده محورهای نیمه آن است. مساحت و حجم هرم -- هندسه ماشین حساب. ماشین حساب آنلاین برای محاسبه مساحت ، حجم و بسیاری از پارامترهای دیگر با توجه به ابعاد هرم از پایه آن مستطیل و ارتفاع آن است. مساحت و حجم مخروط راست -- هندسه ماشین حساب. محاسبه مساحت و حجم مخروط حق داده شود شعاع و ارتفاع آن است. مساحت و حجم استوانه راست -- هندسه ماشین حساب. محاسبه مساحت و حجم استوانه حق داده شود شعاع و ارتفاع آن است. مساحت و حجم هرم ناقص -- هندسه ماشین حساب. محاسبه مساحت ، حجم و پارامترهای دیگر از شعاع مخروط ناقص تحقیق خود را در پایگاه داده می شود ، تحقیق شعاع خود را در بالا و ارتفاع آن h. حجم و ...
محاسبه تغييرات در حجم موتور
(محاسبه تغييرات در حجم موتور) گنجايش يا حجم موتور جوهر و پايه موتورهاي تقويت شده است اين حجم ميزان فضاي اشغال شده سيلندر توسط پيستونها است كه هر كدام از آنها در يك كورس رو به پايين ( از نقطه مرگ بالا تا نقطه مرگ پايين ) اين حجم را به وجود مي آورند به ياد داشته باشيد اين مقدار جابجايي ، حجم كامل يك موتور نيست بلكه حجم كامل يك موتور ، مجموع گنجايش موتور در كورس پيستون و حجم محفظه احتراق است ، ولي در محاسبات معمولاً حجم اتاقك احتراق محاسبه نمي شود . حال حجم موتور را چگونه محاسبه مي كنند . براي محاسبه حجم موتور داشتن ميزان قطر پيستون الزاميست . قطر پيستون در اصل اندازه دهانه سيلندر است و كورس پيستون ، ميزان جابجايي پيستون از نقطه مرگ بالا تا نقطه مرگ پايين است . گرچه اين اندازه ها معمولاً از طرف كارخانه هاي سازنده اعلام مي شود ولي بعضاً اين ارقام تقريبي است و هنگام ساخت موتور كمي بالا و پايين مي شود حجم موتور را مي توان به روش زير محاسبه كرد : تعداد سيلندر * حجم استوانه سيلندر = حجم موتور يا به عبارتي تعداد سيلندر * كورس پيستون * مساحت سطح پيستون = حجم موتور پس داريم : 2( شعاع پيستون )*عدد پي = حجم موتورتعداد سیلندر*کورس پیستون* براي محاسبه حجم به ليتر بايد شعاع وكورس پيستون به سانتي متر داده شود و براي محاسبه به سي سي ( سانتيمتر مكعب ) بايد اعداد به ميليمتر و حاصل را به عدد يك هزار 1000 تقسيم كنيم . مثال : براي محاسبه حجم يك موتور 4 سيلندر با قطر پيستون 80 ميليمتر و كورس 23 ميليمتر داریم: حجم موتور روش دوم براي محاسبه حجم موتور عبارت است از: تعدا د سيلندر * كورس *2 ( قطر پيستون ) * ( عدد پي ) _______________________________4__ = حجم موتور 1000 با اين روش در مثال بالا داريم . اگر در روش دوم ، حاصل را به عدد 1000 تقسيم نكنيم ، از فرمول مي توان براي محاسبه حجم اتومبيلهاي آمريكايي كه به واحد اينچ مكعب محاسبه مي شوند استفاده نمود . براي مثال . براي محاسبه حجم موتور بيوك ايران با موتور 350 اينچ مكعبي و قطر پيستون 4 اينچي و كورس پيستوني معادل 3/4۸ اينچ داريم . كه با ذكر كردن عدد 350 اينچ مكعب بدست مي آيد . چند مثال : حال بياييد براي مثال با يك موتور 6 سيلندر سرو كار داشته باشيم . در موتورهاي نيسان ، سريz مي دانيم كه داتسون 240z بين سالهاي 1970 تا 1973 از قطر پيستون 83 ميلي متر و كورس 7/73 ميلي متر استفاده كرد كه با استفاده از فرمول داريم . كه بصورت ذكر شده مي شود 2393 سانتي متر مكعب . سپس در سال 1947 بعد از داتسون z240 موتور 260z آمد كه قطر پيستون آن همان 83 ميلي متر بود ولي كورس پيستون آن ...
محاسبه مساحت و محيط اشكال هندسي

نام شکل محیط مساحت تعداد خط تقارن تعداد قطر مربع اندازه ی یک ضلع × 4 اندازه ی یک ضلع × خودش 4 2 مستطیل 2 × ( طول + عرض ) اندازه ی طول × عرض 2 2 لوزی اندازه ی یک × 4 2 ( حاصل ضرب اندازه ی دو قطر ) 2 2 متوازی الاضلاع مجموع اندازه ی 4 ضلع اندازه ی قاعده × ارتفاع ندارد 2 ذوزنقه ی قائم الزاویه مجموع اندازه ی 4 ضلع 2 ÷ ( ارتفاع × مجموع دو قاعده ) ندارد 2 ذوزنقه ی متساوی الساقین مجموع 4 ضلع 2 ÷ ( ارتفاع × مجموع دو قاعده ) 1 2 ذوزنقه ی مختلف الاضلاع مجموع 4 ضلع 2 ÷ ( ارتفاع × مجموع دو قاعده ) ندارد 2 مثلث قائم الزاویه مجموع 3 ضلع 2 ÷ ( اندازه ی قاعده × ارتفاع ) ندارد ندارد مثلث متساوی الساقین مجموع 3 ضلع 2 ÷ ( اندازه ی قاعده × ارتفاع ) 1 ندارد مثلث متساوی الاضلاع مجموع 3 ضلع 2 ÷ ( اندازه ی قاعده × ارتفاع ) 3 ندارد مثلث مختلف الاضلاع مجموع 3 ضلع 2 ÷ ( اندازه ی قاعده × ارتفاع ) ندارد ندارد دایره 14/3 × اندازه ی قطر 14/3 × شعاع × شعاع بی نهایت بی نهایتفرمول های ریاضی اشكال هندسي : 2 ÷ (قاعده × ارتفاع) = مساحت مثلث مجموع سه ضلع = محیط مثلث نصف ارتفاع × (قاعده بزرگ + قاعده کوچک) = مساحت ذوزنقه مجموع 4 ضلع = محیط ذوزنقه 2÷ (قطر بزرگ × قطر کوچک) = مساحت لوزی یک ضلع × 4 = محیط لوزی ارتفاع × قاعده = مساحت متوازی الاضلاع مجموع دو ضلع متوالی × 2 = محیط متوازی الاضلاع 14/3 × شعاع × شعاع يا عدد پی × مجذور شعاع = مساحت دایره 14/3 × قطر = محیط دایره چهار ×عدد پی × مجذور شعاع = مساحت کره عدد پی × شعاع به توان 3 = حجم کره 14/3 × (نصف قطر کوچک × نصف قطر بزرگ) = مساحت بیضی یک ضلع × تعداد اضلاع = محیط چند ضلعی منتظم ارتفاع × مساحت قاعده = حجم مخروط طول یال × مساحت یک وجه = حجم مکعب ارتفاع × عرض × طول = حجم مکعب مستطیل ارتفاع × قاعده = حجم مکعب ارتفاع هرم × مساحت قاعده هرم = حجم هرم ارتفاع × مساحت قاعده = حجم استوانه ارتفاع × محیط قاعده = مساحت جانبی سطح دو قاعده + مساحت جانبی = سطح کل استوانه مجموع مساحت سطوح جانبی = مساحت جانبی منشور مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی = مساحت کلی منشور
آزمایشگاه(محاسبه چگالی اجسام با شکل نا منظم (کلید))
آزمایش چهار فعالیت صفحه ی 10 موضوع آزمایش: محاسبه چگالی اجسام با شکل نا منظم (کلید)
محاسبه حجم هوای بازدم
ندازه گیری هوای بازدموسایل لازم :بادکنک-یک عددنی -نوارچسب -بشر(لیوان)-تشتک شیشه ای (ظرف بزرگتریاکاسه ) -استوانه مدرجشرح فعالیت:بشر را کاملا پر از آب کرده درون تشتک شیشه ای قرارمی دهیم. یک بادکنک را چند بار باد می کنیم تا بدنه آن نرم شود. نی را وارد دهانه بادکنک می کنیم و با نوار چسب آن را محکم می کنیم، سپس یک نفس عمیق می کشیم تا جایی که با همان یک نفس بادکنک باد شود، دهانه نی را با دست محکم می گیریم تا هوای درون آن خارج نشود سپس آن را وارد بشر پر از آب می کنیم، دستمان را از دهانه نی برمی داریم، هوای درون بادکنک خارج شود و موجب سرازیر شدن آب می گردد. حجم آب سرازیر شده به درون تشتک را که با حجم هوای بازدم برابر است به کمک استوانه مدرج اندازه می گیریم.سیب زمینی شناور و غوطه ورسئوال صفحه 19 کتاب علوم هفتم بهتراست در کلاس انجام شود و نتایج به بحث گذاشته شود. در پایان فعالیت از دانش آموزان می پرسیم چکارکنیم که سیب زمینی در مرکز مایع قرارگیرد؟برای این کار باید مقداری آب تازه در لیوان آب نمک بریزیم بطوری که با آب نمک مخلوط نشود. برای این منظورمی توانیم یک قاشق بزرگ را بالای سطح آب نمک و مقابل دیواره لیوان قرار دهیم، آب تازه را ابتدا در قاشق بریزید و قاشق را به آرامی وارد آب نمک کنید حال قاشق را بردارید. در نتیجه با اضافه کردن مقداری آب سیب زمینی در مرکز مایع قرارمی گیرد.دراین آزمایش به جای سیب زمینی ازتخم مرغ هم می توانیم استفاده کنیم.
