مجموعه های ریاضی
مجموعه هاي اعداد
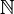
آشنایی با مجموعه های اعداد اعداد طبیعی، اعدادی هستند که برای شمردن به کار میروند. مجموعه اعداد طبیعی {... ,۳ ,۲ ,۱} است. در این مجموعه عدد صفر وجود ندارد و با اضافه کردن آن، مجموعه اعداد حسابی به وجود میآید. این مجموعه یک مجموعه نامتناهی است. در ریاضیات، مجموعه اعداد طبیعی را با نماد N یا نمایش میدهند. این حرف از آغاز واژه انگلیسی Natural، به معنای طبیعی، گرفته شده است. اعداد حسابی همان اعداد طبیعی هستند که صفر هم به آنها اضافه شده است. اعداد صحیح به مجموعه اعداد طبیعی مثبت و اعداد طبیعی منفی و عدد صفر گفته میشود. این مجموعه را در ریاضی معمولا با Z یا (ابتدای کلمه zahlen که در زبان آلمانی به معنی اعداد است) نشان میدهند. مجموعه اعداد صحیح، مانند مجموعه اعداد طبیعی، یک مجموعه شمارای نامتناهی ست. شاخهای از ریاضیات که به مطالعه اعداد صحیح می پردازد، نظریه اعداد نام دارد. اعداد گویا (یا به زبان دیگر، اعداد کسری) حاصل تقسیم دو عدد صحیح هستند، به شرطی که عدد دوم صفر نباشد. هر عدد گویا را به شکل a/b یا میتوان نوشت (که a و b اعداد صحیح اند). در ریاضیات مجموعه اعداد گویا را با نمایش میدهند. مجموعه اعداد گویا مجموعهای شمارا است. این مجموعه، همچنین، زیرمجموعهای چگال (dense) از مجموعهٔ اعداد حقیقی است. اعداد گنگ، یا اعداد اصم، اعدادی حقیقی هستند که گویا نباشند، یعنی نتوان آنها را به صورت کسری که صورت و مخرجش عدد صحیح باشند نوشت. مجموعه اعداد گنگ مجموعهای ناشمارا است. میدان تمام اعداد گویا و گنگ را اعداد حقیقی گویند و آن را با نمایش میدهند. اعداد حقیقی را میتوان با اضافه کردن عدد موهومی() بسط داد. اعدادی به فرم a + bi که در آن a و b هر دو عدد حقیقی هستند را اعداد مختلط مینامند.
مجموعه ها
مجموعه مجموعه، از بنداشتهای (اصول تعریفناپذیر) در ریاضیات است. به هر گردایه یا دستهٔ مشخص از اشیاء دو به دو متمایز گفته میشود. مفهوم مجموعه با وجود سادگی آن از مفاهیم پایهای ریاضی است. نظریه مجموعه در اواخر سده ۱۹ مطرح شد و اکنون یکی از بخشهای اصلی آموزش ریاضیات است. مجموعه گردایهای از اشیاء متمایز است. این اشیاء، عضوها یا عناصر مجموعه نامیده میشود. اعضای یک مجموعه ممکن است هر چیزی باشد. مثلاً اعداد، افراد، حروف الفبا، مجموعهای از حقایق مجموعههای دیگر و جز اینها، بنابر این منظور از اشیاء در تعریف مجموعه لزوماً اشیاء مادی نیست بلکه هر نهادی را هرچند انتزاعی و کاملاً ذهنی (همچون اعداد) میتوان در ریاضیات یک شیء دانست و گردایه آن اشیاء را مجموعهای دانست. معمولاً مجموعهها را با حروف بزرگ لاتین مانند A، B،C نشان میدهیم. دو مجموعه Aو B برابر هستند اگر اعضای آن یکسان باشند. تعریف هر مجموعه یک مجموعه را میتوان با عباراتی به شکل زیر تعریف کرد: Aمجموعه نخستین ۴ عدد طبیعی است. B مجموعهای است که اعضای آن رنگهای پرچم ایران است. همچنین میتوانیم اعضای مجموعه را میان دو کروشه قرار دهیم: {۱,۲,۳,۴} = C {سبز، سفید، قرمز} = D البته دو تعریف گوناگون؛ هر دو میتوانند نشان دهنده یک مجموعه باشند. مثلاً برای مجموعههایی که در بالا تعریف کردیم، Aو C یکسان هستند زیرا عناصرشان با هم برابر است (A=C). همچنین به طور مشابه B = D . توجه کنید که در یک مجموعه، جابه جایی عناصر و نوشتن اعضای تکراری تأثیری در خواص مجموعه ندارد. به عنوان مثال: {۱۱,۶}={۶,۱۱}={۶,۱۱,۶,۶} حال فرض کنید E مجموعه نخستین هزار عدد طبیعی باشد. برای نمایش چنین مجموعههای بزرگ (که تعداد اعضای آنها زیاد است)، نوشتن همه عناصر مجموعه غیرعملی است. بنابراین Eرا به طور خلاصه به این شکل نمایش میدهیم: {۱۰۰۰,...,۱,۲,۳} = E معمولاً این شکل نوشتن برای مجموعههایی به کار میرود که اعضای آن الگوی مشخصی را دنبال میکنند که برای همه واضح است. اما در مجموعههایی مانند{۴-,۳-,۰,...,۳۵۷ }=F به راحتی نمیتوان تشخیص داد که "F مجموعه نخستین ۲۰ عددی است که چهار واحد کمتر از مربع عدد دیگری ست". در چنین مواردی برای نمایش اعضای مجموعه از علائم ریاضی استفاده میکنیم: F={n^۲-۴: 0 <= n <= ۱۹} , nЄN یعنی: F مجموعه اعدادی به شکل n^۲-۴ است به طوریکه n به اعداد طبیعی بین ۰ و ۱۹ تعلق دارد. مطالب در ارتباط با مجموعهها نظریه مجموعهها زیر مجموعه نظریه طبیعی مجموعهها نظریه اصل موضوعی مجموعهها مجموعه نامتناهی مجموعه تهی مجموعه کراندار مجموعه توانی مجموعه مناسب رابطه یک به یکاجتماع ...
مجموعه (آموزش ریاضی)
ولی وقتی می گوییم اشیا منظور ما چیست؟ اگر درباره مجموعه ای از گلها صحبت می کنیم هر گل یک شی به حساب می آید . و اگر صحبت ما مربوط به مجموعه ای معین از اعداد است هر عدد یک شی ریاضی است . به مجموعه اعداد مقابل توجه کنید : این مجموعه مجموعه اعدادی را که مجذور کامل یک عدد یک رقمی هستند به ما نشان می دهد . برای نامگذاری هر مجموعه چنین متداول است که مجموعه را با یکی از حروف بزرگ لاتین مشخص می کنیم . واعضای مجموعه را داخل دو آکلاد {}قرار می دهیم . به طور مثال اگر مجموعه بالا را A بنامیم اعضای مجموعه را به این صورت می نویسیم : A={1,4,9,16,25,36,49,64,81 برای نشان دادن عضو مجموعه از نماد استفاده می کنیم . به طور مثال اگر بخواهیم نشان دهیم که عدد ۳۶ عضو مجموعه A می باشد . این طور می نویسیم و می خوانیم : ۳۶ عضو مجموعه A هست . و برای عضو نبودن از نماد استفاده می کنیم . به طور مثال برای مشخص کردن اینکه عدد ۲۴ در این مجموعه وجود ندارد . می نویسیم و می خوانیم : ۲۴ عضو مجموعه A نیست . مجموعه تهی ممکن است یک مجموعه هیچ عضوی نداشته باشد در این صورت چنین مجموعه ای را تهی می نامیم . به طور مثال مجموعه حروف الفبای فارسی که دارای چهار نقطه هستند یک مجموعه تهی است . به دلیل اینکه چنین مجموعه ای هیچ عضوی ندارد . مجموعه تهی را با نماد {} یا نمایش می دهیم مجموعه های مساوی دو مجموعه را وقتی مساوی گویند که علاوه بر اینکه اعضایش مساوی باشد هر عضو که در یکی از مجموعه ها هست .در مجموعه دیگری هم وجود داشته باشد . مانند : مجموعه های AوB A={3,5,7,9 و B={3,5,7,9 این دو مجموعه با هم مساویند و مجموعه A در واقع مجموعه B هست . حتی با جابه جایی اعضا مجموعه تغییر نمی کند . مجموعه های معادل دو مجموعه را در صورتی معادل گویند که تعداد اعضای آنها با هم برابر باشد . مانند مجموعه های AوB A={1,2,3,4 و B={a,d,g,s به دلیل اینکه هر یک از مجموعه ها چهار عضو دارند و تعداد عضوهای آنها با هم برابر است این دو مجموعه با هم معادلند . مجموعه تک عضوی : اگر مجموعه ای فقط یک عضو داشته باشد آنرا مجموعه تک عضوی می نامند . مجموعه تک عضوی را مجموعه یکانی هم می گویند . مجموعه ی متناهی : به مجموعه ای گفته می شود که دارای اعضای محدود باشد . یا تعداد اعضای آن با پایان باشد . مانند مجموعه اعداد طبیعی کمتر از 10 . نکته : مجموعه تهی را جزء مجموعه های متناهی در نظر می گیرند . مجموعه نا متناهی : مجموعه ای است که دارای اعضای نا محدود است . یا تعداد اعضای آن بی پایان است . مانند مجموعه اعداد طبیعی . {...,A={1,2,3,4,5 مجموعه های جدا از هم : وقتی که دو مجموعه عضو مشترکی نداشته باشند . آن دو مجموعه را جدا از هم می گویند . تذکر : یکی از خاصیت های ...
مجموعه ها و زیر مجموعه ها
با سلام و عرض معذرت از اینکه چند وقتی نبودم با تبریک به مناسبت شروع سال تحصیلی جدید و همینطور حلول ماه مبارک رمضان .ماهی که در آن می توانیم اندکی از گناهانمان را سبک کنیم.خدا انشاالله سعادت این توفیق را از ما نگیره. مجموعه و زیر مجموعه اغلب با مختصر مطالعه ای در ریاضیات . می توان فهمید که در بیان اکثر مفاهیم بنیادی ریاضی مانند : مفهوم اعداد / مفهوم تابع/ مفاهیم جبری و غیره به مجموعه ها نیازمندیم. مجموعه ها را معمولاْ تعریف نمی کنیم و آنچه هم به عنوان توصیف مجموعه بیان می شود ِ به خاطر نزدیک کردن ذهن به مفهوم مجموعه است. از نظر ریاضی یک مجموعه وقتی مشخص است که به ازای هر شئ در مجموعه یک جواب قطعی داشته باشد. چه ما آن جواب را بدانیم و چه ندانیم. مثلا" مجموعه ی اعداد اصم تعریف شده است و طبق تعریف امروزه می دانیم که عدد (پی) اصم است و هنوز هم اعدادی وجود دارد که اصم و یا گویا بودن آنها مشخص نیست . ولی قدر مسلم این است که این اعداد یا اصم هستند و یا نیستند. پس از مفاهیم عضویت و غیر عضویت در مجموعه ها به مفهوم زیر مجموعه ها توجهی خاص شده است که درسن دانش آموزان راهنمایی تفهیم آن اغلب سخت به نظر می رسد. ولی این مطلب را می توان با مثالهایی که مطرح می کنیم در حالتهای مختلف کاملا" برای دانش آموزان جا انداخت . مثلا" با در نظر گرفتن مجموعه ی A ( فرزندان یک خانواده ) و مجموعه B (پسران یک خانواده ) و مجموعه C (دختران یک خانواده )و از آنجا B, C را زیر مجموعه های A قرار دهیم چون هرپسر و هر دختری فرزند یک خانواده به حساب می آید . سپس با گسترش دادن مجموعه A در حد فامیلهای وابسته می توان زیر مجموعه های مختلف را آموزش داد . مثلا" با در نظر گرفتن اینکه خانواده ای فرزند ندارد به مجموعه ی تهی اشاره کرد.
.:: مجموعه ی اعداد حقیقی ::.
.:: مجموعه ی اعداد حقیقی ::. عدد حقیقی : (real number) حقیقی منسوب به حقیقت است و به معنی واقعی، اصلی و مقابل کلمه ی مجازی می باشد . در ریاضی هر یک از عددهای گویا و عددهای اصم را یک عدد حقیقی می نامند. مجموعه ی عدد های حقیقی: مجموعه ی تمام عددهای گویا و عددهای اصم را مجموعه اعداد حقیقی می نامیم و آنرا با حرف نمایش می دهیم. عدد اصم (گنگ): ir rational number = surd اصم به معنی کر و ناشنوا است و گنگ به کسی که کلمات را نتواند ادا کند. در ریاضی اگر عدد طبیعی n مجذور کامل نباشد ، آن گاه عددی اصم (گنگ) است. مانند می دانیم امکان نمایش این اعداد به صورت کسر وجود ندارد ،بنابراین «هر عدد حقیقی که گویا نباشد ، عدد اصم (گنگ) نامیده می شود.» محور عددهای حقیقی : برای نشان دادن یکسری عدد حقیقی روی محور از نمودار استوانه ای شکل استفاده می کنیم . قسمت های هاشور خورده و رنگ شده این نمودار اعضای مجموعه را نشان می دهد. مثال: نمایش هر یک از مجموعه های زیر را روی یک محور مشخص کنید. حل: تمامی عدد های حقیقی بین 2- و 3+ عضو این مجموعه هستند. دایره ی تو پر و علامت نشان می دهند که 2- عضو مجموعه ی A می باشد و دایره ی توخالی و علامت > نشان می دهند که 3 عضو مجموعه ی A نمی باشد. نکته: مجموعه ی A را به صورت (3 و 2-] نیز نشان می دهند که این مجموعه را بازه ی نیم باز 2- و 3 می گویند. حل: تمامی عدد های حقیقی بین 0و 4 عضو این مجموعه هستند. نکته:مجموعه ی B را به صورت (4 و 0)نیز نشان می دهند که این مجموعه را بازه ی باز 0 و 4 می گویند. حل: نکته:مجموعه ی C را به صورت[ 3 و 1-] نیز نشان می دهند که این مجموعه را بازه ی بسته 1- و 3 می گویند. حل: نکته:مجموعه ی D را به صورت (1 و ∞-) نیز نشان می دهند که این مجموعه بازه ای را نشان می دهد که از سمت راست محدود و از سمت چپ نامحدود است. (∞- را بخوانید: منفی بی نهایت) نمایش اعداد اَصَم (گنگ): فرض کنیم یک عدد اصم (گنگ) است ؛ جای تقریبی این عدد را می توان به کمک محاسبه ی جذر تقریبی روی محور مشخص کرد. مثال: عدد بین کدام دو عدد صحیح متوالی قرار دارد ؟ حل:مقدار تقریبی جذر 5 از عدد 2 بیشتر و از عدد 3 کمتر است ؛ یعنی : اختلاف عدد ی که بین 2 و 3 باشد با عدد 3 بین دو عدد صحیح متوالی صفر و یک قرار دارد . یعنی : برای مشخص کردن جای دقیق تری از روی محور به ترتیب زیر عمل می کنیم: الف: مثلث قائم الزاویه مناسبی که طول آن باشد را رسم می کنیم . ب: دهانه ی پر گار را به اندازه ی وتر این مثلث باز می کنیم و از مبدأ علامتی روی محور در جهت مثبت محور می زنیم. مثال: در شکل مقابل تعداد ی مثلث قائم الزاویه ...
مجموعه
تعریف دسته یا گروهی از اشیای کاملا مشخص که صریحا بتوان گفت شیء عضو مجموعه است یا خیر.مانند مجموعه ی گل ها. انواع مجموعه های اعداد اعدادحسابی W یا I ={0,1,2,...} اعداد طبیعی N={1,2,3,...} اعداد صحیح Z={...,-1,0,1,...} اعداد گویا Q'=هر عددی که بتوان آن را به صورت کسر نمایش داد (اعداد گنگ(اصم Q'=هر عددی که نتوان آن را به صورت کسر نمایش دادمجموعه ی ترکیبی از اعداد گویا و گنگ است.=Rاعداد حقیقی عضو یک مجموعه عضو یک مجموعه را با نماد∈∉ نمایش می دهند.جابجایی اعضای مجموعه و عضو تکراری عضوی اضافه محسوب نمی شود.مجموعه ای که عضوی نداشته باشد مجموعه ی تهی نامیده و آن را با علامت{} یا ϕنمایش می دهند. مثال: A={1,2,3 }_1∈A,2∈A,3∈A زیر مجموعه هر گاه همه عضو های مجموعه A در مجموعه B باشد آنگاه می توان گفت A زیر مجموعه B است. زیر مجموعه را با نماد⊂⊄ نمایش می دهند. مثال: B={1,2,3,4}⊂A={1,2,3,4,5,6,7} { {B={1,2,3,4,5}⊄A={1,5,8,2,3 مجموعه ی تهی زیر مجموعه ی همه ی مجموعه هاست.هر مجموعه ای زیر مجموعه ی خودش است.تعداد زیر مجموعه های یک مجموعه ی n عضوی از فرمول 2n به دست می آید. تعداد زیر مجموعه های m عضوی یک مجموعه n عضوی از رابطه ی زیر به دست می آید:n!÷(m! ×(n-m)!)زیر مجموعه ی محضبه یکی کمتر از تعداد زیرمجموعه های یک مجموعه گویند. مجموعه ی مرجعمجموعه ای را که شامل چند مجمموعه ی دیگر باشد را مجموعه ی مرجع می گویند و آن را با نماد M نمایش می دهند. اجتماع و اشتراک دو مجموعهاجتماع دو مجموعه به معنای تمامی اعضای دو مجوعه است و اعضای تکراری یک بار حساب می شوندکه آن را با نماد ∪نمایش می دهند.اما اشتراک دو مجموعه به معنای اعضای مشترک دو مجموعه است که یک بار حساب می شوند و آن را با نماد∩نشان می دهند. مثال: M 1 2 4 6 4 5 6 8 A 7 B که در این جا می توان گفت:4∈A,5∈B,6∈B,A∈M,B∈M A∩B={4,6},A∪B={1,2,4,5,6,8} متمم A یعنی چیز هایی که در A نیست ولی در مجموعه ی مرجع است. {A'={1,2,4,6,7چند نکته مهم: M'=ϕ ϕ'=M A∪A'=M A∩A'=ϕ M∪A=M M∩A=A: باشد آنگاه می توان گفتA⊂B اگرَA∩B=A ...
مجموعه تست های فصل صفر دیفرانسیل

مجموعه تست های فصل صفر دیفرانسیل حساب دیفرانسیل, سوالات تستی, عمومی by ریاضی سرا مجموعه تست های فصل صفر دیفرانسیل (مبحث ویژگی های اعداد) مجموعه تست های فصل صفر کتاب حساب دیفرانسیل و انتگرال (مبحث ویژگی اعداد) که توسط همکار تلاشگرمان جناب آقای حمید پوزن دبیر ریاضی دبیرستان های اهواز، به صورت پاورپوینت تهیه و جهت استفاده دانش آموزان و دبیران به سایت ریاضی سرا ارسال گردیده را در ادامه دانلود نمایید. با تشکر از استاد پوزن دانلود فایل پاورپوینت فصل صفر دیفرانسیل (مبحث ویژگی اعداد) فرمت فایل : powerpoint حجم فایل : ۶٫۶ مگابایت پسورد فایل: www.riazisara.ir منبع: ریاضی سرا
