فرق مشتق با دیفرانسیل
تانسورها
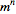
هر تانسور از مرتبه ی n در فضایی m- بعدی، ساختاری ریاضیاتی است که n شاخص و مولفه دارد که از قوانین تبدیلات مختصاتی پیروی می کند. هر شاخص تانسور، فقط مقادیری در محدوده ی تعداد بعدهای فضای تعریفی اختیار می کند. با این حال دخالت ابعاد فضایی تا حدود زیادی در معادلات تانسوری نامربوط به نظر می رسد. تانسورها نوع عمومی تر اسکالرها ( که فاقد شاخص هستند) ،بردارها (که تنها دارای یک شاخص اند) و نیز متریک ها (که فقط دو شاخص دارند) می باشند که می توانند تعداد دلخواه شاخص اختیار کنند. تانسورها بستر ریاضی مناسب و ساده ای را جهت فرمولبندی و حل مسائل متعدد در سیطره ی مباحث گوناگون فیزیک نظیر مکانیک سیالات و نسبیت عام فراهم می کنند. نمادگذاری هر تانسور عیناْ شبیه به یک ماتریس است، (مثل )، به جز اینکه یک تانسور مثلا ، ، قدرت انتخاب هر تعداد شاخص دلخواه را شامل هستند. بعلاوه، یک تانسور از مرتبه ی ،از نوع مختلط ـ شاخص یا به اصطلاح "مختلط" ، تلفیقی از شاخص بالا یا "پادوردا (contravariant)" و شاخص پایین "هم وردا (covariant)" می باشد. دقت کنید که مکان شاخص های پادوردا و هم وردا با یکدیگر فرق دارد که کوچکترین تفاوت میان جایدهی شاخص ها در یک تانسور چه در ترتیب و چه در بالا یا پایین بردن شاخص ها، منجر به ایجاد تانسور جدید و یا تغییر ساختمان ریاضی آن می گردد. برای مثال تانسور متمایز از شکل است. هنگامی که تانسور نسبت به تفاوت شاخص های پادوردا و هم وردا حساس باشد، تانسور حاصل از نوع عمومی خواهد بود. (در بحث ماتریس ها، یک ماتریس عمومی از جمع دو ماتریس پادمتقارن و متقارن به وجود می آمد که در اینجا نیز همین حالت برای تانسورها برقرار است). عدم تفاوت میان شاخص های هم وردا و پادوردا بیشتر در تانسورهای موردبحث در فضای اقلیدسی مانند تانسورهای دکارتی (Cartesian tensors) مطرح است. تانسورهای تبدیل شونده از مرتبه ی صفر، اسکالر (scalars) نامیده می شوند که همانند تانسورهای مرتبه ی ۱ یعنی بردارها (vectors) تبدیل می شوند. در نمادنویسی تانسوری، هر بردار به شکل نوشته می شود. به طوریکه i=1,...,m و ماتریس متناظر با آن گویای تانسوری از مرتبه ی (۱,۱) است که آن را به فرم می نویسیم. می توان عملیات جبری و دیفرانسیل را بر روی تانسورها انجام داد (مانند تانسورهای متریک (metric tensors) و تانسور جایگشت (permutation tensor) یا نماد دلتای کرونکر) که قابلیت تعریف پذیری عملگرهای تانسوری را دارا هستند. [مانند مشتق هم وردا (semicolon derivatives)]. با جابجایی شاخص های هم وردا و پادوردا می توان به عبارات و تانسورهای ساده تری دست یافت که این کار شامل بالابردن (index raising) یا پایین آوردن شاخص ها (index lowering) یا به عبارت ...
نمونه سوالات وجزوه ریاضی عمومی
آموزش ریاضی عمومی بطور تکمیلی همراه با توضیحتعبیر هندسی مشتق : مفهوم مشتق یک تابع را می توان شیب خط مماس بر نمودار تابع در آن نقطه تعبیر کردLim f(a+h) – f (a) => h شیب خط مماس بر نمودار f در نفطه x = a را با m(a) = f ´(a) نشان می دهیمشیب خط قائم ( عمود) بر نمودار با m´(a) نشان می دهیم m´= -1 m مثال : معادله خط مماس و قائم بر منحنی f(x) = x³ – 2x را در نقطه x = 1 بدست آوریدمشتق گیری ضمنی : توابعی که بصورت واضح بر حسب y = f(x) تعریف نمی شوند برای محاسبه مشتق از رابطه زیر استفاده می کنیم Y ´ = f ´(x) = - fx = x مشتق تابع نسبت به fy y مشتق تابع نسبت بهمثال : مشتق تابع زیر را بنویسیدF(x,y)=2x³ +xy² +y -3 = 0روش دوم مشتق گیری ضمنی :از همه جملات نسبت به x,y همزمان مشتق می گیریم سپس y ´ را بدست می آوریممثال :F(x,y)=2x³ +xy² +y -3 = 0مشتق تابع مرکب :هرگاه f,g توابع مشتق پذبر باشند مشتق تابع مرکب fog نسبت به x با فرض U = g(x) و y = fog (x) = f(u) به صورت زیر محاسبه می شود dy = df(u) × du dx du dxy = f(g(x) ) => y ´ = f ´(g(x) ) × g ´ (x)یک بار مشتق f را بدست می آوریم ، یک بار مشتق داخل پرانتز(x) مثال : اگر f (x) = √ x و g (x) = x² + 5x باشد مشتق fog = ؟روش حل مشتق fog : ابتدا f´(x) را حساب کرده بجای x های f ´ مقدار g را قرار می دهیم . سپس در فرمول ( fog (x) ) ´ = f ´(g (x))g ΄ (x) جایگزاری می کنیم g΄مشتق g استمثال : اگر f (x) = x³ مشتق تابع f (sin x) را حساب کنیدمشتق گیری پارامتری : X = f ( t ) معادلات را معادلات یرامتریث گویند ( یعنی بر حب t نوشته شده است ) y = g ( t )برای محاسبه dy ( همان مشتق ) در یک تابع پارامتری از روش زیر استفاده می کنیم dx dy dy = dt . dt dx dt مثال : در تابع y = t² + 5 مقدار dy را بدست آورید X = 2t + 1 dx قاعده زنجیره ای :اگر y = f ( u ) و u = g ( x) مشتق پذیر باشد آنگاه dy = df × du dx du dxمثال : f (u ) = 2u – 3u² + 7 و u = 2x³ - x + 5 df را حساب کنید dx قضایای مشتق :1- f (x) = secX → f΄ (x) = secx . tgx2- f (x) = cscX → f΄ (x) = - csex . cotx3- f (x) = sin X → f΄ (x) = . 1 . ...
سرفصل کنکور کارشناسی ارشد مهندسی کامپیوتر
زبان خارجه: مباحث بخش گرامر عبارتند از: زمان ها / افعال كمكي / مطابقت فاعل با فعل / كلمات ربطي / شبه جمله قيدي / جملات شرطي / صفت ها / جابجايي فاعل با فعل / حروف اضافه / وجه التزامي / معلوم و مجهول / الگوهاي فعل / شبه جمله صفتي / شبه جمله اسمي / اسامي قابل شمارش و غيرقابل شمارش بخش واژگان: این بخش به دایره لغات داوطلبان محدود است و هرچه لغات بیشتری بلد باشید در این بخش موفق تر خواهید بود.ریاضی مهندسی: سرفصل مطالب عبارتند از: سری فوریه ، انتگرال آن و تبدیل فوریه – تعریف سری فوریه – فرمول اولر – بسط در نیم دامنه – نوسانات واداشته انتگرال فوریه . معادلات با مشتقات جزئی: نخ مرتعش – معادله موج یک متغیره – روش تفکیک متغیرها- جواب دالامیر برای معادله موج – معادله انتشار گرما – موج – معادله موج دو متغیره – معادله لاپلاس در مختصات دکارتی و کروی و قطبی – معادلات بیضوی – پارابولیک و هیپربولیک – موارد استعمال تبدیل لاپلاس در حل معادلات با مشتقات جزئی – حل معادلات مشتق جزئی با استفاده از انتگرال فوریه . توابع تحلیلی و نگاشت کانفرمال و انتگرالهای مختلف : حد و پیوستگی – مشتق توابع مختلف – توابع نمائی و مثلثاتی – هذلولی و لگاریتمی – مثلثاتی معکوس و نمایی با نمای مختلف – نگاشت کانفرمال – نگاشت . انتگرال خط در صفحه مختلط – قضیه انتگرال کوشی – محاسبه انتگرال خط بوسیله انتگرالهای نامعین – فرمول کوشی – بسطهای تایلور و مک لورن – انتگرال گیری به روش مانده ها – قضیه مانده ها – محاسبه برخی از انتگرالهای حقیقی.محاسبات عددی: سرفصل مطالب عبارتند از: تعریف خطا – انواع خطا – انباشتگی خطا در محاسبات – ناپایداری در محاسبات – فرمول تکرار برای محاسبه توابع – روشهای حل معادلات غیر خطی شامل روشهای نصف کردن فاصله – رسم خطوط قاطع – رسم خطوط مماس – تکرار نقطه ثابت – اتیکن – فرمول خطا و اثبات همگرایی برای هریک از روشها – رتبه همگرائی – معادلات چند جمله ای (جداسازی – ریشه ها – حدود ریشه ها – روشهای حل ) – روش برستو برای تعیین رشته های موهومی – دستگاه معادلات خطی – روش های حل مستقیم (گاوس – ماتریس وارون ) – روشهای حل تکراری (سیدل) – روش نیوتن برای حل دستگاه معادلات غیر خطی –مقادیر ویژه – بردارهای ویژه – معادله مشخصه – روشهای فاکتورگیری – تفاضل های متناهی – روشهای درون یابی – برون یابی (نیوتن – گاوس – لاگرانژ – اتیکن – بسل ) – چند جمله ای چی شف – چند خمله ای Spline – درون یایب وارون – درون یابی دو متغیره – فرمول خطا – خمهای پوشا – روشهای حداقل مربعات – مشتق گیری عددی – تعیین نقاط اکسترمم توابع جدولی – ...
سرفصل مطالب به نقل از دانشجوی شریف
آمار:سرفصل مطالب : اشاره ای به تئوری مجموعه ها ، نمونه ها و نمایش جدولی آنها همراه با میانگین ، نما ، میانه ، واریانس و تبدیل و ترکیب احتمالات و قضایای مربوطه ، متغیرهای تصادفی و استقلال آنها ، واسطه و میانگین و واریانس توزیعات ، توزیعات دوجمله ای پوآسن ، فرق هندسی ، توزیع نرمال ، توزیع چند متغیر تصادفی ، نمونه گیری تصادفی و اعداد تصادفی ، نمونه گیری از جامعه کوچک ، برآورد پارامترهای آماری ، فواصل اطمینان ، آزمون ، آزمون فرضی تصمیم گیری ، تجزیه واریانس ، رگرسیون ، همبستگی ، آزمون روشهای ناپارامتری ، برازندن خط مستقیم براده ها ، توابع مولد گشتاور ، قضیه اعداد بزرگ ، قضیه حد مرکزی ، مجموع متغیرهای تصادفی مستقل ، احتمال شرطی ، قضیه احتمال کلی سرفصل مطالب : محاسبات عددی: سرفصل مطالب : تعریف خطا – انواع خطا – انباشتگی خطا در محاسبات – ناپایداری در محاسبات – فرمول تکرار برای محاسبه توابع – روشهای حل معادلات غیر خطی شامل روشهای نصف کردن فاصله – رسم خطوط قاطع – رسم خطوط مماس – تکرار نقطه ثابت – اتیکن – فرمول خطا و اثبات همگرایی برای هریک از روشها – رتبه همگرائی – معادلات چند جمله ای (جداسازی – ریشه ها – حدود ریشه ها – روشهای حل ) – روش برستو برای تعیین رشته های موهومی – دستگاه معادلات خطی – روش های حل مستقیم (گاوس – ماتریس وارون ) – روشهای حل تکراری (سیدل) – روش نیوتن برای حل دستگاه معادلات غیر خطی –مقادیر ویژه – بردارهای ویژه – معادله مشخصه – روشهای فاکتورگیری – تفاضل های متناهی – روشهای درون یابی – برون یابی (نیوتن – گاوس – لاگرانژ – اتیکن – بسل ) – چند جمله ای چی شف – چند خمله ای Spline – درون یایب وارون – درون یابی دو متغیره – فرمول خطا – خمهای پوشا – روشهای حداقل مربعات – مشتق گیری عددی – تعیین نقاط اکسترمم توابع جدولی – فرمول گاوس با نقاط محدود – انتگرال گیری عددی (ذوزنقه- سیمپسون – ابرگ – گاوس – لژاندر ) – فرمولهای خطا برای روشهای انتگرال گیری – انتگرال گیری چند گانه عددی – روشهای حل معادلات دیفرانسیل معمولی (تیلور – پیکارد – اویلر – هیون – اویلر بهبود یافته – رانگ (Runge) – کوتا(Kutta) – روشهای پیشگوئی و تصحیح جواب – فرمول خطا و حل معادلات دیفرانسیل با شرایط سرحدی – حل دستگاه معادلات دیفرانسیل . ساختمان داده: سرفصل مطالب : آرایه ها ، بردارها ، ماتریسها ، کاربرد ماتریسها MAZE ، ماتریسهای خلوت و کاربرد آنها ، پشته ها ، صفها و کاربرد آنها ، لیستها ، لیستهای پیوندی (خطی ، حلقه ای ، پیوند مضاعف، چند پیوندی) و کاربرد آنها ، تعاریف و اصول مقدماتی درختها ، درختهای دودویی ، نمایش و کاربرد (درختهای ...
تانسورها
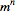
هر تانسور از مرتبه ی n در فضایی m- بعدی، ساختاری ریاضیاتی است که n شاخص و مولفه دارد که از قوانین تبدیلات مختصاتی پیروی می کند.
سرفصل کنکور کارشناسی ارشد مهندسی کامپیوتر

سرفصل کنکور کارشناسی ارشد مهندسی کامپیوترزبان خارجه:مباحث بخش گرامر عبارتند از:زمان ها / افعال كمكي / مطابقت فاعل با فعل / كلمات ربطي / شبه جمله قيدي / جملات شرطي / صفت ها / جابجايي فاعل با فعل / حروف اضافه / وجه التزامي / معلوم و مجهول / الگوهاي فعل / شبه جمله صفتي / شبه جمله اسمي / اسامي قابل شمارش و غيرقابل شمارش بخش واژگان:این بخش به دایره لغات داوطلبان محدود است و هرچه لغات بیشتری بلد باشید در این بخش موفق تر خواهید بود.ریاضی مهندسی:سرفصل مطالب عبارتند از:سری فوریه ، انتگرال آن و تبدیل فوریه – تعریف سری فوریه – فرمول اولر – بسط در نیم دامنه – نوسانات واداشته انتگرال فوریه .معادلات با مشتقات جزئی: نخ مرتعش – معادله موج یک متغیره – روش تفکیک متغیرها- جواب دالامیر برای معادله موج – معادله انتشار گرما – موج – معادله موج دو متغیره – معادله لاپلاس در مختصات دکارتی و کروی و قطبی – معادلات بیضوی – پارابولیک و هیپربولیک – موارد استعمال تبدیل لاپلاس در حل معادلات با مشتقات جزئی – حل معادلات مشتق جزئی با استفاده از انتگرال فوریه .توابع تحلیلی و نگاشت کانفرمال و انتگرالهای مختلف : حد و پیوستگی – مشتق توابع مختلف – توابع نمائی و مثلثاتی – هذلولی و لگاریتمی – مثلثاتی معکوس و نمایی با نمای مختلف – نگاشت کانفرمال – نگاشت .انتگرال خط در صفحه مختلط – قضیه انتگرال کوشی – محاسبه انتگرال خط بوسیله انتگرالهای نامعین – فرمول کوشی – بسطهای تایلور و مک لورن – انتگرال گیری به روش مانده ها – قضیه مانده ها – محاسبه برخی از انتگرالهای حقیقی.محاسبات عددی:سرفصل مطالب عبارتند از:تعریف خطا – انواع خطا – انباشتگی خطا در محاسبات – ناپایداری در محاسبات – فرمول تکرار برای محاسبه توابع – روشهای حل معادلات غیر خطی شامل روشهای نصف کردن فاصله – رسم خطوط قاطع – رسم خطوط مماس – تکرار نقطه ثابت – اتیکن – فرمول خطا و اثبات همگرایی برای هریک از روشها – رتبه همگرائی – معادلات چند جمله ای (جداسازی – ریشه ها – حدود ریشه ها – روشهای حل ) – روش برستو برای تعیین رشته های موهومی – دستگاه معادلات خطی – روش های حل مستقیم (گاوس – ماتریس وارون ) – روشهای حل تکراری (سیدل) – روش نیوتن برای حل دستگاه معادلات غیر خطی –مقادیر ویژه – بردارهای ویژه – معادله مشخصه – روشهای فاکتورگیری – تفاضل های متناهی – روشهای درون یابی – برون یابی (نیوتن – گاوس – لاگرانژ – اتیکن – بسل ) – چند جمله ای چی شف – چند خمله ای Spline – درون یایب وارون – درون یابی دو متغیره – فرمول خطا – خمهای پوشا – روشهای حداقل مربعات – مشتق گیری عددی – تعیین ...
رئوس مطالب مورد آزمون کنکور کارشناسی ارشد کامپیوتر
طراحی الگوریتم: سرفصل مطالب : یادآوری مطالب مهم در درس ساختمان داده و تکمیل نکات ارائه شده در خصوص : استقرا ریاضی و روشهای بازگشتی – پیچیدگی الگوریتمها و آنالیز آنها – نمادهای . روشهای حل مسأله : در هر روشی تعداد مسأله مهم انتخاب و الگوریتمهای هریک گفته شده و اثبات و آنالیز گردد. روش تقسیم و حل (مسائل: ماکزیمم و مینیمم یک آرایه . ضرب دو عدد n بیتی . روش Strassen در ضرب ماتریسها . تورنمنت بازیها . مرتب کردن بر اساس QuickSort . ) . روش برنامه سازی پویا (مسائل : ضرب ماتریسها – کوله پشتی – مثلث بندی بهینه یک چند ضلعی – طولانی ترین زیرترتیب مشترک – حروفچینی یک پاراگراف) . روش حریصانه (مسائل : مسائل زمانبندی – خرد کردن پول – کد هافمن ) . روشهای مبتنی بر جستجوی کامل و تکنیکهای محدود کردن فضای جستجو – استفاده از درخت بازی و (بازیهای Puzzle , tic-tac-tac ) . روشهای مکاشفه ای برای حل مسائل مشکل (مسأله فروشنده دوره گرد ) . الگوریتمهای گراف شامل : روشهای جستجوی گراف (عمقی و سطحی) . گرافهای بدون جهت (الگوریتمهای Dijkstra – درخت پوشای مینیمال – اجزاء همبند – کاملاً همبند و مسائل دیگر ) . گرافهای جهت دار (الگوریتمهای Floyd ، مرتب کردن Topologycal اجزا دو همبند و …) – شبکه های ماکزیم جریان و مسائل مربوطه . معماری کامپیوتر: سرفصل مطالب : تعریف معماری کامپیوتر – اشاره ای به تاریخچه کامپیوتر و نسلهای آن – معرفی واحدهای اصلی کامپیوتر – طراحی مجموعه دستورالعمل – بررسی معیارها و مسائل – نحوه اجرای دستورالعملها به کمک زبان توصیف سخت افزار (مثل RTL) – روشهای طراحی واحد کنترل به روش سیم بندی شده – ساختار واحد کنترل – کنترل انواع گذرگاه و مسیریابی داده – طراحی واحد حسابی – منطقی و محاسبه تأخیرها – طراحی واحد کنترل ریزبرنامه پذیر – حافظه و سلسله مراتب آن – حافظه های ایستا و پویا و معرفی حافظه نهان (Cache) و مجازی (Virtual) – الگوریتمهای حسابی جمع – تفریق – ضرب و تقسیم – الگوریتمهای ممیز شناور – شیوه های دسترسی به دستگاههای ورودی و خروجی (سرکشی – وقفه ) – دسترسی مستقیم به حافظه (DMA) و به اشتراک گذاری گذرگاه (BUS) – اشاره به روند توسعه معماری کامپیوتر و تفاوتهای CISC , RISC . سیستم عامل: سرفصل مطالب : تعریف سیستم عامل و وظایف اساسی آن به عنوان ماشین مجازی و مدیر منابع – انواع منابع – تاریخچه مختصر سیستم های عامل – طبقه بندی انواع سیستمهای عامل – سیستم عامل از دید کاربر – مفهوم پردازه (فرآیند) – کار – وظیفه – انواع کار (مقید به ورودی/خروجی و عملیات پردازشی – بررسی بافرینگ – محیط های چند برنامه ای – سیستمهای عامل اشتراک زمانی و محاوره ای – مدیریت پردازنده – زمان بندی ...
