ریاضی مهندسی سری فوریه

ریاضی مهندسی و سری فوریه

ریاضی مهندسی(به زبان لاتین) ریاضی مهندسی(به زبان لاتین) ریاضی مهندسی(به زبان لاتین) ریاضیات عالی مهندسی-ریاضی مهندسی پیشرفته(به زبان لاتین) ریاضی مهندسی پیشرفته(آقای دکتر کاظم قنبری) ریاضی مهندسی(آقای دکتر معتقدی) ریاضی مهندسی(آقای دکتر پوررضا) ریاضی مهندسی(آقای دکتر شیدفر) ریاضی مهندسی ریاضی مهندسی و لاپلاس(آقای دکتر سیاهی) جزوه سری فوریه مثال های حل شده از سری فوریه(به زبان لاتین) سری فوریه و سیستم های دیفرانسیل(به زبان لاتین) سری فوریه(به زبان لاتین) سری فوریه و تبدیل لاپلاس

حل سوال سری فوریه ریاضی مهندسی مهندس مهاجر
حل سوال سری فوریه ریاضی مهندسی استاد مهاجر با نرم افزار متلب ضرایبفوریه و سری فوریه ی تابع f(x)=x^2*e^ -xx بین -3 و +3 هستدست نویس حلشکردیم 8 تا انتگرال جز به جز باید برای اولی حل کنیدگرافش رو هم رسم کردیم وبرای 3 جمله و 35 و 110 جمله با تشکر برنامه نویسی این سوال توسط مهندس مسافر انجام شده است که نهایت تشکر را از ایشان دارم جواب این مسأله رو با یک فرضیاتی می‏نویسم.امیدوارم که خطایی نداشته باشه. فرض می‏‏کنم تابع بازگرد هست و دوره تناوبش رو 6 می‏گیرم. برای راحتی از دستور سری فوریه مختلط ضرایب رو حساب میکنم. انتگرالها رو به روش دستی و دقیق حساب می‏کنیم. با این فرضیات، تابعی می‏نویسیم که ضرایب پیشگفته رو محاسبه کنه: كد: <?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" /> function cn=fsccoef(n,L) a=1+i*n*pi/L; cn=-(L^2./a+2*L./a.^2+2./a.^3).*exp(-a*L)+(L^2./a-2*L./a.^2+2./a.^3).*exp(a*L); cn=cn/(2*L); توضیح: از کارگرهای درایه به درایه استفاده شده تا حجم برنامه‏نویس کم بشه و سرعتش هم کم نشه. روش انتگرالگیری خیلی ساده است، و از تعمیم یک روش که در کتاب توماس و بعضی کتابهای دیگه درس داده به دست میاد. این روش رو من حدود 10 سال پیش ابداع کردم و به خیلیها یاد دادم، اما هنوز وقت نکردم روشش رو روی کاغذ و برای دیگران توضیح بدم. اگه وقت پیدا کردم، می‏نویسمش. (مهندس مسافر)با استفاده از این تابع، تابع دیگری مینویسیم که مقادیر سری فوریه رو در یک سری از نقاط که بهش می‏دیم حساب کنه. كد: function y=fsvalv(x,n,L) cn=fsccoef(-n:n,L); nx=length(x); y=zeros(size(x)); for k=1:nx y(k)=cn*(exp(i*(-n:n)*pi*x(k)/L).'); end توضیح: بدون حلقه for هم می‏شه تابع رو نوشت. حالا برنامه‏ای می‏نویسیم که کاری رو که خواسته شده بود انجام بده: كد: % main L=3; x=linspace(-L,L,40); fe=x.^2.*exp(-x); f3=fsvalv(x,3,L); f35=fsvalv(x,35,L); f110=fsvalv(x,110,L); plot(x,fe,x,f3,':',x,f35,'--',x,f110,'.-') xlabel('x'),ylabel('f(x)'),title('Fourier Series Approximations') legend('x^2e^{-x}','3 terms FS approx',... '35 terms FS approx','110 terms FS approx',0) توضیح: این برنامه رو باید اجرا کنید و خروجی رو ببینید. باقی چیزهایی که گفته شده خیلی ساده هست، می‏تونید بهش اضافه کنید. فکر کنم کتاب در کتاب Mastering MATLAB با استفاده از FFT برنامه‏هایی نوشته شده که همین کار رو انجام می‏دن. البته تقریبی هستند، چون از FFT استفاده شده. حالا ديگه برنامه تكميله؛ تست كردم. شما هم اجرا كنيد و خروجيش رو ببينيد. اگه خواستید در مورد سری فوریه مطالعه کنید می‏تونید به ویکیپدیا مراجعه کنید. برای یاد گیری تخصصی متلب می تونین کتاب شگردهای عددی تالیف مهندس مهدی مسافر رو تهیه کنین در این کتاب مثالهای کاربردی زیادی در رابطه با مباحث مهندسی آورده شده است.
دانلود جزوه ریاضی مهندسی
جزوه ای تایپ شده و کامل از دروس ریاضیات همانطور که می دانید این درس اهمیت زیادی در کنکور ارشد دارد و در دکترا نیز به این درس اهمیت بسیار زیادی می دهند . سر فصل هایی که در این جزوه می خوانید : فصل اول معرفی معادلات دیفرانسیل و مشتقات جزئی مسَاله میله نوسان کننده معادلات PDE خواص اپراتور خطی معادله دیفرانسیل PDE همگن یا هموژن Homogenus شرایط اولیه یا مرزی رابطه مدول الاستیسیته (یانگ) مدل سازی شار حرارتی عبور از یک صفحه معادله انتقال حرارت بررسی شرایط مرزی در معادله انتقال حرارت معادلات لاپلاس تابع هارمونیک خواص اپراتور خطی معادله هذلولی یا Hyperbolic و بیضوی یا Ecllipite و سهمی یا Parabolic انواع معادلات لاپلاس بیان مختصات مسَاله دیریشله مسَاله لاپلاس نوع یا نیومن مسًاله ی لاپلاس نوع سوم کارترین به استوانه ای استوانه ای به کروی دکارتی به کروی کروی به استوانه ای کارتزین به کروی بیان معادله لاپلاس در مختصات استوانه ای فصل دوم روش جداسازی متغیرها جواب مسَاله انتقالی حرارت با شرایط اولیه روش های دیگر حل معادلات PDE فصل سوم سری های فوریه معرفی توابع قطعه ای پیوسته سری کسینوسی فوریه بسط سری سینوسی خواص ضرایب سری فوریه قضیه پارسوال مشتق پذیری و انتگرال بسط فوریه استنتاج برای فضای توابع روش کلی فوریه برای بسط توسط توابع ارتونرمال انواع دیگر ارتوگونالیستی ضرب داخلی هرمتیک انتگرال فوریه معرفی توابع بسل و کاربردهای آﻧﻬا خاصیت تابع بسل (خواص توابع بسل) انتگرال کوشی قضیه کوشی مفهوم انتگرال انواع انتگرال حل معادله لژاندر ---------------------------------------------------حجم فایل: 627KB ---------------------------------------------------لینک دانلود پسورد فایل www.techno-electro.com میباشد.
سری فوریه

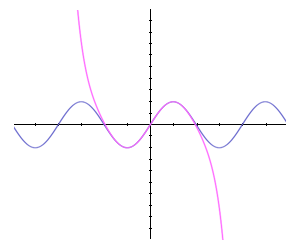
سری مثلثاتی یا فوریه توسعه نظریه سریهای مثلثاتی در 1822 ،با چاپ کتابی توسط فوریه آغاز شد.تحقیقات چندین ساله وی به گسترش نظریه وسیعی در مورد سریها منجر شدکه امروزه به نام خود وی معروف ،و از اهمیت بسیاری در ریاضیات ،علوم و فن برخوردار است.ایده اساسی این نظریه،معرفی توابع تناوبی یا دوره ای توسط توابع تناوبی(مثلثاتی) خاص است. سری فوریه برای بررسی حرکات تناوبی در آگوستیک یا صوت شناسی،الکترو دینامیک ،ایتیک یا نور شناسی، ترمودینامیک و غیره مورد استفاده قرار گرفته است. در مهندسی الکتریک مسائلی چون رفتار بسامدی ،عناصر سوئیچینگ ،یا انتقال ضربه ها را میتوان به کمک سری فوریه حل کرد. پیش بینی جزرومد در دریانوردی دارای اهمیت فراوانی است.از آنجا که اینها پدیده هایی تناوبی هستند از سری فوریه استفاده میشود و در تمام بندرهای مهم،وسائل مکانیکی چون پیش بینی کننده های جزر و مد ساخته میشود.امروزه کمتر شاخه‌ای از فیزیک،ریاضیات، یا صنعت و فن وجود دارد که در آن از سریهای فوریه استفاده نشود. تعریف سری توابع که جمله عمومی آن با ضرایب ثابت و است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و تابع تناوبی ی را نشان میدهد. این تابع لزوما پیوسته نیست، و در واقع اغلب بین آنچه که توسط فرمول های مختلف داده شده است گسستگی هایی دارد. از طرف دیگر،اگر این سری به طور یکنواخت همگرا باشد،آنگاه مجموع آن، ،پیوسته است. در این حالت میتوان ارتباطی بین ضرایب و و تابع مجموع به دست آورد.ضرب سری در عاملهای کراندار یا که در آنها p عدد صحیح و نامنفی است اختلالی در همگرایی یکنواخت آن به وجود نمی آورد،بنابراین میتوان و را با استفاده از انتگرالگیری جمله به جمله سری یا محاسبه کرد.این انتگرالگیری ها شامل انتگرال های روی بازه توابع و و و اند. سری فوریه ، روشی در ریاضیات می‌باشد که به وسیله آن ، هر تابع متناوبی به صورت جمعی از توابع سینوس و کسینوس می‌تواند نوشته شود. نام این قضیه به اسم ریاضیدان فرانسوی ، ژوزف فوریه ،ثبت شده است. در نظریه سریهای فوریه نشان داده شده است که اگر (f(x در شرایطی مثل (شرط دیریشله) صدق کند، می‌توان آن را به صورت سری هماهنگی به شکل: بسط داد و اینکه در نقاط ناپیوستگی سری سمت راست رابطه فوق برابر مقدار متوسط است. ضرایب an و bn را می‌توان با استفاده از روابط متعامد:که در آنها mnδ نماد کرونکر است که به ازای m=n برابر واحد و در غیر اینصورت صفر است. همچنین اگر یک تابع متناوب با تناوب T باشد یا به عبارتی: (f(t + T) = f(t آنگاه ، ...
سری فوریه در متلب
محاسبه ی ضرایب فوریه با استفاده از انتگرال عددی بسیار وقتگیر است. در نتیجه ما مجبور هستیم به دنبال متدهایی باشیم که با بکارگیری درونیابی توابع چند جمله ای مثلثاتی از میان داده هایی با فواصل یکسان، محاسبات را به انجام برساند.فرمولهای نتیجه شده اساس یک الگوریتم مهم است که تبدیل سریع فوریه خوانده می شود .(fft). اگرچه ضرایب فوریه که از طریق میان یابی حاصل می شوند تقریبی هستند،اما این ضرایب برای حالاتی که تعداد نقاط نمونه توانی از 2 باشد به سرعت قابل محاسبه می باشند. در ادامه درباره ی ایده ی پشت روش درون یابی مثلثاتی میان فواصل یکسان بحث میشود. دانلود آموزش سری فوریه در متلب ( پی دی اف - 11 صفحه )
محاسبه سری فوریه به صورت عددی

قبلا درمورد محاسبه سری فوریه به کمک جعبه ابزار تحلیلی (symbolic) توضیحاتی را داده بودم،امروز نحوه محاسبه سری فوریه به صورت عددی را توضیح می‌دهم. سری فوریه به شکل‌های گوناگون قابل تعریف است، برای راحتی کار فرم ساده زیر را در بازه‌ی 0< t < 1 را در نظر بگیرید و ضرایب سری فوریه را می توان به این صورت تعریف کرد اگر در این قسمت مشکلی دارید به کتابهای ریاضی مهندسی مراجعه کنید. فرض کنید برای محاسبه‌ی سری فوریه تنها باید ضرایب آن را حساب کرد، برای محاسبه هرکدام از ضرایب یابدهرکدام از انتگرال‌های فوق را حساب کنیم. برای نمونه من مقدار an را حساب می کنم functiony = anfunc(t) y = 2*sin(2*pi*t).*sin(2*n*pi*t); همانطور می دانید هرکدام از این ضرایب یک دنباله از اعدادهستند و با توجه به مقدار n مقدار آنها تغییر می کند. برای محاسبه‌ی تغییرات anfuncبا n 2 راه وجود دارد (مبحث مربوط به ParameterizingFunctions Called by Function Functions را در راهنمای متلبمطالعه کنید). من از تابع تودرتو (nested function) استفاده می‌کنم. functionmyfunc forn = 1:10 an(n) = quad(@anfunc,0,1); end an function y = anfunc(t) y = 2*sin(2*pi*t).*sin(2*n*pi*t); end end در ادامهکافی است که ابتدا دیگر ضرایب را حساب کردهو سپس مقدار سری را از جمع کردن آنها محاسبه کنیم.
سر فصل مطالب درسهای کارشناسی ارشد مهندسی کامپیوتر(ریاضی مهندسی)
ریاضی مهندسی:<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" /> سرفصل مطالب : سری فوریه ، انتگرال آن و تبدیل فوریه – تعریف سری فوریه – فرمول اولر – بسط در نیم دامنه – نوسانات واداشته انتگرال فوریه . معادلات با مشتقات جزئی: نخ مرتعش – معادله موج یك متغیره – روش تفكیك متغیرها- جواب دالامیر برای معادله موج – معادله انتشار گرما – موج – معادله موج دو متغیره – معادله لاپلاس در مختصات دكارتی و كروی و قطبی – معادلات بیضوی – پارابولیك و هیپربولیك – موارد استعمال تبدیل لاپلاس در حل معادلات با مشتقات جزئی – حل معادلات مشتق جزئی با استفاده از انتگرال فوریه . توابع تحلیلی و نگاشت كانفرمال و انتگرالهای مختلف : حد و پیوستگی – مشتق توابع مختلف – توابع نمائی و مثلثاتی – هذلولی و لگاریتمی – مثلثاتی معكوس و نمایی با نمای مختلف – نگاشت كانفرمال – نگاشت . انتگرال خط در صفحه مختلط – قضیه انتگرال كوشی – محاسبه انتگرال خط بوسیله انتگرالهای نامعین – فرمول كوشی – بسطهای تایلور و مك لورن – انتگرال گیری به روش مانده ها – قضیه مانده ها – محاسبه برخی از انتگرالهای حقیقی.
کاربرد سری فرویه

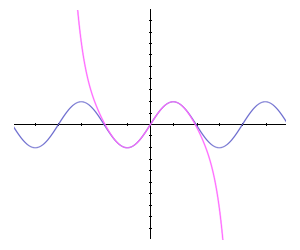
سری فوریه توسعه نظریه سریهای مثلثاتی در 1822 ،با چاپ کتابی توسط فوریه آغاز شد.تحقیقات چندین ساله وی به گسترش نظریه وسیعی در مورد سریها منجر شدکه امروزه به نام خود وی معروف ،و از اهمیت بسیاری در ریاضیات ،علوم و فن برخوردار است.ایده اساسی این نظریه،معرفی توابع تناوبی یا دوره ای توسط توابع تناوبی(مثلثاتی) خاص است. سری فوریه برای بررسی حرکات تناوبی در آکوستیک یا صوت شناسی،الکترودینامیک ،اپتیک یا نور شناسی، ترمودینامیک و غیره مورد استفاده قرار گرفته است. در مهندسی الکتریک مسائلی چون رفتار بسامدی ،عناصر سوئیچینگ ،یا انتقال ضربه ها را میتوان به کمک سری فوریه حل کرد. پیش بینی جزرومد در دریانوردی دارای اهمیت فراوانی است.از آنجا که اینها پدیده هایی تناوبی هستند از سری فوریه استفاده میشود و در تمام بندرهای مهم،وسائل مکانیکی چون پیش بینی کننده های جزر و مد ساخته میشود.امروزه کمتر شاخه‌ای از فیزیک،ریاضیات، یا صنعت و فن وجود دارد که در آن از سریهای فوریه استفاده نشود. تعریف سری توابع که جمله عمومی آن با ضرایب ثابت و است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و تابع تناوبی ی را نشان میدهد. این تابع لزوما پیوسته نیست، و در واقع اغلب بین آنچه که توسط فرمول های مختلف داده شده است گسستگی هایی دارد. از طرف دیگر،اگر این سری به طور یکنواخت همگرا باشد،آنگاه مجموع آن، ،پیوسته است. در این حالت میتوان ارتباطی بین ضرایب و و تابع مجموع به دست آورد.ضرب سری در عاملهای کراندار یا که در آنها p عددی صحیح و نامنفی است اختلالی در همگرایی یکنواخت آن به وجود نمی آورد،بنابراین میتوان و را با استفاده از انتگرالگیری جمله به جمله سری یا محاسبه کرد این انتگرالگیری ها شامل انتگرال های روی بازه توابع و و و اند.
دانلود رایگان کتاب سری فوریه و تبدیل لاپلاس

دانلود رایگان کتاب سری فوریه و تبدیل لاپلاس نام کتاب: سری فوریه و تبدیل لاپلاس نام نویسنده: پل بنیچو - روزان بنیچو - نوربرت بوی - ژان پیر پوژهنام مترجم: محمود تقی زاده منظری - مهرداد تقی زاده منظری زبان: فارسی تعداد صفحه: 166 فرمت: PDF دانلود رایگان کتاب سری فوریه و تبدیل لاپلاس. این کتاب جامع و کامل، و در 2 فصل سریهای فوریه (فصل اول) و تبدیلات لاپلاس (فصل دوم) گردآوری شده است. دانلود رایگان