رنگ امیزی اعداد
اعداد رمزی
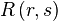
اعداد در قضیهٔ رمزی ( و بسط یافتهٔ آنها در موارد با بیش از دو رنگ) تحت عنوان اعداد رمزی شناخته میشوند. یک حد بالا برای را، میتوان از اثبات قضیه استخراج کرد و سایر استدلالها نیز حد پایین برای آن ارائه میکنند.(نخستین حد پایین توسط Paul Erdős با استفاده از روش احتمالاتی به دست آمد.) هر چند شکاف بزرگی میان مقادیر حد پایین و حد بالا وجود دارد. من تبع آن تعداد بسیار اندکی از r وsها هستند که ما برای آنها مقدار دقیق را میدانیم.محاسبهٔ حد پایین L برای معمولاً نیازمند ارائهٔ یک رنگ آمیزی گراف با دو رنگ قرمز و آبی است به طوری که هیچ زیرگراف آبی و هیچ زیرگراف قرمز در آن یافت نشود. هر چند که بررسی حالتهای مختلف رنگ آمیزی گراف با افزایش مقدار n از نظر محاسباتی بسیار پیچیده خواهد شد. تعداد حالتهای رنگ آمیزی رشدی بالاتر از رشد نمایی(exponentially) دارد.در حال حاضر حتی مقدار دقیق شناخته شدهاست هر چند که از قبل میدانستیم که مقدار آن بین 43(توسط Geoffrey Exoo) و 49 (Brendan McKay، وStanisław Radziszowski) قرار دارد. احتمال داده میشود که مقدار دقیق برای همیشه مجهول بماند. Paul Erdős میگوید:" بیگانگانی( نیروهای خارجی) را تصور کنید که بسیار نیرومندتر از ما بر روی زمین هستند و از ما خواستهاند که مقدار را محاسبه کنیم و در غیر این صورت سیارهٔ ما را نابود خواهند کرد. در این حالت ما باید تمام کامپیوترها و ریاضی دان هایمان را به کار بگیریم و برای یافتن مقدار مورد نظر به شدت تلاش کنیم. حال به جای این تصور کنید که از ما خواسته شده تا مقدار را محاسبه نماییم، در این وضعیت ما باید تمام تلاشمان را برای نابود کردن بیگانگان به کار ببریم!"مقدار برای مقادیر r و s تا 10 در جدول زیر نشان داده شدهاست. از آن جایی که در بسیاری از موارد مقدار دقیق را نمیدانیم، بهترین حدود یافت شده در جدول به نماش گذاشته شدهاست. برای مقادیر r و s کوچک تر از 3 به صورت R(1,s) = 1و R(2,s) = s برای تمام مقادیرs داده شدهاست.r,s123456789101111111111121234567891031369141823283640–434149182536–4149–6156–8473–11592–149515142543–4958–8780–143101–216125–316144–4426161836–4158–87102–165113–298132–495169–780179–11717172349–6180–143113–298205–540217–1031241–1713289–28268182856–84101–216132–495217–1031282–1870317–35836090-3319193673–115125–316169–780241–1713317–3583565–6588581–126771011040–4392–149144–442179–1171289–28266090-331581–12677798–23556در جدول یک تقارن ناچیز در میان قطر نیز وجود دارد. جدول فوق از جدول بزرگ تری که توسط Stanisław Radziszowski تالیف شده، اقتباس شدهاست. در سال ۲۰۱۲ قضیه توسط Geoffrey Exoo اثبات شد.یک مثال از چندین رنگ : R(3,3,3) = 17 گراف Clebschیک عدد رمزی رنگارنگ یک عدد رمزی است که در آن برای رنگ آمیزی از 3 رنگ یا ...
فعالیت تکمیلی برای شناخت اعداد و رنگ ها
همان طور که می دانید بچه ها پیش از آن که مفهوم عددی و ترتیبی اعداد را بشناسند ، شکل ظاهری عدد را در پیش از دبستان شناسایی می کنند. شناخت شکل اعداد زمینه ای برای یادگیری مفاهیم بعدی عدد می شود لذا پیش از آموزش اعداد و یا در حین معرفی مفهوم عدد ، بد نیست از فعالیت های مکمل جهت تثبیت شکل اعداد استفاده کنیم.همچنین در دانش آموزان ناشنوا ، آشنایی با رنگ ها گرچه از آمادگی 1 آغاز می شود اما متاسفانه دانش اموزان رنگ ها را تا پایه های بالاتر (تا دوم دبستان و بالاتر ) به نام نمی شناسند و برای هر یک از رنگ ها اشاره ای بکار می برند.فعالیت زیر باعث می شود دانش آموز با شکل نوشتاری رنگ ها و انطباق آن با اعداد در حین رنگ آمیزی آشنا شود.برای دیدن تصاویر بیشتر روی تصاویر کلیک کنید.
قضیه رمزی(ramsey)
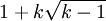
قضیه رمزی(ramsey) این مساله در باره رنگ آمیزی گراف هاست که در اینجا به حالت خاصی از آن اشاره میکنیم. برای اعداد صحیح و دلخواه k و l کوچک ترین عدد صحیح (r(k,l وجود دارد به طوری که هر گراف با این تعداد راس دارای خوشهای k راسی و یا شامل مجموعه مستقل l راسی است. مثال برای مثال(r(x,۲)=x r(۱,x)=۱ ۱=r(x,۱ r(۴٬۵)=۲۵ r(۵٬۳)=۱۴ r(۴٬۴)=۱۸ r(۳٬۴)=۹ r(۳٬۳)=۶ عدد رمزی آخر در سال ۱۹۹۳ با استفاده از کامپیوتر بدست آمده. تاریخچه این اعداد را برای اولین بار رمزی نام گذاری کرد وبعدها دانشمندان بزرگی چون گلیسون و گرینوودو اردوش بر روی آنها وقضایای مربوطه کار کردهاند این اعداد فعلا تجربی اند و جز در موارد خواص فرمولی برای آنها نداریم. برای آشنایی بیشتر به قضیه زیر توجه کنید. قضیه کران بالا در این جا میخواهیم کران بالایی برای اعداد رمزی (r(k,l بیان کنیم: اگر k>۱ , l>۱ آنگاه: (r(k,l) >= r(k,l-۱) + r(k-۱,l برهان: فرض کنید g گرافی با (r(k,l-۱) + r(k-۱,l راس باشد. راس v را در نظر بگیرید صبق اصل لانه کبوتری v یا به (r(k-۱,l راس وصل است ویا به (r(k,l-۱ راس وصل نیست. در صورتی که حالت اول بر قرار شود در این تعداد راس یا l راس مستقل اند ویا ۱-k راس خوشهاند واز آنجا که همه این رئوس به v وصل اند k-۱ راس به همراه k , v راس خوشه را تشکیل میدهند حکم مساله ثابت میشود. و اگر حالت دوم بر قرار شود یا k راس خوشه پیدا میشود و یا l-۱ راس مستقل. واز آنجا که v به این رئوس وصا نیست l-۱ راس و l,v راس مستقل را تشکیل میدهد. و حکم ثابت میشود. بیان مساله به صورت دیگر(حالت کلی): اگر q1,q2,...,qn اعداد صحیح بزرگتر از 2 باشند آنگاه عددی مانند (r(q1,q2,...,qn وجود دارد به طوری که اگر p بزرگتر از (r(q1,q2,...,qn باشد و یال های گراف را با n رنگ (رنگ های 1 تا n) رنگ کنیم ,به ازای حداقل یک رنگ مانند i زیر گراف کامل qi راسی وجود دارد که یال هایش هم رنگ رنگ i ام است. برای مثال r(3,3,3) = 17 حدس اردوس-فابر-لوواز (به انگلیسی: Erdős–Faber–Lovász conjecture) یک مسئله بسیار عمیق و مهم در بحث رنگ آمیزی گرافها در نظریه گرافها است. این نظریه بیان میکند که: اجتماع k کپی از k دسته که هر ۲ دستهٔ متمایز دلخواه حداکثر در یک راس اشتراک دارند دارای عدد رنگی k است. حداد و تاردیف در سال ۲۰۰۴ این نظریه را به بیان دیگری و با مطرح کردن یک مثال از کمیتههای موجود در دانشگاه ارایه کردند : فرض کنید در یک دانشکدهٔ دانشگاه k کمیـته وجود دارد و هر کـدام هم شامـل k نفر از اعضای هیئت علمی هستند و قرار است که همهٔ کمیتهها در یک اتاق با هم جلسه داشته باشند که در اتــاق k صندلی وجود دارد. همچنین فرض کنید که اشــتراک هر ۲ کمــیتهٔ متمایز دلخواه شامل ۱ نفر میشود. آیا ممکن است که اعضای ...
آموزش جمع اعداد با حاصل دو رقمی
1- تدریس با ابزار انگشتانهمان گونه که قبلاً آموزش داده اید ؛ دانش آموزان عددد6را به صورت (1 و 5 ) ؛ عدد 7 را به صورت ( 2 و 5 ) ؛ عدد8 را به صورت (3 و 5 )؛ عدد 9 را به صورت ( 4 و 5 ) اموخته اند.برای اینکه دانش آموزان را برای فرا گرفتن این نوع جمع ها آماده کنید باید قبل از آن تمرینی عملی با دانش آموزان داشته باشید.وآن اینکه دانش آموزان باید یاد بگیرند عدد 5 را که به عنوان مبنا فرا گرفته اند ؛ در ذهن مجرد خود نگهداری کنند . به دانش آموزان بگویید ،عدد 6 را با انگشتان دست نشان دهند .وقتی نشان دادند به آنها بگویید،بچه ها می خواهیم طور دیگر عمل کنیم وقتی عدد6 را می خواهیم نشان دهیم میتوانیم 5 آن را روی دوشمان (شانه-منظور ذهن مجرد) بگذاریم ،و1 آن را باانگشت نشان دهیم.« این کار را می توانید به صورت مجسم وبا چینه ها عملاً نشان دهید . چینه ی پنج تایی را روی شانه ی خود بگذارید و یک چینه ی دیگر را به طرف آن ببرید» بنابر این وقتی 1 انگشت دست را به طرف شانه می بریم ،یعنی 1 و آن 5 که روی شانه داریم. که همان 6 است.این تمرین را برای عدد های 7 و8 و 9 نیز انجام دهید. از دانش آموزان بخواهید این کار را چند بار انجام دهند.مثلاً 2 انگشت به طرف شانه ببرند وبگویند 7 . همین طور 3 انگشت به طرف شانه ببرند وبگویند 8 . 4 انگشت به طرف شانه ببرند وبگویند 9وقتی مطمئن شدید دانش آموزان یاد گرفتند تدریس را آغاز کنید.به دانش آموزان بگوییدبا یک دست عدد 6 را نشان دهند. دانش آموزان 1 انگشت را به طرف شانه می برند. سپس بگویید با دست دیگرعدد 8 را نشان دهند. دانش آموزان 3 انگشت خود را به طرف شانه می برند. حالا به بچه ها بگویید انگشتان دست خود را انتقال دهند.دانش آموزان 1 و3 را انتقال داده می شود 4بگویید پس بچه ها 5 تا روی این شانه داریم 5 تا هم روی آن شانه ، می شود 10 (1دسته ی ده تایی) و 4تا هم انگشتان دست که جمعاً می شوند 142- تدریس با چوب خطدانش آموزان عدد 6 را با چوب خط نشان دهند . سپس عدد 8 را نیز با چوب خط نشان دهند .به آنها طوری آموزش دهید که 3 تا چوب خط عدد 8 را کنار1 چوب خط عدد 6 بکشند . حالا دو تا چوب خط کامل دارند که می شود 10(1دسته ی ده تایی) با 4 تاچوب خط دیگر می شود 143- تدرس با محور اعداددانش آموزان 6 واحد را از نقطه ی صفر روی محور می شمارند وبه عدد 6 که رسیدند،یک کمان می زنند . سپس به دنبال آن 8 واحد می شمارند ، به عدد 14 می رسند ویک کمان دیگر می زنند . عدد 14 پاسخ جمع می باشد4- رنگ آمیزی با میله های ده تایی دو میله ی ده تایی روی تخته سیاه می کشیم . از دانش آموزی می خواهیم با گچ رنگی 6 خانه ی میله ی ده تایی را رنگ کند . به دنبال آن 8 خانه با رنگ دیگری رنگ کند. دانش آموز چهار ...
فعالیت تکمیلی برای شناخت اعداد و رنگ ها
همان طور که می دانید بچه ها پیش از آن که مفهوم عددی و ترتیبی اعداد را بشناسند ، شکل ظاهری عدد را در پیش از دبستان شناسایی می کنند. شناخت شکل اعداد زمینه ای برای یادگیری مفاهیم بعدی عدد می شود لذا پیش از آموزش اعداد و یا در حین معرفی مفهوم عدد ، بد نیست از فعالیت های مکمل جهت تثبیت شکل اعداد استفاده کنیم.همچنین در دانش آموزان ناشنوا ، آشنایی با رنگ ها گرچه از آمادگی 1 آغاز می شود اما متاسفانه دانش اموزان رنگ ها را تا پایه های بالاتر (تا دوم دبستان و بالاتر ) به نام نمی شناسند و برای هر یک از رنگ ها اشاره ای بکار می برند. فعالیت زیر باعث می شود دانش آموز با شکل نوشتاری رنگ ها و انطباق آن با اعداد در حین رنگ آمیزی آشنا شود.
آموزش ساخت برنامه رنگ آمیزی نقاشی با آدوب فلش ( یه شروع کلیدی )

سلامی دوباره ...پر انرژی و با انگیزه ! امروز قصد دارم یه شروع کلیدی داشته باشیم و در راهی قدم بزاریم که مرتبا پیشرفت خودمونو روز به روز احساس کنیم !حالا اگه پایه اید خودتونو جزو 100 نفر اول مشتاق به یادگیری و استفاده کلیدی ، آسان و شسته -رُِفته و واقعا مفید برنامه های مورد نیاز برای کلاس درس معرفی کنید .گامی بلند در مسیر حرفه ای کار کردن !حتما تا به حال برنامه های رنگ آمیزی مختلفی رو دیدین که به فرض دانش آموز از پالت رنگ یه رنگ رو انتخاب میکنه و بعد نقاشی های از قبل طراحی شده رو رنگ آمیزی میکنه ... از این نوع برنامه ها هم روی کامپیوتر و هم روی موبایل ها دیدین ... درسته ؟نمونه این نوع برنامه ها رو میتونید از آدرس زیر دانلود و مشاهده کنید :http://moralschool.mihanblog.com/post/126تا بحال به فکر این افتادید که خودتون هم میتونید از این نوع برنامه ها بسازید ؟ یا اینکه دوست داشتید چنین برنامه های جذابی رو خودتون با سلیقه و طرح های خودتون بسازید ؟حتی می تونید بجای نقاشی مثلا حروف الفبا و یا اعداد رو قرار بدید و از دانش آموزان بخواهید که حروفی رو که خونده رنگ آمیزی کنه و یا اعداد مورد نظر شما رو پیدا و رنگ کنه و به این شکل هم با رنگ ها در پایه های پایین تر بهتر و سریعتر آشنا بشن و هم دروس رو مخصوصا فارسی و ریاضی ، در پایه های اول و دوم با یادگیری عمیق تر بیاموزن ...تازه از این مهم تر استفاده از این برنامه ها برای یادگیری بهتر الگوهای رنگ آمیزی هست که فوق العاده میتونه به شما و دانش آموزان در این زمینه کمک کنه ! یعنی شما الگوهای کتاب رو یا الگوهای طراحی شده خودتونو با این برنامه آماده کنید و از دانش آموزان بخواهید که الگوها رو ادامه بدن و رنگ آمیزی کنن ! ببینید با کمی ابتکار به خرج دادن می تونید بصورت شگفت انگیزی یادگیری مطالب رو برای کلاس درس خودتون ساده تر کنید . پس این آموزش خیلی خیلی میتونه مفید باشه ولی خب کمی همت و تلاش هم میخواد ...اگه جزو اون دسته هستید که به این فکر افتادید و یا دوست داشتید ولی تا حالا سراغش نرفتید ، علاقه و آمادگی خودتونو اعلام کنید تا شروع کنیم !ولی این دفعه شرط آماده کردن و قرار دادن این آموزش رو این میزارم که حداقل 100 نفر بخصوص همکاران عزیز و دوستانی که میشناسم برای یادگیری پایه باشن پس زمانی دست بکار میشم که بدونم آمار علاقمندان و کسانی که حتما حتما شروع به کار میکنن به 100 مشتاق تولید محتوای آموزشی و مفید برای کلاس درس برسه !اون وقت بعد از تهیه آموزش ، رمز دریافت اونو به ایمیل و یا آدرس وبلاگی که معرفی می کنید ارسال خواهم کرد .پس من اینجوری منتظر می مونم >>> تا ببینم مستمع صاحب سخن رو به ذوق میاره ...
رنگآمیزی گراف

رنگآمیزی گراف : یک رنگامیزی گراف پترسن به کمک ۳ رنگ (کمترین تعداد رنگ ممکن). در نظریه گراف، رنگآمیزی گراف یکی از حالتهای خاص مسالههای برچسبگذاری گراف است. رویکرد کلی آن استفاده از نظیر کردن رنگهایی به یالها یا راسهاست که این رنگامیزی محدودیت خاصی را رعایت کند. در سادهترین حالت، رنگآمیزیای مورد نظر است که در آن هیچ دو راس مجاوری هم رنگ نباشند(رنگامیزی راسها). علاوه بر آن رنگامیزی یالها به همین صورت تعریف میشود. رنگامیزی گراف کاربردهای زیادی در زمینههای عملی و تئوری گوناگون دارد. علاوه بر مسالههای کلاسیک تعریف شده در این زمینه، با در نظر گرفتن محدودیتهای مختلفی روی نوع گرافها، روی روش رنگامیزی و حتی تعداد و رنگ عناصر گراف مسالههای متنوعی با کاربردهای وسیع در صنعت و علوم تعریف و حل میشود. با وجود اینکه این مساله از نظر علمی هنوز در حال رشد و بررسی بیشتر میباشد، با ظهور جدول سودوکو در بین عموم مردم شناخته و مشهور شدهاست. تاریخچه : یک رنگامیزی 4 رنگه نقشه ایالات متحده (بدون در نظر گرفتن آبها، کشورهای همسایه و متن نام ایالتها). اولین نتیجههای بدست آمده در مورد رنگامیزی گراف از تلاشهای انجام شده بر روی گرافهای مسطح برای حل مساله رنگامیزی نقشه بدست آمد. در آن زمان Francis Guthrie ادعا کرد که رنگامیزی نقشه ایالتهای مختلف بریتانیا روی نقشه، به طوری که هیچ دو ایالت مجاوری همرنگ نشوند، میتواند با ۴ رنگ انجام شود(شرط کافی). برادر Guthrie این مساله را برای معلم ریاضی خود Augustus de Morgan، در University College فرستاد. de Morgan، این مساله را در سال ۱۸۲۵ میلادی در نامهای که به William Hamilton نوشت مطرح کرد. در سال ۱۸۷۹ Arthur Cayley این مساله را در انجمن ریاضی شهر London مطرح کرد. در همان سال Alfred Kempe، نتایج بدست آمده را منتشر کرد و برای یک دهه تصور میشد این مساله حلشدهاست. برای تلاشهای Kempe در این زمینه او به عنوان یکی از اعضای جامعه سلطتنتی و بعدها به عنوان ریاست انجمن ریاضی شهر London انتخاب شد. در سال Heawood، ادعا کرد که استدلال Kempe اشتباه بودهاست و اثبات این مساله را برای ۵ رنگ منتشر کرد. در قرن معاصر او تلاشهای زیادی برای اثبات روشهای رنگامیزی نقشه با تعداد ۴ رنگ صورت گرفت که در نهایت در سال ۱۹۷۶ توسط Kenneth Appel وWolfgang Haken این مساله به کمک ایدههای خود Heawood و Kempe انجام شد که در آن زمان به دلیل استفاده از کامپیوتر برای اثبات مساله، شدیدا مورد قبول واقع نشد. رنگامیزی گراف از اوایل دهه ۷۰ به عنوان یک مساله الگوریتمی مورد بررسی قرار گرفتهاست، به طوری که جزء یکی از ۲۱ مساله NP-Complete که Karp معرفی کرد قرار ...
جمع اعداد یک رقمی با حاصل دو رقم در پایه ی اول
جمع اعداد یک رقمی با حاصل دو رقم در پایه ی اول برای مثال آموزش =8 + 6 1- تدریس با ابزار انگشتانهمان گونه که قبلاً آموزش داده اید ؛ دانش آموزان عددد6را به صورت (1 و 5 ) ؛ عدد 7 را به صورت ( 2 و 5 ) ؛ عدد8 را به صورت (3 و 5 )؛ عدد 9 را به صورت ( 4 و 5 ) اموخته اند. برای اینکه دانش آموزان را برای فرا گرفتن این نوع جمع ها آماده کنید باید قبل از آن تمرینی عملی با دانش آموزان داشته باشید.وآن اینکه دانش آموزان باید یاد بگیرند عدد 5 را که به عنوان مبنا فرا گرفته اند ؛ در ذهن مجرد خود نگهداری کنند . به دانش آموزان بگویید ،عدد 6 را با انگشتان دست نشان دهند .وقتی نشان دادند به آنها بگویید،بچه ها می خواهیم طور دیگر عمل کنیم وقتی عدد6 را می خواهیم نشان دهیم میتوانیم 5 آن را روی دوشمان (شانه-منظور ذهن مجرد) بگذاریم ،و1 آن را باانگشت نشان دهیم.« این کار را می توانید به صورت مجسم وبا چینه ها عملاً نشان دهید . چینه ی پنج تایی را روی شانه ی خود بگذارید و یک چینه ی دیگر را به طرف آن ببرید» بنابر این وقتی 1 انگشت دست را به طرف شانه می بریم ،یعنی 1 و آن 5 که روی شانه داریم. که همان 6 است. این تمرین را برای عدد های 7 و8 و 9 نیز انجام دهید. از دانش آموزان بخواهید این کار را چند بار انجام دهند.مثلاً 2 انگشت به طرف شانه ببرند وبگویند 7 . همین طور 3 انگشت به طرف شانه ببرند وبگویند 8 . 4 انگشت به طرف شانه ببرند وبگویند 9 وقتی مطمئن شدید دانش آموزان یاد گرفتند تدریس را آغاز کنید. به دانش آموزان بگوییدبا یک دست عدد 6 را نشان دهند. دانش آموزان 1 انگشت را به طرف شانه می برند. سپس بگویید با دست دیگرعدد 8 را نشان دهند. دانش آموزان 3 انگشت خود را به طرف شانه می برند. حالا به بچه ها بگویید انگشتان دست خود را انتقال دهند.دانش آموزان 1 و3 را انتقال داده می شود 4 بگویید پس بچه ها 5 تا روی این شانه داریم 5 تا هم روی آن شانه ، می شود 10 (1دسته ی ده تایی) و 4تا هم انگشتان دست که جمعاً می شوند 14 2- تدریس با چوب خط دانش آموزان عدد 6 را با چوب خط نشان دهند . سپس عدد 8 را نیز با چوب خط نشان دهند .به آنها طوری آموزش دهید که 3 تا چوب خط عدد 8 را کنار1 چوب خط عدد 6 بکشند . حالا دو تا چوب خط کامل دارند که می شود 10(1دسته ی ده تایی) با 4 تاچوب خط دیگر می شود 14 3- تدرس با محور اعداد دانش آموزان 6 واحد را از نقطه ی صفر روی محور می شمارند وبه عدد 6 که رسیدند،یک کمان می زنند . سپس به دنبال آن 8 واحد می شمارند ، به عدد 14 می رسند ویک کمان دیگر می زنند . عدد 14 پاسخ جمع می باشد 4- رنگ آمیزی با میله های ده تایی دو میله ی ده تایی روی تخته سیاه می کشیم . از دانش آموزی می خواهیم با گچ رنگی 6 خانه ی میله ی ده تایی را رنگ کند . به دنبال آن 8 خانه ...
