رسم تابع توزیع نرمال در مطلب

روش آزمون توزیع نرمال کولموگراف در SPSS
مطلب مصور زیر براحتی این روش را بهمراه آنالیز آماری آن توضیح می دهد: دو تصویر زیر بترتیب Box-Plot مرتبط با دو نمونه با توزیع نرمال و غیر نرمال است: حالا مستقیم به SPSS می رویم: در نرم افزار SPSS ورژن 17 ( در سایر ورژن های قبلی نیز با کمی تفاوت به همین شکل است ) ، ابتدا مطابق زیر به منوی Analyse و سپس به Descriptive Statistics و سپس به Explore می رویم و مراحل زیر را طی می کنیم که Command ( دستور ) Examine را برای ما اجرا می کند: سپس در تصویر زیر، متغیر مورد نظر را ( دراینجا a ) به جعبه Dependent List منتقل می کنیم. قسمت Display را به همان صورت گزینه از پیش انتخاب شده Both رها می کنیم و بر روی دکمه Plot کلیک می کنیم. این قسمت گزینه های مختلفی دارد که می توانید استفاده کنید ولی مهمترین چیزی که دراینجا منظورم است این است که حتما گزینه Normality Plots witht tests را تیک بزنید: نهایتا دکمه Continue را کلیک کرده و به صفحه قبلی که باز گشتید روی دکمه Ok کلیک می کنید. جدول زیر ، نمایش آنالیز توزیع نرمال به دو روش Kolmograph-Smirnov , و Shapiro-Wilk است که مشابه هم هستند ولی کاربرد متفاوتی در حجم نمونه های متفاوت دارند. ( تست کولموگراف معمولا برای داده های بالای 2000 عدد مناسب تر از تست شاپیرو است و البته هردو تست را می توان برای داده های کمتر از 2000 عدد استفاده کرد که بطور روتین از تست کولموگراف استفاده می کنیم و نتایج این دو تست معمولا تفاوتی در نتیجه نهایی نخواهد داشت مگر دربعضی شرایط خاص که توضیحش در این مبحث نمی گنجد: آنالیز آماری نتایج جدول تست کولموگراف در SPSS : داستان از اینجا حکایت می کند که در اصل با انجام تست کولموگراف ما داریم یک هایپوتز خنثی را که به شکل زیر است تست می کنیم: The distribution of the variable is Normal حالا با توجه به جدول فوق، به عدد متناظر با Sig. نگاه می کنیم. اگر این عدد کوچکتر از P مورد نظر ( معمولا P=0.05 ) باشد دراین صورت هایپوتز بالا را به نفع عدم توزیع نرمال متغیر مورد مطالعه رجکت می کنیم. ولی اگر مساوی یا بزرگتر از عدد P باشد ( همانطور که در بالا در تست کولموگراف برابر با 0.2 و در تست شاپیرو برابر با 0.691 است ) ، در این صورت هایپوتز خنثی بالا را قادر به رجکت کردن نیستیم ( به نفع نرمال بودن توزیع متغیر مورد نظر ) . بنابراین درصورتی که نتیجه جدول فوق را درمطالعه خود داشته باشید به این معنی است که متغیر مورد نظر از توزیع نرمال برخوردار است.

توزیع گاما

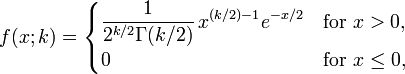
این توزیع حالت خاصی از توزیع گاما است تابع چگالی احتمال این هم شکل تابع چگالی احتمال است که Γ همانا مشخصات تابع گاما است تابع توزیع تجمعی کهدر تابع گاما دو تعریف داریم و همچنین در تعریف P(k,z) در توزیع گاما داریم مشخصه تابع کای دو شباهت با نرمال اگر که انگاه k متمایل است به نرمال بودن اگرچه این گرایش به کندی صورت می پزیرد چولگی ان به صورت است و درجه اوج ان در یک نمودار اماری (مد) بیشتر از 12 / k است و دو دگرگونی یا تغییر شکل که با اندیشه صحیح مطرح میشود که هر کدوم از این رهیافت های نرمال سریع تر از X که فیشر بطور غیر علمی ان را با نشان داده از روی ازمایش و کار البته! که تقریبا توزیع نرمال با میانگین و واریانس واحد است که ممکن است موفق بشود در تخمین نتیجه نرمال یکسان برای دیدن این مطلب چطوره که توجه کنید به میانگین و واریانس توزیع کایدو با با متغیر تصادفی که از ان داریم و که این نان دهنده تابع گاما است نسبت خاصی از تابع گاما در μz وقتی که این نسبت خاص را با فرمول زیر تخمین می زنیم و این به سادگی نشان می دهد که و دوباره این هم نشان می دهد که اقایان ویلسون و هیلتفلتری در سال ۱۹۳۱ نشان دادن که که تخمینی از توزیع نرمال با میانگین 1 − 2 / (9k) و واریانس 2 / (9k). که مقدار مورد انتظار از متغیر تصادفی دارای توزیع کایدو با k درجه آزادی و واریانس 2k و میانه با این راه تخمین زده میشود اطلاعاتی در مورد درگاشت (انتروپی ) که است رابطه توزیع ها توزیع نمایی است اگر داری توزیع کایدو است اگر برای اگر که دارای میانگین غیر صفر نشان دهنده توزیع غیر مرکزی از کایدو است توزیع کای دو با نوع خاصی از توزیع گاما با اگر که با و اگر که در جاییکه و مستقل و اگر که X داری توزیع کایدو باشه همانا دارای توزیع کایدو با تاخیر است توزیع تجمعی کایدو ویژگیها محدوده توزیع تابع مولد گشتاور برای پارامترها شانس موفقیت (حقیقی)‫گسترهتابع چگالی احتمالتابع توزیع تجمعی‫(سیدیاف)میانگینمیانهN/Aمُدواریانسچولگیکشیدگیانتروپی‫تابع مولد گشتاور (ام جی اف)تابع مشخصهتوزیع برنولی، توزیعی گسسته است که نام آن از نام دانشمند سوئیسی ژاکوب برنولی گرفته شده است.
صد نکته از آمار و احتمال مقدماتی
صد نکته از آمار و احتمال مقدماتی 1 هدف اصلی آمار انجام استنباط درباره جامعه وسنجش میزان عدم حتمیتی که در این استنباط ها وجود دارد. 2 خلاصه کردن و توضیح خصوصیات مهم مجموعه داده ها را آمار توصیفی می نامند. 3 نمودارهای نقطه ای را وقتی بکار می برند که تعداد مشاهدات نسبتا کم باشد(کمتر از 20 یا 25)و بافت نگار برای مواردی است که تعداد مشاهدات زیاد است......4 در تشکیل جدول توزیع فراوانی انتخاب تعداد رده ها از طریق آزمایش و خطا انجام می شود و بسته به تعداد داده ها بین 5 تا 15 تغییر می کند. 5 هیچگاه نباید برای نمایش داده های پیوسته از نمودار خطی استفاده کرد. 6 در نمایش بافت نگار اگر مستطیل ها در وسط دارای قله باشد آنگاه نمودار متقارن است ولی اگر مثلا سمت راست کشیده باشد چاوله به راست وبر عکس آن می شود چاوله به چپ. 7 هر معیار عددی که معرف مرکز مجموعه داده ها باشد معیار گرایش به مرکز است و از اصلی ترین آنها میانگین ومیانه است. 8 میانه نمونه ای:داده ها را بصورت مرتب و اگر تعداد داده ها(n) فرد باشد یک مقدار وسطی وجود دارد و در مورد nزوج که دو داده وسط وجود دارد متوسط آنها میانه است. 9 برای توزیع هائی که خیلی نامتقارن هستند میانه معیار معقولتری از میانگین است. 10 معمولا چارک ها را در مواردی که تعداد داده ها کمتر از 25 است محاسبه نمی کنند. 11 میانگین نمونه پیراسته:تمامی مشاهدات کمتر از چارک اول و بیشتر از چارک سوم را برمی داریم و میانگین باقی مشاهدات را حساب می کنیم. 12 میانگین نمونه وینزوری:به جای مشاهدات کمتر از چارک اول مقدار چارکک اول و به جای مشاهدات بزرگ تر از چارک سوم مقدار چارک سوم را قرار داده ومیانگین داده های حاصل را محاسبه می کنیم. 13 مهم ترین معیار های پراکندگی عبارتند از:واریانس وانحراف معیار 14 میانگین انحرافها همیشه صفر است. 15 در مقایسه دو مجموعه از داده ها بیشتر بودن s در یک مجموعه حاکی از وجود پراکندگی بیشتر در آن مجموعه داده ها نسبت به مجموعه دیگر است. 16 هدف قاعده چبیشف بین این مطلب است که هر فاصله ای به مرکز و به طول Yks شامل نسبت کمینه ای از داده هاست 17 دامنه را اغلب در مواردی که تعداد نمونه کمتر از 8 است بکار می برند. 18 در توزیع هائی که دارای دنباله کشیده در یک جهت هستند دامنه میان چارکی نمونه به عنوان معیار پراکندگی بر واریانس ترجیح داده می شود. 19 اگر بافت نگار دارای نمودار متقارن باشد هر دو معیار گرایش به مرکز میانگین ومیانه یکی هستند. 20 فضای نمونه ای گسسته شامل اعداد تکی ولی فضای نمونه ای پیوسته شامل بازه ای پیوسته است. 21 در مواردی که عناصر فضای نمونه ای دارای احنپتمال هم شانس هستند ، دارای ...
کل آمار مقدماتی در یک صفحه
۴ در تشکیل جدول توزیع فراوانی انتخاب تعداد رده ها از طریق آزمایش و خطا انجام می شود و بسته به تعداد داده ها بین 5 تا 15 تغییر می کند.۵ هیچگاه نباید برای نمایش داده های پیوسته از نمودار خطی استفاده کرد.6 در نمایش بافت نگار اگر مستطیل ها در وسط دارای قله باشد آنگاه نمودار متقارن است ولی اگر مثلا سمت راست کشیده باشد چاوله به راست وبر عکس آن می شود چاوله به چپ.7 هر معیار عددی که معرف مرکز مجموعه داده ها باشد معیار گرایش به مرکز است و از اصلی ترین آنها میانگین ومیانه است.8 میانه نمونه ای:داده ها را بصورت مرتب و اگر تعداد داده ها(n) فرد باشد یک مقدار وسطی وجود دارد و در مورد nزوج که دو داده وسط وجود دارد متوسط آنها میانه است.9 برای توزیع هائی که خیلی نامتقارن هستند میانه معیار معقولتری از میانگین است.10 معمولا چارک ها را در مواردی که تعداد داده ها کمتر از 25 است محاسبه نمی کنند.11 میانگین نمونه پیراسته:تمامی مشاهدات کمتر از چارک اول و بیشتر از چارک سوم را برمی داریم و میانگین باقی مشاهدات را حساب می کنیم.12 میانگین نمونه وینزوری:به جای مشاهدات کمتر از چارک اول مقدار چارکک اول و به جای مشاهدات بزرگ تر از چارک سوم مقدار چارک سوم را قرار داده ومیانگین داده های حاصل را محاسبه می کنیم.13 مهم ترین معیار های پراکندگی عبارتند از:واریانس وانحراف معیار14 میانگین انحرافها همیشه صفر است.15 در مقایسه دو مجموعه از داده ها بیشتر بودن s در یک مجموعه حاکی از وجود پراکندگی بیشتر در آن مجموعه داده ها نسبت به مجموعه دیگر است.16 هدف قاعده چبیشف بین این مطلب است که هر فاصله ای به مرکز و به طول Yks شامل نسبت کمینه ای از داده هاست17 دامنه را اغلب در مواردی که تعداد نمونه کمتر از 8 است بکار می برند.18 در توزیع هائی که دارای دنباله کشیده در یک جهت هستند دامنه میان چارکی نمونه به عنوان معیار پراکندگی بر واریانس ترجیح داده می شود.19 اگر بافت نگار دارای نمودار متقارن باشد هر دو معیار گرایش به مرکز میانگین ومیانه یکی هستند.20 فضای نمونه ای گسسته شامل اعداد تکی ولی فضای نمونه ای پیوسته شامل بازه ای پیوسته است.21 در مواردی که عناصر فضای نمونه ای دارای احنپتمال هم شانس هستند ، دارای مدل احتمال یکنواخت هستند.22 در اجتماع حداقل یکی از دو پیشامد رخ می دهد ولی در اشتراک باید هردو پیشامد رخ دهند.23 قاعده جایگشتها (ترتیب)زمانی که لازم است پیشامدی برحسب ترتیب مشخصی از نتایج بیان شود بکار می رود ولی در مورد ترکیب ،ترتیب رخ دادن مورد نظر نیست.24 اگر گزینش هرمجموعه به حجم n از جامعه N دارای احتمال یک بر باشد ، نمونه تصادفی نامیده می شود.25 بافت نگار احنمال برای ...
100 نکته آماری
1 هدف اصلی آمار انجام استنباط درباره جامعه وسنجش میزان عدم حتمیتی که در این استنباط ها وجود دارد. 2 خلاصه کردن و توضیح خصوصیات مهم مجموعه داده ها را آمار توصیفی می نامند. 3 نمودارهای نقطه ای را وقتی بکار می برند که تعداد مشاهدات نسبتا کم باشد(کمتر از 20 یا 25)و بافت نگار برای مواردی است که تعداد مشاهدات زیاد است. ۴ در تشکیل جدول توزیع فراوانی انتخاب تعداد رده ها از طریق آزمایش و خطا انجام می شود و بسته به تعداد داده ها بین 5 تا 15 تغییر می کند. ۵ هیچگاه نباید برای نمایش داده های پیوسته از نمودار خطی استفاده کرد. 6 در نمایش بافت نگار اگر مستطیل ها در وسط دارای قله باشد آنگاه نمودار متقارن است ولی اگر مثلا سمت راست کشیده باشد چاوله به راست وبر عکس آن می شود چاوله به چپ. 7 هر معیار عددی که معرف مرکز مجموعه داده ها باشد معیار گرایش به مرکز است و از اصلی ترین آنها میانگین ومیانه است. 8 میانه نمونه ای:داده ها را بصورت مرتب و اگر تعداد داده ها(n) فرد باشد یک مقدار وسطی وجود دارد و در مورد nزوج که دو داده وسط وجود دارد متوسط آنها میانه است. 9 برای توزیع هائی که خیلی نامتقارن هستند میانه معیار معقولتری از میانگین است. 10 معمولا چارک ها را در مواردی که تعداد داده ها کمتر از 25 است محاسبه نمی کنند. 11 میانگین نمونه پیراسته:تمامی مشاهدات کمتر از چارک اول و بیشتر از چارک سوم را برمی داریم و میانگین باقی مشاهدات را حساب می کنیم. 12 میانگین نمونه وینزوری:به جای مشاهدات کمتر از چارک اول مقدار چارکک اول و به جای مشاهدات بزرگ تر از چارک سوم مقدار چارک سوم را قرار داده ومیانگین داده های حاصل را محاسبه می کنیم. 13 مهم ترین معیار های پراکندگی عبارتند از:واریانس وانحراف معیار 14 میانگین انحرافها همیشه صفر است. 15 در مقایسه دو مجموعه از داده ها بیشتر بودن s در یک مجموعه حاکی از وجود پراکندگی بیشتر در آن مجموعه داده ها نسبت به مجموعه دیگر است. 16 هدف قاعده چبیشف بین این مطلب است که هر فاصله ای به مرکز و به طول Yks شامل نسبت کمینه ای از داده هاست 17 دامنه را اغلب در مواردی که تعداد نمونه کمتر از 8 است بکار می برند. 18 در توزیع هائی که دارای دنباله کشیده در یک جهت هستند دامنه میان چارکی نمونه به عنوان معیار پراکندگی بر واریانس ترجیح داده می شود. 19 اگر بافت نگار دارای نمودار متقارن باشد هر دو معیار گرایش به مرکز میانگین ومیانه یکی هستند. 20 فضای نمونه ای گسسته شامل اعداد تکی ولی فضای نمونه ای پیوسته شامل بازه ای پیوسته است. 21 در مواردی که عناصر فضای نمونه ای دارای احنپتمال هم شانس هستند ، دارای مدل احتمال یکنواخت هستند. 22 در اجتماع ...
آموزش احتمال

احتمال یکی از چندین کلمه ای است که برای بیان اتفاقات یا معلومات مشکوک به کار می رود. البته شانس، شرط بندی دیگر کلمات شبیه این، مفاهیمی مشابه احتمال را در ذهن ایجاد می کنند. در نظریه احتمال سعی بر ارائه مفهوم احتمال است.امروزه نظریه احتمال با بسیاری از شاخه های دیگر ریاضیات و بسیاری از حوزه های علوم طبیعی، تکنولوژی، و اقتصاد مرتبط است. ملاحظات تاریخی آغاز نظریه احتمال به اواسط قرن هفدهم باز می گردد. شرط بند با حرارتی با نام شوالیه دومره (de mere) حل مسئله ای را، که برایش مهم بود، از بلز پاسکال درخواست کرد. شرط بند با معلوم بودن این مطلب که در یکی از مراحل میانی بازی، یکی از آنها دور و دیگری دور راه برده باشد، و ، طبق قرار قبلی، اولین کسی که دور را ببرد برنده کل بازی باشد. پاسکال راه حل خود را با پی یردو فرما که او نیز راه حلی برای این مسئله به دست آورد. درمیان گذاشت و راه حل سوم از کریستین هویگنس (1629ـ 1695) به دست آمد. مردان فرهیخته مزبور، اهمیت مسنله مزبور را در بررسی قوانین حاکم بر پیشامدهای تصادفی دریافتند. به این ترتیب، مفاهیم و روش های اولیه علمی جدید، از مساله های مربوط به بازی های شانسی گسترش یافت. خیلی بعد، در قرن نوزدهم، توجه به سرعت افزاینده در علوم طبیعی، گسترش نظریه احتمال را به مواردی غیر از چهارچوب بازی های شانسی ضروری ساخت. گسترش مزبور رابطه ای تنگاتنگ با نام های ژاکوب برنولی (1654ـ1705)، آبراهام دوموآور (1667ـ1754)، پیرسیمون دولاپلاس (1749ـ 1827)، کارل فردریش گاوس (1777ـ 1855)، سیمون دنیس پواسون (1781ـ 1840)ف پافنونی لووبچ چبیشف (1821ـ1894)، آندری آندری ویچ مارکوف (1856ـ1922)، و در همین اواخر با اسامی الکساندر یاکوف لویچ خین چاین (1894ـ 1959) و اندری نیکولائویچ کولموگوروف (متولد 1903) داشته است. تحقیق در پیشامدهای انبوه با بررسی قوانین حاکن بر پیشامدهای تصادفی مرتبط است. به عنوان مثال، تولید کالایی که موارد کاربرد روزانه دارد پیشامد انبوه و ظهور کالایی معیوب در میان آنها پیشامدی تصادفی است. پیشامد پیشامد E ، به مفهوم پیشامد تصادفی ، نتیجه آزمونی است که گرچه میتواند رخ دهد ولی این رخ داد ضروری نیست . یک آزمون می تواند مشاهده یا آزمایش باشد و با مجموعه ای از شرایطی که باید برقرار شوند و با استفاده از تکرارپذیری مشخص می شود . حالت های حدی نیز به عنوان پیشامد در نظر گرفته می شوند : پیشامدحتمی ، پیشامدی است که به طور قطع رخ می دهد و پیشامد ناممکن، که هیچ گاه رخ نمی دهد از این قبیل اند. به عنوان مثال در انداختن یک تاس پیشامد آمدن عدد 7 یک پیشامد ناممکن پیشامد آمدن عدد 1 تا6 یک پیشامدحتمی است. پیشامدها را دو به هر ناسازگار می گوئیم اگر ...
بررسی نرمال‌بودن توزیع٬ آزمون کولوموگراف-اسمیرنوف

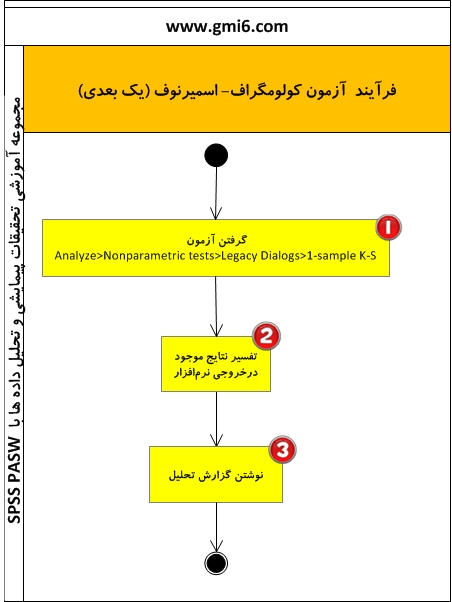
۱. هدف آزمون برای انتخاب آزمون درست برای تحلیل فرضیه‌ها٬ ابتدا باید از توزیع آماری متغیری که مورد آزمون قرار می‌گیرد٬ اطمینان حاصل کرد. برای نمونه٬ پیش‌نیاز گرفتن آزمون‌های پارامتری٬ نرمال‌بودن توزیع آماری متغیرهاست. به طور کلی می‌توان گفت که آزمون‌های پارامتری، عموما بر میانگین و انحراف معیار استوارند. حال اگر توزیع جامعه نرمال نباشد، نمی‌توان استنباط درست از نتایج داشت.برای بررسی توزیع آماری متغیرها از آزمون‌هایی استفاده می‌کنند. این آزمون‌ها به آزمون‌های نیکویی-برازش معروفند. آزمون کولوموگراف اسمیرنوف به همراه آزمون کای دو٬ جزو آزمون‌های نیکویی- برازش هستند. اما با توجه به محدودیت‌های آزمون کای‌دو٬ معمولا برای آزمون نرمال‌بودن٬ از آزمون کولوموگراف-اسمیرنوف استفاده می‌شود... . در این آزمون ‌، می‌توانید متغیر خود را بر مبنای این توزیع‌ها تست کنیدNormal نرمالPoisson پواسونUniform یکنواختExponential نمایی ۲.تحلیل نتایح با انجام این آزمون٬ نرم‌افزار یک عدد معنی‌داری محاسبه می‌کند. در آزمون نرمال‌بودن٬ چنان‌چه معنی‌داری (Sig) بيش‌تر از ۵ درصد یا ۵ صدم بود٬ نرمال‌بودن توزیع نتیجه گرفته می‌شود. باید به یاد داشت که آزمون کولموگراف-اسمیرنوف یک آزمون دو دنباله می‌باشد و برای تفسیر بهتر است این‌گونه بیان شود که عدد معنی‌داری بر ۲ تقسیم شده است و چنان‌چه این عدد بيش‌تر از ۲.۵ درصد یا ۲۵ هزارم باشد٬ توزیع نرمال است.
صد نکته از آمار و احتمال مقدماتی
صد نکته از آمار و احتمال مقدماتی 1 هدف اصلی آمار انجام استنباط درباره جامعه وسنجش میزان عدم حتمیتی که در این استنباط ها وجود دارد. 2 خلاصه کردن و توضیح خصوصیات مهم مجموعه داده ها را آمار توصیفی می نامند. 3 نمودارهای نقطه ای را وقتی بکار می برند که تعداد مشاهدات نسبتا کم باشد(کمتر از 20 یا 25)و بافت نگار برای مواردی است که تعداد مشاهدات زیاد است. ۴ در تشکیل جدول توزیع فراوانی انتخاب تعداد رده ها از طریق آزمایش و خطا انجام می شود و بسته به تعداد داده ها بین 5 تا 15 تغییر می کند. ۵ هیچگاه نباید برای نمایش داده های پیوسته از نمودار خطی استفاده کرد. 6 در نمایش بافت نگار اگر مستطیل ها در وسط دارای قله باشد آنگاه نمودار متقارن است ولی اگر مثلا سمت راست کشیده باشد چاوله به راست وبر عکس آن می شود چاوله به چپ. 7 هر معیار عددی که معرف مرکز مجموعه داده ها باشد معیار گرایش به مرکز است و از اصلی ترین آنها میانگین ومیانه است. 8 میانه نمونه ای:داده ها را بصورت مرتب و اگر تعداد داده ها(n) فرد باشد یک مقدار وسطی وجود دارد و در مورد nزوج که دو داده وسط وجود دارد متوسط آنها میانه است. 9 برای توزیع هائی که خیلی نامتقارن هستند میانه معیار معقولتری از میانگین است. 10 معمولا چارک ها را در مواردی که تعداد داده ها کمتر از 25 است محاسبه نمی کنند. 11 میانگین نمونه پیراسته:تمامی مشاهدات کمتر از چارک اول و بیشتر از چارک سوم را برمی داریم و میانگین باقی مشاهدات را حساب می کنیم. 12 میانگین نمونه وینزوری:به جای مشاهدات کمتر از چارک اول مقدار چارکک اول و به جای مشاهدات بزرگ تر از چارک سوم مقدار چارک سوم را قرار داده ومیانگین داده های حاصل را محاسبه می کنیم. 13 مهم ترین معیار های پراکندگی عبارتند از:واریانس وانحراف معیار 14 میانگین انحرافها همیشه صفر است. 15 در مقایسه دو مجموعه از داده ها بیشتر بودن s در یک مجموعه حاکی از وجود پراکندگی بیشتر در آن مجموعه داده ها نسبت به مجموعه دیگر است. 16 هدف قاعده چبیشف بین این مطلب است که هر فاصله ای به مرکز و به طول Yks شامل نسبت کمینه ای از داده هاست 17 دامنه را اغلب در مواردی که تعداد نمونه کمتر از 8 است بکار می برند. 18 در توزیع هائی که دارای دنباله کشیده در یک جهت هستند دامنه میان چارکی نمونه به عنوان معیار پراکندگی بر واریانس ترجیح داده می شود. 19 اگر بافت نگار دارای نمودار متقارن باشد هر دو معیار گرایش به مرکز میانگین ومیانه یکی هستند. 20 فضای نمونه ای گسسته شامل اعداد تکی ولی فضای نمونه ای پیوسته شامل بازه ای پیوسته است. 21 در مواردی که عناصر فضای نمونه ای دارای احنپتمال هم شانس هستند ، دارای مدل احتمال ...
توزیع گاما

توزیع گاما یکی از توزیع‌های احتمالی پیوسته است ‫و دارای دو پارامتر مقیاس θ، و پارامتر شکل k می‌باشد. اگر kعددی طبیعی باشد آنگاه توزیع گاما معادل است با مجموع k متغیر تصادفی با توزیع نمایی با پارمتر .تابع چگالی احتمال:‫که ‫در آن تابع گاما، θ پارامتر مقیاس، و k پارامتر شکل ‫می‌باشند.تابع گاما، انتگرالی همگراست و مقدار آن برابر با عددی مثبت است:ویژگی‌هاهرگاه k (پارامتر شکل) یک عدد صحیح و مثبت چون n باشد، می‌توان از توزیع گاما برای تخمین زدن مدت‌زمان لازم برای روی‌دادن n پیشامد استفاده نمود.توزیع مجموعاگر اگر n متغیر دو به دو مستقل از هم باشند، آنگاه:در نتیجه توزیع گاما بی‌نهایت تقسیم‌پذیر است.توزیع‌های مرتبطهرگاه k=۱ شود، حالت خاصی از توزیع گاما به وجود می‌آید که توزیع نمایی نامیده می‌شود.پارامترها ‫شکل (‫حقیقی)‫مقیاس (‫حقیقی) ‫تکیه‌گاهتابع چگالی احتمالتابع توزیع تجمعی‫ (سی‌دی‌اف)میانگینمیانه‫رابطه ساده صریح برای این پارامتر وجود نداردمُدواریانسچولگیکشیدگیانتروپی‫تابع مولد گشتاور (ام‌جی‌اف)تابع مشخصهتابع گاماتابع گاما تعمیم تابع فاکتوریل است از مجموعه اعداد طبیعی به مجموعه اعداد حقیقی و مختلط و برای یک عدد مختلط با بخش حقیقی مثبت به شکل زیر تعریف می‌شود:در ضمن برای هر عدد طبیعی z داریم:همچنین می‌توان ثابت کرد که:پارامتر مقیاساگر بتوان یک خانواده از توزیع‌های احتمالی را به کمک پارامتر s به شکل زیر نوشت: ‫آنگاه پارامتر s را پارامتر ‫مقیاس گویند.پارامتر شکلدر علم آمار و احتمالات پارامتر شکل به پارامتری گفته می‌شود که با تغییر آن، شکل تابع توزیع احتمالی تغییر می‌نماید (مقایسه نمایید با ‫‫پارامتر ‫مکان و ‫‫پارامتر ‫مقیاس) . بطور مثال توابع توزیع احتمالی زیر دارای پارامتر شکل می‌باشند:توزیع ارلانگتوزیع برتوزیع بتاتوزیع توانی نماییتوزیع گاماتوزیع مقدار نهایی تعمیم‌یافتهتوزیع پارتوتوزیع پیرسونتوزیع وایبولپارامتر مکاناگر بتوانیم یک خانواده از توزیع‌های احتمالی را به کمک پارامتر k به شکل زیر بنویسیم:‫آنگاه پارامتر k را پارامتر ‫مکان گوییم.
آموزش مطلب / متلب / Matlab

معرفی و دانلود رایگان کتاب و جزوه های مفید در برنامه نویسی متلب / مطلب (فارسی) همانطور كه مي دانيد برنامه نويسي مطلب يكي از ابزارهای مهم و كاربردي در شاخه هاي مختلف علوم است لذا با سرعت بالايی رو به گسترش و استفاده می باشد.در اين پست بنا به نيازي كه احساس مي كردم پيش روي دانشجويان و دانش پژوهان باشد، منابع ارزنده ای در مورد این برنامه قرار داده ام . زيرا منابع لاتين زياد و گيج كننده و منابع فارسي اندك و پراكنده بودند. اين نياز مخصوصاَ براي دانشجويان مشغول به تحصيل در خارج از ايران بيشتر احساس مي شد. چون منابع فارسي مطلب دور از دسترس و منابع و كتب لاتين صد البته بسیار گران قیمت. در پايان اشكالات را به بزرگي خود ببخشيد و در صورتيكه منبع يا منابع مفيد ديگري مي شناسيد معرفي نماييد تا ساير دوستان هم بهرهمند گردند. لیست مندرجات خودآموزهای فارسی مطلب ۱-كتاب آموزش مطلب به كوشش مشكي باف و برمكي : الگوریتم و الگوریتم نویسی در مطلب / نصب مطلب / تعریف متغییر و ماتریس / اندیس ماتریس / عملگرها و توابع / پارامترهای اولیه / دستورهای ابتدایی / input دریافت مقداری برای متغییر / disp نمایش آرایه یا متغییر / clc پاک کردن صفحه نمایش / home بردن مکان نما به صفحه اول / clear پاک کردن متغییر / nargin تعداد ورودی های تابع / nargout تعداد خروجی های تابع / beep تولید صدای بیپ / m-file / Matlab Function / کنترل در برنامه نویسی / توابع شرطی if while switch / توابع چرخه ایelse for while/ چند شرط همزمان / elseif / swith case end / continue/ break / منطق در شرط / گرد کردن / گرد کردن / توابع عددی / prims عدد اول / factor تجزیه به عدد اول / factorial فاکتوریل / کوچکترین مضرب مشترک gcd / lcm بزرگترین مقسوم علیه مشترک / توابع مختلط / abs قدر مطلق / complex / imag قسمت موهومی عدد مختلط imag / / قسمت حقیقی عدد مختلط Real / Angle / مزدوج مختلط Conj مقدار زاویه قطبی مختلط/ ساخت عدد مختلط / توابع نمایی / Sqrt ریشه دوم / sqrtm ریشه دوم ماتریس / توان nthroot / power توان / pow2 توان در مبنای دو / exp تابع نمایی / لگاریتم log ریشه nام عدد / توابع مثلثاتی / دستورات منطقی در برنامه نویسی / Isempty / Isnumeric عدد است یا نه / Isequal برابر است یا نه / Isreal حقیقی است یا نه / خالی است یا نه isprime عدد اول بودن / توابع زمان Clock / Date / Tic ... toc / pause / توابع آرایه ای / numel / طول بردار lenghth /پیدا کردن درایه خاص / اندازه گیری مرتبه ماتریس find / size تعداد اعضای آرایه /ماتریسهای خاص magic ماتریس جادویی / rand ماتریس تصادفی / eye /ماتریس یک ones / zeroes ماتریس صفر ماتریس همانی / توابع ماتریسی / max بزرگترین درایه در ماتریس / min کوچکترین درایه در ماتریس / sort مرتب کردن ...