دانشگاه پیام نوربستان اباد
تابع لژاندر (Legander Function)
یکی از تابع های مهم دیگر تابع لژاندر می باشد که خاصیت مهمی را ارائه می کند برای دیدن کافی است دانلود کنید:دانلود کنید
سخنان حکمت
آنتونی رابینز از کتاب اسرار موفقیت به نوشته ی پاتریک چان به مترجمی فرهاد فروغمند 1- راه دستیابی به موفقیت عمل گسترده و مصمم است. 2- عمل کلید بنیادی رسیندن به موفقیتهاست. 3- اگر همان کاری راکنید که همیشه می کردید به همان چیزی می رسید که تاکنون رسیده اید. 4- در لحظات تصمیم گیری است که سرنوشت شما شکل می گیرد.
تقدیر از استاد نمونه آقای دکتر کمال بهمن پور
فرصتی یافتم تا از استادم جناب آقای دکتر کمال بهمن پور که محرک وانگیزه من در تحصیل رشته ریاضی و پا گذاشتن در زیباییهای نهفته در ریاضی که کسی که عاشق نشود نمی تواند آن را به درستی بشناسد و درک کند بودند، را تقدیر کنم وبتوانم گوشه ای از زحماتی را که برای یادگیری صحیح وروشن علم به دانشجویان مثل من که بدون هیچ خستگی کشیدند باشد.ایشان دکتر کمال بهمن پورمتولد 1356می باشند که کارشناس ریاضی محض از دانشگاه بوعلی سینای همدان اخذ کردند وکارشناسی ارشد را بدون وقفه ای در سال 1380از دانشگاه تهران در گرایش ریاضی محض گرایش جبر اخذ نمودند ودکتری ریاضی را در گرایش جبر جابه جائی در سال 1388 از دانشگاه تبریز اخذ نمودند.استادان راهنمای ایشان آقایان دکتر رضا نقی پور و دکتر علی اکبر مهرورز که جزء استادان طراز اول دانشگاه تبریز می باشند . عنوان رساله ایشان:"Cofiniteness and associated primes of local cohomology modules" خلاصه رساله ایشان به شرح زیر می باشد: قبلا توسط محققین مختلفی نشان داده شده بود که روی حلقه موضعی نوتری ، مدول های کوهمولوژی موضعی یک مدول یا یا تولید متناهی نسبت به یک ایده آل هم متناهی است. ایشلن در رساله خود نشان داده اند که می توان فرض موضعی بودن حلقه را حذف کرد که این نیز موجب متناهی شدن مجموعه ایده آل های اول وابسته مدول های کوهمولوژی موضعی تحت شرایط خاص می شود.همین طور به مباحثی از قبیل خواصی از رتبه حسابی ایده آل های ونامتناهی بودن ایده آل های اول وابسته دوگان مانتیس مدول های کوهمولوژی موضعی پرداخته است. مقالات استخراج از رساله ایشان به شرح زیر می باشد: K.Bahmanpour and R.Naghipour, Associated primes of local cohomology modules and matlis duality, journal of Algebra,320(2008),2632-2641.K.Bahmanpour and R.Naghipour, Cofiniteness of local cohomology modul for ideals of small dimension, Journal of Algebra, 321(2009), 1997-2011. K.Bahmanpour and R.Naghipour, On the cofiniteness of local cohomology modules, Proc, Amer.Math.Soc.,136(2008), 2359-2363.K.Bahmanpour and R.Naghipour and M.Sedghi, cofiniteness of local cohomology modules and Hunekes conjecture, Rocky Mountain Journal of mathematics.(in press).A.A. Mehrvarz, K.Bahmanpour and R.Naghipour, Arithmetic rank , cohomo-logical dimension and filter regular sequences , J. Algebra and its applications , 8(2009) , 855-862.به درستی گفته اند: از پدر گر قالب تن یافتیم از معلم جان روشنیافتیم. امیدوارم هرکجای ایران زمین به امر معلمی مشغولند درسلامت کامل بوده و با موفقیت همراه باشند.
آموزش انتگرال
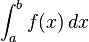
نتگرالها يک بحث اساسي رياضيات عالي را تشکيل داده که ميتوان کاربرد آنرا درتمام علوم طبيعي، انساني وغيره مورد مطالعه قرارداد.اولين بار لايب نيتس نماد استانداردي براي انتگرال معرفي کرد. aو b نقاط ابتدا و انتهاي بازه هستند و f تابعي انتگرالپذير است و dx نمادي براي متغير انتگرال گيري است. از لحاظ تاريخي dx يک کميت بي نهايت کوچک را نشان ميدهد. هر چند در تئوريهاي جديد، انتگرال گيري بر پايه متفاوتي پايه گذاري شده است. تابع اوليه هر گاه معادله مشتق تابعي معلوم باشد وبخواهيم معادله اصلي تابع را تعيين کنيم اين عمل را تابع اوليه مي ناميم. تعريف: تابع اوليه y = f(x)را تابعي مانند Y = F(x) + c مي ناميم،هرگاه داشته باشيم: cعدد ثابت (y = F(x) + c)' = y = f(x) انتگرال نامعين تعريف:هرگاه معادله ديفرانسيلي تابعي معلوم باشد وبخواهيم معادله اصلي تابع را معلوم کنيم اين عمل راانتگرال نا معيين ناميده و آن را با نماد نمايش مي دهند. بنا به تعريف نماد را انتگرال نامعين ناميده وحاصل آن را تابعي مانندF(x) + c در نظر ميگيريم هر گاه داشته باشيم: با شرط: (F(x) + c)' = f(x) انتگرال معين بنا به تعريف نماد را انتگرال معين ناميده و حاصل آن را عددي به صورت زير تعريف ميکنيم: a aوb را به ترتيب کرانهاي بالا و پايين انتگرال ميناميم. تابع انتگرالپذير اگر تابعي داراي انتگرال باشد به آن انتگرالپذير گويند. تعبير هندسي انتگرال از نظر هندسي انتگرال برابر است با مساحت سطح محصور زير نمودار. نکته! انتگرال نمودار سه بعدي(انتگرال سه گانه)معرف حجم محصور زير نمودار است. انتگرال يک تابع مثبت پيوسته در بازه (0,10) در واقع پيدا کردن مساحت محصور بين خطوط x=0 , x=10 و خم منحني fx است. aو b نقاط ابتدا و انتهاي بازه هستند و f تابعي انتگرالپذير است و dx نمادي براي متغير انتگرال گيري است. انتگرال يک تابع مساحت زير نمودار آن تابع است. انتگرال گيري انتگرال گيري به معني محاسبه سطح زير نمودار با استفاده از روشها وقوانين انتگرال گيري است. 1.f تابعي در بازه (a,b) در نظر ميگيريم. 2.پاد مشتق f را پيدا ميکنيم که تابعي است مانند f که و داريم: 3.قضيه اساسي حساب ديفرانسيل و انتگرال را در نظر ميگيريم: بنابراين مقدار انتگرال ما برابر خواهد بود. به اين نکته توجه کنيد که انتگرال واقعاً پاد مشتق نيست (يک عدد است) اما قضيه اساسي به ما اجازه ميدهد تا از پاد مشتق براي محاسبه مقدار انتگرال استفاده کنيم. معمولاً پيدا کردن پاد مشتق تابع f کار سادهاي نيست و نياز به استفاده از تکنيکهاي انتگرالگيري دارد اين تکنيکها عبارتاند از : انتگرال گيري بهوسيله تغيير متغير انتگرال گيري جزء به جزء : انتگرال ...
سخنانی از پروفسور محمود حسابی
1- سه اصل عاشقی : محبت ، احترام و راستگویی است. 2- هنر ، چاشنی زندگی است. 3- داشتن هدف ورفتن به دنبالش خوب است ولی عاشق هدف بودن وگرفتار شدن چیز دیگری است. 4- عشق به وجود آورنده اعمال زیباست. 5- فعال باشیم اما ملایم عادل باشیم ولی با گذشت.
