حل دستگاه معادلات در متلب
حل معادلات دیفرانسیل با متلب
متلب امکانات زیادی را برای حل معادلات دیفرانسیل و دستگاه های معادلات دیفرانسیل در اختیار شما می گذارد. در این جا یک دستور پرکاربرد را معرفی میکنم که برای حل معادلات دیفرانسیل معمولی (ode) به كار مي رود. دستور dsolve به راحتي معادلات ديفرانسيل با هر مرتبه اي را براي شما حل مي كند. ابتدا خوب است مثالي از حل يك معادله ديفرانسيل ساده را با آن ببينيد: >> dsolve('Dy+2*x=0','x') با اجراي دستور بالا متلب پاسخ زير را مي دهد:ans = C1 - x^2 براي دادن معادله به تابع dsolve بايد نكات زير را در نظر داشته باشيد: ١. كل معادله بايد داخل علامت هاي ' ' قرار بگيرد. براي بقيه پارامترهاي دستور هم بايد اين قانون رعايت شود. 2. پارامتر دوم دستور متغير مستقل معادله را مشخص مي كند (كه در مثال بالا x است). جواب متلب همان متغير وابسته (تابع مجهول) است (در مثال بالا پاسخ برابر y است). ضمنا اگر متغير مستقلي مشخص نكنيد متلب حرف t را به عنوان متغير مستقل فرض خواهد كرد. 3. مشتق يك تابع را بايد با حرف D (بزرگ) نشان دهيد به طوري كه نام تابع بلافاصله بعد از آن بيايد (مثل Dy كه به معني مشتق y نسبت به x است). مشتق هاي مرتبه دوم به بعد را به صورت D3y,D2y و... وارد كنيد. مثل بقيه قسمت هاي متلب علامت ضرب بايد حتما با * مشخص و توان با ^ مشخص شود و پرانتزها و ديگر علائم هم رعايت شوند. ٤. C در پاسخ داده شده يك ثابت است كه معمولا يك شماره هم همراه آن است تا از ثابت هاي قبلي متمايز شود. 5. اگر معادله داراي شرايط اوليه است آن را هم ميتوانيد به متلب بدهيد. به اين شكل كه شرط اوليه به عنوان پارامتر دوم (و اگر چند شرط باشد به عنوان پارامترهاي بعد) به دستور داده ميشود. مثلا ' 2 = (0)y ' را به عنوان شرط اوليه مي توان به نرم افزار داد. در ادامه چند مثال ديگر از دستور dsolve را ملاحظه ميكنيد: >>dsolve('Dy+2*t=t^2','y(0)=2','t') >> dsolve('D2y+5*Dy+3*y=10','Dy(0)=20','y(0)=0') >>dsolve('Dy+10*y=5*x','x') دستور dsolve معادلات را به شيوه سيمبوليك (جبري) حل مي كند. متلب دستورات قوي اي هم براي حل معادلات ديفرانسيل به شيوه محاسبات عددي دارد. مقاله زير حل انواع معادلالت ديفرانسيل با متلب را به طور كامل آموزش مي دهد: http://www.cs.rice.edu/~nakhleh/COMP572/Papers/matode.pdf
حل دستگاههای خطی N معادله با N مجهول در MATLAB
در موارد بسیاری نیاز است تا تعداد معینی معادله خطی با همان تعداد معین از مجهولات را حل کنیم. برای نمونه در زمینههایی مانند تحلیل مدارات الکترونیکی، مدلسازی آب و هوا، CT Scan (computed axial tomography) و موارد بسیار دیگر، با این مبحث ریاضی روبرو خواهیم بود. یک شکل نمونه از یک دستگاه با چهار معادله و چهار مجهول به فرم زیرمفروض است: 2a + 2b + 1c + 6d = 4 4a – 2b + 0.5c +1d = 2 6a + 1b + 0c – 1d = -1 2a + 2b – 1c + 3d = 4 در اینجا ما باید مقادیر a, b, c, d را طوری بیابیم که همه معدلات ارضاء گردند. برای حل دستگاههای معادلات خطی در مقاطع راهنمایی و دبیرستان مطالب زیادی آموختهایم. و روشهای متعددی نیز برای این امر وجود دارد. که از آن جمله می توان به روش حذفی و روش کرامر اشاره کرد. اما در محیط MATLAB دستوراتی برای حل این معادلات وجود دارد که از روش ضرب ماتریس (اسکالر) استفاده می کند. برای همین دو عدد ماتریس از طرفین معادله به فرم زیر تشکیل داده می شود: A=[2 3 1 6 4 -2 .5 1 6 1 0 -1 2 2 -1 3] B=[4 2 -1 4] حال بایستی ماتریس A معکوس گردد و سپس در ماتریس B ضرب گردد. و حاصل در یک ماتریس دیگر ذخیره گردد؛ دستورات MATLAB به فرم زیر خواهد بود: x=inv(A)*B و یا x=A^(-1)*B و نیز می توان از دستور x=A\Bاستفاده کرد که این دستور بسیار بهینه و قابل اعتماد نسبت به دو مورد قبلی است. ماتریس x که از حاصلضرب دو ماتریس اول بدست آمده یک ماتریس یک ستونه و چهار سطری می باشد که مجهولات معادلات به فرم زیر در آن جای گرفته اند: a=x(1) b=x(2) c=x(3) d=x(4) این روش در عین سادگی فوق العاده گاهی وقتها نیز دچار مشکل می شود و جوابهای صحیح را بدست نمی دهد و یا گاها چند جواب متفاوت را در متغییرهای متعدد می دهد، (مخصوصاً در زمان استفاده از دستور inv(A)) برای اجتناب و پیشگیری از این مشکل، در دستگاه معادلات، بایستی به N مجهول دقیقاً N معادله خطی مستقل داشته باشیم. و معادله مستقل معادله ای است که با افزودن یک مقدار به معدله دیگر بدست نیاید. یعنی کاملا با معدلات دیگر متفاوت باشد!. البته همیشه نمی توان با یک نگاه ساده به معادلات به مستقل بودن آنها پی برد! بنابراین در MATLAB برای حل این مشکل از دستور Rank() استفاده می کنیم که در صورت دادن ماتریس مرجع به آن، تعداد معادلات مستقل را مشخص خواهد نمود. یک مثال کاربردی در تصویربرداری پژشکی: http://homepages.udayton.edu/~hardierc/ECE203/lineareq.htmhttp://en.wikipedia.org/wiki/System_of_linear_equations
حل معادلات دیفرانسیل معمولی با استفاده از نرم افزار متلب
حل معادلات دیفرانسیل معمولی با استفاده از نرم افزار متلب جدیدترین کار همشهریمان مهندس هادی بهمنی کارشناسی ارشد خطوط راه آهن دانشگاه علم و صنعت تهران شرح : در این کتابچه 30 صفحهای سعی شده است که با زبانی روان و با استفاده از ابتدایی ترین و در عین حال اساسی ترین توابع داخلی نرم افزار متلب ، شیوه حل انواع معادلات و دستگاه های دیفرانسیل معمولی شرح داده شود . انواع معادلات دیفرانسیل معمولی بحث شده شامل مسائل مقدار مرزی و مقدار اولیه می باشند . در بخش پنجم این کتابچه همچنین شیوه کد نویسی برای حل عددی معادلات دیفرانسیل به روش اویلر و تیلور به طور اجمالی بحث شده است . مطالعه این کتابچه برای دانشجویانی که قصد دارند به طور اصولی و علمی با شیوه حل معادلات دیفرانسیل در نرم افزار متلب آشنا شوند ، ضروری است . مهمترین منبع این کتابچه کتابی است تحت عنوان : حل معادلات دیفرانسیل معمولی با نرم افزار متلب که منتشره از انتشارات دانشگاه کمبریج می باشد. بسیاری از کدهای به کار رفته در این کتاب دوباره به زبانی ساده بازنویسی شده اند تا برای کاربران مقدماتی نرم افزار قابل فهم تر باشند . دریافت فایل
حل معادلات خطی در متلب
سیاری از معادلات خطی قابل نمایش به فرم ماتریسهای ساده می باشند و می توان با قوانین مربوط به ماتریسها به راحتی اقدام به حل اینگونه معادلات نمود . برای مثال دستگاه زیر را در نظر بگیرید :
پروژه برای درس محاسبات عددی
معادلات يك متغيرهدرونيابي و تقريب چند جملهاي انتگرالگيري و مشتقگيري عددي حداقل مربعات و نظريه تقريب حل دستگاه به روش مستقيم حل دستگاه به روش تكراري حل دستگاه غير خطي مسائل مقدار اوليه مسائل مقدار مرزي المان محدود تفاضل محدود مقادير ويژه معادلات ديفرانسيل معمولي معادلات ديفرانسيل جزئيمعادلات يك متغيرهروش نصف كردن BISECTION METHOD روش سكانت SECANT METHOD روش موقعيت مصنوعي(غلط) METHOD OF FALSE POSITION روش نيوتن - رافسون NEWTON-RAPHSON METHOD روش مولر MULLER'S METHODدرونيابي و تقريب چند جملهايروش درونيابي لاگرانژ(نويل) LAGRANGE'S INTERATED INTERPOLATION روش درونيابي تفاضلات تقسيمشده نيوتن NEWTON'S INTERPOLATORY DIVIDED-DIFFERENCE FORMULA روش درونيابي هرميت HERMITE INTERPOLATION روش اسپلاين مكعب طبيعي NATURAL CUBIC SPLINE روش اسپلاين مكعب مقيد CLAMPED CUBIC SPLINE روش منحني بريز BEZIER CURVE METHOD نتگرالگيري و مشتقگيري عدديروش انتگرال مركب سيمپسون COMPOSITE SIMPSON'S METHOD روش انتگرال رامبرگ ROMBERG METHOD روش انتگرال قابل تطبيق كودريچر ADAPTIVE QUADRATURE روش انتگرال دوگانه سيمپسون COMPOSITE SIMPSON'S METHOD FOR DOUBLE INTEGRALS روش انتگرال دوگانه گوس GAUSSIAN QUADRATURE FOR DOUBLE INTEGRALS روش انتگرال سهگانه گوس كودريچر GAUSSIAN QUADRATURE FOR TRIPLE INTEGRALS روش انتگرال سهگانه سيمپسون COMPOSITE SIMPSON'S METHOD FOR TRIPLE INTEGRALS حل عددي مسائل مقدار اوليهروش اويلر EULER'S METHOD روش رانگ - كوتا مرتبه چهار RUNGE-KUTTA (ORDER 4) METHOD روش پيشگو - اصلاحگر مرتبه چهار آدامز ADAMS-FOURTH ORDER PREDICTOR-CORRECTOR METHOD روش برونيابي EXTRAPOLATION METHOD روش رانگ - كوتا - فلبرگ RUNGE-KUTTA-FEHLBERG METHOD روش پيشگو - اصلاحگر با اندازه گام متغير آدامز ADAMS VARIABLE STEP-SIZE PREDICTOR-CORRECTOR METHOD روش رانگ - كوتا براي سيستم معادلات ديفرانسيل RUNGE-KUTTA METHOD FOR SYSTEMS OF DIFFERENTIAL EQUATIONS روش ذوزنقهاي با تكرار نيوتن TRAPEZOIDAL METHOD WITH NEWTON ITERATIONروشهاي مستقيم حل دستگاههاي خطيروش حذفي گوس با جايگذاري پسرو GAUSSIAN ELIMINATION WITH BACKWARD SUBSTITUTION METHOD روش حذفي گوس با محورگيري ستوني ماكزيمال GAUSSIAN ELIMINATION WITH MAXIMAL COLUMN PIVOTING روش حذفي گوس با محورگيري ستوني مقياس شده GAUSS-JORDAN روش تجزيه مستقيم DIRECT FACTORIZATION روش چولسكي CHOLESKI'S METHOD روش فاكتورگيري LDL-T FACTORIZATION روش تحويلگيري كروت براي دستگاههاي خطي سه قطري CROUT REDUCTION FOR TRIDIAGONAL LINEAR SYSTEMSروشهاي تكراري حل دستگاههاي خطيروش تكرار ژاكوبي JACOBI ITERATIVE METHOD روش تكرار گوس - سيدل GAUSS-SEIDEL ITERATIVE METHOD روش فوق تخفيف متوالي (SOR) SOR METHODنظريه تقريبسهم تقريبي Pade PADE RATIONAL APPROXIMATION METHOD سهم تقريبي چبيشف CHEBYSHEV RATIONAL APPROXIMATION تبديل فوريه سريع FAST FOURIER TRANSFORMتقريب مقادير ويژهروش تواني POWER METHOD روش تواني براي ماتريسهاي متقارن SYMMETRIC POWER METHOD روش تواني معكوس INVERSE POWER METHOD روش تقليل ويلاند WIELANDT'S DEFLATION روش هاوس ...
حل عددی معادلات غیر خطی _ روش تیلور
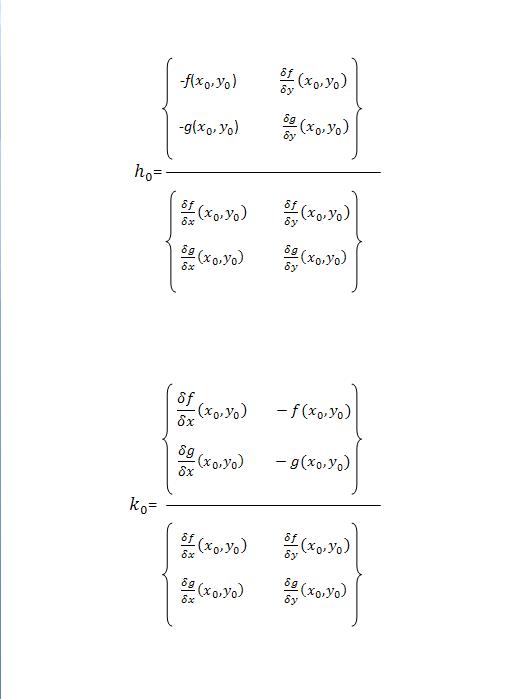
به عنوان مثال می خواهیم با استفاده از روش تیلور دستگاه معادلات غیر خطی زیر را حل کنیم:f(x,y)=x^2+y-11g(x,y)=x+y^2-7x0=3.5y0=1.5الگوریتم روش تیلور به صورت:x1=x0+h0y1=y0+k0حل به کمک برنامه :(x,y]=taylor_method(f,g,x0,y0,i]که i معرف تعداد تکرار میباشدsyms x y<<f=x^2+y-11<< g=x+y^2-7<< (x,y]=taylor_method(f,g,3.5,1.5,2]<<=x1 2.967249950288328 =y1 2.000514515808312 برای دریافت فایل کلیک کنیدMohandesaan.Blogfa.com
دانلود رایگان حل دستگاه معادلات دیفرانسیل معمولی با استفاده از نرم افزار متلب(مهندس حسن فراهانی)
دانلود رایگان حل دستگاه معادلات دیفرانسیل معمولی با استفاده از نرم افزار متلب تهیه کننده : مهندس هادی بهمنی – کارشناس ارشد عمرانزمستان 1393 نقل قول :توضیح : در بسیاری از موارد در تحلیل دینامیکی سیستم ها یا موارد دیگر، به دستگاه معادلات دیفرانسیل با شرایط اولیه میرسیم که برای تعیین پاسخ سیستم به روش حل مستقیم دستگاه معادلات دیفرانسیل حاکم، باید این دستگاه را به طرق مختلف حل کنیم. یکی از روشهای کارآمد جهت حل، روش رانگ کوتا از مرتبه های مختلف آن میباشد. در این نوشتار هدف، شرح روش رانگ کوتا نمیباشد، بلکه میخواهیم نحوه استفاده از یکی از توابع داخلی کارآمد متلب را برای حل دستگاه معادلات دیفرانسیل معمولی با مقدار اولیه به روش رانگ کوتا شرح دهیم. دستور ode45 در متلب بر اساس فرمول رانگ کوتای مرتبه چهار یا پنج صریح عمل میکند. دستور ode45 یک حل گر تک گامی میباشد بدین معنی که برای پیدا کردن مقدار y(tn) فقط کافیست مقدار y(tn-1) معلوم باشد... برای دانلوداینجا کلیک کنید...http://s5.picofile.com/file/8169758284/ode45_fun.pdf.htmlبازگشت به صفحه اصلی وبلاگ مهندسی عمران راه و ساختمان(مهندس حسن فراهانی) منبع
لیست پروژه های انجام شده با متلب matlab و فرترن
ریشه یابی به کمک روش نیوتن رافسون newton-raphson ریشه یابی با روش میانیابی خطی با متلب ریشه یابی با روش نصف کردن یا تنصیف ریشه یابی با روش نقطه ثابت با g(x) یا set point ریشه یابی با روش مولر حل دستگاه چند معادله چند مجهول با روش حذفی گوس(گاوس) حل دستگاه چند معادله چند مجهول با روش تجزیه ماتریس LU حل دستگاه چند معادله چند مجهول با روش ژاکوبی(جاکوبی) حل دستگاه چند معادله چند مجهول با روش گوس سایدل حل دستگاه چند معادله چند مجهول با روش توماس حل معادله دیفرانسیل به روش اولر-اولر اصلاح شده حل معادله دیفرانسیل به روش رونگ کوتای مرتبه 2 و رونگ کوتای مرتبه 4- Runge kutta (RK4) حل معادله دیفرانسیل به روش آدامس میلتون حل معادله دیفرانسیل به روش شوتینگ shooting method حل معادله دیفرانسیل به روش صریح explicit حل معادله دیفرانسیل به روش ضمنی implicit حل مساله انتقال حرارت پایا تشخیص علائم رانندگی با متلب الگوریتم آموزشی levenberg marquardt backpropagation تشخیص هوشمند بیماریهای قلبی با شبکه عصبی و ژنتیک استفاده از خوشه بندی در تشخیص سرطان سینه به کمک هوش مصنوعی خوشه بندی برای تشخیص نوع گیاه زنبق و سوسن خوشه بندی نوع اختلالات کبد روی دادههای آزمایش خون و میزان مصرف مشروبات الکلی با انفیسANFIS تشخیص دیابت زنان با به کار گیری روش فازی عصبی پیدا کردن خطای شبکه ماهواره با شبکه عصبی mlp تشخیص حروف و اعداد با پردازش تصویر حل عددی معادلات دیفرانسیل با متلب برازش منحنی مساله بهینه سازی چند هدفه رسم مخروط و کره و چند ضلعی ها کوتاه سازی با نرم افزار متلب پروژه های حوزه سلامت با matlab حل مسایل تیر و خرپای سه بعدی FEM حل مسایل مشتق (central,forward,backward) حل چند معادله چند مجهول غیر خطی کلاس بندی داده ها کلونی مورچه ها با مطلب(متلب) پروزه کنترل و کنترل مدرن شبیه سازی مقالات کنترل، دینامیک و ارتعاشات حل به کمک روش کرانک نیکولسون حل مسایل دیتا ماینینگ data mining حل معادلات دیفرانسیل با شبکه عصبی پروژه های کنترل دیجیتال حل مسایل مختلف دینامیکی مسایل تحقیق در عملیات پروژه المان محدود با متلب انحراف معیار و واریانس کلیه پروژه های آماری اعتبار سنجی اکولایزر سیگنال صوتی یافتن مقدار مینیمم و ماکسیمم (کمینه و بیشینه توابع با قیود) شبیه سازی، پیکربندی و تنظیم صورت (face aligment) پیاده سازی پروژه تلفات فیبرنوری حل معادلات دیفرانسیل پاره ای با شرایط مرزی مختلف حل معادله بسل انتقال حرارت در فین و صفحه مستطیلی یافتن اشیا به کمک پردازش تصویر image processing حل مساله انتقال حرارت دو بعدی و معادلات لاپلاس، بیضوی و سهموی حل دستگاه با فرترن روش سکانت به دست آوردن ضرایب لاگرانژ ...
