جدول مشتق توابع
نکاتی پیرامون ریاضی عمومی
صفحه اصلی وبلاگ۱. اثبات اصم بودن عدد پی: توضیحات: در این نکته، برهان مشهور "ایوان نیو ِن" را در اثبات اصم بودن عدد پی مشاهده می فرمایید. ( مقاله اصلی را می توانید با مراجعه به اینجا دانلود کنید. چند اثبات دیگر را در سه منبع ۱ ،۲ و ۳ مطالعه فرمایید. با تایپ عبارت "PI is Irrational" در گوگل به مطالب دیگری نیز دست خواهید یافت.) ۲. اثبات اصم بودن عدد e : توضیحات: می دانیم که عدد مشهور e عددی اصم است. در این نکته برهان کوتاهی از این مطلب را خواهید دید. ۳. بررسی ریشه های مشتق یک تابع به وسیله قضیه آخر فرما: توضیحات: در این نکته مولف تابعی خاص را در نظر گرفته و به وسیله آخرین قضیه فرما یا FLT ، ثابت می کند که مشتق این تابع در x=0 ، صفر نمی شود. (برای اطلاعات کلی پیرامون آخرین قضیه فرما به اینجا و اینجا مراجعه فرمایید. با تایپ عبارت "Fermat's Last Theorem" در گوگل به مطالب دیگری نیز دست خواهید یافت.) ۴. فرمولهایی برای محاسبه عدد پی: توضیحات: در این نکته، سریهای همگرایی را که به وسیله آنها عدد پی محاسبه می شود، ملاحظه خواهید کرد. البته در این مقاله، فرمولهای دیگری نیز در همین رابطه وجود دارد.۵. مجموع توانهای k ام اعداد طبیعی 1، 2،...،n : توضیحات: در این نکته، فرمولهای جالبی برای به دست می آید. ۶. دوازده مقاله کوتاه و جالب پیرامون عدد پی توضیحات: با کلیک بر پیوند بالا وارد صفحه ای خواهید شد که شامل ۱۲ مقاله با قالب pdf پیرامون «عدد پی» است. مطالعه بعضی از این مقالات به معلوماتی از آنالیز ریاضی نیازمند است. موضوعات این مقاله ها عبارتند از: - محاسبه عدد پی به روش ارشمیدس - ارتباط بیضی، منحنی حلزونی ارشمیدس و سیکلوئید با عدد پی - منحنی هایی با طول ثابت - فرمولهای «ویت Viete» و «والیس Wallis» - چند سری نامتناهی برای عدد پی - استفاده از تابع آرکتانژانت برای محاسبه عدد پی - فرمولی شگفت انگیز از اویلر - پی و سری فوریه - عدد پی و عدد e - اصم بودن عدد پی - فرمولهای گاوس، رامانوجان و بیلی-بوروین-پلوف برای محاسبه سریعتر عدد پی - پی در نظریه احتمال ...
فرمولهای مشتق و انتگرال
مشتق توابع (قالب pdf) توضیحات: در این جدول، قوانین کلی مشتق گیری و نیز فرمولهای مشتق توابع نمایی و لگاریتمی،توابع مثلثاتی و معکوس مثلثاتی و مشتق توابع هذلولوی و معکوس هذلولوی را مشاهده خواهید کرد. این جدول شامل ۳۶ فرمول مختلف است. جدول بزرگ انتگرالهای توابع (فالب pdf) توضیحات: این جدول شامل ۱۲۰ انتگرال مختلف در ۱۰ فرم متفاوت از توابع است. حل معادلات درجه اول تا چهارم توضیحات: با کلیک بر عبارت بالا وارد سایتی خواهید شد که در آن مقالات کوتاه متعددی درباره حلمعادلات درجه اول تا چهارم و معادلات خطی دیگر گنجانده شده است. منبع : دانلود کتاب مهندسی الکترونیک مهندسی عمران
تابع لگاریتمی
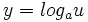
توابع لگاریتم در پایه محاسبه ی قواعد حاکم بر توابع لگاریتمیمشتق آهنگ های نسبی رشد توابع لگاریتم در پایه همچنین ببینید: توابع لگاریتم در پایه می دانیم که اگر عدد مثبتی به جز یک باشد، تابع مشتق پذیر و یک به یک است. علاوه بر این، مشتق آن یعنی ، هرگز صفر نمی شود. پس این تابع یک معکوس مشتق پذیر دارد که آن را " لگاریتم در پایه ی " نامیده و با نشان می دهند. چون و معکوس یکدیگرند، ترکیب آن ها به هر ترتیبی، تابع همانی است. پس روابط زیر به دست می آیند: بنابر این لگاریتم در پایه ی ، نمایی است که باید به توان آن برسد تا به دست آید. محاسبه ی عدد را همیشه میتوان به کمک فرمول زیر از لگاریتم های طبیعی و به دست آورد: این فرمول را می توان با روش زیر استنتاج کرد: قواعد حاکم بر توابع لگاریتمی الف)ب)ج) مشتق اگر تابع مشتق پذیری از باشد، آنگاه: چرا که: آهنگ های نسبی رشد توابع ممکن است توجه کرده باشید که توابع نمایی نظیر و ، وقتی بزرگ می شود، خیلی سریع تر از چند جمله ای ها و توابع گویا رشد می کنند. به ویژه این توابع نمایی خیلی سریع تر از تابع صعود خواهند کرد و وقتی زیاد می شود، بیش از فزونی می گیرد. در واقع وقتی ، توابع و تندتر از هر توان مثبتی از ، رشد می کنند. در مقابل، توابع لگاریتمی نظیر و ، که معکوس توابع و می باشند، وقتی ، از هر توان مثبتی از رشد کمتری دارند. به عنوان مثال اگر محور ها را با سانتیمتر مدرج کنیم، باید روی محور به اندازه ی چهار سال نوری جلو برویم تا نقطه ای بیابیم که به ازای آن ارتفاع نمودار تنها بشود. توجه: هر دو تابع لگاریتمی و ، وقتی ، با یک آهنگ رشد می کنند چرا که: و این حد همیشه متناهی و مخالف صفر است. لگاریتم در پایه لگاریتم های در پایه ، که غالبا " لگاریتم های معمولی " نامیده می شوند، در بسیاری از فرمول های علمی ظاهر می گردند. مثلا"، شدت زمین لرزه که بر حسب ریشتر گزارش می شود، دارای فرمولی به شرح زیر است: که در آن دامنه حرکت زمین بر حسب میکرون در ایستگاه گیرنده، دوره تناوب موج زلزله بر حسب ثانیه و ثابتی تجربی است که میزان تضعیف موج زلزله را با زیاد شدن فاصله از مرکز زمین لرزه نشان می دهد. یا مقیاس برای اندازه گیری قدرت اسیدی یک محلول، مقیاسی لگاریتمی است. مقدار ( یعنی پتانسیل هیدروژن ) محلول، لگاریتم طبیعی عکس غلظت یون هیدرونیم، است. نکته ای در مورد نماد گذاری: در بیشتر کتاب های درسی و ماشین حساب ها از ، برای نمایش استفاده می کنند. جدول انتگرال توابع لگاریتمی:
خلاصه تبدیل لاپلاس و مباحث وابسته
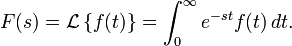
تعریف ریاضی تبدیل لاپلاسلازم به ذکر است که این تبدیل یک تابع را از فضای حقیقی (متغیر t) به فضای مختلط (متغیر s) میبرد.در زیر تبدیل لاپلاس های معروف و همچنین پرکاربردترین ویژگی های تبدیل لاپلاس را ارائه میدهم.تذکر1:منظور از (Dirac(t,n مشتق nام تابع ضربه یا همان دیراک(دلتا) است که در نتیجه n=0 همان تابع ضربه است.تذکر2:تمامی توابع خطی چند جمله ای از عبارت دومی ساخته میشوند مثلاً تابع پله(هوی ساید) همان n=0 است.دانلود جدول تبدیل لاپلاسفرمولهای عمومیتوابع توانیتوابع نماییتوابع هیپربولیکتوابع لگاریتمیتوابع مثلثاتیتوابع خطاتوابع بسل
مقاله ها و نکات کوتاه و بلند ریاضی
صفحه اصلی وبلاگ (آدرس جدید http://www.ep-math.coo.ir/) دانلود مقاله های تخصصی ریاضیدر این قسمت، جدولهایی را مشاهده خواهید کرد که مربوط به شاخه های مختلف ریاضی است. در هر جدول، مقاله های تخصصی مربوط به آن رشته و نیز خلاصه ای از موضوع مقاله را مشاهده خواهید کرد و در کنار آن محلی برای دانلود مقاله در نظر گرفته شده است. اگر متن مقاله به زبان فارسی باشد، خلاصه آن نیز به زبان فارسی و در غیر اینصورت، خلاصه مقاله به زبان انگلیسی است . تاکنون ۳ مقاله در این جداول گنجانده شده است که به مرور تکمیل خواهد شد، انشاءالله. نکات کوتاه و بلند ریاضیاین قسمت مخصوص مقاله ها و نکات نسبتاْ کوتاه ریاضی در سطح دانشجویان کارشناسی و کارشناسی ارشد ریاضی است. فهرست نکات را در زیر هر بخش، خواهید دید. برای مطالعه یا دانلود مقالات، روی تیتر هر بخش کلیک کنید. نظریه اعداد: شامل ۶ نکته۱. آخرین قضییه فرما برای مکعبها۲. صورت کوتاهی از اثبات آخرین قضیه فرما۳. اثبات دیگری برای قضیه کوچک فرما۴. برهان سلبرگ برای قضیه اعداد اول۵. متن کامل مقاله مهم «اندرو وایلز» (سال ۱۹۹۵) در اثبات قضیه آخر فرما۶. اثبات متعالی بودن دو عدد پی و e ریاضی عمومی: شامل ۹ نکته۱. اثبات اصم بودن عدد پی۲. اثبات اصم بودن عدد e۳. بررسی ریشه های مشتق یک تابع به وسیله قضیه آخر فرما۴. فرمولهایی برای محاسبه عدد پی۵. مجموع توانهای k ام اعداد طبیعی 1، 2،...،n۶. دوازده مقاله کوتاه و جالب پیرامون عدد پی۷. جدول مشتق توابع۸. جدول بزرگ انتگرالهای توابع۹. حل معادلات درجه اول تا چهارم جبر: شامل ۷ نکته۱. کوچکترین چندجمله ای که ریشه آن مجموع ریشه های دوم چند عدد است.۲. اثبات ساده ای از قضیه "کوهن"۳. خاصیت "رول" در میدانهای متناهی۴. حلقه هایی بدون ایده آل ماکزیمال۵. طبقه بندی گروهها از مرتبه ۶۶. گروه متناوب A 4 ، دارای مرتبه ای برابر با ۱۲ است اما زیرگروهی از مرتبه ۶ ندارد.۷. ارتباطی بین نظریه گروهها و نظریه حلقه ها جبر خطی: شامل ۱ نکته۱. از دترمینان تا ماتریس آنالیز ریاضی: شامل ۷ نکته۱. اویلر مقدار تابع زتا در نقطه ۲ را چگونه حساب کرد؟۲. مقاله زیبایی پیرامون تابع زتا۳. عدد ثابت اویلر۴. کران بالا و پایین برای ریشه های یک چند جمله ای با ضرایب مختلط۵. آشنایی با روش پوشش تمام در آنالیز حقیقی۶. نکاتی پیرامون مثبت بودن مشتق یک تابع پیوسته و یکنوایی آن۷. برهانهای دیگری برای چند قضیه آنالیز مقدماتی
تابع-حد مشتق
در ریاضیات، یک تابع رابطهای است که هر متغیر دریافتی خود را به فقط یک خروجی نسبت میدهد. علامت استاندارد خروجی یک تابع f به همراه ورودی آن، x میباشد یعنی f(x). به مجموعه ورودیهایی که یک تابع میتواند داشته باشد دامنه و به مجموعه خروجیهایی که تابع میدهد برد میگویند.برای مثال عبارت f(x) = x2 نشان دهنده یک تابع است، که در آن f مقدار x را دریافت میکند و x2 را میدهد. در این صورت برای ورودی 3 مقدار 9 به دست میآید. برای مثال، برای یک مقدار تعریف شده در تابع f میتوانیم بنویسیم، f(4) = 16.معمولاً در تمارین ریاضی برای معرفی کردن یک تابع از کلمه f استفاده میکنیم و در پاراگراف بعد تعریف تابع یعنی f(x) = 2x+1 را مینویسم و سپس f(4) = 9. وقتی که نامی برای تابع نیاز نباشد اغلب از عبارت y=x2 استفاده میشود.وقتی که یک تابع را تعریف میکنیم، میتوانیم خودمان نامی به آن بدهیم، برای مثال:.یکی از خواص تابع این است که برای هر مقدار باید یک جواب وجود داشته باشد، برای مثال عبارت:یک تابع نمیباشد، زیرا ممکن است برای یک مقدار دو جواب وجود داشته باشد. جذر عدد 9 برابر 3 است و در این رابطه اعداد +3 و -3 به دست میآیند. برای ساختن یک تابع ریشه دوم، باید فقط یک جواب برای آن وجود داشته باشد، یعنی:,که برای هر متغیر غیرمنفی یک جواب غیرمنفی وجود دارد.در یک تابع لزومی ندارد که حتماً بر روی عدد علمیاتی انجام گیرد. یک مثال که نشان میدهد که عملیاتی بر روی عدد انجام نمیشود، تابعی است که پایتخت یک کشور را معین میکند. مثلاً Capital(France) = Paris.حال کمی دقیقتر میشویم اما هنوز از مثالهای خودمانی استفاده میکنیم. A و B دو مجموعه هستند. یک تابع از A به B با به هم پیوستن مقادیر منحصر به فرد درون A معین میشود و مجموعه B به دست میآید. به مجموعه A دامنه تابع میگویند؛ مجموعه B هم تمام مقادیری را که تابع میتواند داشته باشد شامل میشود.در بیشتر زمینههای ریاضی، اصطلاحات تبدیل و نگاشت معمولاً با تابع هم معنی پنداشته میشوند. در هر حال ممکن است که در بعضی زمینههای خصوصیات دیگری داشته باشند. برای مثال در هندسه، یک نگاشت گاهی اوقات یک تابع پیوسته تعریف میشود.تعاریف ریاضی یک تابعیک تابع f یک رابطه دوتایی است، به طوری که برای هر x یک و فقط یک y وجود داشته باشد تا x را به y رابطه دهد. مقدار تعریف شده و منحصر به فرد y با عبارت (f(x نشان داده میشود.به دلیل اینکه دو تعریف برای رابطه دوتایی استفاده میشود، ما هم از دوتعریف برای تابع استفاده میکنیم.تعریف اولساده تعریف رابطه دوتایی عبارتست از: «یک رابطه دوتایی یک زوج مرتب میباشد». در این تعریف اگر رابطه دوتایی ...
رياضي سمستر اول
اعمال هفت گانه اعمال اربعه در حساب یا ریاضی عبارت است از عملیه جمع، تفریق، ضرب، تقسیم، در صورتیکه توان (طاقت) جذر و لوگاریتم را با آنها علاوه کنیم میتوان از اعمال هفت گانه در ریاضی نام برد. در حالت ضرب نمودن یک عدد به 1000 و 100 و 10 و غیره به آ ساني تعداد صفر هاي نضروب را در مقا بل مضروب فيه علا وه مينما يم. بر خلاف هر گاه يك عددراتقسيم 10، 100، 1000 و غیره نمائیم تعداد صفرهای این اعداد (مقسوم علیه) از عدد مقسوم اعشاری را از راست به چپ جدا مینمائیم: 1-1 کسرعام عبارت از نسبت بین دو عددیست که آنها را به نام صورت و مخرج یاد میکنند. به عباره ساده کسر نشان میدهد که یک عدد به چند حصه تقسیم گردیده و چند حصه آن گرفته شده است. برای دریافت کردن حاصل جمع و تفریق کسر عام کوچکترین مخرج مشترک مخرج ها را بدست می آوریم، درینجا مقصد از کوچکترین مخرج مشترک بدست آوردن ذواضعاف اقل مخرج ها می باشد. یعنی کوچکترین عددی را بدست می آوریم که به تمام مخرج ها پوره قابل تقسیم باشد. 1-1-1 ضرب کسر عام: در ضرب کسر عام بعد از اختصار در صورتیکه قابل اختصار باشند صورت ها با هم و مخرج ها را با هم ضرب میکنیم. 2-1-1 تقسیم کسرعام: در تقسیم کسر عام کسر مقسوم را نوشته ضرب در عکس کسر مقسوم علیه مینمائیم. در صورتیکه کسرها دارای اعداد صحیح هم باشند اولتر از همه لازم است که آنها را بدون عدد صحیح نمائیم. یاد داشت: بخاطر باید داشت که: 1) در یک کسر اگر صورت بزرکتر از مخرج باشدف کسر مربوط بزرگتر از (1) است. 2) در یک کسر هرگاه مخرج بزرگتر از صورت باشد، کسر مربوط کوچکتر از (1) است. 3) در یک کسر اگر صورت مساوی به صفر باشد، کسر مربوط مساوی به صفر است. 4) در صورتیکه مخرج یک کسر صفر باشد، کسر مذکور مساوی به است. 2-1 کسر اعشاری: هرگاه یک واحد نام به 10و100و1000 و غیره طاقت های 10 تقسیم گردد و از آن چند حصه گرفته بوشد، این نوع کسور را بنام کسرهای اعشاری یاد میکند. مثلاً 0.25 این معنی را میدهد که واحدهای مربوط به 100 تقسیم گردیده و از آن 25 حصه گرفته شده است. 1-2-1 جمع اعداد اعشاری: در جمع اعداد اعشاری اعداد را طوری در تحت همدیگر می نویسیم که علامه های اعشاری در یک ستون قرار گیرد و بعداً مانند جمع ساده عملیه را تا اخیر انجام میدهیم. فرق بین جمع ساده و اعشاری این است که همین که به ستون اعشاری رسیدیم علامه اعشاری را در تحت ستون نقل میدهیم. مثال: 2-2-1 تفریق اعداد اعشاری: در عملیه تفریق اعداد اعشاری نیز عین عملی را که در عملیه جمع انجام دادیم اجرای مینمائیم، ولی در اینجا باید مقدم تر عدد بزرگ و بعداً عدد کوچک تعریف گردد. مثال: 3-2-1 ضرب اعداد اعشاری: در ...
لگاریتم
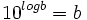
مقدمه در جبر عموما لگاریتم معمولی یا لگاریتم در پایه 10 عدد b را توانی تعریف میکنند که 10 باید به آن برسد تا b بدست آید: . فرض کنیم چنین عددی موجود بوده و از لگاریتمها برای سادهکردن ضرب اعدادی که ارقام اعشاری زیادی دارند استفاده میکنیم. تعریف تابع لگاریتم طبیعی بصورت زیر نمایش داده میشود: به ازای هر x بزرگتر از 1 ، این انتگرال مساحت ناحیهای را نشان میدهد که از بالا به خم از پایین به محور t از طرف چپ به خط t=1 ، و از طرف راست به خط t=x محدود است. تاریخچه در اواخر قرن شانزدهم یک بارون اسکاتلندی به نام جان نپر (1550-1617) ابزاری بنام لگاریتم ابداع کرد که با تبدیل ضرب به جمع کار محاسبه را ساده میکند؛ یعنی داریم: لگاریتم x + لگاریتم a = لگاریتم ax برای ضرب دو عدد مثبت x,a از یک جدول ، لگاریتمهای x,a را پیدا میکنیم، سپس این لگاریتمها را بهم میافزائیم مجموع حاصل را در داخل جدول مییابیم، و بالاخره حاصلضرب مطلوب ax را از حاشیه جدول میخوانیم. مسلما در دست داشتن جدول کلید کار بود، به همین سبب نپر در دو دهه آخر زندگیاش را صرف تهیه جدولی کرد که هیچگاه نتوانست آن را تمام کند. و این در حالی بود که تیکو براهه ستاره شناس ، مشتاقانه در انتظار این جدول بود تا میتواند محاسبات خودش را تسریع بخشد مشتق تابع لگاریتم طبیعی چون تابع با انتگرال ذکر شده در قسمت تعریف ، تعریف میشود، فورا از نخستین قضیه اساسی حساب دیفرانسیل و انتگرال نتیجه میشود که مشتق تابع برابر خواهد بود. بنابراین اگر u تابع مشتقپذیری از x باشد، آنگاه از قاعده زنجیری داریم: فرمول کلیتر زیر بدست میآید: مشتقگیری لگاریتمی گاهی یک تابع با معادلهای پیچیده داده شده با گرفتن لگاریتم از طرفین آن پیش از مشتقگیری میتوان مشتقش را سریعتر حساب کرد. خواص قلمرو: مجموعه تمام اعداد حقیقی مثبت ، x>0 برد: مجموعه تمام اعداد حقیقی این تابع بر قلمرو خود پیوسته و صعودی است هر گاه آنگاه . این تابع یک تابع یکبهیک از قلمرو خود به بردش است، بنابراین دارای معکوس است. حاصلضرب ، خارج قسمت و توان: هر گاه x,a دو عدد مثبت باشند. آنگاه:معکوس تابع لگاریتم چون یکبهیک و مشتقپذیر است، دارای معکوس مشتقپذیر میباشد نمودار منعکس نمودار تابع نسبت به خط y=x است. این نمودار تابع نیز میباشد. تابع به ازای هر عدد حقیقی x مساوی میباشد. تابع حاصل تابع مشتق پذیری از x است که به ازای هر x حقیقی تعریف شده است و بعنوان تابع نمایی از آن یاد میشود که e را پایه و x نما خوانده میشود. همچنین توجه میکنیم که حد تابع نمایی زمانی که x بسمت بینهایت میل میکند برابر بینهایت است و زمانی ...
فرمولهای مشتق
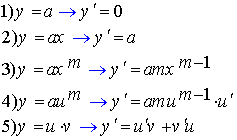
مشتق توابع معکوس مثلثاتیمشتق توابع نماییمشتق تابع مرکب و قدر مطلق
