جدول تانژانت زاویه ها
توابع مثلثاتی
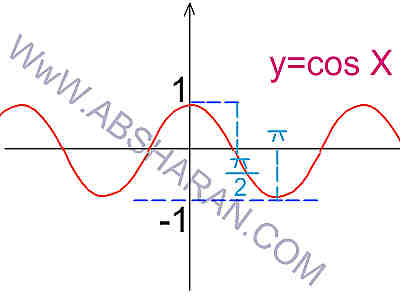
تابع مثلثاتی Cos نیز یکی از توابع مهم مثلثاتی است.همانطور که از نمودارد تابع مثلثاتی Cos پیداست,این تابع یک تابع زوج است (نسبت به محور Y قرینه است).دامنه ی تابع مثلثاتی Cos مجوعه ی اعداد حقیقی و برد این تابع مثلثاتی اعداد بین 1 و 1- می باشند.یعنی مقدار از 1 بیشتر و از 1- کمتر نمی شود.نمودار تابع Cos بصورت زیر است: با توجه به نمودار تابع مثلثاتی Cos این تابع نیز یک به یک نمی باشد.از آنجاییکه تابع Cos یک تابع زوج است پس رابطه ی زیر برقرار می باشد: آموزش مثلثات,تابع مثلثاتی سینوس Sin یکی از توابع پرکاربرد مثلثاتی است.همانطور که از نمودار تابع مثلثاتی سینوس پیداست,این تابع یک تابع فرد است (نسبت به مبداء مختصات قرینه است).دامنه ی تابع مثلثاتی سینوس sin مجوعه ی اعداد حقیقی و برد این تابع مثلثاتی اعداد بین 1 و 1- می باشند.یعنی مقدار سینوس از 1 بیشتر و از 1- کمتر نمی شود.نمودار تابع Sin سینوس بصورت زیر است: با توجه به نمودار تابع مثلثاتی سینوس Sin این تابع یک به یک نیز نمی باشد.از آنجاییکه تابع سینوس یک تابع فرد است پس رابطه ی زیر برقرار می باشد: Y=Sin(-X)=-SinX آموزش مثلثاتدر ابتدای آموزش مثلثات به بررسی دایره ی مثلثاتی می پردازیم,دایره ی مثلثاتی شما را در یافتن مقادیر زاویه ها در مثلثات یاری می کند.: هر دایره دارای یک مبداء بوده که شروع حرکت متحرک از آن جا آغاز می گردد,دارای 4 ناحیه می باشد,دارای جهت اصلی خلاف عقربه های ساعت (جهت مثبت) می باشد.دارای 4 محور است که محور سینوس Sin و تانژانت tg موازی هم و محور Cos و کتانژانت Cotg در دایره ی مثلثاتی موازی هم هستند. تغییرات sin و cos بین 1 و 1- و تغییرات تانژانت tg و cotg از تا است. روش محاسبه ی نسبت های مثلثاتی: برای محاسبه ی sin و cos یک زاویه انتهای کمان را بر محور Sin و یا cos عمود می کنیم,ولی برای محاسبه ی tg و یا cotg یک زاویه انتهای کمان را امتداد داده تا محور tg و یا cotg را قطع کند. اگر x زاویه ای در ناحیه ی اول باشد,در ناحیه ی اول تمام نسبت های مثلثاتی مثبت است. اگر x در ناحیه ی دوم باشد فقط سینوس sin مثبت است. اگر x در ناحیه ی سوم باشد در ناحیه ی سوم سینوس sin و cos منفی و تانژانت tg و کتانژانت cotg مثبت است. اگر x در ناحیه ی چهارم باشد,در ناحیه ی چهارم فقط cos مثبت است. ده رابطه ی مهم مثلثاتی: ================================================================================================ نسبت های مثلثاتی کمان 2x : ============================================================================= نسبت های مثلثاتی زوایای 3x : ================================================================================================= نکته: ==================================================================================================== چند نسبت دیگر: ================================================================================================== فرمول ...
توابع اکسل
238 تابع در اکسل وجود دارد که در این جا آنها را معرفی می نماییم.عملکردنام تابعمقدار حقیقی عدد را باز می گرداند، عددی بدون علامتش.ABS----------------------------------------
پیدایش مثلثات
تاریخ علم به آدمی یاری می رساند تا «دانش» را از «شبه دانش» و «درست» را از «نادرست» تشخیص دهد و در بند خرافه و موهومات گرفتار نشود. در میان تاریخ علم، تاریخ ریاضیات و سرگذشت آن در بین اقوام مختلف ، مهجور واقع شده و به رغم اهمیت زیاد، از آن غافل مانده اند. در نظر داریم در این فضای اندک و در حد وسعمان برخی از حقایق تاریخی( به خصوص در مورد رشته ریاضیات) را برایتان روشن و اهمیت زیاد ریاضی و تاریخ آن را در زندگی روزمره بیان کنیم.برای بسیاری از افراد پرسش هایی پیش می آید که پاسخی برای آن ندارند: چه شده است که محیط دایره یا زاویه را با درجه و دقیقه و ثانیه و بخشهای شصت شصتی اندازه می گیرند؟ چرا ریاضیات با کمیت های ثابت ادامه نیافت و به ریاضیات با کمیت های متغیر روی آوردند؟ مفهوم تغییر مبناها در عدد نویسی و عدد شماری از کجا و به چه مناسبت آغاز شد؟ یا چرا در سراسر جهان عدد نویسی در مبنای ۱۰ را پذیرفته اند، با اینکه برای نمونه عدد نویسی در مبنای ۱۲ می تواند به ساده تر شدن محاسبه ها کمک کند؟ ریاضیات از چه بحران هایی گذشته و چگونه راه خود را به جلو گشوده است؟ چرا جبر جانشین حساب شد، چه ضرورت هایی موجب پیدایش چندجمله ای های جبری و معادله شد؟ و... برای یافتن پاسخ های این سئوالات و هزاران سئوال مشابه دیگر در کلیه رشته ها، تلاش می کنیم راه را نشان دهیم، پیمودن آن با شماست...● پیدایش مثلثاتاز نامگذاری «مثلثات» می توان حدس زد که این شاخه از ریاضیات دست کم در آغاز پیدایش خود به نحوی با «مثلث» و مسئله های مربوط به مثلث بستگی داشته است. در واقع پیدایش و پیشرفت مثلثات را باید نتیجه ای از تلاش های ریاضیدانان برای رفع دشواری های مربوط به محاسبه هایی دانست که در هندسه روبه روی دانشمندان بوده است. در ضمن دشواری های هندسی، خود ناشی از مسئله هایی بوده است که در اخترشناسی با آن روبه رو می شده اند و بیشتر جنبه محاسبه ای داشته اند. در اخترشناسی اغلب به مسئله هایی بر می خوریم که برای حل آنها به مثلثات و دستورهای آن نیازمندیم. ساده ترین این مسئله ها، پیدا کردن یک کمان دایره(بر حسب درجه) است، وقتی که شعاع دایره و طول وتر این کمان معلوم باشد یا برعکس، پیدا کردن طول وتری که طول شعاع دایره و اندازه کمان معلوم باشد. می دانید سینوس یک کمان از لحاظ قدر مطلق برابر با نصف طول وتر دو برابر آن کمان است. همین تعریف ساده اساس رابطه بین کمان ها و وترها را در دایره تشکیل می دهد و مثلثات هم از همین جا شروع شد.کهن ترین جدولی که به ما رسیده است و در آن طول وترهای برخی کمان ها داده شده است متعلق به هیپارک، اخترشناس سده دوم میلادی است و شاید بتوان تنظیم این جدول ...
تاریخچه ی توابع مثلثاتی
مثلثات از درون هندسه در آمد و بیش از همه،ریاضیدانان ایرانی روی آن کار کردند.بررسی های اخترشناسی در بابل قدیم و یونان، ریاضیدانان را به سمت موضوع هایی کشانید که می توان آن را پیش درآمد مثلثات دانست."آریستارک" و "اراتستن" دو دانشمند مقیم اسکندریه در سده سوم پیش از میلاد،از مفهوم های نخستین مثلثات یاری می جستند.ارشمیدس-دانشمند بزرگ یونانی-(287 تا 212 پیش از میلاد)،ضمن بررسی هایی درباره ی دایره،برای محاسبه ی وترها و یافتن دستورهایی برای جمع و تفریق کمان ها،تلاش هایی کرد."هیپارک" اخترشناس یونانی میانه های سده دوم میلادی،تقسیم دایره را به شیوه بابلی ها پذیرفت و جدولی تنظیم کرد که در آن برخی وترها از روی کمان آن ها محاسبه شده بود."منلائوس"و"بطلمیوس"در سده ی دوم میلادی هم،کارهایی در این زمینه دارند ولی دانشمندان یونانی که به ویژه روی هندسه کار می کردند،وتر کمان ها را به کار می بردند و نتوانستند به خطهای مثلثاتی دست یابند.در واقع نخستین تابع های مثلثاتی را باید جدول وترها بر حسب کمان آن ها دانست که برای محاسبه های اخترشناسی لازم بود و در دو سده ی پیش از میلاد به وجود آمد.برای نخستین بار دانشمندان هندی در فاصله زمانی از سده پنجم تا دوازدهم میلادی از "نیم وتر" به جای وتر استفاده می کردند که متناظر با مفهوم سینوس امروزی است.آن ها نیم وتر را "اردهاجیا"(یا"جیا اردها") می گفتند که از لحاظ لغوی به معنای نصف وتر است.به تدریج اردهاجیا را کوتاه کردند و "جیا" نامیدند.به جز این،هندی ها از یک منهای کسینوسx هم استفاده می کردند و آن را "کوماجیا" می نامیدند و مقدار cosx را "کوتی جیا" می گفتند."ابوالوفای بوزجانی"(940 تا 988 میلادی)ریاضیدان ایرانی(ویرانه های بوزجان نزدیک تربت جام است)،تانژانت را به نام "ظل" وارد مثلثات کرد و جدولی را تنظیم کرد که 30دقیقه به 30دقیقه مقدار سینوس ها را تعیین می کرد.دستورهای sin a+b و sin a-b را کشف کرد و برخی از مساله های مثلثات کروی را حل نمود.اما گام اصلی را نصیرالدین طوسی برداشت.تالیف او به نام"کشف القناع فی اسرار شکل القطاع"در واقع نخستین کتاب درباره مثلثات است.نقش طوسی را در مثلثات،باید شبیه نقش اقلیدس در هندسه دانست..زیرا او توانست مجموعه ی آن چه را که پیش از او وجود داشت،به صورت دانشی مستقل و منظم درآورد.ترجمه ای از کتاب طوسی در سال 1891 به زبان فرانسوی انجام گرفت و تا مدت ها به عنوان کتاب درسی،مورد استفاده ی دانش پژوهان در اروپای غربی بود.سینوس را به زبان عربی"جَیب"به معنای"گریبان"می گفتند که به همان معنا به زبان فرانسوی برگردانده شد."سینوس" یعنی گریبان.به همین مناسبت،برخی معتقدند که خوارزمی یا هم عصران او،"سینوس" ...
فرمول های ریاضی و مثلثاتی اکسل
به جدول زير توجه كنيد: نام تابع شرح تابع مثالABS قدر مطلق یک عدد را می دهد. =(ABS -2)ACOS Arcos یک عدد را می دهد. (رادیان) =(ACOS(-0.5)*180/PI)ACOSH آرک کوسینوس هیپربولیک =(ACOSH 10)ATAN2 Arctan نقطه ای به مختصات X,Y را روی دایره مثلثاتی می دهد.(تبدیل به درجه *180/(pi) =(ATAN2 -1, -1)CEILING عددی را به مقداری بالاتر ،نسبت به صف روند می کند ، که این مقدار ضریب عددی است که پارامتر دوم تابع است. =(CEILING2.4;2)FLOOR عددی را به مقداری پایین تر از خودش، نسبت به صف روند می کند، که این مقدار ضریب عددی است که پارامتر دوم تابع است. COMBIN احتمال ترکیب ریاضی دو عدد =(COMBIN 4;2)COUNTIF تعداد خانه هایی که دارای شرط خاصی هستند را می دهد. =(COUNTIFB2:B5,">55")DEGREES رادیان را به درجه تبدیل می کند.توجه : تمام فرمولها برحسب رادیان هستند. =((DEGREES(PI)EVEN عددی را به نزدیکترین عدد زوج بعداز خودش گرد می کند. =(EVEN 2.5)EXP عدد e را به توان x می رساند. =(EXP1)FACT فاکتوریل یک عدد را محاسبه می کند. (N!) =(FACT3)FACTDOUBLE اگر n زوج : n!!=n(n-2)(n-4)…(4)(2)اگر n فرد : n!!=n(n-2)(n-4)…(3)(1) =(FACTDOUBLE(6GCD بزرگترین مقسوم علیه مشترکGreatest Common Divisor =GCD(24, 36) à12INR جزء صحیح یک عدد را میدهد. =INT(5.4) à 5LCM کوچکترین مضرب مشترکLeast Common Multiple =LCM(36;24) à 72LN لگاریتم در مبنای e =LN(2.7182818) à 1LOG لگاریتم در مبنای 10 یا دلخواه =LOG(8;2) à 3LOG10 لگاریتم در مبنای 10 =LOG10(10^5) à 5MDETERM دترمینال یک ماتریس (بردار) را میدهد. =MDETERM({3,6;1,1})à -3MINVERSE P ماتریس معکوس را میدهد =(MINVERSEA2:C4) à PMMULT P حاصلضرب دو ماتریس را میدهد. =(MMULT array1;aray2) àPMOD باقی مانده تقسیم دو عدد برهمMOD(n, d) = n - d*INT(n/d) =MOD(10;3) à1MROUND عددی را به مضربی دلخواه از عدد دیگر، گرد میکند. =MROUND(10;3) à9MULTINOMIA نسبت فاکتوریل جمع به فاکتوریل حاصلضرب= (a+b+c)! / a! b! c! =MULTINOMIAL(2,3,4)à1260ODD عددی را به نزدیکترین عدد فرد بعد از خودش گرد میکند. =ODD(1.5) à 3PI() عدد پی را میدهد. =PI() à3.14159265358979POWER عدد را به توان داده شده میرساند. =POWER(2;10) à1024PRODUCT حاصلضرب اعداد =PRODUCT(2,3,5) à 30QUOTIENT خارج قسمت یک تقسیم را میدهد. =QUOTIENT(15;3) à 5RADIANS درجه را به رادیان تبدیل میکند. =RADIANS(90) à1.570796RAND() N عددی تصادفی بین 0 تا 1 تولید میشود. =RAND()*(b-a)+a=TRUNC(RAND()*100(RANDBETWEENN@ عددی تصادفی بین محدوده ورودی داده شده میدهد. =RANDBETWEEN(1,100)ROMAN اعداد را به اعداد یونانی تبدیل میکند. =ROMAN(8) à VIIIROUND برای گرد کردن اعداد با دقت در تعداد رقم اعشار =ROUND(2.15;1) à 2.1ROUNDDOWN گرد کردن اعداد به سمت صفر =ROUNDDOWN(2.578;2)à2.57ROUNDUP گرد کردن اعداد دور از صفر =ROUNDUP(2.578;2)à2.58SERIESSUM تابع SERIES را میدهد . ر.ک به راهنمای اکسل SIGN علامت یک تابع را میدهد. (مثبت 1 منفی 0 ) =SING(-5) à 0SIN مقدار سینوس یک زاویه (رادیان) را میدهد. =SIN(30*(PI)/180) à 0.5SINH مقدار سینوس هیپربولیک را میدهد. SQRT محاسبه جذر یک ...
تابع های مثلثاتی
بررسی های اخترشناسی، در بابل قدیم و یونان، ریاضی دانان را به سمت موضوع هایی کشانید که می توان آن را پیش درآمد مثلثات دانست. "اریستاک" و "اراتوستن" دو دانشمند مقیم اسکندریه در سده سوم پیش از میلاد، از مفهوم های نخستین مثلثات یاری جستند. ارشمیدس دانشمند بزرگ یونانی، ضمن بررسی هایی درباره دایره، برای محاسبه وترها و یافتن دستورهایی برای جمع و تفریق کمان ها، تلاش هایی کرد. "هیپارک" اخترشناس یونانی تقسیم دایره را به شیوه بابلی ها پذیرفت و جدولی تنظیم کرد که در آن، برخی وترها از روی کمان آن ها محاسبه شده بود. "منلائوس" و "بطلمیوس" هم کارهایی در این زمینه دارند. ولی دانشمندان یونانی که به ویژه روی هندسه کار می کرند وتر کمان ها را به کار می بردند و نمی توانستند به خط های مثلثاتی دست یابند. در واقع نخستین تابع های مثلثاتی را باید جدول وترها برحسب کمان های آن ها دانست که برای محاسبه ای اخترشناسی لازم بود و در دو سده پیش از میلاد به وجود آمد. خسته که نشدید؟؟ از این جا به بعدش جالب تره....تا حالا به معنی سینوس، کسینوس، تانژانت و کتانژانت فکر کرده بودید؟؟؟؟ برای نخستین بار دانشمندان هندی از "نیم وتر" به جای وتر استفاده کردند که متناسب با مفهوم سینوس امروزی است. آن ها نیم وتر را "اردهاجیا" ( یا جیااردها) می گفتند که به معنای نصف وتر است (خوبه یه کلمه هندی هم یاد گرفتیم!). به تدریج اردهاجیا را کوتاه کردند و "جیا" نامیدند. به جز این هندی ها از (1-cosx)هم استفاده كردند و آن را"کوماجیا" نامیدند، مقدارcosx را "کوتی جیا" می گفتند. ابوالوفای برازجانی ریاضی دان ایرانی، تانژانت را به عنوان "ظل" وارد مثلثات کرد و جدولی برای سینوس ها تنظیم کرد که 30 دقیقه به 30 دقیقه مقدار سینوس ها را معین می کرد ( ساعت نبوده ها!!!). دستورهای (sin (a + b) , sin (a – b را کشف کرد و برخی مساله های مثلثات کروی را حل کرد. اما گام اصلی را نصیرالدین طوسی برداشت. تالیف او به نام "کشف القناع فی اسرار شکل القطاع" در واقع نخستین کتاب درباره مثلثات است. نقش طوسی را در مثلثات باید شبیه نقش اقلیدس در هندسه دانست. زیرا او توانست مجموعه آنچه را که پیش از او وجود داشت، به صورت دانشی مستقل و منظم درآورد. ترجمه ای از کتاب طوسی به زبان فرانسوی انجام گرفت و تا مدت ها به عنوان کتاب درسی مورد استفاده دانش پژوهان در اروپای غربی بود. سینوس را به زبان عربی "جیب" به معنی گریبان می گفتند که به همان معنا به زبان فرانسه برگردانده شد. سینوس یعنی گریبان و به همین مناسبت برخی معتقدند خوارزمی یا هم عصران او، سینوس را "جیپ" می نامیدند که واژه ای پهلوی و به معنای "دیرک" است. ( این دیرک، خودش یه داستان داره که...به ...
پیدایش مثلثات

تاریخ علم به آدمی یاری می رساند تا «دانش» را از «شبه دانش» و «درست» را از «نادرست» تشخیص دهد و در بند خرافه و موهومات گرفتار نشود. در میان تاریخ علم، تاریخ ریاضیات و سرگذشت آن در بین اقوام مختلف ، مهجور واقع شده و به رغم اهمیت زیاد، از آن غافل مانده اند. در نظر داریم در این فضای اندك و در حد وسعمان برخی از حقایق تاریخی( به خصوص در مورد رشته ریاضیات) را برایتان روشن و اهمیت زیاد ریاضی و تاریخ آن را در زندگی روزمره بیان كنیم. برای بسیاری از افراد پرسش هایی پیش می آید كه پاسخی برای آن ندارند: چه شده است كه محیط دایره یا زاویه را با درجه و دقیقه و ثانیه و بخش های شصت شصتی اندازه می گیرند؟ چرا ریاضیات با كمیت های ثابت ادامه نیافت و به ریاضیات با كمیت های متغیر روی آوردند؟ مفهوم تغییر مبناها در عدد نویسی و عدد شماری از كجا و به چه مناسبت آغاز شد؟ یا چرا در سراسر جهان عدد نویسی در مبنای ۱۰ را پذیرفته اند، با اینكه برای نمونه عدد نویسی در مبنای ۱۲ می تواند به ساده تر شدن محاسبه ها كمك كند؟ ریاضیات از چه بحران هایی گذشته و چگونه راه خود را به جلو گشوده است؟ چرا جبر جانشین حساب شد، چه ضرورت هایی موجب پیدایش چندجمله ای های جبری و معادله شد؟ و… برای یافتن پاسخ های این سئوالات و هزاران سئوال مشابه دیگر در كلیه رشته ها، تلاش می كنیم راه را نشان دهیم، پیمودن آن با شماست… ● پیدایش مثلثاتاز نامگذاری «مثلثات» می توان حدس زد كه این شاخه از ریاضیات دست كم در آغاز پیدایش خود به نحوی با «مثلث» و مسئله های مربوط به مثلث بستگی داشته است. در واقع پیدایش و پیشرفت مثلثات را باید نتیجه ای از تلاش های ریاضیدانان برای رفع دشواری های مربوط به محاسبه هایی دانست كه در هندسه روبه روی دانشمندان بوده است.در ضمن دشواری های هندسی، خود ناشی از مسئله هایی بوده است كه در اخترشناسی با آن روبه رو می شده اند و بیشتر جنبه محاسبه ای داشته اند. در اخترشناسی اغلب به مسئله هایی بر می خوریم كه برای حل آنها به مثلثات و دستورهای آن نیازمندیم. ساده ترین این مسئله ها، پیدا كردن یك كمان دایره (بر حسب درجه) است، وقتی كه شعاع دایره و طول وتر این كمان معلوم باشد یا برعكس، پیدا كردن طول وتری كه طول شعاع دایره و اندازه كمان معلوم باشد. می دانید سینوس یك كمان از لحاظ قدر مطلق برابر با نصف طول وتر دو برابر آن كمان است. همین تعریف ساده اساس رابطه بین كمان ها و وترها را در دایره تشكیل می دهد و مثلثات هم از همین جا شروع شد.كهن ترین جدولی كه به ما رسیده است و در آن طول وترهای برخی كمان ها داده شده است متعلق به هیپارك، اخترشناس سده دوم میلادی است و شاید بتوان تنظیم این جدول ...
انواع پیچ و مهره

شرح انواع مختلف پیچها:در بیشتر واحدهای صنعتی از پیچ ها برای سوار کردن و اتصال قطعات روی یکدیگر و نیز تنظیم دستگاههای صنعتی و یا جهت انتقال حرکت استفاده می شود. در کمتر دستگاهی است که از پیچها استفاده نمیشود بهمین دلیل است که اهمیت آنها در صنعت بسیار زیاد میباشد. مواردیکه از پیچها استفاده میشود عبارتند از:ماشینهای ابزار، انواع گیره ها، وسائط نقلیه، ابزرار و ادوات جنگی و کشتی ها، هواپیماها، ساختمانهای فلزی، میز و صندلی، ماشینهای چاپ و ریسندگی و بافندگی.تراشیدن پیچها بوسیله ماشین تراش و یا سایر دستگاههای دیگری نیز صورت میگیرد که البته برحسب نوع دقت و اندازة آن در دستگاه مخصوص بخود تراشیده یا ساخته میشوند.شکل (۱۴۲) تراشیدن پیچ را بوسیله ماشن تراش نشان میدهد که با داشتن مشخصات کامل پیچ و با در نظر گرفتن اصول پیچ تراشی و مراحل آن میتوان آنرا تراشید. ولی بطور کلی تراشیدن پیچ با ماشین تراش بدون شک یکی از مشکلترین عملیاتی است که انجام میگیرد. منظور از تراشیدتن پیچ ایجاد شیار مارپیچی با فرم دندانه و زاویه مشخصی روی محیط استوانه ای ایجاد میگردد میباشد. علاوه بر آن نیز میتوان همین عمل را در داخل سوراخهای داخلی انجام داد.شرح اجزاء مختلف پیچ و طریقه تراشیدن آنها:قبل از اینکه به تراش پیچها اقدام نمائیم لازم است که اجزاء مختلف آنرا بشناسیم برای این منظور بطور خلاصه بشرح هر یک بصورت زیر میپردازیم.۱- قطر خارجی Mujor D – بزرگنرین قطر پیچ و یا مهره را قطر خارجی آن گویند که عبارت است از اندازه سر دندانه تا سر دندانه مقابل که آنرا با حرف OD نمایش میدهند.۲- ارتفاع یا گودی دندانه Depth of T – ارتفاع دندانه عبارت است از فاصله قائم میان سر دندانه تا ته دندانه پیچ که آنرا با علامت h مشخص مینمایند.۳- قطر داخلی Minor D که کوچکترین قطر پیچ و یا مهره را قطر داخلی گویند که اندازه آن عبارت است از فاصله ته دندانه تا ته دندانه مقابل آن یا بعبارت دیگر برابر است با تفاضل قطر بزرگ دو برابر ارتفاع دندانه که با حرف I نشان میدهند. شکل (۱۴۳) اجزاء مختلف پیچ را نشان میدهد.۴- تعداد دندانه Nimber of T. – همانطور که در شکل پیدا است تعداد دندانه عبارت است از تعداد دندانه در یک اینچ روی محیط در طول پیچ که برای تعیین آن خط کش یا کلیس را روی پیچ مطابق شکل قرار داده و سپس دنداغنه های بین یک اینچ را میشماریم که معمولاً آنرا با حرف N نمایش میدهیم. علاوه بر آن میتوان با طرق مختلف دیگری آنرا اندازه گیری نمود که عبارت از استفاده از شابلن باین ترتیب که شابلن مورد نظر را روی دندانه ها قرار داده و در صورتیکه نوری از بین دندانه ها نشاهده نشد تعداد دندانه هائیکه روی شابلن ...
