تبدیلات لورنتس
تبدیلات لورنتس و اثبات کامل
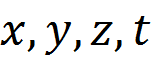
همانطور که مشاهده کردیم ودیدیم تبدیلات گالیله نمی توانند پدیدهای را که سرعت های انها نزدیک سرعت نور است را توصیف کنند وباید معادلتی جایگزین ان ها شوند که با تجربه سازگار است این معادلات را معادلات لورنتس نامیدند علت این نام گذاری همانطور که در بحث قبل دیدم لورنتس اولین کسی بودکه برای حفظ چارچوب اتر فرض اینکه اجسام در راستای حرکتشان کوتاه می شوند را ارائه کرد هرچند اینشتین این تبدیلات را با مفهومی درست تر بدست اورد ولی این معادلات را معادلات لورنتس نامیدند.ما هرچند در این وبلاگ قبلا این معادلات را نوشتیم ولی در این اینجا می خواهیم این معادلات را با استفاده از فرض های ساده کننده که هیچ لطمه ای به کلیت مسئله نمی زند و یک نتایجی صوری بدست می اوریم که بعدا انها را محک می زنیم. رویدادی را رادر نظر بگیریم که در چارچوب S مختصات فضا- زمان ان را به وسیله پارامتر های زیر معلوم می کنیم این رویداد را در چارچوبی که نسبت به S با سرعتی یکنواخت V حرکت می کند یعنی چارچوب 'S با مختصات پریم دار از چهار چوب S تفکیک می کنیم یعنی مختصات فضا –زمانی این رویداد درچارچوب'S به صورت زیر است اکنون ما به دنبال روابطی هستیم که این دو مختصات را بهم ربط دهد که به صورت نماد ریا ضی داریم ما در اینجا از دو اصل یعنی اصل نسبیت و اصل همگن بودن فضا –زمان برای حل مسئله مدد می جوییم همانطور که می دانیم اصل نسبیت خود شامل دو قسم است که به قرار زیر است: 1.هیچ دستگاه لخت مرجع خاصی (مانند اتر شکست خورده) وجود ندارد وقوانین فیزیک باید در تمام چارچوب ها معتبر باشد(مثل پایستگی تکانه خطی در برخورد) 2.سرعت نور در برای تمام چار چوب های لخت یکی باشد دومین اصل که همگنی فضا –زمان می باشد یعنی هیچ نقطه خاصی چه در فضا و چه در زمان وجود نداشته باشد که نسبت به نقاط دیگر متفاوت باشد یعنی تمام فضا _زمان هم ارزند. برای ساده کردن مسئله فرض می کنیم که که دو چارچوب S و'S فقط در امتداد محور X هاست که دارای حرکت نسبی هستند به شکل زیر نگاه کنید این فرض هیچ محدودیتی در نتایج ندارد چرا که فضا همسانگرد است یعنی خواص ان تحت چرخش یکسان است همچنین در لحظه ای که دو مبداء O و'O بر هم منطبق اند ساعت ها را به ترتیب روی صفر تنظیم می کنیم یعنی بعلاوه فرض همگنی فضا ایجاب می کند که روابط بین مختصات فضا –زمانی تنها به صورت خطی باشد یعنی داریم ضرایب بالا با شاخص های نشان داده شده اند که این شاخص ها شاخص های ثابتی هستند وباید معین گردند اکنون می خواهیم این شانزده ضریب را پیدا کنیم انتظار داریم که این شانزده ضریب به سرعت نسبی چارچوب ها یعنی V بستگی داشته باشد یعنی اینکه ...
نسبیت خاص
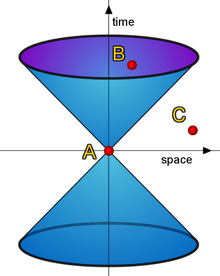
لبته در نظر داشته باشید که هنگامی که c به سمت بی نهایت میل می کند( همانگونه که پیش از اثبات متناهی بودن سرعت نور پنداشته می شد) کسر v/c به سمت صفر میرود. این بدان معناست که تبدیلات لورنتس که اساس نظریهٔ نسبیت خاص هستند در سرعتهای بسیار کم نسبت به نور، نتایج یکسانی را با معادلات گالیله که اساس نسبیت نیوتونی هستند به دست میدهند. نظریه نسبیت خاص به ما می گوید که c تنها سرعت یک پدیده مشخص نیست بلکه یکی از ویژگیهای بنیادی شیوه ای است که فضا و زمان با یکدیگر به شکل فضا زمان یکپارچه گشته اند. یکی از پیامدهای این نظریه است که ذره ای که جرم لختی دارد هرگز سرعتش به سرعت نور نمی رسد. واژه خاص در نسبیت خاص به نشانگر حالت خاصی است که این نظریه در آن صادق است.این نظریه اصل نسبیت را تنها در مورد ویژه چارچوبهای مرجع لخت به کار برده است. به عبارت دیگر این طور پنداشته شده است که چارچوبهای مرجع نسبت به یکدیگر با سرعت یکنواختی حرکت می کنند. انیشتین نسبیت عام را معرفی نمود و اصل نسبیت را در حالت کلی تری به کارگرفت تا برای هر چارچوبی که قادر به تغییر مختصات عمومی است، صادق باشد. این نظریه تاثیرات گرانشی را هم در نظر می گیرد.این واژه امروزه کاربرد کلی تری پیدا کرده و برای ارجاع به هر موردی که در آن گرانش ناچیز است استفاده می شود. نسبیت عام تعمیمی بر نسبیت خاص است که گرانش را نادیده نمی گیرد. در نسبیت عام گرانش توسط هندسه نااقلیدسی توصیف می شود؛ به گونه ای که تاثیرات گرانشی با خمش فضازمان نمایش داده می شوند. نسبیت خاص تنهابه فضاهای تخت محدود است. همانگونه که خمش زمین در زندگی روزمره ناچیز به نظر می رسد خمش فضازمان نیز در مقیاسهای کوچک قابل صرف نظر کردن است و بنا بر این به صورت محلی نسبیت خاص تقریب قابل قبولی از نسبیت عام است. چارچوب های مرجع، مختصات ها و تبدیلات لورنتس ترسیمی از یک مخروط نوری نوشتار اصلی: تبدیلات لورنتسنسبیت بر پایه مفهوم "چارچوب های مرجع" استوار است. در اینجا منظور از واژه چارچوب مرجع، یک ژرفانمایی(پرسپکتیو) مشاهده ای در فضاست که تغییری در حرکت آن رخ نمی دهد(شتاب ندارد) که از طریق آن می توان یک موقعیت را در امتداد سه محور فضایی اندازه گرفت. افزون براین یک چارچوب مرجع توانایی تعیین زمان رویدادها از طریق یک 'ساعت'(هر دستگاه مرجعی با تناوب یکنواخت) را دارد.یک رویداد اتفاقی است که می توان یک زمان یکتا و مکانی در فضا نسبت به یک چارچوب مرجع نسبت داد: "نقطه" ای در فضازمان . از آنجاییکه سرعت نور در نسبیت در همه چارچوبهای مرجع ثابت است، می توان از پالس های نور برای اندازه گیری مطمئن فاصله ها و ارجاع به زمانهای ...
تبدیلات گالیله
تبدیلات گالیله <?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" /> دید کلی در برسی حرکت هر ذره باید یک چارچوب مرجع تعین کنیم که این چارچوببه عنوان ناظر در فیزیک تعبیر میشود. بعد از تعیین چارچوب مرجع به راحتی میتوانیمحرکت را مورد برسی قرار دهیم. البته لازم به ذکر است که در مورد هر حرکت ، چارچوبخاصی متناسب با نوع حرکت باید بکار ببریم. این مسئله نه تنها در مورد حرکت بلکه درمورد تمام رویدادها و پدیدههای فیزیکی مطرح است.به عنوان مثال برای اینکهبتوانیم در الکترو مغناطیس مقدار نیروی وارد بر یک جسم باردار را محاسبه کنیم،ابتدا باید یک چارچوب متناسب با سیستم تعریف کرده ، سپس پدیده را مورد برسی قراردهیم. حال سوال این است که اگر این چارچوب مرجع تغییر بکند (به عنوان مثال اگرچارچوب مرجع منتقل شود) ، در این صورت چه تغییری در برسی حاصل خواهد شد. این مسئلهبوسیله قواعد تبدیل بیان میشود. تعریف معادلاتی که در فیزیک کلاسیکمختصات فضا و زمان دو دستگاه مختصات را ، که با سرعت ثابت نسبت به یکدیگر حرکتمیکنند به هم مربوط میسازند، تبدیلات گالیله یا نیوتنی نامیده میشوند. هر ناظربا مشخص کردن مکان و زمان یک پدیده فیزیکی ، مانند یک بمب کوچک ، هر رویدادی رامیتواند توصیف کند. اگر مختصات فضایی و زمانی یک رویداد ، از نظر ناظر S1 بصورت:(t1 x1 y1 z1)و از نظر ناظر S2 بصورت:(t2 x2 y2 z2)باشد، و ناظر دوم نسبت به ناظر اولی باسرعت یکنواخت v حرکت بکند، در این صورت تبدیلات گالیله به شرح زیر خواهدبود:تبدیلات گالیله x2 = x1 - vt1 y2 = y1 z2 = z1 t2 = t1 لازم به ذکر است که تبدیلات سرعت و شتابنیز با مشتق گیری از روابط فوق حاصل میشود. هموردایی مکانیک کلاسیک درتبدیلات گالیله در فیزیک به عنوان یک اصل پذیرفته میشود که ، قوانین فیزیک درتمام دستگاههای لخت یکسان ، یا هموردا ، هستند. یعنی شکل ریاضی یک قانون فیزیکییکسان باقی میماند. به عبارت دیگر میتوان گفت که باید قوانین فیزیک تحت تبدیلاتگالیله یکسان باقی بمانند. از جمله قوانین فیزیکی که تحت این تبدیلات فرم ریاضی خودرا حذف میکنند، قوانین بقای اندازه حرکت خطی و قانون بقای انرژی است. همچنین قانوندوم نیوتن نیز که قانون بقای اندازه حرکت خطی از آن نتیجه میشود، فرم ریاضی خود راحفظ میکند.به عبارت دیگر میتوان گفت که تبدیلات گالیله و مکانیک کلاسیکمستلزم آن هستند که سه کمیت اساسی در آزمایشهای فیزیکی ، یعنی طول ، زمان و جرمهمگی از حرکت نسبی هر ناظری مستقل باشد. البته فیزیک نسبیت انیشتن در این عقیدهتجدید نظر میکند. و بجای طول ، زمان ، جرم و انرژی، دو قانون بقای جدید بوجودمیآورد. یعنی طول و زمان را باهم ادغام کرده ...
Symmetry & similarity
تقارن (symmetry) برای یک سیستم فیزیکی به این معناست که برخی از خواص فیزیکی و یا ریاضیاتی سیستم تحت برخی از تبدیلات، بی تغییر بماند. تبدیلات ممکن است پیوسته و یا گسسته باشند. تبدیلات پیوسته و گسسته هر کدام منجر به یک نوع از تقارن می شوند. تقارن های پیوسته توسط گروه های لی(Lie group) و تقارن های گسسته توسط گروههای متقارن توصیف می شوند. یک مثال مهم از تقارن، ناوردایی شکل قوانین فیزیک تحت تبدیلات مختصات است. ناوردایی به صورت ریاضی توسط یک تبدیل مشخص می شود که در آن برخی از کمیات بدون تغییر از مختصات باقی می مانند. برای مثال، دما درون یک اتاق ممکن است که ثابت باشد. به این دلیل که دما مستقل از موقعیت درون اتاق است،دما تحت تغییر موقعیت اندازه گیری، ناوردا باقی خواهد ماند. به طور مشابه، کره یکنواختی که حول مرکزش چرخانده شود، دقیقا همان چیزی به نظر می آید که قبل از چرخاندن بود و گفته می شود که کره دارای تقارن کروی است. تقارن های پیوسته: آنها به صورت ریاضی توسط توابع continuous یا smooth توصیف می شوند. یک زیر شاخه مهم در تقارن های پیوسته در فیزیک، تقارن های فضا- زمان است.تقارن های پیوسته فضا- زمان تقارن هایی هستند که شامل تبدیلات فضایی و یا زمانی و یا هر دو هستند. تقارن های فضایی( spatial symmetry ) آنهایی که هستند که فقط شامل هندسه فضایی سیستم فیزیکی میشوند و تقارن های زمانی (temporal symmetry)فقط شامل تبدیلات زمانی هستند و تقارن های spatio-temporal شامل هر دو تغییر هستند. تبدیل زمان: یک سیستم فیزیکی ممکن است خواصی یکسانی بر روی یک بازه دلتای t داشته باشد، به صورت ریاضی این به عنوان یک ناوردایی تحت تبدیل t-t+a برای هر مقدار حقیقی t، بیان می شود. برای مثال در فیزیک کلاسیک، ذره ای را فرض کنید که در ارتفاع H از سطح زمین قرار گرفته است و انرژی پتانسیل mgh دارد. اگر ارتفاع ذره تغییر نکند، انرژی پتانسیل گرانشی ذره در تمام لحظات یکسان خواهد بود.به عبارت دیگر، با این فرض که حالت ذره در زمان t و t+3 تغییر نکند، انرژی پتانسیل گرانشی تحت تبدیل t به t+3 ناوردا باقی می ماند. تبدیل فضایی: این نوع از تقارن ها با تبدیلات r به r+a بیان می شوند و توصیف کننده موقعیت هایی هستند که تحت تبدیل آنها یک یا چند ویژگی سیستم تغییر نخواهدکرد. برای مثال، دمای اتاق ممکن است مستقل از جایی که شما آن را اندازه می گیرید باشد. چرخش فضایی: این نوع از تقارن های فضایی، در دسته proper rotation و improper rotation طبقه بندی می شوند. اخیرا آنها فقط ordinary rotation هستند که به صورت ریاضی با ماتریس های مربعی با دترمینان یک توصیف می شوند ولی قبلا آنها با ماتریس های مربعی با دترمینان 1- هم نشان داده می شدند که شامل proper rotation ...
