برنامه ریزی خطی
برنامه ریزی خطی
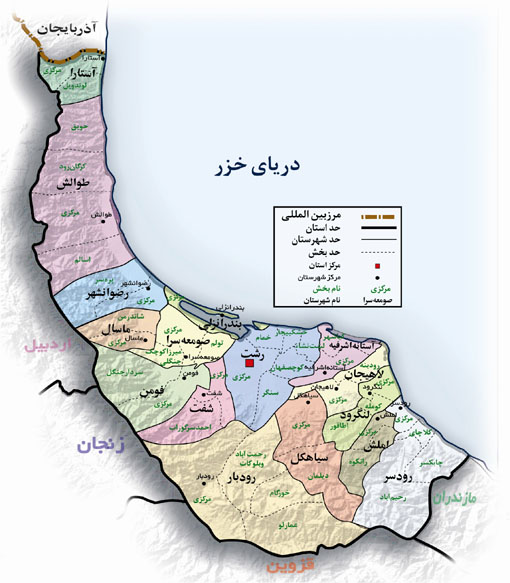
کاربرد برنامه ریزی خطی در فعالیت های کشاورزی روستاهای گیلان سهراب کرد رستمی 1مسعود گلدوست آذری 2 چكيده : چهلوشش درصد جمعیت استان گیلان در مناطق روستای زندگی می کنند که این آمار در بعضی از شهرستانهای استان گیلان همچون شفت، تالش و فومن به مرز 86 ، 72 و 70 درصد نیز می رسد، ولی با درنظر گرفتن نرخ بالای بیکاری در استان گیلان، مخصوصاً در مناطق روستایی که از مزیت های نسبی فراوانی نیز برخوردار هستند به نظرمی رسد که برای غلبه بروضعیت موجود ترویج فعالیت هایکارآفرینانه، این امکان را به وجود خواهد آورد که هر چه سریعتر جوامعروستایی در استان گیلان به توسعه و پیشرفت اقتصادی دست یابد. ولی كمبود درآمد عامل مهمي است كه اگر براي آن چارهاي انديشيده نشود اجازه نميدهد طرحهاي توسعه روستايي به ثمر بنشيند و روستاها توسعه يافته و از حركت ساکنان آن به سمت شهرهاي بزرگ کاسته شود . كمبود درآمد روستاييان ناشي از چندين مساله است: 1 - افزايش جمعيت روستاييان (مقدار مطلق) 2 - بيكاري (كامل يا فصلي) 3 - بهرهوري پايين افراد و منابع 4 - عدمجذابيت براي سرمايهگذاري 5 - ضعف فضاي كسب وكار 6 - محدودیت منابع و کوچک شدن قطعات زمینهای زراعی متعلق به یک فرد ، به همین علت بسیاری از کشاورزان در روستاهای گیلان وادار شدهاند که در راستای دستیابی به سطح درآمدی بالاتر با قطعیت زیاد، در کنار کشت زراعی خود به دنبال فعالیت های دیگری باشند . اقدامات دولت، از طریق اعطای تسهیلات اعتباری و غیره باعث گردیده که حوزه های مختلفی برای افراد خانواده در زمینه های مختلف از جمله کسب و کار خانگی[1] ، کسب و کارهای خانوادگی[2] و کسب و کار روستایی[3] به وجود آید،که محوریترین فعالیتها در روستا توجه به اشتغال در بخش کشاورزی است . اما کشاورزان گیلانی به دلیل منابع محدود در استفاده از پتانسلهای بخش کشاورزی در زیرشاخههای متعدد آن با در نظر گرفتن امکاناتی که دارند، با تصمیمگیری بهینه تخصیص منابع مواجهند . لذا توسعه و گسترش استفاده از برنامه ریزی خطی به طور عام و استفاده از مدل برنامهریزی خطی چند بخشی به طور خاص این امکان را برای روستائیان استان گیلان به وجود می آورد که بخشهای مختلف و نسبتاً مستقل یک واحد زراعی را مورد بحث و توجه قرار دهند، در این وضعیتی امکان تخصیص مشترک منابع تولیدی محدود کننده بین فعالیت های مختلف کشاورزی به صورت هم زمان مطرح میشود ، که با طراحی انواع برنامه ریزی های خطی در داخل واحد تولیدی و در بین کشاورزان منطقه، به جهت نوآوری در ارائه روشی جدید در فرآیند تولید،یافتن منابع جدید و به وجود آمدن یک تشکیلات منسجم تداعی کننده نظریات ...
برنامه ريزي خطي (Lp)
برنامه ريزي خطي ... Lp<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" /> تعاریف برنامه ریزی خطیزهرا صابري،زهرا کاشفي 1- مقدمهدر رياضيات، مسائل برنامه ريزي خطي شامل بهينه سازي تابع هدفي خطي است که بايستي يکسري محدوديت در فرم هاي تساوي هاي خطي و نامساوي برقرار شوند. به طور خيلي غيررسمي برنامه ريزي خطي استفاده از مدل رياضي خطي براي بدست آوردن بهترين خروجي(به طور مثال حداکثر سود، حداقل کار) با توجه به شرط هاي داده شده (براي مثال فقط 30 ساعت کار در هفته، کار غير قانوني انجام ندادن و غيره) است. و به طور رسمي تر در يک چند سقفي (مانند چندضلعي يا چندوجهي) که تابعي با مقدار حقيقي بر روي آن تعريف شده است، هدف يافتن نقطه اي در اين چند سقفي است که تابع هدف بيشترين يا کمترين مقدار را دارا باشد. اين نقاط ممکن است موجود نباشد، اما اگر وجود داشته باشند جست و جو در ميان رئوس چند ضلعي يافتن حداقل يکي از آن ها را تضمين مي کند.برنامه ريزي خطي به صورت استاندارد مي توانند نمايش داده شوند:Maximize cTx Subject to Ax ≤ bx ≥ 0 X بيانگر بردار متغير ها مي باشد و همچنين c وb بردار ضرايب و A ماتريس ضرايب. عبارتي که بايد حداکثر يا حداقل شود تابع هدف نام دارد (در اين مورد cTx ).عبارت b Ax ≤ شرايطي هستند که يک چند وجهي محدب را نمايش مي دهند که تابع هدف روي آن بايد بهينه شود. برنامه ريزي خطي مي تواند در زمينه هاي مختلف مطالعه مورد استفاده قرار گيرد. برنامه ريزي خطي به طور عمده در موقعيت هاي تجاري و اقتصادي مورد استفاده قرار مي گيرد اما براي بعضي از مسائل مهندسي نيز مي تواند به کار برده شود. بعضي از صنعت ها که برنامه ريزي خطي را مورد استفاده قرار مي دهند عبارتند از حمل و نقل، انرژي، مخابرات و کارخانه ها و … . همچنين در مدل کردن مسائلي از قبيل برنامه ريزي، مسير يابي، زمانبندي، تخصيص و طراحي مفيد است.يک ارزيابي انجام شده از 500 شرکت بزرگ دنيا، نشان داد که 85% درصد آنها از برنامه ريزي خطي استفاده نموده اند.[1] 2-تاريخچه برنامه ريزي خطيمسئله حل يک سيستم نامساوي خطي به زمان فوريه[1] بر مي گردد. برنامه ريزي خطي به عنوان يک مدل رياضي به وجود آمد و در زمان جنگ جهاني دوم و پس از آن معلوم شد که طرح ريزي و هم آهنگي پروژه هاي مختلف و استفاده موثر از منابع کمياب يک ضرورت است. تيم SCOOP (محاسبات علمي برنامه هاي بهينه) نيروي هوايي ايالات متحده کار جدي خود را در ژوئن 1947 شروع کرد. ماحصل آن، ابداع روش سيمپلکس توسط جورج.بي.دانتزيک[2] در پايان تابستان 1947 بود. برنامه ريزي خطي به سرعت مورد توجه اقتصاد دانان، رياضي دانان، آماردانان، و موسسات دولتي قرار گرفت. در تابستان 1949 کنفرانسي ...
مطالب نشریه اقتصاد کشاورزی 4
برنامه ریزی خطی ۱- مقدمه در ریاضیات، مسائل برنامه ریزی خطی شامل بهینه سازی تابع هدفی خطی است که بایستی یکسری محدودیت در فرم های تساوی های خطی و نامساوی برقرار شوند. به طور خیلی غیررسمی برنامه ریزی خطی استفاده از مدل ریاضی خطی برای بدست آوردن بهترین خروجی(به طور مثال حداکثر سود، حداقل کار) با توجه به شرط های داده شده (برای مثال فقط ۳۰ ساعت کار در هفته، کار غیر قانونی انجام ندادن و غیره) است. و به طور رسمی تر در یک چند سقفی (مانند چندضلعی یا چندوجهی) که تابعی با مقدار حقیقی بر روی آن تعریف شده است، هدف یافتن نقطه ای در این چند سقفی است که تابع هدف بیشترین یا کمترین مقدار را دارا باشد. این نقاط ممکن است موجود نباشد، اما اگر وجود داشته باشند جست و جو در میان رئوس چند ضلعی یافتن حداقل یکی از آن ها را تضمین می کند. برنامه ریزی خطی به صورت استاندارد می توانند نمایش داده شوند: Maximize cTx Subject to Ax ≤ b x ≥ ۰ X بیانگر بردار متغیر ها می باشد و همچنین c وb بردار ضرایب و A ماتریس ضرایب. عبارتی که باید حداکثر یا حداقل شود تابع هدف نام دارد (در این مورد cTx ).عبارت b Ax ≤ شرایطی هستند که یک چند وجهی محدب را نمایش می دهند که تابع هدف روی آن باید بهینه شود. برنامه ریزی خطی می تواند در زمینه های مختلف مطالعه مورد استفاده قرار گیرد. برنامه ریزی خطی به طور عمده در موقعیت های تجاری و اقتصادی مورد استفاده قرار می گیرد اما برای بعضی از مسائل مهندسی نیز می تواند به کار برده شود. بعضی از صنعت ها که برنامه ریزی خطی را مورد استفاده قرار می دهند عبارتند از حمل و نقل، انرژی، مخابرات و کارخانه ها و … . همچنین در مدل کردن مسائلی از قبیل برنامه ریزی، مسیر یابی، زمانبندی، تخصیص و طراحی مفید است.یک ارزیابی انجام شده از ۵۰۰ شرکت بزرگ دنیا، نشان داد که ۸۵% درصد آنها از برنامه ریزی خطی استفاده نموده اند.[۱] ۲-تاریخچه برنامه ریزی خطی مسئله حل یک سیستم نامساوی خطی به زمان فوریه[۱] بر می گردد. برنامه ریزی خطی به عنوان یک مدل ریاضی به وجود آمد و در زمان جنگ جهانی دوم و پس از آن معلوم شد که طرح ریزی و هم آهنگی پروژه های مختلف و استفاده موثر از منابع کمیاب یک ضرورت است. تیم SCOOP (محاسبات علمی برنامه های بهینه) نیروی هوایی ایالات متحده کار جدی خود را در ژوئن ۱۹۴۷ شروع کرد. ماحصل آن، ابداع روش سیمپلکس توسط جورج.بی.دانتزیک[۲] در پایان تابستان ۱۹۴۷ بود. برنامه ریزی خطی به سرعت مورد توجه اقتصاد دانان، ریاضی دانان، آماردانان، و موسسات دولتی قرار گرفت. در تابستان ۱۹۴۹ کنفرانسی در برنامه ریزی و برای برنامه ریزی مخارج و برگشت ها توسعه داده شد به طوری که با مسئولیت کمیته Cowles ...
برنامه ریزی خطی

برنامه ریزی خطی تألیف مختار اس. بازارا، جان جی. جارویس، حنیف دی. شرالی ترجمه اسماعیل خرمانتشارات نشر کتاب دانشگاهی این کتاب به عنوان مرجع اصلی درس تحقیق در عملیات پیشرفته برای رشته های ریاضیات و کاربردها، مدیریت، مهندسی مالی و... در دانشگاههای دولتی و غیر دولتی در نظر گرفته شده است.فهرست مطالب فصل اول: مقدمهمسأله برنامه ریزی خطیمدل بندی مثالهای برنامه ریزی خطیحل هندسیفضای احتیاجنمادهافصل دوم: جبر خطی، آنالیز محدب و مجموعههای چندوجهیبردارهاماتریسهامعادلات خطی هم زمانمجموعههای محدب و توابع محدبمجموعههای چندوجهی و مخروطهای چندوجهیدیدگاه مهندسینمایش مجموعههای چندوجهیفصل سوم: روش سیمپلکسنقاط رأس و بهینگیجوابهای شدنی پایهکلید روش سیمپلکسسبب هندسی روش سیمپلکسجبر روش سیمپلکسروش سیمپلکسروش سیمپلکس در جدولمحورگیری چندگانهفصل چهارم: شروع حل و هم گراییجوابهای شدنی پایه آغازینروش دو فازیروش M- بزرگمقایسه روشهای دو فازی و M- بزرگروش تک متغیر مصنوعینباهیدگی، دوری و ایستاعتبار دو قاعده ممانعت از دوریفصل پنجم: عملکردهای ویژه سیمپلکس و شرایط بهینگیروش سیمپلکس اصلاح شدهروش سیمپلکس متغیرهای کران دارلم فارکاس از طریق روش سیمپلکسفصل ششم: دوگان و تحلیل حساسیتفرمول بندی مسأله دوگانروابط اولیه – دوگانتغییر اقتصادی دوگانروش سیمپلکس دوگانروش اولیه – دوگانروش محدودیت مصنوعیتحلیل حساسیتتحلیل پارامتری
دانلود کتاب برنامه ریزی خطی(بازارا)
برنامه ریزی خطی نویسنده: مختار اس. بازارا - جان جی. جارویس-حنیف دی. شرالی Linear Programming and Network Flows Mokhtar S. Bazaraa John J. Jarvis Hanif D. Sheraliپسورد : safaei دانلوددانلود(لینک کمکی)
برنامه ریزی خطی
مفروضات برنامه ریزی خطیفرض جمع پذیری :روابط به صورت جمع بیان می شود*فرض تناسب : هر فعالیت به تنهایی و مستقل از سایر فعالیتها عمل میکند * **فرض بخش پذیری : متغیرهای تصمیم میتوانند غیر صحیح نیز باشندفرض معین بودن: کلیه پارامتر ها مقادیر ثابتی هستند*در ادامه ی مطالب روش ترسیمی و سیمپلکس همراه با اسلاید ها را ارائه خواهم داد**در صورت نادیده گرفتن این فرض برنامه ریزی عدد صحیح را خواهیم داشت
برنامه ریزی اعداد صحیح چیست ؟
برنامه ریزی عدد صحیحاز جمله مسائل تحقیق در عملیات، مسائلی هستند که در آنها برخی یا همه متغیرها عدد صحیح باشند. این متغیرهای صحیح می توانند فقط صفرویک باشند و یا سایر متغیرهای صحیح. این مدلها کاربردهای زیادی در مسائل واقعی دارند زیرا بسیاری از متغیرها در دنیای واقعی به صورت اعداد صحیح هستند. برای حل این مدلها روشهای خاصی وجود دارد که در این مقاله به آنها اشاره شده است.برنامهریزی متغیرهای عدد صحیح نوع خاصی از برنامهریزی خطی است که در آن یک یا چند متغیر باید عدد صحیح باشند. در بسیاری از مسایل واقعی مقادیر اعشاری قابل قبول نیستند.مثلا اگر متغیر های مسئله، تعداد نیروی استخدام باشد، عددی مانند 3.5 برای آن معنا نخواهد داشت.بنابراین در بسیاری از مسائل واقعی متغیرها به صورت عدد صحیح هستند.برای حل چنین مسائلی روشهای خاصی اراده شده است که در این مقاله به طور خلاصه به آنها خواهیم پرداخت.تشریح موضوع:دربرنامه ريزي عدد صحيح، تابع هدف خطي، محدوديتها خطي و برخی از متغيرها صحیح می باشند.انواع مدل برنامه ريزي عدد صحيح عبارتند از:1- برنامه ريزي عدد صحيح محض: در این مدل، تمام متغیرها عدد صحیح هستند.2- برنامه ريزي عدد صحيح مختلط:در این مدل برخی از متغیرها صحیح و برخی دیگر عدد حقیقی هستند.3- برنامه ريزي عدد صحيح صفر و يك: در این مدل تمام متغیرها عدد صحیح صفر و یک هستند.مدل سازی عدد صحیح دارای قابلیت انعطاف بیشتری بوده ودرعین حال حل چنین مشکلاتی در عمل مشکل تر می باشد. به عبارت دیگر حل یک مدل برنامه ریزی خطی با میلیونها متغیر، از نقطه نظر حل ممکن است بسیار ساده باشد،اما غالبا حل مدلهای برنامه ریزی با متغیرهای صحیح که دارای صدها متغیر هستند بسیار مشکل است. از آنجای که بیشتر مدل های برنامه ریزی عدد صحیح، شکل برنامه ریزی خطی دارند، لذا از تمام ابزارهای موجود دراین زمینه می توان بهرمند شد، به علاوه استفاده ازمتغیرهای صحیح، به مدل ساز تواناییهای فراوانی می دهد که درنتیجه آن می تواند مسایل بسیاری را در عمل فرموله کند. برنامه ریزی عدد صحیح اجازه اعمال منطق هایی که در مدل سازی برنامه ریزی خطی میسر نیست به ما می دهد. روش حل مسائل فرموله شده در قالب برنامه ریزی اعداد صحیح، به دو دسته برشی و تجسسی تقسیم می شوند.روشهای برشی در ابتدا با حل مسئله برنامه ریزی خطی در حالت متغیر پیوسته شروع می شوند.سپس با اضافه کردن محدودیت های اضافی ، هربار شرایط لازمی جهت منفصل شدن جواب به وجود می آید. تا اینکه به مرور حل غایی در حالت پیوسته ، شرط انفصال جواب را ارضا نماید.این روش را از آن جهت برشی نامند که محدودیت اضافی، قسمتی از فضای جواب را برش داده ...
