اندازه ی زوایای مثلثاتی
در این مقاله روشی برای محاسبه ی سینوس زوایای دلخواه ارائه می شود كه به كمك آن
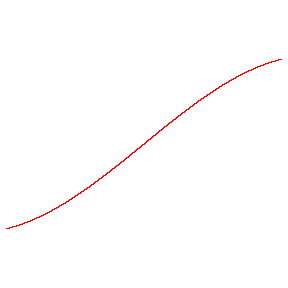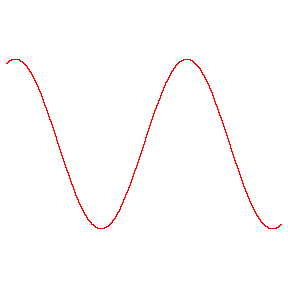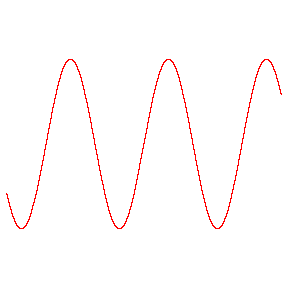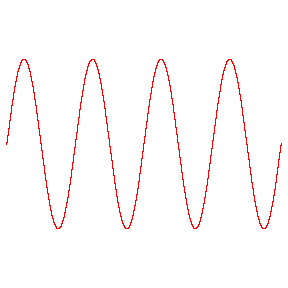
در این مقاله روشی برای محاسبه ی سینوس زوایای دلخواه ارائه می شود كه به كمك آن می توان سایر نسبت های مثلثاتی را نیز به دست آورد . سینوس یك زاویه حاده چیست؟در مثلث قائم الزاویه سینوس زاویه حاده برابر است با:نسبت ضلع رو به رو به این زاویه،بر وتر.یك روش محاسبه برای زاویه های خیلی كوچك این است كه نسبت قوس را به شعاع حساب كنیم.مثلا" برای زاویه 1 درجه داریم:(شكل 1) كه قوس است.و در آن ...14159/3= است.و AB=R . پس : .و به همین ترتیب می توان به دست آورد: حال اگر سینوس 30 درجه را با روش فوق محاسبه كنیم ، عدد 524/0 را به جای 500/0 به دست می آوریم كه خطای حاصل یعنی قریب 5% خواهد بود و این بیش از اندازه زیاد است. برای این كه بتوانیم مرزی برای روش فوق پیدا كنیم سینوس زاویه 15درجه را با دقت محاسبه می كنیم:بقیه در ادامه مطلب...در این مقاله روشی برای محاسبه ی سینوس زوایای دلخواه ارائه می شود كه به كمك آن می توان سایر نسبت های مثلثاتی را نیز به دست آورد . سینوس یك زاویه حاده چیست؟در مثلث قائم الزاویه سینوس زاویه حاده برابر است با:نسبت ضلع رو به رو به این زاویه،بر وتر.یك روش محاسبه برای زاویه های خیلی كوچك این است كه نسبت قوس را به شعاع حساب كنیم.مثلا" برای زاویه 1 درجه داریم:(شكل 1) كه قوس است.و در آن ...14159/3= است.و AB=R . پس : .و به همین ترتیب می توان به دست آورد: حال اگر سینوس 30 درجه را با روش فوق محاسبه كنیم ، عدد 524/0 را به جای 500/0 به دست می آوریم كه خطای حاصل یعنی قریب 5% خواهد بود و این بیش از اندازه زیاد است. برای این كه بتوانیم مرزی برای روش فوق پیدا كنیم سینوس زاویه 15درجه را با دقت محاسبه می كنیم:با توجه به شكل 2 داریم: شكل2 BC را به اندازه ی خودش تا نقطه ی D امتداد می دهیم و سپس D را به A وصل می كنیم. در این صورت دو مثلث مساوی ADC و ABC و زاویه BAD مساوی 30درجه به دست می آید. عمود BE را بر AD فرود می آوریم ؛ مثلث قائم الزاویه BAE بازاویه 30 درجه(زاویه BAE ) به دست می آیدو بنابراین =BE می شود.حال AE را از مثلث ABE طبق رابطه ی فیثاغورث به دست می آوریم: حال در مثلث BED طول BD را محاسبه می كنیم: اگر به سه رقم اعشار اكتفا كرده باشیم ، این عدد، همان عددی است كه در جدول ها برای 15 Sin ضبط شده است. حالا اگر مقدار را با روش نسبت قوس بر شعاع محاسبه كنیم به عدد 262 /0 می رسیم:با مقایسه دو عدد 262/0و259/0 می بینیم كه اگر هر دو را تا دو رقم اعشار گرد كنیم به عدد 26/0 می رسیم . خطای حاصل از تبدیل مقدار دقیق تر 259/0 به 26/0 مساوی ،یعنی قریب4/0% است. كه این مقدار خطا برای محاسبه های عادی مانعی ندارد. برای زاویه های بین 15 درجه و 30 درجه می توانیم از تناسب استفاده كنیم .به این ترتیب استدلال می ...
توابع مثلثاتی معکوس
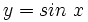
منشا توابع مثلثاتی معکوس، مسائلی است که در آن ها باید با استفاده از اندازه ی اضلاع یک مثلث، زوایای آن را به دست آورد. این توابع، پاد مشتق بسیاری از توابع دیگر هم هستند و لذا در جواب های تعدادی از معادلات دیفرانسیل مورد بحث در ریاضیات، مهندسی و فیزیک ظاهر میشوند. آرک سینوس تابع یک به یک نیست؛ این تابع در بازه های به طول ، دو بار سراسر برد مقادیرش، یعنی از تا را طی می کند. ولی اگر دامنه ی سینوس را به بازه ی محدود کنیم، آن گاه تابع محدود شده ی یک به یک و بنابر این دارای معکوسی است که با نمایش داده می شود و غالبا به صورت نوشته می شود. با توجه به شکل1، اگر ، آن گاه آرکی (قوسی) از دایره ی واحد است که سینوسش می باشد. پس به ازای هر مقدار در بازه ی ، عددی از بازه ی است که سینوس آن خواهد بود. توجه:نمودار آرک سینوس نسبت به مبدا متقارن است زیرا که نمودار نسبت به مبدا متقارن می باشد. از نظر جبری، این بدین معناست که به ازای هر در دامنه ی آرک سینوس: که راه دیگری است برای بیان فرد بودن تابع . آرک کسینوس تابع کسینوسی هم نظیر تابع سینوسی یک به یک نیست، اما اگر به بازه ی محدود شود یک به یک خواهد بود و معکوسی دارد که به آرک کسینوس معروف است. به ازای هر مقدار در بازه ی ، عددی از بازه ی می باشد که کسینوس آن است. همان طور که در شکل2 ملاحظه می کنید، آرک کسینوس در اتحاد یا صدق می کند و با توجه به مثلث شکل3 نیز دیده می شود که به ازای : زیرا در این صورت و زوایای متمم در یک مثلث قایم الزاویه اند که طول وترش یک واحد و طول یکی از ساق هایش واحد است. نکته: به سادگی ثابت می شود که اتحاد به ازای سایر مقادیر واقع در هم برقرار است. معکوس چهار تابع مثلثاتی اساسی دیگر ، ، و هم، وقتی به طور مناسبی محدود شوند، معکوس دارند. معکوس یا نمایش داده می شود . دامنه ی آرک تانژانت تمام اعداد حقیقی است و بردش، بازه ی باز است. به ازای هر مقدار ، زاویه ای است بین و و تانژانت آن است. نمودار نسبت به مبدا متقارن است زیرا شاخه ای است از نمودار که نسبت به مبدا متقارن است. از نظر جبری، این بدین معناست که:. آرک تانژانت هم نظیر آرک سینوس تابع فردی از است. معکوس های توابع (محدود شده): چنان انتخاب شده اند که در روابط زیر صدق کنند:
مثلث
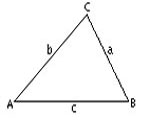
مثلث ار اساسی ترین اشکال در هندسه میباشد.یک مثلث دارای سه راس است که سه ضلع این رئوس را به هم وصل میکند.در هندسه اقلیدسی این اضلاع خطوطی مستقیم هستند. ولی در هندسه کروی این اضلاع کمان هایی از دایره عظیمه میباشند.این دو نوع مثلث را میتوانید در شکلهای روبرو مشاهده نمایید. انواع مثلث مثلث متساوی الاضلاع: مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای داخلی این مثلث نیز با هم برابرند. مثلث متساوی الساقین: مثلثی است که دارای دو ضلع با طولهای مساوی استو دو زاویه داخلی برابر دارد. البته مثلث میتواند دارای سه ضلع با طولهای مختلف و زوایای غیر مساوی باشد. مثلث قائم الزاویه: مثلثی را گویند که یکی از زوایای آن 90درجه باشد.نسبت های مثلثاتی مانند sin و cos ،بر روی مثلث قائم الزاویه تعریف میشوند. مثلث منفرجه: مثلثی را گویند که یکی از زوایای داخلی آن بیشتر از 90 درجه باشد. مثلث حاده : مثلثی را گویند که تمام زوایای داخلی آن کمتر از 90 درجه باشد. 300 سال قبل از میلاد اقلیدس ،اصول اولیه درباره مثلث را ارائه داد.به عنوان مثال یکی از اصول مهم در مورد مثلث این است که مجموع زوایای داخلی یک مثلث برابر 180 درجه است. بر اساس این اصل میتوان با معلوم بودن دو زاویه از مثلث اندازه زاویه سوم را بدست آورد. یکی از مهمترین قضایای موجود در مثلثات قضیه فیثاغورث میباشد.در این قضیه رابطه بین وتر و اضلاع قائم یک مثلث قائم الزاویه بیان میشود. محاسبه مساحت مثلث برای محاسبه مساحت یک مثلث روشهای مختلفی وجود داردو در ادامه به توضیح این روشها میپردازیم روش هندسی برای محاسبه مساحت یک مثلث باید طول ارتفاع مثلث و نیز طول قاعده(ضلعی که ارتفاع بر آن عمود است) آن را داشته باشیم.آنگاه میتوانیم از فرمول زیر استفاده کنیم: در این فرمول b طول قاعده و h طول ارتفاع مثلث میباشد. در شکل زیر نحوه بدست آمدن این فرمول بیان شده است: تبدیل مثلث به یک متوازی الاضلاع که دو برابر مثلث مساحت دارد وسپس تبدیل متوازی الضلاع به یک مستطیل برای پیدا کردن مساحت مثلث (قسمت سبز) ابتدا یک کپی از مثلث (قسمت آبی) را برداشته و آن را 180 درجه میچرخانیم و به مثلث اولیه متصل میکنیم تا یک متوازی الاضلاع بدست آید. با بریدن قسمتی از متوازی الاضلاع و متصل کردن آن به ضلع دیگر آن(همانند شکل) یک مستطیل ایجاد میشود. چون مساحت مستطیل برابر bh است .پس مساحت مثلث اولیه، نصف این مساحت خواهد بود. روش برداری محاسبه مساحت متوازی الاضلاع با استفادهاز ضرب خارجی دو بردار مساحت یک متوازی الاضلاع را میتوان با استفاده از بردارها محاسبه کرد.اگر AB,AC را مطابق شکل فرض کنیم آنگاه مساحت ABCD برابر |AB × AC| خواهد ...
مثلث
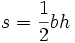
مثلث ار اساسی ترین اشکال در هندسه میباشد.یک مثلث دارای سه راس است که سه ضلع این رئوس را به هم وصل میکند.در هندسه اقلیدسی این اضلاع خطوطی مستقیم هستند. ولی در هندسه کروی این اضلاع کمان هایی از دایره عظیمه میباشند.این دو نوع مثلث را میتوانید در شکلهای روبرو مشاهده نمایید. انواع مثلث مثلث متساوی الاضلاع: مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای داخلی این مثلث نیز با هم برابرند. مثلث متساوی الساقین: مثلثی است که دارای دو ضلع با طولهای مساوی است و دو زاویه داخلی برابر دارد. البته مثلث میتواند دارای سه ضلع با طولهای مختلف و زوایای غیر مساوی باشد. مثلث قائم الزاویه: مثلثی را گویند که یکی از زوایای آن 90درجه باشد.نسبت های مثلثاتی مانند sin و cos ،بر روی مثلث قائم الزاویه تعریف میشوند. مثلث منفرجه: مثلثی را گویند که یکی از زوایای داخلی آن بیشتر از 90 درجه باشد. مثلث حاده : مثلثی را گویند که تمام زوایای داخلی آن کمتر از 90 درجه باشد. 300 سال قبل از میلاد اقلیدس ،اصول اولیه درباره مثلث را ارائه داد.به عنوان مثال یکی از اصول مهم در مورد مثلث این است که مجموع زوایای داخلی یک مثلث برابر 180 درجه است. بر اساس این اصل میتوان با معلوم بودن دو زاویه از مثلث اندازه زاویه سوم را بدست آورد. یکی از مهمترین قضایای موجود در مثلثات قضیه فیثاغورس میباشد.در این قضیه رابطه بین وتر و اضلاع قائم یک مثلث قائم الزاویه بیان میشود. محاسبه مساحت مثلث برای محاسبه مساحت یک مثلث روشهای مختلفی وجود داردو در ادامه به توضیح این روشها میپردازیم: روش هندسی برای محاسبه مساحت یک مثلث باید طول ارتفاع مثلث و نیز طول قاعده(ضلعی که ارتفاع بر آن عمود است) آن را داشته باشیم.آنگاه میتوانیم از فرمول زیر استفاده کنیم: در این فرمول b طول قاعده و h طول ارتفاع مثلث میباشد. در شکل زیر نحوه بدست آمدن این فرمول بیان شده است: تبدیل مثلث به یک متوازی الاضلاع که دو برابر مثلث مساحت دارد وسپس تبدیل متوازی الضلاع به یک مستطیل برای پیدا کردن مساحت مثلث (قسمت سبز) ابتدا یک کپی از مثلث (قسمت آبی) را برداشته و آن را 180 درجه میچرخانیم و به مثلث اولیه متصل میکنیم تا یک متوازی الاضلاع بدست آید. با بریدن قسمتی از متوازی الاضلاع و متصل کردن آن به ضلع دیگر آن(همانند شکل) یک مستطیل ایجاد میشود. چون مساحت مستطیل برابر bh است .پس مساحت مثلث اولیه، نصف این مساحت خواهد بود. روش برداری محاسبه مساحت متوازی الاضلاع با استفادهاز ضرب خارجی دو بردار مساحت یک متوازی الاضلاع را میتوان با استفاده از بردارها محاسبه کرد.اگر AB,AC را مطابق شکل فرض کنیم آنگاه مساحت ABCD برابر |AB × AC| ...
جدول مثلثاتی
سلام امروز مقدار زاویه های 0 تا 90 درجه برای سینوس ، کسینوس ، تانژانت ، سکانت و کسکانت رو برای دانلود گذاشتم. شاید به درد تمام بازدیدکنندگان نخوره اما کسایی که فیزیک میخونن مقدار این زاویه ها به دردشون میخوره مخصوصا کسایی که ماشین حساب معمولی دارن. دانلود فایل notepad فشرده شده دانلود فایل exel
زاویه و دایره
.:: زاویه و دایره ::. دایره: (circle) مجموعه نقاطی از صفحه که فاصله ی آن از یک نقطه به نام مرکز برابر باشند ، دایره نامیده می شود. دایره ی c به مرکز o و شعاع R را با نماد نشان می دهیم . وتر دایره :(circle chord) پاره خطی که دو نقطه از محیط دایره را به هم وصل می کند . هر دایره بیشمار وتر دارد . مانند وتر های AB و CD در دایره ی C . قطر دایره:(circle axis) بزرگترین وتر در هر دایره را قطر می نامند . قطر وتر ی از دایره است که از مرکز می گذرد مانند قطر MN در دایره ی C. کمان دایره :(circlearc) قسمتی از محیط دایره را می گویند که به دو نقطه روی محیط دایره محدود شده باشد. اگر دو نقطه ی A و B را روی دایره C در نظر بگیریم دو کمان پدید می آید ، کمان کوچکتر را به صورت و کمان بزرگتر را به صورت می خوانیم . í نقطه و دایره : نقطه و دایره نسبت به هم 3 وضعیت دارند :1 نقطه داخل دایره است. 2 نقطه روی دایره است. 3 نقطه خارج دایره است . íوضع یک خط و یک دایره نسبت به هم: خط و دایره نسبت به هم سه حالت دارند: 1. خط خارج دایره است که در این صورت فاصله ی خط تا مرکز دایره از شعاع بزرگتر است. یعنی d 2.خط بر دایره مماس است.که در این صورت فاصله ی خط تا مرکز دایره با شعاع مساوی است . یعنی d = r 3.خط دایره را در دو نقطه قطع می کند که در این صورت فاصله ی خط تا مرکز دایره از شعاع کو چکتر است. یعنی: d < r زاویه و دایره: زاویه ی مرکزی:زاویه ای که رأس آن مرکز دایره باشد زاویه ی مرکزی نامیده می شود. در شکل مقابل زاویه ی AOB یک زاویه مرکزی است و کمان AB کمان مقابل آن می باشد. نکته: اندازه ی زاویه ی مرکزی با کمان مقابلش مساوی است. زاویه ی محاطی: زاویه ی محاطی زاویه ای است که رأس آن روی دایره و اضلاع آن دو وتر از همان دایره باشند . در شکل مقابل زاویه ی یک زاویه ی محاطی است و کمان BC ، کمان مقابل آن می باشد. نکته :اندازه ی زاویه ی محاطی نصف کمان مقابل آن است. زاویه ی ظلّی : هر زاویه ای که رأسش روی دایره و یک ضلع آن وتری از دایره و ضلع دیگرش بر دایره مماس باشد ، زاویه ی ظّلی نامیده می شود. در شکل مقابل یک زاویه ی ظّلی و کمان AB کمان مقابل به زاویه ی ظّلی A ...
روش محاسبه سطح مثلث و اشکال هندسی
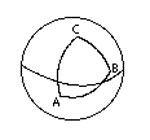
مثلث ار اساسی ترین اشکال در هندسه میباشد.یک مثلث دارای سه راس است که سه ضلع این رئوس را به هم وصل میکند.در هندسه اقلیدسی این اضلاع خطوطی مستقیم هستند. ولی در هندسه کروی این اضلاع کمان هایی از دایره عظیمه میباشند.این دو نوع مثلث را میتوانید در شکلهای روبرو مشاهده نمایید. انواع مثلثمثلث متساوی الاضلاع: مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای داخلی این مثلث نیز با هم برابرند.مثلث متساوی الساقین: مثلثی است که دارای دو ضلع با طولهای مساوی استو دو زاویه داخلی برابر دارد.البته مثلث میتواند دارای سه ضلع با طولهای مختلف و زوایای غیر مساوی باشد.مثلث قائم الزاویه: مثلثی را گویند که یکی از زوایای آن 90درجه باشد.نسبت های مثلثاتی مانند sin و cos ،بر روی مثلث قائم الزاویه تعریف میشوند.مثلث منفرجه: مثلثی را گویند که یکی از زوایای داخلی آن بیشتر از 90 درجه باشد.مثلث حاده : مثلثی را گویند که تمام زوایای داخلی آن کمتر از 90 درجه باشد.300 سال قبل از میلاد اقلیدس ،اصول اولیه درباره مثلث را ارائه داد.به عنوان مثال یکی از اصول مهم در مورد مثلث این است که مجموع زوایای داخلی یک مثلث برابر 180 درجه است. بر اساس این اصل میتوان با معلوم بودن دو زاویه از مثلث اندازه زاویه سوم را بدست آورد.یکی از مهمترین قضایای موجود در مثلثات قضیه فیثاغورث میباشد.در این قضیه رابطه بین وتر و اضلاع قائم یک مثلث قائم الزاویه بیان میشود. محاسبه مساحت مثلثبرای محاسبه مساحت یک مثلث روشهای مختلفی وجود داردو در ادامه به توضیح این روشها میپردازیم روش هندسیبرای محاسبه مساحت یک مثلث باید طول ارتفاع مثلث و نیز طول قاعده(ضلعی که ارتفاع بر آن عمود است) آن را داشته باشیم.آنگاه میتوانیم از فرمول زیر استفاده کنیم: در این فرمول b طول قاعده و h طول ارتفاع مثلث میباشد. در شکل زیر نحوه بدست آمدن این فرمول بیان شده است: تبدیل مثلث به یک متوازی الاضلاع که دو برابر مثلث مساحت دارد وسپس تبدیل متوازی الضلاع به یک مستطیلبرای پیدا کردن مساحت مثلث (قسمت سبز) ابتدا یک کپی از مثلث (قسمت آبی) را برداشته و آن را 180 درجه میچرخانیم و به مثلث اولیه متصل میکنیم تا یک متوازی الاضلاع بدست آید. با بریدن قسمتی از متوازی الاضلاع و متصل کردن آن به ضلع دیگر آن(همانند شکل) یک مستطیل ایجاد میشود. چون مساحت مستطیل برابر bh است .پس مساحت مثلث اولیه، نصف این مساحت خواهد بود.روش برداری محاسبه مساحت متوازی الاضلاع با استفادهاز ضرب خارجی دو بردارمساحت یک متوازی الاضلاع را میتوان با استفاده از بردارها محاسبه کرد.اگر AB,AC را مطابق شکل فرض کنیم آنگاه مساحت ABCD برابر |AB × AC| خواهد بود.این ...
زاویه و دایره
ط و دایره íزاویه و دایره: زاویه ی مرکزی:زاویه ای که رأس آن مرکز دایره باشد زاویه ی مرکزی نامیده می شود. در شکل مقابل زاویه ی AOB یک زاویه مرکزی است و کمان AB کمان مقابل آن می باشد. نکته: اندازه ی زاویه ی مرکزی با کمان مقابلش مساوی است. زاویه ی مرکزی در دایره: زاویه ی محاطی: زاویه ی محاطی زاویه ای است که رأس آن روی دایره و اضلاع آن دو وتر از همان دایره باشند . در شکل مقابل زاویه ی یک زاویه ی محاطی است و کمان BC ، کمان مقابل آن می باشد. نکته :اندازه ی زاویه ی محاطی نصف کمان مقابل آن است. زاویه ی محاطی در دایره : زاویه ی ظلّی : هر زاویه ای که رأسش روی دایره و یک ضلع آن وتری از دایره و ضلع دیگرش بر دایره مماس باشد ، زاویه ی ظّلی نامیده می شود. در شکل مقابل یک زاویه ی ظّلی و کمان AB کمان مقابل به زاویه ی ظّلی A می باشد. نکته : اندازه ی زاویه ی ظّلی نصف کمان مقابل آن است. زاویه ی ظّلی íمثلث و دایره : دایره ی محاطی مثلث : 3 نیمساز زوایای داخلی مثلث یکدیگر را در یک نقطه مانند o قطع می کنند.می دانیم فاصله ی نقطه ی o از 3 ضلع مثلث به یک فاصله است ؛ یعنی اگر عمودی ها ی OK ،OH و OE را بر اضلاع مثلث فرود آوریم ،داریم : OE=OH=OK پس اگر دایره ای به مرکز O و شعاع OH رسم کنیم ، این دایره در K و H و E بر سه ضلع مثلث مماس خواهد بود . این دایره ، دایره ی محاطی مثلث نام دارد . مرکز دایره ی محاطی مثلث نقطه ی تلاقی نیمساز های زوایای داخلی آن است. محاسبه ی شعاع دایره ی محاطی مثلث: شعاع دایره ی محاطی مثلث را با حرف r نشان می دهیم . دایره ی محیطی مثلث: سه عمود منصف اضلاع یک مثلث بر یک نقطه مانند O می گذرند. می دانیم فاصله ی O از سه رأس مثلث به یک فاصله است، یعنی OA=OB=OC اگر به مرکز O و شعاع مثلأ OA دایره ای رسم کنیم این دایره بر دو رأس دیگر مثلث نیز عبور خواهد کرد . به این دایره ، دایره ی محیطی مثلث می گویند . مرکز دایره ی محیطی مثلث نقطه ی تقاطع عمود منصف های اضلاع آن است. محاسبه ی شعاع دایره ی محیطی مثلث: شعاع دایره ی محیطی مثلث را با حرف R نشان می دهند . در شکل زیر به دو مثلث توجه کنید ؛ این دو مثلث با هم متشابهند . تناسب اضلاع متناظر دو مثلث را می نویسیم: لذا در هر مثلث حاصل ضرب دو ضلع برابر است با : قطر دایره ی محیطی در ارتفاع وارد بر ضلع سوم یعنی : از طرفی می دانیم مساحت مثلث برابر است با : حالا با توجه به رابطه ی (1) و (2) می توان نوشت: دایره و چند ضلعی های متنظم : چند ضلعی متنظم:چند ضلعی که تمام اضلاع آن با هم و همه ی زاویه هایش نیز با هم مساوی باشند یک چند ضلعی متنظم نامیده می شود . مانند مربع که یک چهار ضلعی متنظم است. رسم چند ضلعی متنظم: برای رسم یک n ...
مثلث قائم الزاویه و روابط مثلثاتی
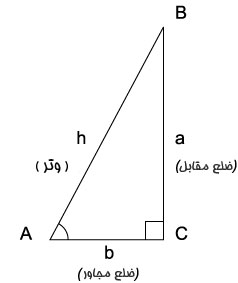
تعریف روی مثلث قائم الزاویه برای تعریف توابع مثلثاتی از یک مثلث قائم الزاویه استفاده می کنیم به عنوان مثال می خواهیم این توابع را برای زاویه A در شکل روبرو تعریف کنیم ما برای استفاده از این مثلث نامگذاری زیر را انجام می دهیم. وتر ضلعی است که روبروی زاویه قائم قرار دار که بلندترین ضلع مثلث نیز می باشد و آن را با h نشان داده شده است. ضلع مقابل زاویه A که آن را با a نشان می دهیم. ضلع مجاور زاویه قائمه که درشکل با b نشان داده شده است.حال توابع مثلثاتی را برای زاویه A روی مثلث ABC تعریف می کنیم. sin: نسبت ضلع مقابل به وتر را سینوس می گویند یعنی: cos: نسبت ضلع مجاور به وتر را گویند یعنی داریم: tangent: نسبت ضلع مقابل زاویه به ضلع مجاور را گویند. cosecant: نسبت وتر به ضلع مقابل زاویه را گویند. secant: نسبت وتر به ضلع مجاور است cotangent: نسبت ضلع مجاور به ضلع مقابل را گویند. تعریف روی دایره واحد در یک صفحه دستگاه مختصات دکارتی، زاویه می تواند هر چهار ربع را طی کند، و مقدار آن می تواند به حسب درجه، گراد رادیان اندازه گیری شود. ضلع متروک این زاویه، دایره با شعاع و مرکز در مبدا، دایره موسوم به دایره واحد یا یک را در نقطه قطع می کند. زاویه در تقاطع محور ها با دایره، مقدار صفر را اختیار می کند این زاویه، طی یک دوران کامل ضلع متحرکش حول مبدا از صفحه شروع و پس از رسیدن به مکان اولیه، دارای زاویه 360 درجه می باشد. روابط مثلثاتی که برای زوایای مختلف برقرار است. برای زوایای بزرگتر از 360 نیز، بر قرار می باشد. مثلا برای دو تابع سینوس و کسینوس خواهیم داشت:
