انتگرال ریمان
انتگرال ریمان

مجموع ریمان: مجموع مساحت مستطیل های که ما برای تخمین مساحت زیر منحنی استفاده می کنیم. مجموع ریمان نامیده می شود. حال با مثالی این مجموع را توضیح می دهیم: تابع:نقاط شروع و پایان بازه: و تعداد مستطیل ها (یا تعداد بازه ها): با استفاده از مجموع ریمان: خواهیم داشت: 11.924959 =مقدار دقیق مساحت 11.8740138= مساحت محاسبه شده بین مجموع ریمان و مقدار دقیق جواب اگر مقایسه ای انجام دهید در این صورت مقدار خطای با برابر خواهد بود با: همانطور که مشاهده شد مستطیل ها به صورت رندومی تولید شده اند و تعداد آنها محدود است. حال به نظر شما اگر تعداد مستطیلها یعنی nرا افزایش دهیم و مستطیل ها، حالت منظم به خود بگیرند چه اتفاقی خواهد افتاد.البته توجه کنید که nهای مختلف، مجموع ریمان مختلفی تولید می کنند. مثال :می خواهیم مجموع ریمان برای مساحت زیر نمودار منحنی دربازه را پیدا کنیم 1) بازه را به 5 قسمت، از تا تقسیم می کنیم: 2) عرض مستطیل ها را پیدا می کنیم. تا3) نقاط را در بین ها برای پیدا کردم ارتفاع مستطیل که برابر با خواهد بود، قرار می دهیم در این صورت: تا 4) پیدا کردن مساحت 5 مستطیل: تا را پیدا میکنیم. 5) مساحت های بدست آمده را با هم جمع می کنیم: انتگرال ریمان: این شکل همگرایی مجموع ریمانرا نشان میدهدهر چه قدر بازه ها کوچکترو تعداد مستطیلها بیشتر میشودمقدار O(حد مجموع بالا)و U (حد مجموع پایین)به مقدار اصلی مساحت نزدیک خواهد شد.ممکن است تا اینجا به این نکته رسیده اید که هر چه قدرعددn (یعنی تعداد مستطیلها) بیشتر باشد مجموع ریمان به یک عدد ،همگرا میشود. یعنی حد گرفتن از مجموع ریمان وقتی که n بسیار بزرگ است مساحت زیر نمودار را به ما می دهد.تعریف انتگرال ریمان:اگر f تابعی باشد که دربازه تعریف شده است در این صورت مجموع ریمان تابعf در بازه وقتی که n به سمت بی نهایت می رود،همگرا به یک مقدار محدود مانند Aخواهد بود. نویسنده
انتگرال ریمان
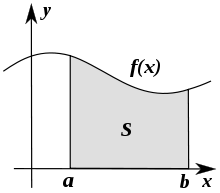
انتگرال ریمان انتگرال سطح زیر یک منحنی در بازه [a,b]. انتگرال ریمان، در آنالیز حقیقی، اولین تعریف دقیق از انتگرال تابع در یک بازه شناخته میشود. این تعریف را برنهارت ریمان ارائه داد. گرچه انتگرال ریمان دارای محدودیتهایی برای بسیاری از مسائل تئوری است، ولی یکی از سادهترین روشهای تعریف انتگرال بوده و بطور گستردهای بکار میرود. تعریف انتگرال ریمان دنبالهای از مجموع ریمان. عدد نمایش داده شده در بالای شکل، سمت راست، برابر با مجموع مساحت مستطیلهای خاکستری است. این مجموع به مقدار انتگرال تابع میل میکند. تقسیم بازه تقسیم بازه [a,b] یک دنباله متناهی به صورت است، که هر یک زیربازه نامیده میشود. اندازه چنین تقسیمی برابر است با طول طولانیترین زیربازه، یعنی: ، .
انتگرال ریمان
این شکل همگرایی مجموع ریمان را نشان میدهدهر چه قدر بازه ها کوچکتر و تعداد مستطیلها بیشتر میشود مقدار O(حد مجموع بالا)و U (حد مجموع پایین) به مقدار اصلی مساحت نزدیک خواهد شد.
انتگرال
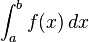
بيش از دو هزار سال پيش ارشميدس (287-212 قبل از ميلاد) فرمول هايي را براي محاسبه سطح وجه ها ، ناحيه ها و حجم هاي جامد مثل كره ، مخروط و سهمي يافت . روش انتگرال گيري ارشميدس استثنايي و فوق العاده بود جبر ، نقش هاي بنيادي ، كليات و حتي واحد اعشار را هم نمي دانست .ليبنيز (1716-1646) و نيوتن (1727-1642) حسابان را كشف كردند . عقيده كليدي آنها اين بود كه مشتق گيري و انتگرال گيري اثر يكديگر را خنثي مي كنند با استفاده از اين ارتباط ها آنها توانستند تعدادي از مسائل مهم در رياضي ، فيزيك و نجوم را حل كنند.فورير (1830-1768) در مورد رسانش گرما بوسيله سلسله زمان هاي مثلثاتي را مي خواند تا نقش هاي بنيادي را نشان دهد .رشته هاي فورير و جابجايي انتگرال امروزه در زمينه هاي مختلفي چون داروسازي و موزيك اجرا مي شود .گائوس (1855-1777) اولين جدول انتگرال را نوشت و همراه ديگران سعي در عملي كردن انتگرال در رياضي و علوم فيزيك كرد . كايوچي (1857-1789) انتگرال را در يك دامنه همبستگي تعريف كرد . ريمان (1866-1826) و ليبيزگو (1941-1875) انتگرال معين را بر اساس يافته هاي مستدل و منطقي استوار كردند .ليوويل (1882-1809) يك اسكلت محكم براي انتگرال گيري بوجود آورد بوسيله فهميدن اينكه چه زماني انتگرال نامعين از نقش هاي اساسي دوباره در مرحله جديد خود نقش اساسي مرحله بعد هستند . هرميت (1901-1822) يك شيوه علمي براي انتگرال گيري به صورت عقلي و فكري ( يك روش علمي براي انتگرال گيري سريع ) در دهه 1940 بعد از ميلاد استراسكي اين روش را همراه لگاريتم توسعه بخشيد . در دهه بيستم ميلادي قبل از بوجود آمدن كامپيوترها رياضيدانان تئوري انتگرال گيري و عملي كردن آن روي جداول انتگرال را توسعه داده بودند و پيشرفت هايي حاصل شده بود .در ميان اين رياضيدانان كساني چون واتسون ، تيچمارش ، بارنر ، ملين ، ميچر ، گرانبر ، هوفريتر ، اردلي ، لوئين ، ليوك ، مگنوس ، آپل بلت ، ابرتينگر ، گرادشتاين ، اكستون ، سريواستاوا ، پرودنيكف ، برايچيكف و ماريچيف حضور داشتند .در سال 1969 رايسيچ پيشرفت بزرگي در زمينه روش علمي گرفتن انتگرال نامعين حاصل كرد . او كارش را بر پايه تئوري عمومي و تجربي انتگرال گيري با قوانين بنيادي منتشر كرد روش او عملاً در همه گروه هاي قضيه بنيادي كارگر نيست تا زماني كه در وجود آن يك معادله سخت مشتق گيري هست كه نياز دارد تا حل شود . تمام تلاش ها ااز آن پس بر روي حل اين معادله با روش علمي براي موفقيت هاي مختلف قضيه اساسي گذاشته شد . ايت تلاش ها باعث پيشرفت كامل سير و روش علمي رايسيچ شد . در دهه 1980 پيشرفت هايي نيز براي توسعه روش او در موارد خاص از قضيه هاي مخصوص و اصلي او شد .از قابليت تعريف انتگرال معين به نتايجي دست ميابيم ...
اندازه و انتگرال لبگ
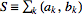
اندازه ی لبگ (Lebesgue Measure)، توسیع مفاهیم طول و مساحت به مجموعه های بسیار پیچیده است. مجموعه ی باز شامل عناصر مجزا (disjoint) (یعنی اشتراک آنها تهی باشد. می توان از انها با عنوان مجموعه های مستقل نیز یاد کرد.)، معلوم است. اندازه ی لبگ به صورت زیر تعریف می شود چنانچه مجموعه ی انتخابی بسته (closed set) باشد یعنی ، آنگاه داریم یک پاره خط به طول واحد، اندازه ی لبگ ۱ دارد، اندازه ی لبگ مجموعه ی کانتور (Cantor set) صفر است. اندازه ی مینکوفسکی (Minkowski measure) یک مجموعه ی بسته کراندار ، در حقیقت همان مفهوم اندازه ی لبگ را در پی دارد (Ko 1995). انتگرال لبگ (Lebesgue Integral) برحسب جملات کران بالا و پایین و بکارگیری اندازه ی لبگ یک مجموعه حاصل می شود. در این تعریف، از جمع لبگ (Lebesgue sum) که در آن مقدار تابع در زیربازه ی و اندازه ی لبگ مجموعه ی ازنقاطی است که برای آنها مقادیر تقریباْ برابر با هستند. این انتگرال، دسته ی عظیمی از توابع انتگرالپذیر که انتگرال ریمان (Riemann integral) آنها را در بر نمی گیرد، را تحت پوشش قرار می دهد. انتگرال لبگ یک تابع در فضای اندازه (measure space) ، به صورت زیر نوشته می شود یا اغلب که تاکیدی بر این موضوع باشد که انتگرال نسبت به اندازه (measure) گرفته می شود. منابع: Croft, H. T.; Falconer, K. J.; and Guy, R. K. Unsolved Problems in Geometry. New York: Springer-Verlag, p. 4, 1991. Kestelman, H. "Lebesgue Measure." Ch. 3 in Modern Theories of Integration, 2nd rev. ed. New York: Dover, pp. 67-91, 1960. Ko, K.-I. "A Polynomial-Time Computable Curve whose Interior has a Nonrecursive Measure." Theoret. Comput. Sci. 145, 241-270, 1995. Kestelman, H. "Lebesgue Integral of a Non-Negative Function" and "Lebesgue Integrals of Functions Which Are Sometimes Negative." Chs. 5-6 in Modern Theories of Integration, 2nd rev. ed. New York: Dover, pp. 113-160, 1960. Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, p. 141, 1984.
انتگرال
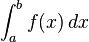
اَنتِگرال (integral) مقدار مشترک ممکن زیرینۀ مجموعهای ریمانی و زبرینۀ مجموعهای ریمانی یک تابع حقیقی در بازۀ مفروض است. انتگرال از مفاهیم اساسی در ریاضیات است که در کنار مشتق دو عملگر اصلی حساب دیفرانسیل و انتگرال را تشکیل میدهند.نخستین بار لایب نیتس نماد استانداردی برای انتگرال معرفی کرد.aو b نقاط ابتدا و انتهای بازه هستند و تابعی انتگرالپذیر است و نمادی برای متغیر انتگرالگیری است.از لحاظ تاریخی یک کمیت بی نهایت کوچک را نشان میدهد. هر چند در تئوریهای جدید، انتگرالگیری بر پایه متفاوتی پایه گذاری شده است.انتگرال نامعینتعریف:هرگاه معادله دیفرانسیلی تابعی معلوم باشد و بخواهیم معادله اصلی تابع را معلوم کنیم این عمل را انتگرال نامعین نامیده و آن را با نماد نمایش میدهند. به انتگرال نامعین ضد مشتق نیز گفته میشود, زیرا عمل انتگرال نامعین گرفتن دقیقا برعکس عملیات مشتقگیری است.بنا به تعریف نماد را انتگرال نامعین نامیده وحاصل آن را تابعی مانند در نظر میگیریم هرگاه داشته باشیم:در واقع میتوان چنین بیان کرد:مثال: مقدار انتگرال تابع را حساب کنید:انتگرال معین بنا به تعریف، نماد را انتگرال معین نامیده و حاصل آن را به ازای عددی به صورت زیر تعریف میکنیم: و به ترتیب، کرانهای بالا و پایین انتگرال نامیده میشوند.تابع انتگرالپذیراگر تابعی دارای انتگرال باشد به آن انتگرالپذیر گویند.تعبیر هندسی انتگرال از نظر هندسی انتگرال برابر است با مساحت سطح محصور زیر نمودار.نکته انتگرال نمودار سه بعدی(انتگرال دو گانه)معرف حجم محصور زیر نمودار است و انتگرال سهگانه معرف پارالل زیر نمودار است(غیرقابل تصور).مثالانتگرال یک تابع مثبت پیوسته در بازه (0,10) در واقع پیدا کردن مساحت محصور بین خطوط x=0 , x=10 و خم منحنی است. aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرالپذیر است و dx نمادی برای متغیر انتگرال گیری است.نمایش گرافیکی انتگرال.انتگرال یک تابع مساحت زیر نمودار آن تابع است.انتگرال گیری محاسبه انتگرال) انتگرال گیری به معنی محاسبه سطح زیر نمودار با استفاده از روشها وقوانین انتگرال گیری است. انتگرال را میتوان عمل برعکس مشتق معرفی نمودمهمترین تعاریف در انتگرال[ویرایش]از مهمترین تعاریف در انتگرال میتوان از انتگرال ریمان و انتگرال لبگ است. انتگرال ریمان بهوسیله برنهارد ریمان در سال ۱۸۵۴ ارائه شد که تعریف دقیقی را از انتگرال ارائه میداد تعریف دیگر را هنری لبگ ارائه داد که طبق این تعریف شرایط تعویض پذیری حد و انتگرال با شرط مساوی ماندن عبارت، ارائه میکرد. از دیگر تعاریف ارائه شده ...
انتگرال و دعوای نیوتن و لایب نیتز
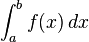
اولین بار لایب نیتس نماد استانداردی برای انتگرال معرفی کرد. aو b نقاط ابتدا و انتهای بازه هستند و تابعی انتگرالپذیر است و نمادی برای متغیر انتگرال گیری است. از لحاظ تاریخی یک کمیت بی نهایت کوچک را نشان میدهد. هر چند در تئوریهای جدید، انتگرال گیری بر پایه متفاوتی پایه گذاری شده است.. از نظر هندسی انتگرال برابر است با مساحت سطح محصور زیر نمودار. نکته انتگرال نمودار سه بعدی(انتگرال دو گانه)معرف حجم محصور زیر نمودار است و انتگرال سهگانه معرف پارالل زیر نمودار است(غیرقابل تصور). مثال انتگرال یک تابع مثبت پیوسته در بازه (0,10) در واقع پیدا کردن مساحت محصور بین خطوط x=0 , x=10 و خم منحنی است. aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرالپذیر است و dx نمادی برای متغیر انتگرال گیری است. نمایش گرافیکی انتگرال. انتگرال یک تابع مساحت زیر نمودار آن تابع است. انتگرال گیری (محاسبه انتگرال) انتگرال گیری به معنی محاسبه سطح زیر نمودار با استفاده از روشها وقوانین انتگرال گیری است. مهمترین تعاریف در انتگرال از مهمترین تعاریف در انتگرال میتوان از انتگرال ریمان و انتگرال لبگ (Lebesgue) است. انتگرال ریمان بهوسیله برنهارد ریمان در سال ۱۸۵۴ ارائه شد که تعریف دقیقی را از انتگرال ارائه میداد تعریف دیگر را هنری لبگ ارائه داد که طبق این تعریف شرایط تعویض پذیری حد و انتگرال با شرط مساوی ماندن عبارت، ارائه میکرد. از دیگر تعاریف ارائه شده در زمینه انتگرال میتوان به انتگرال ریمان-استیلچس (Riemann-Stieltjes) اشاره کرد. پس به طور خلاصه سه تعریف زیر از مهمترین تعاریف انتگرال میباشند: محاسبه انتگرال اکثر روشهای اساسی حل انتگرال بر پایه قضیه اساسی حساب دیفرانسیل و انتگرال بنا نهاده شده است که بر طبق آن داریم: 1.f تابعی در بازه (a,b) در نظر میگیریم. 2.پاد مشتق f را پیدا میکنیم که تابعی است مانند f که و داریم: 3.قضیه اساسی حساب دیفرانسیل و انتگرال را در نظر میگیریم: بنابراین مقدار انتگرال ما برابر خواهد بود. به این نکته توجه کنید که انتگرال واقعاً پاد مشتق نیست (یک عدد است) اما قضیه اساسی به ما اجازه میدهد تا از پاد مشتق برای محاسبه مقدار انتگرال استفاده کنیم. معمولاً پیدا کردن پاد مشتق تابع f کار سادهای نیست و نیاز به استفاده از تکنیکهای انتگرالگیری دارد این تکنیکها عبارتاند از : انتگرال گیری بهوسیله تغییر متغیر انتگرال گیری جزء به جزء : انتگرال گیری با تغییر متغیر مثلثاتی انتگرال گیری بهوسیله تجزیه کسرهاروش هایی دیگر نیز وجود دارد که برای محاسبه انتگرالهای معین به کار میرود همچنین میتوان بعضی از انتگرالها ...
برنهارد ریمان

برنهارد ریمان گئورگ فریدریش برنهارد ریمان (1826-1866) ریاضیدان مشهور آلمانی بود که کارهایش در زمینه آنالیز و هندسه دیفرانسیل و تئوری اعداد بود. ریمان یکی از تاثیرگذارترین ریاضیدانان قرن 19 بود و علی رغم اینکه مجموعه آثار وی از یک جلد بیشتر نیست ولی همین مجموعه آثار شگرفی در ریاضیات پدید آورد. در این کتاب انتگرال ریمان، سطوح ریمان، هندسه ریمان، سری های ریمان و ... آورده شده است. تحقیقات هندسی او بود که نظریه نسبیت آلبرت اینشتین را ممکن ساخت. در سال 1846 وارد دانشگاه گوتینگتن شد و با اقبالی بلند به شاگردی کارل فریدریش گاوس 1777-1855 برجستهترین ریاضیدان معاصرش مفتخر گردید و با ارائه مقالات و طرح مباحث هوشمندانه و خلاقانه توجه وی را به خود معطوف ساخت. در سال 1857 ریمان به سمت استادیاری در گوتینگتن و در سال 1859 استاد آن دانشگاه شد. یکی از شاهکارهای ریمان مقاله ی مهم او راجع به نظریه اعداد است. ریمان در این مقاله به بررسی خواص اعداد اول و ویژگیهای تابعی میپردازد که به تابع زتای ریمان معروف شده است. در این مقاله حدس ریمان را مطرح میکند که امروزه به عنوان مهمترین مساله باز در سرتاسر ریاضی مطرح است. ریمان در سال 1866 و پس از تحمل سالها رنج در سن 39 سالگی در ایتالیا به بیماری سل در گذشت. منبع: وب سایت ویکی پدیا
انالیز ریاضی
آنالیز ریاضی آنالیز شاخه ای از ریاضیات است که با اعداد حقیقی و اعداد مختلط و نیز توابع حقیقی و مختلط سر و کار دارد و به بررسی مفاهیمی از قبیل پیوستگی ،انتگرال گیری و مشق پذیری می پردازد. از نظر تاریخی آنالیز در قرن هفدهم با ابداع حساب دیفرانسیل و انتگرال توسط نیوتن و لایپ نیتس پایه ریزی شد. در قرن هفدهم و هجدهم سر فصل های آنالیزی از قبیل حساب تغییرات،معادلات دیفرانسیل با مشتقات جزئی، آنالیز فوریه در زمینه های کاربردی توسعه فراوانی یافتند و از آنها به طور موفقیت آمیز در زمینه های صنعتی استفاده شد. در قرن هجدهم تعریف مفهوم تابع به یک موضوع بحث بر انگیز در ریاضیات تبدیل شد.در قرن نوزدهم کوشی با معرفی مفهوم سری های کوشی اولین کسی بود که حساب دیفرانسیل و انتگرال را بر یک پایه منطقی استوار کرد.. در اواسط قرن نوزدهم ریمان تئوری انتگرال گیری خود را که به انتگرال ریمان معروف است ارائه داد، در اواخر قرن نوزدهم وایراشتراس مفهوم حد را معرفی کرد و نتایج کار خود بر روی سریها را نیز ارائه داد در همین دوران ریاضیدانان با تلاش های زیاد توانستند انتگرال ریمان را اصلاح نمایند . در اوایل قرن بیستم هیلبرت برای حل معادلات انتگرال فضای هیلبرتی را تعریف و معرفی نمود.از آخرین تحولات در زمینه آنالیز می توان به پایه گذاری آنالیز تابعی توسط یک دانشمند لهستانی به نام باناچ نام برد . آنالیز به دسته های زیر تقسیم بندی می شود :آنالیز حقیقی: به مطالعه بر روی حد ها ،مشتقات،انتگرال ها سریهای توانی می پردازدآنالیز تابعی: به معرفی نظریه هایی از قبیل فضاهای باناچ و نیز فضای هیلبرت می پردازدآنالیز هارمونیک: در این شاخه از آنالیز سری های فوریه مورد مطالعه قرار می گیردآنالیز مختلط: به بررسی توابع مختلط و خواص این توابع از قبیل مشتق پذیری و انتگرال گیری می پردازد آنالیز عددی آنالیز عددی الگوریتم حل مسئله در ریاضیات پیوسته(ریاضیاتی که جدا از ریاضیات گسسته است)را مورد مطالعه قرار میدهد. آنالیز عددی اساسا به مسائل مربوط به متغیرهای حقیقی و متغیرهای مختلط و نیز جبر خطی عددی به علاوه حل معادلات دیفرانسیل و دیگر مسائلی که از فیزیک و مهندسی مشتق میشود. تعدادی از مسائل در ریاضیات پیوسته دقیقا با یک الگوریتم حل میشوند.که به روش های مستقیم حل مسئله معروف اند.برای مثال روش حذف گائوسی برای حل دستگاه معادلات خطی است و نیز روش سیمپلکس در برنامه ریزی خطی مورد استفاده قرار میگیرد. ولی روش مستقیم برای حل خیلی از مسائل وجود ندارد.و ممکن است از روشهای دیگر مانند روش تکرارشونده استفاده شود،چون این روش میتواند در یافتن جواب مسئله موثرتر باشد.تخمین ...
برنهارد ریمان

برنهارد ریمان گئورگ فریدریش برنهارد ریمان (1826-1866) ریاضیدان مشهور آلمانی بود که کارهایش در زمینه آنالیز و هندسه دیفرانسیل و تئوری اعداد بود. ریمان یکی از تاثیرگذارترین ریاضیدانان قرن 19 بود و علی رغم اینکه مجموعه آثار وی از یک جلد بیشتر نیست ولی همین مجموعه آثار شگرفی در ریاضیات پدید آورد. در این کتاب انتگرال ریمان، سطوح ریمان، هندسه ریمان، سری های ریمان و ... آورده شده است. تحقیقات هندسی او بود که نظریه نسبیت آلبرت اینشتین را ممکن ساخت. در سال 1846 وارد دانشگاه گوتینگتن شد و با اقبالی بلند به شاگردی کارل فریدریش گاوس 1777-1855 برجستهترین ریاضیدان معاصرش مفتخر گردید و با ارائه مقالات و طرح مباحث هوشمندانه و خلاقانه توجه وی را به خود معطوف ساخت. در سال 1857 ریمان به سمت استادیاری در گوتینگتن و در سال 1859 استاد آن دانشگاه شد. یکی از شاهکارهای ریمان مقاله ی مهم او راجع به نظریه اعداد است. ریمان در این مقاله به بررسی خواص اعداد اول و ویژگیهای تابعی میپردازد که به تابع زتای ریمان معروف شده است. در این مقاله حدس ریمان را مطرح میکند که امروزه به عنوان مهمترین مساله باز در سرتاسر ریاضی مطرح است. ریمان در سال 1866 و پس از تحمل سالها رنج در سن 39 سالگی در ایتالیا به بیماری سل در گذشت. منبع: وب سایت ویکی پدیا
