اثبات قضیه رول
قضایای متفرقه چند جمله ای ها
-->) این مطلب از بخش آموزش وبسایت المپیاد ریاضی رشد،انتخاب شده که با فرمت pdf نیز در وبسایت المپیاد رشدموجود میباشد. برای مشاهده این موضوعات در وبسایت المپیاد، به آدرس فهرست مطالب ریاضی مراجعه کنید. همچنین میتوانید با کلیک اینجا ، با ویژگیهای بخش آموزش این وبسایت آشنا شوید. قضایای متفرقه چندجملهایها در این فصل چند قضیه نسبتاً مهم که در فصول گذشته امکان آوردنشان نبود را بیان میکنیم. هر چند شاید برخی از این قضیهها به مساله شباهت بیشتری داشته باشند، لکن به علت اهمیت آنها و ایدهای که در حل دارند بصورت قضیه بیان شدهاند. قضیه1 فرض کنید چند جملهای درجه با ریشههای (نه لزوماً متمایز) باشد، ثابت کنید بینو مشتق آن یعنی، رابطه زیر برقرار است اثبات. بسادگی میتوان نوشت که ضریب بزرگترین توان است. اکنون با توجه به فرمول محاسبه مشتق ضرب چندعبارت، میتوان را بدین گونه بدست آورد: -------- که همان صورت قضیه میباشد. مثال1. (لهستان 1979) فرض کنید چند جملهای از درجه است که ریشه حقیقی و متمایز دارد. ثابت کنید: اثبات. با توجه به قضیه قبلی و محاسبه مقدار میتوان نوشت: اگر قضیه درونیابی لاگرانژ را به خاطر آورید، متوجه شباهت بسیاری میان دستور درونیابی لاگرانژ و عبارت فوق که همان میباشد، خواهید شد. اکنون فرض کنید چندجملهای ثابت را بخواهیم با فرمول درونیابی لاگرانژ بسط دهیم: اگر در صورت قضیه قرار دهیم میتوان نوشت: اکنون بوضوح ضریب جمله در دو طرف برابر صفر خواهد بود، لذا در طرف چپ تساوی ضریب را بدینگونه محاسبه میکنیم: که همان رابطه مورد نظر میباشد. پس اثبات مساله به پایان میرسد. قضیه2 فرض کنیدچندجملهای با ضرایب حقیقی باشد به نحویکه برای هر، باشد. ثابت کنید دو چندجملهای با ضرایب حقیقی موجودند که برای آنها داشته باشیم: اثبات. ابتدا نشان میدهیم اگر باشد، آنگاه باید ریشههای حقیقی، همگی دارای مرتبه تکرار زوج باشند. به عبارت دیگر امکان ندارد داشته باشیم ، زیرا در اینصورت با توجه به همواره مثبت بودن، برای داریم و برای داریم، که نتیجه میدهد باید ریشهای از هم باشد، اما این نتیجه با فرض اینکهمقدار تکرار ریشه است، تناقض دارد. لذا باید داشته باشیم که وها ریشههای حقیقی را شامل میشوند ونیز تمام ریشههایش مختلط است. از طرفی بنابر قضیه3 مشاهده میشود که اگر ریشه باشد، مزدوج آن یعنی نیز ریشه خواهد بود، لذا میتوان را بصورت حاصلضرب چندجملهایهای درجه دوم و با ضرایب صحیح تجزیه کرد که هر کدام بدین شکلاند: اکنون با توجه به اتحاد لاگرانژ میتوان گفت که ضرب دو عبارت بصورت یک عبارت ...
مقاله ها و نکات کوتاه و بلند ریاضی
صفحه اصلی وبلاگ (آدرس جدید http://www.ep-math.coo.ir/) دانلود مقاله های تخصصی ریاضیدر این قسمت، جدولهایی را مشاهده خواهید کرد که مربوط به شاخه های مختلف ریاضی است. در هر جدول، مقاله های تخصصی مربوط به آن رشته و نیز خلاصه ای از موضوع مقاله را مشاهده خواهید کرد و در کنار آن محلی برای دانلود مقاله در نظر گرفته شده است. اگر متن مقاله به زبان فارسی باشد، خلاصه آن نیز به زبان فارسی و در غیر اینصورت، خلاصه مقاله به زبان انگلیسی است . تاکنون ۳ مقاله در این جداول گنجانده شده است که به مرور تکمیل خواهد شد، انشاءالله. نکات کوتاه و بلند ریاضیاین قسمت مخصوص مقاله ها و نکات نسبتاْ کوتاه ریاضی در سطح دانشجویان کارشناسی و کارشناسی ارشد ریاضی است. فهرست نکات را در زیر هر بخش، خواهید دید. برای مطالعه یا دانلود مقالات، روی تیتر هر بخش کلیک کنید. نظریه اعداد: شامل ۶ نکته۱. آخرین قضییه فرما برای مکعبها۲. صورت کوتاهی از اثبات آخرین قضیه فرما۳. اثبات دیگری برای قضیه کوچک فرما۴. برهان سلبرگ برای قضیه اعداد اول۵. متن کامل مقاله مهم «اندرو وایلز» (سال ۱۹۹۵) در اثبات قضیه آخر فرما۶. اثبات متعالی بودن دو عدد پی و e ریاضی عمومی: شامل ۹ نکته۱. اثبات اصم بودن عدد پی۲. اثبات اصم بودن عدد e۳. بررسی ریشه های مشتق یک تابع به وسیله قضیه آخر فرما۴. فرمولهایی برای محاسبه عدد پی۵. مجموع توانهای k ام اعداد طبیعی 1، 2،...،n۶. دوازده مقاله کوتاه و جالب پیرامون عدد پی۷. جدول مشتق توابع۸. جدول بزرگ انتگرالهای توابع۹. حل معادلات درجه اول تا چهارم جبر: شامل ۷ نکته۱. کوچکترین چندجمله ای که ریشه آن مجموع ریشه های دوم چند عدد است.۲. اثبات ساده ای از قضیه "کوهن"۳. خاصیت "رول" در میدانهای متناهی۴. حلقه هایی بدون ایده آل ماکزیمال۵. طبقه بندی گروهها از مرتبه ۶۶. گروه متناوب A 4 ، دارای مرتبه ای برابر با ۱۲ است اما زیرگروهی از مرتبه ۶ ندارد.۷. ارتباطی بین نظریه گروهها و نظریه حلقه ها جبر خطی: شامل ۱ نکته۱. از دترمینان تا ماتریس آنالیز ریاضی: شامل ۷ نکته۱. اویلر مقدار تابع زتا در نقطه ۲ را چگونه حساب کرد؟۲. مقاله زیبایی پیرامون تابع زتا۳. عدد ثابت اویلر۴. کران بالا و پایین برای ریشه های یک چند جمله ای با ضرایب مختلط۵. آشنایی با روش پوشش تمام در آنالیز حقیقی۶. نکاتی پیرامون مثبت بودن مشتق یک تابع پیوسته و یکنوایی آن۷. برهانهای دیگری برای چند قضیه آنالیز مقدماتی
قضیه ی دزارگ
هِندِسه مطالعه انواع روابط طولی و اشکال و خصوصیات آنها است. این دانش همراه با حساب یکی از دو شاخه قدیمی ریاضیات است. واژه هندسه عربی شده واژه «اندازه» در فارسی است. در زبان انگلیسی به آن geometry و در زبان فرانسه به آن géométrie میگویند که هردو از γεωμετρία (گئومتریا) در زبان یونانی آمده که به معنای اندازهگیری زمین است.تاریخچه هندسهاحتمالاً بابلیان و مصریان کهن نخستین کسانی بودند که اصول هندسه را کشف کردند. در مصر هر سال رودخانه نیل طغیان میکرد و نواحی اطراف رودخانه را سیل فرا میگرفت. این رویداد تمام علایم مرزی میان املاک را از بین میبرد و لازم میشد دوباره هر کس زمین خود را اندازهگیری و مرزبندی کند. مصریان روش علامتگذاری زمینها با تیرک و طناب را ابداع کردند. آنها تیرکی را در نقطهای مناسب در زمین فرو میکردند و تیرک دیگری در جایی دیگر نصب میشد و دو تیرک با طنابی که مرز را مشخص میساخت به یکدیگر متصل میشدند. با دو تیرک دبگر زمین محصور شده و محلی برای کشت یا ساختمان سازی مشخص میشد.در آغاز هندسه برپایه دانستههای تجربی پراکندهای در مورد طول و زاویه و مساحت و حجم قرار داشت که برای مساحی و ساختمان و نجوم و برخی صنایع دستی لازم میشد. بعضی از این دانستهها بسیار پیشرفته بودند مثلاً هم مصریان و هم بابلیان قضیه فیثاغورث را ۱۵۰۰ سال قبل از فیثاغورث میشناختند. یونانیان دانستههای هندسی را مدون کردند و بر پایهای استدلالی قراردادند. برای آنان هندسه مهمترین دانشها بود و موضوع آن را مفاهیم مجردی میدانستند که اشکال مادی فقط تقریبی از آن مفاهیم مجرد بود. در سال ۶۰۰ قبل از میلاد مسیح، یک آموزگار اهل ایونیا (که در روزگار ما بخشی از ترکیه بهشمار میرود) به نام طالس، چند گزاره یا قضیه هندسی را به صورت استنتاجی ثابت کرد. او آغازگر هندسه ترسیمی بود. روش استنتاجی روشی است علمی (بر خلاف روش استقرایی) که در آن مسالهای به وسیلهی قضایا و حکمها ثابت می گردد. فیثاغورث که او نیز اهل ایونیا و احتمالاً از شاگردان طالس بود توانست قضیهای را که بهنام او مشهور است اثبات (ریاضی) کند. البته او واضع این قضیه نبود. اما دانشمندی به نام اقلیدس که در اسکندریه زندگی میکرد، هندسه را به صورت یک علم بیان نمود. وی حدود سال ۳۰۰ پیش از میلاد مسیح، تمام نتایج هندسی را که تا آن زمان شناخته بود، گرد آورد و آنها را به طور منظم، در یک مجموعه ۱۳ جلدی قرار داد. این کتابها که اصول هندسه نام داشتند، به مدت ۲ هزار سال در سراسر دنیا برای مطالعه هندسه به کار میرفتند. براساس این قوانین، هندسه اقلیدسی تکامل ...
آشنایی با جبر از مقدماتی تا پیشرفته
جبر مجرد مقدماتی،اشیاء و اعمال ریاضی را،فارغ از ماهیت آنها بررسی می کند. اعداد، توابع، ماتریسها،از عناصر آن و اعمال دوتایی ضرب،ترکیب توابع و ... از اعمال آن به شمار می آیند.دسته بندی گروهها و حلقه ها از موضوعات اساسی این شاخه به حساب می آیند.برخی شاخه های هندسی با جبر مجرد ارتباط پیدا می کنند. جبر مقدماتی بهمراه جبر مجرد و جبر خطی سه شاخه ی اصلی دستگاه جبر را تشکیل میدهند تجرید (Abstraction) در ریاضیّات از فرآیند تشخیص و استخراج یک جوهره و مفهوم ریاضی اصلی، کلّی، و فراگیر شروع میشود. چنانچه وجود و حضور این جوهره و مفهوم خاصّ در تک تک موارد جزئی مورد بررسی صادق باشد، امر اختصار و سادهتر کردن عبارات را میتوان با جدا نمودن و حذف جزئیّات گوناگون از این لایه خاصّ ادامه داد. برای مثال، میتوان عبارت زیر را در نظر گرفت: دو میز + دو کتاب + دو قلم + دو لیوان + دو دفتر + دو خط کش + ... جهت اجراء فرایند تجرید، میشود مفهوم دو تا بودن را که در مورد همهء جملهها صدق میکند، از میان برداشته و آنرا در لایهی بالاتری قرار داد. عبارت فوق خواهد شد: دو(میز + کتاب + قلم + لیوان + دفتر + خط کش + ...) عبارت جدید کوتاهتر شده است، و مفهوم کلّی تر عدد دو بودن که در آن مجرّد و مجزا شده، هنوز هم به همهء جملات جزئی در درون پرانتز تعلّق دارد. همین کار را، حالا می شود با اعداد دیگر مثل سه، چهار، پنج، شش، و ... تکرار کرد. پس، تراز و لایهای نو پدیدار گردیدهاست که در آن فقط مفاهیم مجردی به این صورت قرار دارد: دو، سه، چهار، پنج، شش، ... از خود میپرسیم، حالا چه جوهرهء مشترک کلّیتری را میشود از این لایهء جدید جدا کرد؟ جواب: مفهوم عامّتر و همهجاگیرتر عدد طبیعی بودن را؛ هر عدد طبیعیی بودن را. این همان شروع و آغاز جبر است. از همین نقطه است که مفهومی مجرّد و ذهنی موسوم بهمتغیّر تولّد می یابد. مطالب وابسته تجرید جبر مجرّد اعداد صحیح اعداد گویا حلقه ها :گسترش در ریاضیات و جبر مجرد، حلقهای را که در آن عمل ضرب خاصیت جابجایی داشته باشد، حلقه جابجایی میگویند. حلقه ها حلقه گروهی آبلی جمعی بانضمام نیمگروهی ضربی است که ضرب نسبت به جمع توزیعپذیراعداد صحیح این ویژگی را دارند. اگر نیمگروه ضربی مونوئید باشد حلقه را یکدار گوییم و اگر جابجایی باشد حلقه را جابجایی گوییم باشد. مثلاً + نوشته شده در پنجشنبه سیزدهم تیر 1387ساعت 12:45 بعد از ظهر توسط مجید | نظر بدهید نظریه حلقه ها- اعداد صحیح مجموعهٔ اعداد صحیح به اجتماع مجموعهٔ اعداد طبیعی، قرینهٔ اعداد طبیعی ، و {0} (مجموعهصفرعضو ...
/تجربی ها و تهدید!!!/ سرشماری 6 /یک آدم فضایی/ک مثل کاوالیری/هندسه 1/ جواب مساله+تشکر/
<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" /> 1) از خودمون خیلی جای تعجب داره که خواهر آدم قالب نویس و مخ HTML باشه اما آدم یه قالب درست حسابی وبلاگش نداشته باشه!!! و بخواد تهدید های مکرر بعضیا رو در مورد قالب بشنوه!!! *راستی بنده همین جا اعلام می کنم نتایج ششمین سرشماری ملی از اعتبار کافی برخور دار نیست! چون مامانم اینا همسایه ی طبقه ی پایینمونو جا انداختن!!!! 2) از خودمون و از ریاضی و اما سوال پست پیش، با تشکر از آقای افشین منش (ریاضیات زیباست)و آقای اسماعیلی فر (لبخند ریاضی) بخاطر اثبات های قشنگی که کرده بودن... من فکر می کردم تعداد بیشتری به مساله جواب بدن! جواب مساله: الف) اثبات با استفاده از اصل لانه کبوتر اگر در میهمانی کسانی را که دست می دهندn در نظر بگیریم و به کسانی که دست نمی دهند کاری نداشته باشیم هر نفر n-1 بار یا کمتر دست می دهد (چون با توجه به صورت سوال کسی با خودش دست نمی دهد... ) حالا اگر n نفر را کبوتر و تعداد دست دادن ها که n-1 حالت دارد: n-1), (n-2), (n-3),… , 1})} ، را لانه در نظر بگیریم طبق اصل لانه کبوتری حداقل دو نفر وجود دارند که تعداد دست دادن هایشان با هم برابر است. ب) اثبات با کمک گراف جواب دوستانمون اونقدر کامل بود که دیگه من هیچی نمی گم و جوابشونو براتون می نویسم. آقای افشین منش: اگر درجه تمام روس زوج باشد که هیچ. (چون حتما دو راس با درجه مساوی خواهیم داشت- با توجه به نوع مساله). اما اگر یک راس درجه فرد داشته باشیم آنوقت الزاما باید راس دیگری از درجه فرد وجود داشته باشد (زیرا تعداد رئوس با درجه فرد در یک گراف، عددی زوج است). آقای اسماعیلی فر: اگر هر نفر رو یک راس بگیریم و هر دست دادن رو یک یال بین اونها اون وقت مساله گرافیکال میشه. حالا چون تو این گراف طوقه نداریم(کسی با خودش دست نمیده) و این گراف چندگانه است(هیچ دو نفری دوبار یا بیشتر با هم دست نمی دهند) لذا گراف حاصل گراف ساده ست. تعداد دست دادن ها براي هر نفر هم معادل درجه گراف مفروضه. قضیه: هر گراف ساده n راسي G، با حداقل دو راس داراي دو راس با درجه برابر است. اثبات: مي دانيم درجه هر راس گراف G متعلق به مجموعه 0و1و ... n-1 است. اگر دو راس از درجه برابر باشند حكم برقرار است. در غير اينصورت (فرض خلف) همه اعداد فوق درجه راسي از گراف G خواهند بود (واضحه كه با اين فرض درجه هيچ دوراسي برابر نيست). مخصوصا اينكه دو راس وجود دارند كه يكي از درجه صفر و يكي از درجه n-1 است كه اين يه تناقضه(چون اگه يك راس درجه اش n-1 باشه اونوقت به همه رئوس ديگر يك يال داره و لذا درجه بقيه رئوس حداقل يك است و صفر بودن درجه يكي از رئوس با اين مطلبي كه بيان كرديم در تناقضه). پس فرض خلف باطل است و لذا ...
اصل کاوالیری
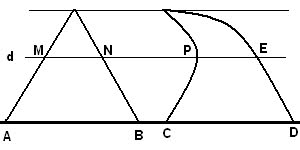
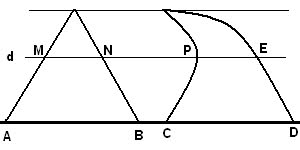
<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" /> بوتاون تورا کاوالیری (1564-1642) اهل میلان، از همان سال های نخستین به ریاضیات علاقه مند بود،و به ظاهر زیر تاثیر گالیله، روش « غیر قابل تقسیم ها» را در هندسه بوجود آورد که در اثر بزرگ او در سال 1635، با عنوان «هندسه، با طرح تازه ای بر اساس غیر قابل تقسیم های پیوسته»، به شهرت رسید. غیر قابل تقسیم ها، از نظر کاوالیری، وترهای موازی در درون شکل روی صفحه، و صفحه های موازی در درون جسم بود. او برای مقایسه ی شکل های روی صفحه و جسم های فضایی، مفهوم « مجموع همه ی غیر قابل تقسیم ها» را آورد که تماس سطح و فضای جسم را پر می کردند. برای کاوالیری، نسبت این مجموع ها، همان نسبت مساحت ها و حجم ها بود. او شکل های روی صفحه را، بین دو خط راست موازی در نظر گرفت. اصل کاوالیری درباره مساحت: اگر فرض کنیم قاعده های دو شکل بر روی یک خط قرار گرفته باشند. اگر هر خطی موازی قاعده های دو شکل در آنها قطعه هایی با طول های مساوی ایجاد کند، مساحت های آن دو شکل برابر است. با توجه به شکل دو شکل بر روی افق قرار گرفته اند. اگرهر خطی به موازات قاعده مانند d رسم کنیم و داشته باشیم: AB=CD، MN=PE ، آنگاه دو شکل هم مساحت هستند. <?xml:namespace prefix = v ns = "urn:schemas-microsoft-com:vml" /> اصل کاوالیری در باره حجم ها: دو شکل فضایی و صفحه ای که قاعده های دو شکل در آن قرار گرفته باشد را نظر بگیرید. اگر هر صفحه ای موازی با این صفحه که یکی از این دو شکل را قطع می کند، دیگری را نیز قطع می کند و سطح مقطع های حاصل دارای مساحت های برابر باشند، آنگاه این دو شکل فضایی حجم یکسان دارند. خود کاوالیری در این زمینه می نویسد: «دو جسمی که قاعده ی آنهای بر یک صفحه و ارتفاعشان برابر باشد، به شرطی هم ارزند یعنی حجم های برابر دارند که مقطع های آنهابا صفحه های موازی با قاعده باشد.» این نظام کار، به نام «نظام کاوالیری» معروف است. کاوالیری بر پایه ی این نظام، قضیه های زیادی را اثبات می کند. برای نمونه، ثابت کرد نسبت مساحت های دو مثلث متشابه برابر است با نسبت مجذور ضلع های متناظر آن ها. ابهامی که در مفهوم «مجموع غیر قابل تقسیم ها» وجود دارد، موجب اعتراض و انتقاد سخت بعضی از هم عصران کاوالیری شد. به همین خاطر کاوالیری کتاب دیگری با نام «شش طرح هندسی» را نوشت که در آن، تلاش کرد مفهوم هایی را که بکار می برد، دقیق تر کند، با وجود این، خود کاوالیری تا پایان زندگی نسبت به کافی بودن استدلالهای خود در تردید باقی بود، گرچه به درستی آن ها اعتقاد داشت. طرح کاوالیری در هندسه و آموزش او درباره ی غیر قابل تقسیم ها، تنها برای درک بهتر هندسه ی مقدماتی سودمند نبود. این آموزش، یعنی جمع کردن ...
مساحت کاوالیری
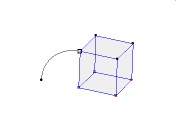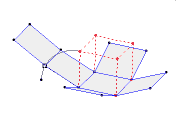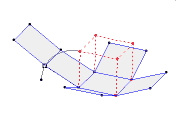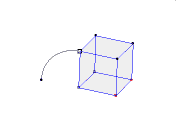
هدف از این نوشته آشنایی شما با اصل مساحت کاوالیری است. اگر فرض کنیم قاعده های دو شکل بر روی یک خط قرار گرفته باشند. اگر هر خطی موازی قاعده های دو شکل در آنها قطعه هایی با طول های مساوی ایجاد کند، مساحت های آن دو شکل برابر است.با توجه به شکل دو شکل بر روی افق قرار گرفته اند. اگرهر خطی به موازات قاعده مانند d رسم کنیم و داشته باشیم: AB=CD، MN=PE ، آنگاه دو شکل هم مساحت هستند. اصل حجم کاوالیری دو شکل فضایی و صفحه ای که قاعده های دو شکل در آن قرار گرفته باشد را نظر بگیرید. اگر هر صفحه ای موازی با این صفحه که یکی از این دو شکل را قطع می کند، دیگری را نیز قطع می کند و سطح مقطع های حاصل دارای مساحت های برابر باشند، آنگاه این دو شکل فضایی حجم یکسان دارند.خود کاوالیری در این زمینه می نویسد: «دو جسمی که قاعده ی آنهای بر یک صفحه و ارتفاعشان برابر باشد، به شرطی هم ارزند یعنی حجم های برابر دارند که مقطع های آنهابا صفحه های موازی با قاعده باشد.»این نظام کار، به نام «نظام کاوالیری» معروف است.کاوالیری بر پایه ی این نظام، قضیه های زیادی را اثبات می کند. برای نمونه، ثابت کرد نسبت مساحت های دو مثلث متشابه برابر است با نسبت مجذور ضلع های متناظر آن ها.ابهامی که در مفهوم «مجموع غیر قابل تقسیم ها» وجود دارد، موجب اعتراض و انتقاد سخت بعضی از هم عصران کاوالیری شد. به همین خاطر کاوالیری کتاب دیگری با نام «شش طرح هندسی» را نوشت که در آن، تلاش کرد مفهوم هایی را که بکار می برد، دقیق تر کند، با وجود این، خود کاوالیری تا پایان زندگی نسبت به کافی بودن استدلالهای خود در تردید باقی بود، گرچه به درستی آن ها اعتقاد داشت.طرح کاوالیری در هندسه و آموزش او درباره ی غیر قابل تقسیم ها، تنها برای درک بهتر هندسه ی مقدماتی سودمند نبود. این آموزش، یعنی جمع کردن غیر قابل تقسیم ها، پیش در آمدی برای انتگرال گیری بود. کاوالیری نماد انتگرال را بکار نمی برد، ولی در واقع از انتگرال گیری استفاده می کرد…به جز این، در هندسه ی کاولیری به قضیه هایی بر می خوریم که برای پیدایش محاسبه ی دیفرانسیلی، ارزش معینی دارند. از آن جمله، نخستین گزاره ای که در هندسه آمده، هم ارز با قضیه رول است، و به دنبال آن گزاره ای آمده است که مضمون آن اینست: در نقطه های ماکزیمم و می نیمم تابع، مماس بر نمودار با محور طول ها موازی است.یکی از کمبود های جدی هندسه ی کاوالیری این است که مولف از بکارگیری جبر فراری است و همه جا به هندسه دانان قدیمی تکیه می کند. بی تردید، بکار گیری نمادهای جبری که در زمان کاوالیری رایج شده بود، می توانست کارهای او را دقیق تر، کامل تر و قابل درک تر کند.
سفسطه های هندسی ابتدایی/Geometric fallacy
هرزمان وهرجا نامی از اقلیدس به میان آید، همیشه هندسه وکتاب مقدمات هندسه ی او به خاطرمی آید.جای شگفتی است که بیشتر گمان می رود اقلیدس، تنها پیرامون هندسه به کار پرداخته ومقدمات هم تنها کتاب او بوده است.درحا لی که این هندسه دان یونا ن با ستان، درباره ی موسیقی و رشته ها ی دیگر فیزیک نیز آثاری داشته که به دوازده کتا ب و رساله می رسیده اند. باگذشت زمان ، برخی از آنها بطور کلی نیست و نابود شده اند وبرخی دیگر که از گزند روزگار مصون مانده اند ، تنها پنج اثر می باشند که به د ست ما رسیده اند. ازمیان کتب از د ست رفته می توان پسوداریا (Pseudaria) را نام برد . از اسم کتا ب بر می آید که مجموعه ای از سفسطه های هندسی را در بر می گرفته است.گمان می رود، این کتاب، استدلالهای نادرستی را مورد بحث قرار داده باشد که منتج به قضایای نادرست می شوند وبه آسانی اشتباه خود را آشکار نمی کنند. از زمان اقلیدس تا کنون نیز صدها سفسطه ی هندسی انتشار یافته که در برخی از آنها خطاهای پنهانی و زیرکانه به کار رفته و در پاره ای دیگر، افکار و اندیشه های کارساز. در اینجا چهارنمونه از این سفسطه ها را می آوریم که بهترین قضیه های نادرست را در بر می گیرند.این قضا یا به دانشی بیش از هندسه ی مقدماتی مسطحه نیازی ندارند و چه بسا در پسوداریا ی اقلیدس نیز آمده اند. هر مثلثی متساوی الساقین است: این امر نا ممکن و شگفت انگیز از کتاب تصویر لوئیز کا رول گرفته شده است.کارول،این قضیه رابه احتمال زیاد، برای اولین بار در سال 1882 منتشر کرده بود.او،این قضیه را با مهارتی خاص در کتابش به اثبات رسانده است. صورت مساله: مثلث نا مشخص ABC را در نظر می گیریم.DE عمود منصف ضلع BC را رسم می کنیم.نیمساز زاویه ی A را نیز رسم می کنیم.دوحالت پیش می آید: 1) ممکن است نیمساز،عمود منصف را قطع نکند.دراین صورت با آن موازی ودر نتیجه بر BC عمود خواهد بود؛ یعنی نیمساز A بر ارتفاع مثلث منطبق می شود،واین، تنهادرمثلث متساوی الساقین است که نیمساز زاویه ی بین دو ساق، بر ارتفاع واقع است. 2) در حالتی که نیمساز زاویه ی A ، خط DE را در نقطه ای مثل F قطع کند . در این صورت از نقطه ی F ، خطهای راست FB و FC رارسم می کنیم،همچنین از نقطه ی F دوخط FG و FH را به ترتیب عمود بر AC و AB می کشیم. دراین جا ، دومثلث قائم الزاویه ی AFG و AFH برابرند ، زیرا در ضلع AF مشترک هستند و زوایا ی FAG و AGF به ترتیب با زاویه های FAH و AHF برابرند و در نتیجه: AH=AG و FH=FG . دو مثلث قائم الزاویه ی BDF و CDF نیز با هم برابرند ؛ زیرا ، BD=DC و ضلع DF بین آنها مشترک و د و زاویه قائمه ی D نیز برابرند؛ پس، FB=FC . در مثلث قائم الزاویه ی FHB داریم:مربع وتر FB مساوی است با مجموع مربعات ...
نویسنده مهمان : لادن

ذولی: همونطور که قبلا قول داده بودم امروز یه پست از یه نویسنده ی مهمان میذارم که لطف کرد و این مطلب رو برای وبلاگ من نوشت. امیدوارم خوشتون بیاد. این نویسنده ی خوب کسی نیست جز .... لادن !! *** لادن: نمیدونم از کجا شروع کنم ، راستش چند وقت پیش تو وبه یکی از دوستام یه دعوایی بین دپیست ها (طرفداران پر و پا قرص جانی دپ) راه افتاد که بیا و ببین ، این طرفدارای تازه کار چون با اخلاقه جانی آشنایی کامل ندارن و به خاطر اینکه این بشر لاک آبی یا سیاه می زنه اعتقاد پیدا کردن که جانی شیطان پرسته. یا بعد از جدایی جانی دپ از همسر قبلیش خیلی ها براش حرف در آوردن که آدم بی بند و باریِ و هر روز با یک دختر جدیده. اولا ؛ جانی به هیچ وجه شیطان پرست نیست و یک مسیحی معتقده و بارها نشون داده که به همه ی ادیان احترام میذاره . یکی از اعتقادات شیطان پرستان اینه که برای ازدواج و خانواده هیچ ازرشی قائل نیستن ، در حالی که جانی خانواده تشکیل داده و دو تا بچه هم داره. لاک زدن هم دلیلی برای اثبات شیطان پرستی جانی نیست. جانی دپ بارها و بارها در کنسرت های راک اند رول شرکت کرده و در مصاحبه هاش اعلام کرده که انتخاب اولش خوانندگی و نوازندگی در گروه های راک اند رول بوده. لاک زدن خاصه ی گروه های راک اند روله و جانی هم به علت علاقه ی زیادی که به این سبک موسیقی داره و یجورایی شخصیت راکی داره، لاک میزنه. یه مثال دیگه هم میتونه "آدام لمبرت" باشه که یهودیه اما به خاطر علاقه به موسیقی راک ، لاک میزنه. دوما ؛ اونایی که میگن جانی بی بند و باره آیا زندگی مشترک 14 ساله ی او و ونسا (همسر قبلیش) رو فراموش کردن ؟ جانی دپ تو این دوره ی محبوبیتش کم حاشیه ترین بازیگر هالیوود بوده که بازی های بی نقصی ارائه داده. جدایی های جانی از دوست دخترهاش همیشه به دلیل مسائل شخصی بوده و این مرد هیچوقت به هیچ کدوم از اونها خیانت نکرده. یکی از اون مسائل شخصی مسئله ی بچه دار شدن بوده که بین همه ی دوست دخترهای قبلیش فقط ونسا قبول کرده بچه دار بشه ؛ به همین دلیل بود که جانی عاشق ونسا شد و 14 سال باهاش زندگی کرد. چرا بعضی ها نمی تونن موفقیت بقیه رو ببینن ؟ چرا دوست دارید فقط برای بقیه حاشیه درست کنید؟ مثلا چرا قضیه ی دوستی جانی با امبر هرد رو انقدر بزرگش کردید ؟ مگه جانی آدم نیست و احتیاج به همدم نداره؟ بابا اونم آدمه و زندگیه خودشو داره ، تازه زندگیش هم که تابحال به اون بدی نبوده که بقیه ی هالیوودیا بودن ، اون یه مرد مهربونه که عاشقه خانوادس و به همه ی طرفداراشم احترام میذاره پس چرا باید بهش گیر بدیم؟؟؟؟؟؟؟ جنتلمن و با وقار و با شخصیت هم هست ، پسر خوبیه ! و در ادامه باید بگم که اگه بد بود این همه طرفدار ...
