آموزش ماتریس
ماتریس
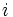
ماتریس ماتریس عبارت است از آرایشی (آرایهای) مستطیل شکل از اعداد مختلط به طوری که عناصر این آرایه را درایه مینامیم و عنصر واقع در سطر ام و ستون ام را با نماد نشان میدهیم. ماتریسی که دارای سطر و ستون باشد را ماتریس از مرتبه در مینامیم.( ) نکته هرگاه آنگاه ماتریس را مربع از مرتبه مینامیم. یک ماتریس را بصورت نمایش میدهیم. تاریخچه مطالعه روی انواع خاصی از ماتریسها مانند مربعهای جادویی و مربعهای لاتین ، به تاریخ قبل از میلاد نسبت داده شده است. معرفی و تکامل نمایش ماتریسها به عنوان شاخهای از جبر خطی در نتیجه مطلعه روی ضرایب سیستم معادلات خطی و الگوها و روشهای حل آنها بوجود آمد. لایب نیتس به عنوان یکی از پایه گذاران علم حسابان در سال 1693، دترمینان ماتریسها را معرفی کرد. در ادامه کرامر روش خود را برای حل دستگاه معادلات خطی بر اساس دترمینان ماتریس ضرایب دستگاه معرفی کرد. این روش که به روش کرامر مرسوم است، بر اساس استفاده صریح از دترمینان ماتریس ضرایب معرفی گردیده است. در مقابل اولین استفاده ضمنی از ماتریسها توسط لاگرانژ برای تعیین ماکزیمم و مینیمم توابع چند مقداری مورد استفاده قرار گرفت. در ادامه گاوس روش حذفی خود را برای حل مسائل کمترین مربعات که کاربردهای بسیار وسیعی در علوم سماوی و ژئودوزی دارد را معرفی کرد. روابط بین ماتریسها تساوی دو ماتریس دو ماتریس و مساوی اند اگر و فقط اگر (هم مرتبه باشند) و جمع دو ماتریس اگر و آنگاه قرینه ماتریس اگر آنگاه قرینه را بصورت زیر تعریف میکنیم: ضرب اسکالر در ماتریس اگر و یک اسکالر باشد آنگاهدر ضرب اسکالر یک عدد در یک ماتریس ضرب میشود. در این نوع ضرب تمامی عناصر ماتریس در آن عدد ضرب میشوند به عنوان مثال: و نمایش ریاضی آن به صورت زیر می باشد: cA)ij = c(A)ij) ضرب ماتریسها اگر و آنگاه ضرب دو ماتریس را با علامت نمایش داده و بصورت زیر تعریف خواهیم کرد: در این نوع هر دو ضرب شونده و ضرب کننده از نوع ماتریس میباشند. بطور مشابه ضرب دو ماتریس نیز باید یک جنبه خوش تعریفی داشته باشد. ضرب دو ماتریس داده شده A و B زمانی خوش تعریف است که تعداد ستونهای ماتریس ضرب کننده با تعداد سطرهای ماتریس ضرب شونده برابر باشند. بر این ضرب دو ماتریس که شرایط قابل ضرب بودن را داشته باشند به صورت زیر بیان میشود: برای بدست آوردن عنصر روی سطر iام و ستون y ام ماتریس خاصل ضرب عناصر روی سطر iام ماتریس ضرب کننده و عناصر روی ستون j ام ماتریس ضرب شونده را در نظر گرفته و آنها در هم ضرب و جمع می کنیم. به صورت ریاضی حاصلضرب دو ماتریس بصورت زیر نمایش داده می شود: A × B)ij = (A)i1(B)1j + (A)i2(B)2j + ... + ...
جدول ماتریسی (swot)
به نام خدا تدوین استراتژیها یا راهبردها در سیاستهای کلان فرآیند مشارکت در منطقه (مدرسه)، ایجاب می کنند که از وجود فرصتها برای کاهش تهدیدها و از وجود قوتها جهت رفع ضعفها بهرهمند شد و با مشارکت اولیا و حمایتهای موجود در منطقه (مدرسه) تهدیدها را کاهش داد. بنابراین ابتدا باید فرآیندها خوب شناسایی شوند و پس از اولویت بندی مورد تجزیه و تحلیل قرار گیرند. آنگاه در ماتریس سوات (swot) تجزیه وتحلیل شده و پس از تدوین راهبردها اقدام لازم به عمل آید. این امر کمک میکند تا در برنامهریزی، اجرا، ارزشیابی و اقدام دچار مشکل نشویم. (توراني.حيدر، 1384) جدول (1ـ5): ماتریس (swot) فرآیند بهبود افت تحصیلی دانشآموزان ماتریس SWOT فرصتها O تهدیدها T قوتها(S) Strengths ـ قانون برنامه چهارم توسعه اقتصادی، اجتماعی ـ سند توسعه آموزش و پرورش در برنامه چهارم ـ وجود مراکز علمیدانشگاهی در مناطق و شهرهای همجوار ـ پشتیبانی سازمان آموزش و پرورش، شورای آموزش و پرورش استان ـ وجود شورای اسلامیشهر و روستا ـ وجود کمیتهی امداد امام خمینی و سایر نهادهای حمایتی ـ فقر فرهنگی و کم سوادی خانوادهها ـ فقر اقتصادی خانوادهها ـ نبود کتابخانهي مرکزی ـ نبود ارتباط با مراکز علمیو دانشگاهی فرصتها(O) Opportunities ضعفها(W) Weaknesses تهدیدها(T) Threats جدول (2ـ5): ماتریس (swot) قوتها S استرتژیها SO استراتژی ST ـ شواری آموزش و پرورش استان و منطقه ـ معلمان با انگیزه و مجرب ـ تجربه مدارس موفق ـ انعطاف در تحصیل دانشآموزان مناطق کم جمعیت (آموزش از راه آموزش نیمه حضوری) ـ شورای مدرسه، معلمان، شورای دانش آموزی و انجمن اولیاء و مربیان ـ نظام ارزشیابی کارکنان ـ وجود پنجره باز در برنامههای هفتگی مدارس ـ شناسایی و بهرهگیری از ظرفیتها و امکانات درون و بیرون منطقه ای ـ سازمان دهی نیروی انسانی علاقمند و بهرهگیری از ظرفیت مدارس موفق ـ متنوع نمودن شیوههای آموزش و پرورش دانشآموزان با همکاری سازمان آموزش و پرورش ـ برنامهریزی و تشکیل کلاسهای آموزش جبرانی و علمي طول سال تحصیلی ـ افزایش آگاهی اولیاء دانشآموزان ـ پیشنهاد ایجاد کتابخانهي مرکزی به وزارت ارشاد، شهرداری و سایر مراجع ذيربط جدول (3ـ5): ماتریس (swot) ضعفها W استراتژی WO استراتژی WT ـ روشهای نامناسب مطالعه دانشآموزان ـ روشهای تدریس نامناسب برخی معلمان ـ استاندارد ...
اموزش متلب_ماتریس ها
تمامی داده ها در متلب به صورت ماتریس ذخیره میشود.حتی اعداد اسکالر به صورت یک ماتریس 1در1 ذخیره میشوند.ارایه های ماتریس هارا در متلب بین دو لامت [] تعریف میکنند>> a=[1 2 3]a = 1 2 3>> b=1:1:3b = 1 2 3>> c=linspace(1,3,3)c = 1 2 3نکته:دستور (linspace(a,b,n بازه[a,b] رابه n قسمت مساوی تقسیم میکند>> d=[1:3]d = 1 2 3>> e=1:3e = 1 2 3تمامی دستورات ماتریسی به یک اندازه تولید کرده اند با اجرای دستور whos میتوانید متغیرهای داخل workspace را بررسی کنید.>> whos Name Size Bytes Class Attributes a 1x3 24 double b 1x3 24 double c 1x3 24 double d 1x3 24 double e 1x3 24 double >> a=[1 2;3 4;5 6]a = 1 2 3 4 5 6ماتریس فوق ماتریسی است 2*3 که شامل 4 عنصرمیباشد>> a=[1 2 3 4]a = 1 2 3 4این یک ماتریس 4*1 (ملقب به بردار سطری)است که شامل 4 عنصر میباشد>> a=[1;2;3;4]a = 1 2 3 4این یک ماتریس 1*4(ملقب به ماتریس ستونی)است که شامل 4 عنصر میباشداز مثالهای فوق متوجه شدیم که با استفاده از ";"(سمیکالن) سطرهارا جدامیکنیم.هر دو دستور زیر یک ماتریس مشابه تولید میکنند:>> a=[1 2;3 4]a = 1 2 3 4>> a=[1 23 4]a = 1 2 3 4ماتریسها میتوانند شامل عبارات جبری و انتسابی نیز باشند.>> b=[a(1,1) 1+6]b = 1 7>> c=[b a(1,:)]c = 1 7 1 2برای ترانهاده(ستونی) کردن ماتریسها کافیست در انتهای ماتریس علامت " ' " (کوتیشن) را بگذاریم.هر دو ماتریس ذیل باهم برابرند:>> a=[1 2 3]'a = 1 2 3>> a=[1;2;3]a = 1 2 3ماتریسها را در داخل یکدیگر نیز میتوان جای داد و همزمان عملیات جبری انجام داد:>> f=[1 2 3 4]f = 1 2 3 4>> g=[f' f']g = 1 1 2 2 3 3 4 4>> h=[2*f]h = 2 4 6 8>> h=[2*f']h = 2 4 6 8 مثال های زیر را با دقت تحلیل کنید:>> c=rand(4,4)c = 0.6555 0.2769 0.6948 0.4387 0.1712 0.0462 0.3171 0.3816 0.7060 0.0971 0.9502 0.7655 0.0318 0.8235 0.0344 0.7952>> c([1,2],[2,3])ans = 0.2769 0.6948 0.0462 0.3171>> c([1,2],[1,2])ans = 0.6555 0.2769 0.1712 0.0462>> c([1,3],[1,2])ans = 0.6555 0.2769 0.7060 0.0971>> c([1,2],[1,3])ans = 0.6555 0.6948 0.1712 0.3171>> c([2:4],[1:3])ans = 0.1712 0.0462 0.3171 0.7060 0.0971 0.9502 0.0318 0.8235 0.0344>> c([2,4],[1,3])ans = 0.1712 0.3171 0.0318 0.0344>> c([1,end],[1,end])ans = 0.6555 0.4387 0.0318 0.7952>> c([1:end],[1:end])ans = 0.6555 0.2769 0.6948 0.4387 0.1712 0.0462 0.3171 0.3816 ...
ماتریس (MATRIX)

هر آنچه در مورد ماتریسها می خواهید بدانید به طور خلاصه گردآوری شده: دانلود انواع ماتریس،جمع و ضرب ماتریس،Hadamard product،Frobenius inner product،ترانهاده،وارون ماتریس،پادمتقارن ،نگاشت ، دترمینان ،روش بسط لاپلاس دترمینان ، ماتریس همسازه و الحاقی ، روش ساروس ، فرمول لایبنیز براي محاسبه دترمینان ، وارون ماتریس ، اثر ماتریس ،خواص دترمینان ، ماتریس متعامد، ماتریس یکانی ، رنک ماتریس ،بردارویژه ، ماتریس هرمیتی ، ماتریس نمایی ، ماتریسهاي قطري شونده ، ماتریس مثبت معین
معکوس ماتریس 3 * 3 و بالاتر ( n * n )
در طی پست های قبل با نحوه به دست آوردن دترمینان یک ماتریس، ماتریس کهاد، ماتریس همسازه و ماتریس الحاقی آشنا شدیم و حالا نوبت رسیده است تا معکوس یا واران یک ماتریس را محاسبه کنیم. پیش شرط : همه می دانید که اولا ماتریس شما باید یک ماتریس مربعی باشد و دوما دترمینان آن مخالف صفر 0 باشد. اگر این دو شرط را رعایت کنید ماتریس شما واران پذیر خواهد بود.محاسبه :اگر اطلاعاتی در مورد دترمینان و ماتریس الحاقی ندارید می توانید از لینک های ابتدای پست استفاده کنید یا در اینترنت در مورد آنها جست و جو کنید چون دیگر در این پست در مورد انها صحبت نمی کنیم. فرمول زیر برای محاسبه دترمینان به کار میرود.Inv (matrix) = 1 / Det(matrix) x Adjugate-matrixInv (matrix) : ماتریس معکوسDet (matrix) : دترمینان ماتریسAdjugate-matrix : ماتریس الحاقیبه همین راحتی. پس معکوس ماتریس از ضرب عدد ( 1 تقسیم بر دترمینان ماتریس) در ماتریس الحاقی یا به عبارت دیگر از ضرب معکوس دترمینان ماتریس در ماتریس الحاقی به دست می آید. و واضح است که چون دترمینان در مخرج نشسته است، هیچگاه نمیتواند مقدار صفر داشته باشد. توضیح بیشتر همراه با مثال در مورد ماتریس 3 در 3
انواع ماتریسها
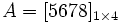
ماتریس مربعی ماتریسی است که تعداد سطرها و ستونهای آن با هم برابر باشد. ماتریس سطری ماتریسی است که یک سطر دارد. مثلا ماتریس ستونی ماتریسی است که یک ستون دارد. مثلا ماتریس ماتریسی است که فقط یک عضو دارد. مثلا ماتریس صفر تمام عضوهای آن ماتریس برابر صفر میباشد. این ماتریس در جمع ماتریسها حکم عدد صفر را در جمع اعداد حقیقی دارد یعنی عضو خنثی است. ماتریس واحد یا یکه ماتریسی است مربعی که عضوهای قطر اصلی آن همگی برابر با یک و بقیه عضوهای آن برابر صفر میباشد. این ماتریس را با I نشان میدهند. مثلا !ماتریس قرینه اگر ماتریسی را در عدد 1- ضرب کنیم قرینه آن ماتریس بدست میآید. بعبارت دیگر قرینه یک ماتریس ، ماتریسی است که عضوهای آن قرینه عضوهای ماتریس اصلی باشند. ماتریس قطری ماتریسی است مربعی که قطر اصلی آن اعداد حقیقی بوده و سایر عضوهای آن برابر صفر باشد. مثلا ماتریس عددی یا اسکالر ماتریسی است قطری که عضوهای قطر اصلی آن برابر باشند. مثلا ماتریس منفرد ماتریسی است مربعی که دترمینان آن برابر صفر باشد. یعنی ماتریس غیرمنفرد یا وارونپذیر اگر در یک ماتریس مربعی دترمینان آن صفر نباشد به آن ماتریس غیرمنفرد میگویند. یعنی ماتریس معکوس یا ماتریس وارون ماتریس مربعی A را در نظر میگیریم اگر ماتریسی مانند B پیدا شود بطوریکه داشته باشیم AB=BA=I به ماتریس B وارون یا معکوس ماتریس A میگویند معمولا ماتریس معکوس A را بصورت نشان میدهند و در نتیجه داریم: ماتریس همسازه اگر در یک ماتریس مربعی به جای هر عضو ، کوفاکتور آن را قرار دهیم ماتریسی بدست میآید که به آن همسازه میگویند. ماتریس همسازه A را با N نمایش میدهند.برای هر در ماتریس ، همسازه برابر است با عدد کوفاکتور عضو بطوریکه ، را دترمینان ماتریس حاصل از حذف سطر i ام و ستون j ام ماتریس A میتوان تعریف کرد. ماتریس وابسته یا الحاقی به ترانسپوزه ماتریس همسازه A ماتریس وابسته A میگویند و آن را با نشان میدهند. ماتریس متقارن اگر ترانسپوزه یک ماتریس با آن ماتریس برابر باشد آن ماتریس را متقارن مینامند بعبارت دیگر ماتریس A متقارن است در صورتیکه باشد. اگر در ماتریس جای سطرها و ستونها را عوض کنیم و ماتریس تغییر نکند به آن متقارن میگویند. ماتریس ضدمتقارن یا آنتیمتقارن هرگاه قرینه ترانسپوزه ماتریس A برابر A شود، به آن ماتریس ضدمتقارن میگویند و داریم ماتریس پایین مثلثی اگر در یک ماتریس مربعی تمام عضوهای بالای قطر اصلی صفر باشند به آن ماتریس پایین مثلثی میگویند یعنی ماتریس بالا مثلثی اگر در یک ماتریس مربعی تمام عضوهای پایین قطر اصلی صفر باشند به ...
