آموزش انتگرال
آموزش کامل انتگرال
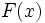
انتگرال نامعین اگر پاد مشتق باشد ، آنگاه به ازای هر مقدار ثابت یک پاد مشتق است.زیرا اگر آنگاه: نکته اگر جوابی برای باشد ، فرمول همه جوابها را به دست میدهد. انتگرال نامعین مجموعه همه پاد مشتقهای یک تابع چون را انتگرال نامعین نسبت به مینامند و با نشان میدهند. هرگاه فرمول همه پادمشتقهای را به دست دهد، آنرا چنین مشخص میکنیم : تابع را انتگرال ده انتگرال و را ثابت انتگرالگیری مینامیم. همچنین نشان میدهد که متغیر انتگرالگیری است. خواص انتگرال انتگرال مشتق یک تابع مشتقپذیر برابر است با به علاوه یک ثابت دلخواه. یک ثابت را میتوان از زیر نماد انتگرالگیری بیرون آورد.(توجه شود که عباراتی را که توابعی از متغیر انتگرالگیری اند ، نمیتوان از زیر نماد انتگرالگیری بیرون آورد.) انتگرال مجموع دو تابع برابر مجموع انتگرالهای آنهاست.این مطلب را میتوان به مجموع هر تعداد متناهی از توابع تعمیم داد. فرمول های انتگرال گیری , , , , در این دستورها یا متغیر مستقل است و یا تابعی مشتقپذیر از متغیر مستقل دیگری است. اگر آنگاه انتخاب مقدار ثابت انتگرالگیری در حل یک معادله دیفرانسیل مانند معمولا به دنبال جواب خاصی هستیم که شرایط عددی از پیش تعیین شده را برآورده سازد.بدین منظور نخست جواب عمومی را تعیین میکنیم که همه جوابهای ممکن را به دست میدهد . سپس مقداری از را تعیین میکنیم که جواب خاص مطلوب را به دست دهد. اگر نقطهای چون از دامنه را در نظر بگیریم و مقدار دلخواه را برگزینیم ، میتوان با قرار دادن و در معادله و حل آن نسبت به جوابی را یافت که از نقطه بگذرد.به این ترتیب داریم یا . خم خمی است که از میگذرد. انتگرالگیری به کمک تغییر متغیر در حل انتگرالها با روش تغییر متغیر ، به جای تابع پیوسته و مشتق پذیر را قرار می دهیم، یعنی : بعد از حل ، بر اساس تابع معکوس ، به جای نسبت به قرار میدهیم . یعنی: از فرمول فوق به صورت زیر هم میتوان استفاده کرد: انتگرالگیری به روش جزء به جزء دستور موسوم به انتگرالگیری به روش جزء به جزء است که در آن توابعی مشتقپذیر از هستند. اگر انتگرال به صورت حاصلضرب یک تابع لگاریتمی یا یک تابع معکوس مثلثاتی ، در یک چند جمله ای باشد، در این صورت معمولا را تابع لگاریتمی یا تابع معکوس مثلثاتی انتخاب میکنند ولی اگر انتگرال حاصلضرب یک تابع لگاریتمی یا یک تابع نمایی در یک تابع جبری باشد ، معمولا تابع جبری را فرض میکنند. دید کلی برای آنکه بتوانیم مساحت شکل مسطح را حساب کنیم واحدی برای مساحت در نظر میگیریم که عبارت است ...
آموزش کامل انتگرال
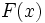
انتگرال نامعین اگر پاد مشتق باشد ، آنگاه به ازای هر مقدار ثابت یک پاد مشتق است.زیرا اگر آنگاه: نکته اگر جوابی برای باشد ، فرمول همه جوابها را به دست میدهد. انتگرال نامعین مجموعه همه پاد مشتقهای یک تابع چون را انتگرال نامعین نسبت به مینامند و با نشان میدهند. هرگاه فرمول همه پادمشتقهای را به دست دهد، آنرا چنین مشخص میکنیم : تابع را انتگرال ده انتگرال و را ثابت انتگرالگیری مینامیم. همچنین نشان میدهد که متغیر انتگرالگیری است. خواص انتگرال انتگرال مشتق یک تابع مشتقپذیر برابر است با به علاوه یک ثابت دلخواه. یک ثابت را میتوان از زیر نماد انتگرالگیری بیرون آورد.(توجه شود که عباراتی را که توابعی از متغیر انتگرالگیری اند ، نمیتوان از زیر نماد انتگرالگیری بیرون آورد.) انتگرال مجموع دو تابع برابر مجموع انتگرالهای آنهاست.این مطلب را میتوان به مجموع هر تعداد متناهی از توابع تعمیم داد. فرمول های انتگرال گیری , , , , در این دستورها یا متغیر مستقل است و یا تابعی مشتقپذیر از متغیر مستقل دیگری است. اگر آنگاه انتخاب مقدار ثابت انتگرالگیری در حل یک معادله دیفرانسیل مانند معمولا به دنبال جواب خاصی هستیم که شرایط عددی از پیش تعیین شده را برآورده سازد.بدین منظور نخست جواب عمومی را تعیین میکنیم که همه جوابهای ممکن را به دست میدهد . سپس مقداری از را تعیین میکنیم که جواب خاص مطلوب را به دست دهد. اگر نقطهای چون از دامنه را در نظر بگیریم و مقدار دلخواه را برگزینیم ، میتوان با قرار دادن و در معادله و حل آن نسبت به جوابی را یافت که از نقطه بگذرد.به این ترتیب داریم یا . خم خمی است که از میگذرد. انتگرالگیری به کمک تغییر متغیر در حل انتگرالها با روش تغییر متغیر ، به جای تابع پیوسته و مشتق پذیر را قرار می دهیم، یعنی : بعد از حل ، بر اساس تابع معکوس ، به جای نسبت به قرار میدهیم . یعنی: از فرمول فوق به صورت زیر هم میتوان استفاده کرد: انتگرالگیری به روش جزء به جزء دستور موسوم به انتگرالگیری به روش جزء به جزء است که در آن توابعی مشتقپذیر از هستند. اگر انتگرال به صورت حاصلضرب یک تابع لگاریتمی یا یک تابع معکوس مثلثاتی ، در یک چند جمله ای باشد، در این صورت معمولا را تابع لگاریتمی یا تابع معکوس مثلثاتی انتخاب میکنند ولی اگر انتگرال حاصلضرب یک تابع لگاریتمی یا یک تابع نمایی در یک تابع جبری باشد ، معمولا تابع جبری را فرض میکنند. دید کلی برای آنکه بتوانیم مساحت شکل مسطح را حساب کنیم واحدی برای مساحت در نظر میگیریم که عبارت است از مساحت ...
آموزش انتگرال
آموزش انتگرال انتگرالها يک بحث اساسي رياضيات عالي را تشکيل داده که ميتوان کاربرد آنرا درتمام علوم طبيعي، انساني وغيره مورد مطالعه قرارداد. اولين بار لايب نيتس نماد استانداردي براي انتگرال معرفي کرد. aو b نقاط ابتدا و انتهاي بازه هستند و f تابعي انتگرالپذير است و dx نمادي براي متغير انتگرال گيري است. از لحاظ تاريخي dx يک کميت بي نهايت کوچک را نشان ميدهد. هر چند در تئوريهاي جديد، انتگرال گيري بر پايه متفاوتي پايه گذاري شده است. تابع اوليه هر گاه معادله مشتق تابعي معلوم باشد وبخواهيم معادله اصلي تابع را تعيين کنيم اين عمل را تابع اوليه مي ناميم. تعريف: تابع اوليه y = f(x)را تابعي مانند Y = F(x) + c مي ناميم،هرگاه داشته باشيم: cعدد ثابت (y = F(x) + c)' = y = f(x) انتگرال نامعين تعريف:هرگاه معادله ديفرانسيلي تابعي معلوم باشد وبخواهيم معادله اصلي تابع را معلوم کنيم اين عمل راانتگرال نا معيين ناميده و آن را با نماد نمايش مي دهند. بنا به تعريف نماد را انتگرال نامعين ناميده وحاصل آن را تابعي مانندF(x) + c در نظر ميگيريم هر گاه داشته باشيم: با شرط: (F(x) + c)' = f(x) انتگرال معين بنا به تعريف نماد را انتگرال معين ناميده و حاصل آن را عددي به صورت زير تعريف ميکنيم: aaوb را به ترتيب کرانهاي بالا و پايين انتگرال ميناميم. تابع انتگرالپذير اگر تابعي داراي انتگرال باشد به آن انتگرالپذير گويند. تعبير هندسي انتگرال از نظر هندسي انتگرال برابر است با مساحت سطح محصور زير نمودار. نکته! انتگرال نمودار سه بعدي(انتگرال سه گانه)معرف حجم محصور زير نمودار است. انتگرال يک تابع مثبت پيوسته در بازه (0,10) در واقع پيدا کردن مساحت محصور بين خطوط x=0 , x=10 و خم منحني fx است. aو b نقاط ابتدا و انتهاي بازه هستند و f تابعي انتگرالپذير است و dx نمادي براي متغير انتگرال گيري است. انتگرال يک تابع مساحت زير نمودار آن تابع است. انتگرال گيري انتگرال گيري به معني محاسبه سطح زير نمودار با استفاده از روشها وقوانين انتگرال گيري است. 1.f تابعي در بازه (a,b) در نظر ميگيريم. 2.پاد مشتق f را پيدا ميکنيم که تابعي است مانند f که و داريم: 3.قضيه اساسي حساب ديفرانسيل و انتگرال را در نظر ميگيريم: بنابراين مقدار انتگرال ما برابر خواهد بود. به اين نکته توجه کنيد که انتگرال واقعاً پاد مشتق نيست (يک عدد است) اما قضيه اساسي به ما اجازه ميدهد تا از پاد مشتق براي محاسبه مقدار انتگرال استفاده کنيم. معمولاً پيدا کردن پاد مشتق تابع f کار سادهاي نيست و نياز به استفاده از تکنيکهاي انتگرالگيري دارد اين تکنيکها عبارتاند از : انتگرال گيري بهوسيله تغيير متغير انتگرال گيري جزء به جزء : ...
آموزش انتگرال
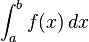
نتگرالها يک بحث اساسي رياضيات عالي را تشکيل داده که ميتوان کاربرد آنرا درتمام علوم طبيعي، انساني وغيره مورد مطالعه قرارداد.اولين بار لايب نيتس نماد استانداردي براي انتگرال معرفي کرد. aو b نقاط ابتدا و انتهاي بازه هستند و f تابعي انتگرالپذير است و dx نمادي براي متغير انتگرال گيري است. از لحاظ تاريخي dx يک کميت بي نهايت کوچک را نشان ميدهد. هر چند در تئوريهاي جديد، انتگرال گيري بر پايه متفاوتي پايه گذاري شده است. تابع اوليه هر گاه معادله مشتق تابعي معلوم باشد وبخواهيم معادله اصلي تابع را تعيين کنيم اين عمل را تابع اوليه مي ناميم. تعريف: تابع اوليه y = f(x)را تابعي مانند Y = F(x) + c مي ناميم،هرگاه داشته باشيم: cعدد ثابت (y = F(x) + c)' = y = f(x) انتگرال نامعين تعريف:هرگاه معادله ديفرانسيلي تابعي معلوم باشد وبخواهيم معادله اصلي تابع را معلوم کنيم اين عمل راانتگرال نا معيين ناميده و آن را با نماد نمايش مي دهند. بنا به تعريف نماد را انتگرال نامعين ناميده وحاصل آن را تابعي مانندF(x) + c در نظر ميگيريم هر گاه داشته باشيم: با شرط: (F(x) + c)' = f(x) انتگرال معين بنا به تعريف نماد را انتگرال معين ناميده و حاصل آن را عددي به صورت زير تعريف ميکنيم: a aوb را به ترتيب کرانهاي بالا و پايين انتگرال ميناميم. تابع انتگرالپذير اگر تابعي داراي انتگرال باشد به آن انتگرالپذير گويند. تعبير هندسي انتگرال از نظر هندسي انتگرال برابر است با مساحت سطح محصور زير نمودار. نکته! انتگرال نمودار سه بعدي(انتگرال سه گانه)معرف حجم محصور زير نمودار است. انتگرال يک تابع مثبت پيوسته در بازه (0,10) در واقع پيدا کردن مساحت محصور بين خطوط x=0 , x=10 و خم منحني fx است. aو b نقاط ابتدا و انتهاي بازه هستند و f تابعي انتگرالپذير است و dx نمادي براي متغير انتگرال گيري است. انتگرال يک تابع مساحت زير نمودار آن تابع است. انتگرال گيري انتگرال گيري به معني محاسبه سطح زير نمودار با استفاده از روشها وقوانين انتگرال گيري است. 1.f تابعي در بازه (a,b) در نظر ميگيريم. 2.پاد مشتق f را پيدا ميکنيم که تابعي است مانند f که و داريم: 3.قضيه اساسي حساب ديفرانسيل و انتگرال را در نظر ميگيريم: بنابراين مقدار انتگرال ما برابر خواهد بود. به اين نکته توجه کنيد که انتگرال واقعاً پاد مشتق نيست (يک عدد است) اما قضيه اساسي به ما اجازه ميدهد تا از پاد مشتق براي محاسبه مقدار انتگرال استفاده کنيم. معمولاً پيدا کردن پاد مشتق تابع f کار سادهاي نيست و نياز به استفاده از تکنيکهاي انتگرالگيري دارد اين تکنيکها عبارتاند از : انتگرال گيري بهوسيله تغيير متغير انتگرال گيري جزء به جزء : انتگرال ...
آموزش انتگرال به همراه فرمولهای انتگرال
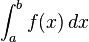
انتگرالها يک بحث اساسي رياضيات عالي را تشکيل داده که ميتوان کاربرد آنرا درتمام علوم طبيعي، انساني وغيره مورد مطالعه قرارداد. اولين بار لايب نيتس نماد استانداردي براي انتگرال معرفي کرد. aو b نقاط ابتدا و انتهاي بازه هستند و f تابعي انتگرالپذير است و dx نمادي براي متغير انتگرال گيري است. از لحاظ تاريخي dx يک کميت بي نهايت کوچک را نشان ميدهد. هر چند در تئوريهاي جديد، انتگرال گيري بر پايه متفاوتي پايه گذاري شده است. تابع اوليه هر گاه معادله مشتق تابعي معلوم باشد وبخواهيم معادله اصلي تابع را تعيين کنيم اين عمل را تابع اوليه مي ناميم. تعريف: تابع اوليه y = f(x)را تابعي مانند Y = F(x) + c مي ناميم،هرگاه داشته باشيم: cعدد ثابت (y = F(x) + c)' = y = f(x) انتگرال نامعين تعريف:هرگاه معادله ديفرانسيلي تابعي معلوم باشد وبخواهيم معادله اصلي تابع را معلوم کنيم اين عمل راانتگرال نا معيين ناميده و آن را با نماد نمايش مي دهند. بنا به تعريف نماد را انتگرال نامعين ناميده وحاصل آن را تابعي مانندF(x) + c در نظر ميگيريم هر گاه داشته باشيم: با شرط: (F(x) + c)' = f(x) انتگرال معين بنا به تعريف نماد را انتگرال معين ناميده و حاصل آن را عددي به صورت زير تعريف ميکنيم: a aوb را به ترتيب کرانهاي بالا و پايين انتگرال ميناميم. تابع انتگرالپذير اگر تابعي داراي انتگرال باشد به آن انتگرالپذير گويند. تعبير هندسي انتگرال از نظر هندسي انتگرال برابر است با مساحت سطح محصور زير نمودار. نکته! انتگرال نمودار سه بعدي(انتگرال سه گانه)معرف حجم محصور زير نمودار است. انتگرال يک تابع مثبت پيوسته در بازه (0,10) در واقع پيدا کردن مساحت محصور بين خطوط x=0 , x=10 و خم منحني fx است. aو b نقاط ابتدا و انتهاي بازه هستند و f تابعي انتگرالپذير است و dx نمادي براي متغير انتگرال گيري است. انتگرال يک تابع مساحت زير نمودار آن تابع است. انتگرال گيري انتگرال گيري به معني محاسبه سطح زير نمودار با استفاده از روشها وقوانين انتگرال گيري است. 1.f تابعي در بازه (a,b) در نظر ميگيريم. 2.پاد مشتق f را پيدا ميکنيم که تابعي است مانند f که و داريم: 3.قضيه اساسي حساب ديفرانسيل و انتگرال را در نظر ميگيريم: بنابراين مقدار انتگرال ما برابر خواهد بود. به اين نکته توجه کنيد که انتگرال واقعاً پاد مشتق نيست (يک عدد است) اما قضيه اساسي به ما اجازه ميدهد تا از پاد مشتق براي محاسبه مقدار انتگرال استفاده کنيم. معمولاً پيدا کردن پاد مشتق تابع f کار سادهاي نيست و نياز به استفاده از تکنيکهاي انتگرالگيري دارد اين تکنيکها عبارتاند از : انتگرال گيري بهوسيله تغيير متغير انتگرال گيري جزء به جزء : انتگرال گيري ...
آموزش انتگرالها
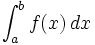
در حساب دیفرانسیل و انتگرال ، از انتگرال یک تابع برای عمومیت دادن به محاسبه مساحت ، حجم ، جرم یک تابع استفاده می شود. فرایند پیدا کردن جواب انتگرال را انتگرال گیری گویند.البته تعاریف متعددی برای انتگرال گیری وجود دارد ولی در هر حال جواب مشابه ای از این تعاریف بدست می آید. انتگرال یک تابع مثبت پیوسته در بازه (a,b) در واقع پیدا کردن مساحت بین خطوط x=0 , x=10 و خم منفی F است . پس انتگرال F بین a و b در واقع مساحت زیر نمودار است. اولین بار لایب نیتس نماد استانداری برای انتگرال معرفی کرد و به عنوان مثال انتگرال f بین a و b رابه صورت نشان می دهند علامت ،انتگرال گیری از تابع f را نشان می دهند ،aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرال پذیر است و dx نمادی برای متغیر انتگرال گیری است. انتگرال یک تابع مساحت زیر نمودار آن تابع است. از لحاظ تاریخی dx یک کمیت بی نهایت کوچک را نشان می دهد. هر چند در تئوریهای جدید، انتگرال گیری بر پایه متفاوتی پایه گذاری شده است به عنوان مثال تابع f را بین x=0 تا x=10 در نظر بگیرید ،مساحت زیر نمودار در واقع مساحت مستطیل خواهدبود که بین x=0 ،x=10 ،y=0 ،y=3 محصور شده است یعنی دارای طول 10 و عرض 3است پس مساحت آن برابر 30 خواهد بود . اگر تابعی دارای انتگرال باشد به آن انتگرال پذیر گویند و تابعی که از انتگرال گیری از یک تابع حاصل می شود تابع اولیه گویند . اگر انتگرال گیری از تابع در یک محدوده خاص باشند به آن انتگرال معین گویند که نتیجه آن یک عدد است ولی اگر محدوده آن مشخص نباشد به آن انتگرال نامعین گویند. محاسبه انتگرال اکثر روش های اساسی حل انتگرال بر پایه قضیه اساسی حساب دیفرانسیل و انتگرال بنا نهاده شده است که بر طبق آن داریم: 1.f تابعی در بازه (a,b) در نظر می گیریم . 2.پاد مشتق f را پیدا می کنیم که تابعی است مانند f که و داریم: 3.قضیه اساسی حساب دیفرانسیل و انتگرال را در نظر می گیریم: بنابراین مقدار انتگرال ما برابر خواهد بود. به این نکته توجه کنید که انتگرال واقعاً پاد مشتق نیست (یک عدد است) اما قضیه اساسی به ما اجازه می دهد تا از پاد مشتق برای محاسبه مقدار انتگرال استفاده کنیم . معمولاً پیدا کردن پاد مشتق تابع f کار ساده ای نیست و نیاز به استفاده از تکنیکهای انتگرالگیری دارد این تکنیکها عبارتند از : انتگرال گیری بوسیله تغییر متغیر انتگرال گیری جزء به جزء انتگرال گیری با تغییر متغیر مثلثاتی انتگرال گیری بوسیله تجزیه کسرها روش هایی دیگر نیز وجود دارد که برای محاسبه انتگرالهای معین به کار می رود همچنین می توان بعضی از انتگرال ها با ترفند هایی حل کرد برای مثال می توانید به انتگرال گاوسی مراجعه کنید . تقریب انتگرالهای ...
دانلود جزوه اموزش مقدماتی انتگرال

دانلود جزوه اموزش مقدماتی انتگرال,spowpowerplant, Blog,مهندسی مکانیک,وبلاگ یک مهندس,اسپاو, Weblog,همه چیز درباره نیروگاه,مهندسی مکانیک,برق و الکترونیک,پمپ پایپینگ توربین,مهندسی شیمی,تحقیق,داستان کوتاه,دانلود کتاب جزوه مقاله پروژه,پروژه تحقیق پایان نامه,مهندسی,Engineer,مدیریت,دانلود کتابهای مهندسی,معرفی و نقد فیلم و کتاب,دانلود جزوه,دانلود مقاله,توربین,نیروگاه,spow, Persian,Iran, Iranian,Google,Yahoo,MSN, Weblogs, Blogs"> وبلاگ یک مهندس... - دانلود جزوه اموزش مقدماتی انتگرالوبلاگ یک مهندس... دانلود جزوه اموزش مقدماتی انتگرال دانلود جزوه اموزش مقدماتی انتگرالاشنایی با مفهوم انتگرال وروشهای انتگرال گیریجزوه اموزشی انتگرال را ازلینک زیر دریافت کنیددانلود جزوهپسورد : spow--------------------------------برای دانلود مجموعه جزوات اموزشی بحث انتگرال (6 جزوه) به لینک زیر مراجعه فرمایید:دانلود جزوه انتگرال
انتگرالگیری به روش جز به جز

روش انتگرالگیری جز به جز (Integration by Parts) روشی است که به وسیلهی آن میتوان بسیاری از انتگرالهایی را که با استفاده از فرمولهای رایج قابل حل نیستند، حساب کرد. این روش خصوصا در مواقعی کاربردی است که تابعی که میخواهیم از آن انتگرال بگیریم، حاصلضرب یک تابع جبری و یک تابع مثلثاتی، یا حاصلضرب یک تابع جبری و یک تابع لگاریتمی باشد مانند نمونههای زیر: فرمول روش جز به جز به این صورت است: اگر توابع u و v نسبت به x مشتقپذیر باشند، آنگاه: اثبات: این فرمول با استفاده از قانون «مشتق حاصلضرب» بدست میآید: اگر این فرمول را بازآرایی کنیم داریم: که با انتگرالگیری از آن نسبت به x فرمول انتگرالگیری جز به جز حاصل خواهد شد. اساس کار این فرمول آن است که یک انتگرال داده شده را به انتگرال دیگری تبدیل میکند. اگر u و dv مناسب اختیار شوند، انتگرال جدید ممکن است سادهتر از انتگرال اول باشد. با توجه به اینکه انتخاب u و dv بسیار مهم است، هنگام انتخاب آنها توصیههای زیر میتواند به انتخاب سریعتر و بهتر کمک کند: dv را معمولا باید بخش پیچیدهتر تابع مورد انتگرالگیری که به وسیلهی فرمولهای اساسی انتگرال قابل محاسبه باشد، در نظر گرفت. u را بخشی از تابع مورد انتگرال در نظر میگیرند که مشتقش سادهتر از v است.مثال: حل: و و تذکر: هنگام محاسبه انتگرال به روش جز به جز، u و dv باید به گونهای انتخاب شوند که انتگرال جدید سادهتر از انتگرال اصلی باشد. برای نمونه اگر فرض میکردیم که: و آنگاه: و و روش جز به جز به انتگرال زیر منتهی میشد: و مشاهده میشود که با این کار انتگرال جدید عملا پیچیدهتر از انتگرال اصلی است. ارائهی یک روش ساده برای انتخاب u و v عملا کاری بسیار مشکل است، با وجود این دستورالعملهای کلیای وجود دارند؛ مثلا: «اگر در انتگرال اصلی وجود داشت، نباید dv را گرفت»، زیرا در این صورت توان x پس از اعمال روش جز به جز، بیشتر میشود و انتگرال به دست آمده مشکلتر از قبلی خواهد بود. تذکر: گاهی برای حل یک انتگرال لازم میشود چندین بار از روش جز به جز استفاده کنیم. مثال: که لازم است برای جملهی دوم، همانند مثال قبل، از روش جز به جز استفاده شود. در پایین این صفحه چند مثال دیگر به روش جز به جز حل شده است (زبان انگلیسی)، روی لینک answer کلیک کنید تا جوابها را مشاهده نمایید. در این سایت همچنین میتوانید به صورت آن لاین به جواب انتگرال های مورد نظرتان دست یابید.
آموزش تصویری و ساده انتگرال ویژه دبیرستانیها
آموزش انتگرال توسط آقای مجید وجدانی درستکار آموزش ساده انتگرال _ قسمت اول آموزش ساده انتگرال _ قسمت دوم
