پنج ضلعی
چند ضلعی

پنج ضلعی منتظم: نوار بلند کاغذی آماده کنید که عرض یکسان داشته باشد. برای ساخت یک پنج ضلعی منتظم با این نوار به تر تیب زیر عمل کنید: ۱٫ دو سر نوار را بگیرید و با آن یک گره ساده بزنید مانند شکل زیر: ۲٫ گره را به آرامی سفت کنید و رد های کاغذ را صاف کنید. ۳٫ نوار های اضافی را ببرید ،پنج ضلعی منتظم بوجود می آید. ۴٫ گره را باز کنید و ذوزنقه های تشکیل شده را با هم بررسی و مقایسه کنید. هفت ضلعی منتظم: نوار بلند کاغذی آماده کنید که عرض یکسان داشته باشد. برای ساخت یک هفت ضلعی منتظم با این نوار به ترتیب زیر عمل کنید: ۱٫ دو سر نوار را بگیرید و با آن یک گره ساده بزنید. (مانند پنج ضلعی منتظم) ۲٫گره را سفت نکنید و وسط گره (ناحیه ی ۱) را در نظر داشته باشید. ۳٫ مجددأ یک سر نوار را به قصد زدن گره دوم زیر سر دیگر برده ،و از ناحیه ۱ (وسط گره اول) عبور دهید. ۴٫گره را به آرامی سفت کنید و رد های کاغذ را صاف کنید. ۵٫نوار های اضافی را ببرید ،هفت ضلعی منتظم بوجود می آید.
روش رسم پنج ضلعی منتظم
ابتدا خط دلخواهی رسم کنید و با مشخص کردن دو نقطه الف و ب پاره خطی به طول 5 جدا نمایید. وسط پاره خط ((الف ب)) را بیابید و آن را نقطه ((ج)) بنامید. ضمناً از نقطه ب عمودی به اندازه طول ((الف ب)) اخراج کنید و این نقطه را ((د)) نامگذاری کنید. حالا پرگار را روی نقطه ((ج)) گذاشته کمانی به شعاع ((الف ب)) رسم کنید تا نقطه ((ه)) را روی خط مشخص کند: دهانه پرگار را به اندازه ((الف ه)) باز کنید و به مرکزیت ((الف)) و ((ب)) دو قوس بزنید تا همدیگر را در ((و)) قطع کنند. از ((الف)) و ((ب)) به ((و)) وصل کنید. به یک مثلث رسیده ایم که پایه رسم بسیاری از شکل هاست: پرگار را به اندازه ((الف ب)) باز کنید و به مرکزیت ((الف)) و ((ب)) دو کمان رسم کنید تا نقاط ((ز)) و ((ح)) پدیدار شوند. پنج نقطه را به هم وصل نمایید: پنج ضلعی منتظم آماده شده است! ماخذ:www.ajayeb.ir/iranianmath/index.php
چند ضلعی های منتظم
در هندسه اقلیدسی، یک چندضلعی منتظم، چندضلعی است که همه زوایا واضلاع آن هماندازهاند. چندضلعیهای منتظم، میتوانند کوژ و یا به شکل ستاره باشند. در حالت حدی، یک دنباله از چندضلعیهای منتظم با افزایش تعداد اضلاع، در صورت ثابت ماندن محیط بهدایره تبدیل میشود و در صورت ثابت ماندن طول ضلع، به apeirogon تبدیل میشود. محتویات [نهفتن] ۱ ویژگیها ۲ چندضلعیهای منتظم کوژ ۲.۱ زاویهها ۲.۲ قطرها ۲.۳ مساحت ۳ چندضلعیهای منتظم ستارهای ۴ جستارهای وابسته ۵ پانویس ویژگیها[ویرایش] ویژگیهای بیانشده در ادامه، برای همهٔ چندضلعیهای منتظم (اعم از کوژ وستارهای) برقرار است. یک چندضلعی منتظم n-ضلعی، تقارن چرخشی از مرتبهٔ n دارد. همهٔ رأسهای یک چندضلعی منتظم بر روی یک دایره (دایره محیطی) قرار میگیرند. بهعبارت دیگر، رأسها نقاطی همدایره هستند. یعنی یک چندضلعی منتظم، لزوماً یک چندضلعی دایرهای هم هست. هر چندضلعی منتظم، یک دایره محاطی دارد که به همه اضلاع در نقطهٔ وسط آنهامماس است. بنابراین هر چندضلعی منتظم، لزوماً یک چندضلعی مماسی هم هست. یک n-ضلعی منتظم با استفاده از خطکش و پرگار قابل ترسیم است؛ اگر و تنها اگر فاکتورهای اول فرد n، اعداد اول فرمای متفاوتی باشند. چندضلعیهای منتظم کوژ[ویرایش] همهٔ چندضلعیهای سادهٔ منتظم، کوژ هستند. چندضلعیهای منتظم باتعداد اضلاع یکسان، متشابه هستند. یک n-ضلعی منتظم کوژ، بانماد شلفلی {n} نشان داده میشود. مثلثمتساویالاضلاع{۳} مربع{۴} پنجضلعی{۵} ششضلعی{۶} هفتضلعی{۷} هشتضلعی{۸} نهضلعی{۹} دهضلعی{۱۰} یازدهضلعی{۱۱} دوازدهضلعی{۱۲} سیزدهضلعی{۱۳} چهاردهضلعی{۱۴} پانزدهضلعی{۱۵} شانزدهضلعی{۱۶} هفدهضلعی{۱۷} هجدهضلعی{۱۸} نوزدهضلعی{۱۹} بیستضلعی{۲۰} سیضلعی{۳۰} چهلضلعی{۴۰} پنجاهضلعی{۵۰} شصتضلعی{۶۰} هفتادضلعی{۷۰} هشتادضلعی{۸۰} نودضلعی{۹۰} صدضلعی{۱۰۰} زاویهها[ویرایش] برای یک n-ضلعی منتظم کوژ، اندازهٔ هر زاویهٔ داخلی برابر است با: یا درجهیا رادیان و اندازهٔ هر زاویه خارجی آن برابر است با درجه. قطرها[ویرایش] برای n > ۲، تعداد قطرهای n-ضلعی، برابر است با ، بهعنوان مثال برای مثلث، چهارضلعی، پنجضلعی و ششضلعی، تعداد قطرها بهترتیب، ۰، ۲، ۵ و ۹ است. برای یک n-ضلعی منتظم محاطشده در یک دایره به شعاع واحد، حاصلضرب فاصلهٔ هر رأس تا همهٔ رأسهای دیگر، برابر است با n. مساحت[ویرایش] پنجضلعی منتظم با طول ضلع s، شعاعدایره محیطی r و شعاع دایره محاطی a مساحت یک n-ضلعی منتظم کوژ با اندازهٔ ضلع s، شعاع دایره ...
پنتاگرام یا پنج ضلعی وارونه چیست ؟
در فرهنگ و تمدن باستان مایان های امریکای لاتین، هند، چین، مصرو یونان از مهمترین و پرمعناترین علامتها بوده است. ابتدایی ترین شکل پنتاگرام بر روی دیوارهای غارهای عصر حجر کنده کاری شده بوده و در نقاشی های مردم بابل به عنوان الگوی ترسیم سیاره ونوس به چشم می خورد. رازهایی مابین سیر استفاده از این علامت، طراحی های قدیمی از مدار حرکت سیاره ونوس و رب النوع معروف بیشتر وجود دارد که گاهی باعث این تفکر غلط میشود که پنتاگرام سمبل ایشتر است. در کتب آسمانی مخصوصا کتابهای یهودیان بسیار زیاد به پنتاگرامها اشاره شده است.پنتاگرام در جهان کهنپنتاگرام های اولیه اشکالی زمخت با شکل هندسی ناهمگون به صورت کنده کاری روی سنگهای عصر حجر داشتند. مردم آن زمان اعتقاد داشتند که این علامت معنایی روحانی و غیرمادی دارد. اعتقاد آنان بر این بود که رازی در شکل قرار گرفتن ستاره ها وجود دارد که بر انسان پوشیده است، آنها پنتاگرام را از روی شکل قرار گیری پنج سیاره برداشت کرده بودند که وقتی با خطی فرضی به هم اتصال پیدا می کردند به صورت مبهم شکل پنتاگرام را به خود می گرفت. نسل های بعدی بشر معانی مختلفی را از این شکل برداشت کردند معانی بسیار زیاد و اغلب مقدس و خداپرستانه.پنتاگرام ها به سومری ها برای نوشتن و استفاده از متون کمکهای زیادی کردند. این علامت نشان دهنده پنج سیاره مهم بود که با چشم غیر مسلح قابل رویت بودند. بعدها پنتاگرام به عنوان سمبل رب النوع زیبایی ونوس نیز شهرت یافت.برطبق نظریات ریاضی دان و فیلسوف یونانی فیثاغورث عدد پنج نماد انسان بود چون اعضای بدن انسان به پنج طرف تمایل داشتند، ( اگر دستها و پاها را ازهم باز کنید به شکل یک ستاره پنج پر در می آید)، او این تفکر را برای اولین بار در یونان پایه گذاری کرد که پنتاگرام نماد روح انسانی است و البته چون در آن زمان آفرینش انسان تابــع عناصر پنجگانه بود ( آتش ، آب ، خاک ، هوا ، روح ) پنج گوشه پنتاگرام اینگونه توصیف شد. طبق این تفکر انسان از این پنج عنصر به وجود می آمد. پیروان مکتب فیثاغورث طلسم پنج پر را به صورت آیینی مقدس حفظ کردند. آنها نام این آئین را HGIEIA نامیدند.و معتقدند ترکیبی از ابتدای نام یونانی عناصر آب، خاک، روح، آتش و هواست.خصوصیت منحصر به فردی که این سمبل را تا به امروز ماندگار کرده وابستگی شدید و همه جانبه آن به مسائل مقدس و خدایی آن است که در مقاطع زمانی مختلف و بین اقشار و نسلهای گوناگون کاربرد داشته است، چه این خدا خدای یگانه بوده یا خدایان متعدد. سپس با ظهور مسیح پنتاگرام جامه کریستین به تن کرد. می گویند بر تن مسیح با خنجر ستاره ای زخم زدند که پنج گوشه داشت ( شاید به همین ...
ما شهید می شویم ...
روزهای پایانی بهمن ماه هر سال یادآور نام و خاطره دو پرنده خونین بال است که هر لحظه یاد و نام آنان قلب ها را به لرزش درآورده و اشک ها را جاری می کند. آری چند روزی از آغاز عملیات والفجر ۸ گذشته بود و فاو به دست توانمند رزمندگان اسلام فتح شده و مراحل تثبیت مواضع بود. پاتک های سنگین و معروف زرهی بعثیون جهت باز پس گیری مواضع از دست رفته شروع شده و در این بین نقش تیپ مستقل ۱۵ امام حسن(ع) بیش از پیش احساس می شد. محسن زالی و امیر فاضل دو تن از بچه های پایگاه مقاومت امام سجاد(ع) بروجرد به همراه سایر همرزمان خود جانانه به پا خاسته و بر علیه خصم دون جهاد نمودند و در نهایت شاهد شهادت را به آغوش کشیدند. در احوال این شهیدان روایات فراوان است در سفر اخیر مشهد که توفیق همسفری با دکتر حمید رضا از همرزمان این عزیزان حاصل بود ایشان به نقل از شهید محسن زالی روایت می کرد روزی محسن به من گفت: ((حمید ما شهید می شویم شما درس بخوانید و در آینده خدمتگذار انقلاب و مردم باشید.)) روزی کفش نو پوشید که به مسجد برود هنوز چند قدمی از خانه دور نشده بود که احساس کرد با کفشی که نوست و همه ندارند که بپوشند نمی تواند راحت راه برود برگشت و کفش ها را به خاک آغشته کرد. امیر شهید در لحظات آخر با پای برهنه به تعقیب تانک های دشمن پرداخته و با گلوله مستقیم تانک به شهادت رسید. آری ما مدیون این همه ایثار و رشادت و فداکاری هستیم. آنان رفتند و با نثار جان این انقلاب و نهضت و انسانیت را بیمه نمودند آیا ما که مانده ایم پاسدار میراث گران سنگ آنان هستیم؟؟؟؟؟؟؟؟ امشب در خانه شهید محسن زالی سالگرد شهادتشان را با تلاوت قرآن گرامی می دارند برویم تا شاید نسیمی از آن همه پاکی و مردانگی به ما نیز بوزد... . شهید سید سعید حسینی، شهید امیر فاضل، شهید علی اشرف معظمی گودرزی، شهید سعدی موسیوند، شهید ناصر موسیوند، شهید مصطفی رافع، شهید حسین زندی، شهید مسعود ماکنانی، شهید علی کماسی، شهید محسن زالی، شهید سید علی گودرزی جانبازان.علی زراسوند،علیرضا حسن زاده؛سید محسن جده قریب،حجت الله پارسا،منوچهر موسیوند
ساخت چند ضلعی منتظم
پنج ضلعی منتظم: نوار بلند کاغذی آماده کنید که عرض یکسان داشته باشد. برای ساخت یک پنج ضلعی منتظم با این نوار به تر تیب زیر عمل کنید: 1. دو سر نوار را بگیرید و با آن یک گره ساده بزنید مانند شکل زیر: 2. گره را به آرامی سفت کنید و رد های کاغذ را صاف کنید. 3. نوار های اضافی را ببرید ،پنج ضلعی منتظم بوجود می آید. 4. گره را باز کنید و ذوزنقه های تشکیل شده را با هم بررسی و مقایسه کنید. هفت ضلعی منتظم: نوار بلند کاغذی آماده کنید که عرض یکسان داشته باشد. برای ساخت یک هفت ضلعی منتظم با این نوار به ترتیب زیر عمل کنید: 1. دو سر نوار را بگیرید و با آن یک گره ساده بزنید. (مانند پنج ضلعی منتظم) 2.گره را سفت نکنید و وسط گره (ناحیه ی 1) را در نظر داشته باشید. 3. مجددأ یک سر نوار را به قصد زدن گره دوم زیر سر دیگر برده ،و از ناحیه 1 (وسط گره اول) عبور دهید. 4.گره را به آرامی سفت کنید و رد های کاغذ را صاف کنید. 5.نوار های اضافی را ببرید ،هفت ضلعی منتظم بوجود می آید.
زوایای داخلی چند ضلعی
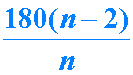
با استفاده از فرمول زیر می توان اندازه هر یک از زاویه ها را بدست آورد.n تعداد اضلاع است و جواب بدست آمده همان اندازه یک زاویه است. البته توجه داشته باشید که چند ضلعی باید منتظم باشد.نه مانند شکل زیر: مثال۱:اگر هر یک از زاویه های چند ضلعی ۱۳۵ درجه باشد،تعداد اضلاع این چند ضلعی چند تاست؟ مثال۲:هر یک از زاویه های داخلی یک دوازده ضلعی را بیابید؟
