هندسه گل آفتابگردان

هندسه طبیعت

  هندسه طبیعت هندسه بخش مهمی از قوانین همه ساختارهاست. برای شکل گیری ویژگی های خاص هر ساختار، چگونگی روابط و چیدمان اجزاء بسیار مهمتر از خود اجزاء است. با وجود اجزاء مشترک در اشیاء و موجودات هندسه متفاوت و نحوه چیدمان آنها باعث پدید آمدن آثار متفاوت می شود خداوند عالم و جهان طبیعت را به زبان ریاضی نگاشته است ( گالیله )   در آسمان ماه و خورشید و ستارگان و بر روی زمین ، کوهها و درختها و میوه ها  و گیاهان ، و نیز موجهای دریا و حلزونها و نمونه های دیگر ، همه و همه شکل های منظم هندسی دارند . آشناترین شکل را ، سیمای خورشیدی دارد  کهکشانها نیز شکل های خاصی دارند . کهکشان مارپیچی که شکل هندسی جالبی دارد ، این کهکشان مشابه یکی از انواع منحنی است که در هندسه به نام منحنی مارپیچی مورد بررسی قرار می گیرد . به مرور و در اثر تجربه پی برد که بهتر است برای ساختن ظروف و دیگر وسایل نگهداری غذا ، از این شکل ها استفاده کند . او شکل دایره را هر روز بر سیمای خورشید می دید از طرفی به تجربه دریافته بود که اگر سنگریزه ای را در آب بیندازد ، موجی هایی بر سطح آب تشکیل می شود ، که شکل های مشابه شکل خورشید است . انسان نخستین از الگوها و شکل های هندسی منظمی که در زیستگاه خود می دید برای ساختن اشیای مورد نیازش بهره می گرفت . شکل مستقیم و کشیده درختان را برای ساختن نیزه های شکار  الگوی او حتی با مقایسه اشکال مستقیم و خمیده موجود در طبیعت دریافته بود که اگر فاصله بین دو نقطه را به صورت مستقیم طی کند کوتاهترین راه را انتخاب کرده است . او کوهها و تپه های مخروطی شکل را بر پهنه زمین می دید و در ساختن آلونکها و مأواهای مخروطی شکل خویش به عنوان الگو از آنها الهام می گرفت . مفاهیم خطوط موازی و قائم و افقی را درک کرد و در پنای پناهگاههای خویش از آنها سود می جست . به دنبال افزایش شناخت و آگاهی انسان از طبیعت پدیده ها و موجودات دیگری نیز برای او مطرح شدند که ساختمان آنها مدل ، الگو هستند . برش یک سیب که الگوی هندسی دارد . طرز آرایش دانه ها در گل آفتابگردان به شکل منحنی های مارپیچ دو گانه ای است که در دو جهت مخالف نظم گرفته اند . بیشتر گل های طبیعت از الگو و مدل خاصی تبعیت می کنند . گلبرگهای آنها غالبا به شکل « متقارن » است که یک مفهوم ریاضی است . شکل بیشتر گل ها مشابه منحنی هایی است که معادله خاص دارد .   کندوی زنبور عسل که ساخته زنبور عسل است از شش ضلعی هایی تشکیل شده است که هر کدام محل ذخیره عسل است .  این شش ضلعی های منظم را سلول می نامند این تصادفی نیست که زنبورها سلول های  « شان » عسل را به شکل شش ضلعی می سازند شکل شش ضلعی سول ها کار همزمان سه زنبور را ...

تناسب در معماری

oتناسب چیست؟ oتناسب مجموعه ای از نسبت هاست،مقایسه ی دو کیفیت یا کمیت نظیر اندازه یا مقدار است. oو از این رو نسبت ها نشان دهنده ی واحدی از یک اختلاف یا تفاوت تلقی می شوند،واین تفاوت ها جوابگوی حداقل یکی از نیروهای حسی انسان است،از سوی دیگر در فرایند ادراک از آنجا که کمیت ادراکی جهان متکی بر ساختار الگوهای پیچیده ای از تفاوت هاست.یک مسبت ساده نیز جدا ازیک تصویر بنیادی برای فعالیت های ادراکی از اساسی ترین فرآیندهای هوش نیز تلقی می شود oتناسبات به دلیل در بر گیرندگی نسبت های گوناگون از پیچیدگی بیشتری برخوردار است.آنگاه که تناسب نسبت ها متکی بر تفاوت های کمی و همسان را شامل می شود پیچیدگی های قابل تبینی عرضه می کند.اما در عمل و به ویژه در عرصه ی معماری "تناسب" نسبت های مقایسه ای کمیت ها و کیفیت های مختلف ناهمسانی را شامل می شود.از این رو درک آن پیچیده تر است.   oاگر تناسب را به عنوان نمونه ای برای فعالیت ادراک بر اساس شناخت تفاوت ها قرار دهیم در این میان تناسب طلایی"تناسب زرین" به یک معنی می تواند به عنوان فرا عقل،الهی یا آسمانی تلقی شود.در واقع این نخستین حاصل یک بودگی و تنها آفریننده ممکن ثنویت درباره ی واحد اولی یا اولین تقسیم واحد می تواند داشته باشد.نخستین بار از هنگامی که بشر درباره ی اشکال هندسی این تناسبات و دنیای آن به تفکر پرداخت،ملاحضات فلسفی،طبیعی و زیبایی شناختی بسیاری که آن را احاطه کرده بود چشم گیر است.در هنر و معماری یونان نیز این تناسبات نقش غالب را ایفا می کند ولی در بناهای تاریخی گوتیک در قرون وسطی وناگهان اعتبار خود را از دست می دهد،لیکن در عصر رنساسن بار دیگر اعتبار خود را باز می یابد.اگر چه جنبه های گوناگون طبیعت را که ماییه الهامه هنرمندان است فراگیر می سازد.نمی توان گفت آنکه در هرجایی که کمال مطلوب یا زیبایی خاص با هماهنگی شکل وجود داشته باشد تأثیر تناسب طلایی به چشم می خورد و آن به یادآورنده ی وابستگی جهان مخلوق و مبدأ کمال و نیز تکامل بلقوه ی اوست. oمبحث تناسب به طور عامه در هنر و خاص در ادبیات هنر و معماری معاصر ما مضمون غریبی می نماید.تناسب در شکل کلی متکی بر علم هندسه و ریاضی در  جای خود و در شکل تخصصی خودارزش انکار ناپذیری در مبادی درک هنر دارد.واز ملاحضات اساسی تلقی می شود.   oترکیب طلایی  یا توالی فیبوباچی در ستاره ی داوود توسعه یافته: oهنرمندان قدیمی برای اضافه نمودن حس توازن و شکوه به یک صحنه،مجسمه یا بنا مدت ها از ترکیب تناسب طلایی استفاده کردند.نرکیب مزبور یم تناسب ریاضی بر اساس نسبت 10618/1 بوده و در اغلب مواقع در طبیعت مثلاً در صدف های دریایی و الگوی دانه های گل آفتابگردان ...

عدد طلایی

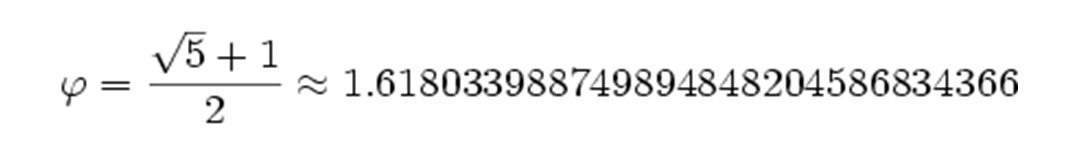
نسبت طلایی یکی از زیبایی ‌های دنیای ریاضی است که رد آن را در جای‌ جای طبیعت می‌توان مشاهده کرد ، از نسبت طول اندام‌های انسان گرفته تا چشم‌ نواز ترین آثار معماری و حتی رشد مارپیچ دانه‌های گل آفتابگردان! نسبت طلایی ، عددی غیرگویا ( گنگ ) است که با حرف یونانی φ نمایش داده می‌شود. بسیاری از هنرمندان معتقدند شکل‌هایی که در آن‌ها نسبت طلایی رعایت شده است ، چشم‌ نواز ترین شکل‌های ممکن را تشکیل می‌دهند. مثال معروف آن‌ها ، کاغذهای استاندارد سری A ( مانند کاغذ A4 به ابعاد 210×297 میلی‌متر ) است که در آن‌ها نسبت طول به عرض برابر نسبت طلایی است. نسبت طلایی هم‌چنین از رشته فیبوناچی نیز به دست می‌آید. رشته فیبوناچی یکی از جالب‌ترین رشته‌های اعداد است که در آن ، عدد بعدی برابر حاصل‌جمع دو عدد قبلی است ... ، 144 ، 89 ، 55 ، 34 ، 21 ، 13 ، 8 ، 5 ، 3 ، 2 ، 1 ، 1 ، 0 و هرچه این رشته بیشتر ادامه پیدا کند ، نسبت عدد بزرگ‌تر به عدد قبلی به نسبت طلایی نزدیک‌تر می‌شود. مایکل بلیک ، موسیقیدانی که به ریاضیات علاقه دارد ، قطعه‌ای موسیقی را بر اساس نسبت طلایی نوشته است. او برای این کار ، رقم‌های اعشار نسبت طلایی را به صورت نت‌های موسیقی بازنویسی کرده و حاصل آن‌ را به صورت یک کلیپ ویدیویی آماده کرده است. عدد طلایی در رياضيات چیست؟ عدد طلائی عددی است ، تقریباً مساوی 1.618 ، که خواص جالب بسیاری دارد ، و به علت تکرار زیاد آن در هندسه ، توسط ریاضیدانان کهن مطالعه شده است. اشکال تعریف شده با نسبت طلائی ، از نظر زیبائی شناسی در فرهنگ های غربی دلپذیر شناخته شده ، چون بازتابنده خاصیتی بین تقارن و عدم تقارن است. دنیای اعداد بسیار زیبا ست و شما می توانید در آن شگفتی های بسیاری را بیابید. در میان اعداد برخی از آن ها اهمیت فوق العاده ای دارند ، یکی از این اعداد که سابقه آشنایی بشر با آن به هزاران سال پیش از میلاد می رسد عددی است به نام ( نسبت طلایی ) یا  Golden Ratio، این نسبت هنوز هم بارها در هنر و طراحی استفاده می شود. نسبت طلائی به نام های برش طلائی ، عدد طلائی ، نسبت الهی نیز شناخته می شود. نحوه محاسبه نسبت عدد طلائی : پاره خطی را در نظر بگیرید و فرض کنید که آن را به گونه ای تقسیم کنید که نسبت بزرگ به کوچک معادل نسبت کل پاره خط به قسمت بزرگ باشد. به شکل توجه کنید. اگر این معادله ساده یعنی   را حل کنیم (کافی است به جای b عدد 1 قرار دهیم ،  بعد a را به دست آوریم) به نسبتی معادل تقریبا 1.61803399 یا 1.618 خواهیم رسید.کاربردها :برش اهرام و نسبت طلائی  :شاید باور نکنید اما بسیاری از طراحان و معماران بزرگ برای طراحی محصولات خود امروز از این نسبت طلایی استفاده می کنند. چرا که ...

دنباله فیبوناچی در طبیعت

پنج كار وي در اين مدت به صورت زير بود: لئوناردو فيبوناچي در سال 1170 در شهر پيزا در كشور ايتاليا به دنيا آمد. پدرش  جليلمو بوناچي تاجر بود. پدرش وي را در سال 1192 با خود به بوجيا برد.پدر لئو ناردو وي را براي آموزش كار و تجارت به كشور هاي مصر، سيريا ، يونان ،سيسيل و چند كشور ديگر فرستاد . لئوناردو از اين مو قعيت استفاده كرد و در خلال اين سفر ها با فنون محاسباتي در اين كشورها آشنا شد وآنها را فرا گرفت. حدود سال 1200 بود كه لئوناردو به شهر خودش پيزا بازگشت و پس از آن شروع به كاركردن بر روي سيستم ابداعي خود شد. كار بر روي ليبر آباچي (1228-1202) ، هندسه كاربردي (1220-1221) ، نامه بدون تاريخ به تئودور (1225) ، مجموعه راه حل هاي مس‍‍أله هايي كه فردريك دوم به او داده بود(1225) ، كتاب نظريه اعداد كه در آن به حل معادله درجه دوم اشاره شده بود. و همين كارها باعث شهرت وي در رياضيات شد. اتفاقاتي كه پس از سال 1228 بر وي اتفاق افتاده است بر كسي روشن نيست و تنها نكته اي كه به آن اشاره شده است،اينست كه به پاس خدماتي كه او انجام داده بود ، از طرف شاه برايش مقرري اي در نظر گرفته شده است. لئوناردو فيبوناچي چندي پس از سال 1240 و به احتمال زياد در پيزا چشم از جهان فرو بست.دنباله فيبوناچي و نسبت طلائي: 0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , … در دنباله فيبوناچي هر درايه حاصل جمع دو درايه قبل از خود مي باشد:      fn=fn-1+fn-2 , f1=1 , f2=1                                 نكته جالب توجه در مورد اين دنباله اينست كه حاصل تقسيم هر دو عدد متوالي از اين دنباله بسيار به نسبت طلائي نزديك است. 34 / 55 = 0.618                   55 / 34 = 1.618 89 / 55 = 1.618                   55 / 89 = 0.617 377 / 233 = 1.618               233 / 377 = 0.618 فيبوناچي در گياهان: 1- آفتابگردان : يكي از جالبترين مثال ها در مورد فيبوناچي در طبيعت همين گل آفتابگردان است. دانشمندان پس از شمارش تعداد مارپيچ هاي موجود در سر گل آفتابگردان دريافتند كه يك دسته از مارپيچ هاي كوچك از داخل به طرف بيرون در جهت حركت عقربه هاي ساعت و مارپيچ هاي بزرگ در خلاف جهت حركت عقربه هاي ساعت قرار دارند.وجود اين دو نوع مارپيچ موجي زيبا را در سر گل آفتابگردان ايجاد مي كند. همچنين دو رابطه زير را آشكار مي سازد: الف ) جفت ها هميشه به درايه هاي دنباله فيبوناچي نزديك اند: يك جفت ميتواند 21 و34 و جفت بعدي مي تواند 34 و 55 باشد. ب ) عدد حاصل از تقسيم اين عددها به نسبت طلائي نزديك است.فيبوناچي در جانوران: 1- DNA  : مولكول DNA از 2 زنجيره پلي نوكلئوتيدي ساخته شده است. بين بازهاي آلي آدنين و تيمين 2 پيوند هيدروژني و بين بازهاي آلي گوانين و سيتوزين 3 پيوند هيدروژني وجود دارد. مطلب جالب ...

لوح حقوق بشر کورش کبیر

مرایاد بگیر

.... ﻣﺮﺍ ﯾﺎﺩ ﺑﮕﯿﺮ نه مثل جبر...  نه مثل هندسه ...!  نه ﻣﺜﻞ ۱ منهای ۱ ﮐﻪ ﻫﻤﯿﺸﻪ ۰ ﻣﯿﺸﻮﺩ  ﻣﺮﺍ ﯾﺎﺩ ﺑﮕﯿﺮ مثل نیمکت آخر...  زنگ آخر...  ﻭ ﺩﺳﺘﺎﻧﯽ ﮐﻪ ﻧﺎﻡ ﺗﻮ ﺭﺍ ...  ﻣﺪﺍﻡ ﺭﻭﯼ ﭼﻮﺏ ﺣﮏ ﻣﯿﮑﺮﺩ  مرا یاد بگیر....!          

نسبت طلایی-عدد مقدس-عدد الهی-راز هندسه کائنات

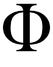
همون طور که میدونید عدد فی(Φ) اسمهای دیگه ای هم داره از جمله عدد الهی یا عدد مقدس عدد فی(Φ) یا همان عدد طلایی و یا به قول هنرمندان٬ عدد الهی است. گفته اند که عدد فی بعضی از رازهای عجیب کائنات رو آشکار کرده که به برخی از این موارد اشاره میکنیم.  همه دوستان با دنباله فیبوناچی آشنا هستند.در این دنباله هر عدد برابراست با مجموع دو عدد قبلی اش.:... ,0،1,1,2,3,5,8,13,21,34,55,89,144,233مثلا ۱+۱=۲ ٬ ۲+۱=۳ ٬ ۳+۲=۵ ٬ ۵+۳=۸ و ....حال اگر هر عدد را در این دنباله بر عدد قبلی خود تقسیم کنیم ٬ هرچه به سمت راست دنباله پیش میریم به یک عدد شگفت انگیزی میرسیم که به عدد فی معروف است:1=1÷12=1÷21.5=2÷3...1.66=3÷5هر چه جلوتر میریم به یک عددی نزدیک میشیم برابر با 1.618033 که به طور اختصارفی را برابر با 1.618 می خوانند.۱- در هر کندوی عسل در سراسر جهان ٬ نسبت زنبورهای ماده به زنبورهای نر برابر 1.618 است یعنی عدد فی.۲- در صدف نرم تنان نسبت قطر هر مارپیچ به مارپیچ قبلی اش عدد 1.618 است یعنی عدد فی.۳-در گل افتابگردان اگه دقت کنید تخمه ها به صورت مارپیچ کنار هم چیده شده اند.قطر هر مارپیچ به مارپیچ قبلی اش عدد 1.618 است یعنی عدد فی.۴- فاصله سر تا زمین تقسیم بر فاصله ناف تا زمین میشه عدد 1.618 یعنی عدد فی.۵- فاصله شانه تا نوک انگشتان تقسیم بر فاصله آرنج تا نوک انگشتان عدد 1.618 یعنی عدد فی۶-فاصله انتهای کمر تا زمین تقسیم بر قاصله زانو تا زمین میشه عدد 1.618 یعنی عدد فی۷- فاصله مفاصل انگشتان تا نوک انگشتان تقسیم بر فاصله مفصل بعدی تا نوک انگشتان عدد 1.618 یعنی عدد فی۸- در یک گردباد نسبت قطر مارپیچ بزرگتر به مارپیچ کوچکترش میشه عدد شگفت انگیز فی۹- در یک کهکشان نسبت قطر مارپیچ بزرگتر به مارپیچ کوچکترش میشه عدد شگفت انگیز فی۱۰- در حلزون گوش داخلی نسبت قطر مارپیچ بزرگتر به مرپیچ کوچکترش میشه عدد شگفت انگیز فیمختون سوت کشید ... نه!!!نسبت طلایی در طبیعت، آثار هنری و معماری متعددی مشاهده می شود. به عنوان نمونه نسبت طلایی اساس نقاشی مشهور مرد ویترووین داوینچی است. نمای معبد پارتنون در آتن یک مستطیل طلایی کامل است. خانه مارپیچی شکل حلزون ها یک نمونه بسیار مشهور از کاربرد نسبت طلایی در طبیعت است همانگونه که مارپیچ مولکول DNA انسان نیز اینگونه است.توضیح: عدد فی برابر است با ۱.۶۱۸ در قرن 12، لئوناردو فيبوناچي ( Leonardo Fibonacci ) دنباله ي مشهور خود را معرفي نمود. جمله ي بعدي برابر مجموع دو جمله ي قبلي خود مي باشد. 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . . عدد في از دنباله ي فيبوناچي مشتق شده است، تصاعد مشهوري كه شهرتش تنها به اين دليل نيست كه هرجمله با مجموع دو جمله ي پيشين خود برابري مي كند. بلكه به اين دليل است كه خارج قسمت هر دو جمله ...