معادلات دیفرانسیل با مشتقات جزئی
معرفی کتاب معادلات دیفرانسیل با مشتقات جزئی و کاربردهای آن در علوم ومهندسی

سرفصل کتاب: تعاریف و مفاهیم اساسی معادلات مرتبه اول شبه خطی و روش مشخصهها مدلهای ریاضی دستهبندی معادلات مرتبه دوم خطی مسئله کوشی و معادلات موج سریها و انتگرالای فوریه با کاربردها روش جداسازی متغیرها مسائل مقدار ویژه و توابع خاص مسائل مقدار مرزی و کاربردها مسائل مقدار مرزی با ابعاد بالاتر توابع گرین و مسائل مقدار مرزی روشهای تبدیل انتگرال و کاربردها معادلات دیفرانسیل جزئی غیرخطی و کاربردها روشهای تقریبی و عددی جداول تبدیل انتگرال این کتاب ترجمهای از کتاب Tyn Myint-U and Lokenath Debnath, Linear Partial Differential Equations for Scientists and Engineers, Fourth Edition, Springer, 2007. میباشد که در حال حاضر توسط مرکز نشر دانشگاهی زیر چاپ است. دانلود فهرست کامل کتاب
دانلود جزوه ریاضیات مهندسی

دانلود جزوه ریاضیات مهندسی,spowpowerplant, Blog,مهندسی مکانیک,وبلاگ یک مهندس,اسپاو, Weblog,همه چیز درباره نیروگاه,مهندسی مکانیک,برق و الکترونیک,پمپ پایپینگ توربین,مهندسی شیمی,تحقیق,داستان کوتاه,دانلود کتاب جزوه مقاله پروژه,پروژه تحقیق پایان نامه,مهندسی,Engineer,مدیریت,دانلود کتابهای مهندسی,معرفی و نقد فیلم و کتاب,دانلود جزوه,دانلود مقاله,توربین,نیروگاه,spow, Persian,Iran, Iranian,Google,Yahoo,MSN, Weblogs, Blogs"> وبلاگ یک مهندس... - دانلود جزوه ریاضیات مهندسیوبلاگ یک مهندس... دانلود جزوه ریاضیات مهندسی دانلود جزوه ریاضیات مهندسیدانلود جزوه تایپ شده و کامل ریاضیات مهندسیجزوه ریاضیات مهندسی که دراین پست برای دانلود اماده ساخته ایم سرفصل های زیر را شامل میشود : فصل اول : سری های فوریه و حل معادلات با مشتقات جزئیتابع متناوبانتگرال های مثلثاتی مورد لزومضرایب فوریه - اویلرمثال هایی از سری های فوریهقضیه دیریکلهاتحاد پارسوالتوابع زوج و فردتمریناتفصل دوم : انتگرال های فوریهانتگرال فوریهتبدیل فوریهفصل سوم : معادلات دیفرانسیل با مشتقات جزئیمعادلات دیفرانسیل با مشتقات جزئیطبقه بندی معادلات با مشتقات نسبی خطیمعادلات دیفرانسیل مهمروش های حل معادلات دیفرانسیل خطیمعادلات دیفرانسیل با مشتقات نسبی اویلرحل معادلات دیفرانسیل خطی به روش متغیرهای جدا از همحل معادلات دیفرانسیل خطی با استفاده از تبدیل لاپلاستمریناتفصل چهارم : عدد مختلطاعداد مختلطنمایش مثلثاتی یا قطبی اعداد مختلطمحاسبه ریشه های یک عدد مختلطتوابع مختلطمعادلات کش - ریمنتوابع مقدماتی مختلطتابع لگاریتمانتگرال گیری در صفحه مختلطسری های مختلطنقاط غیرعادی (ویژه)سری لورانقضیه مانده هانگاشت همدیستبدیل های مهمتمریناتجزوه 84 صفحه ای ریاضیات مهندسی را از لینک زیر دریافت نمایید:دانلود جزوه ریاضیات مهندسیدانلود کنید.پسورد : www.spowpowerplant.blogfa.com
معادلات دیفرانسیل(معمولی و مشتقات نسبی)، حل عددی ODE , PDE و تبدیلات لاپلاس

پاورپوینت معادلات دیفرانسیل(آقای دکتر صفار اردبیلی) معادلات دیفرانسیل(آقای دکتر صفار اردبیلی) معادلات دیفرانسیل(آقای استاد نیسی) معادلات دیفرانسیل معمولی و کاربرد آنها(آقای دکتر بیژن شمس) معادلات دیفرانسیل موسسه آموزش عالی آزاد پارسه ==>> فصل 1و2 فصل 3و4 و5 معادلات دیفرانسیل آقای دکتر معتقدی (درس و سوالات چهار گزینه ای) معادلات دیفرانسیل معادلات دیفرانسیل مرتبه دوم معمولی (به زبان لاتین) معادلات دیفرانسیل (به زبان لاتین) Solving Ordinary Differential Equations I روشهای تفاضلات محدود برای حل عددی معادلات دیفرانسیل ode حل عددی معادلات دیفرانسیل با مشتقات نسبی(AMES) قابل استفاده برای دانشجویان کارشناسی ارشد ریاضی روشهای تفاضلات متناهی و عناصر متناهی برای حل عددی PDE Elementary Theoretical Methods in PDE (Ordinary Differenatial Equations(ODE مقدمه ای بر روش های عددی در معادلات دیفرانسیل جزوه معادلات دیفرانسیل معمولی(آقای دکتر مرشدی) جزوه معادلات دیفرانسیل جزوه معادلات دیفرانسیل حل عددی معادلات دیفرانسیل معمولی و جزئی متمم معادلات دیفرانسیل و کاربرد آنها معادلات دیفرانسیل با مشتقات جزیی تبدیلاتلاپلاس (به زبان لاتین) جزوه تبدیلات لاپلاس موسسه آموزش عالی پارسه (منبع:www.ieun.ir) روش های عددی برای تبدیل معکوس لاپلاس
معادلات دیفرانسیل
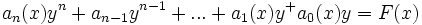
معادلات دیفرانسیل مقدمه نوع (عادی یا جزئی) مرتبه درجهساختار صور مختلف معادلات دیفرانسیل معادله دیفرانسیل همگن معادلات دیفرانسیل مرتبه دوم معادلات دیفرانسیل خطیحل معادلات دیفرانسیلی خطی مرتبه n ام به توسط سریهای توانی کاربردها مباحث مرتبط با عنوان مقدمه معادله دیفرانسیل معادلهای است که شامل یک یا چند مشتق یا دیفرانسیل باشد. معادلات دیفرانسیل بر اساس ویژگیهای زیر رده بندی میشوند: نوع (عادی یا جزئی) معادله شامل متغیر مستقل x ، تابع (y = f(x و مشتقات f را یک معادله دیفرانسیل عادی مینامیم. معادله ای متشکل از یک تابع مجهول با بیش از یک متغیر مستقل همراه با مشتقات جزئی آن معادله دیفرانسیل جزئی می نامیم. مرتبه که عباترت است از مرتبه مشتقی که بالاترین مرتبه را در معادله دارد. درجه نمای بالاترین توان مشتقی که بالاترین مرتبه را در معادله دارد، پس از حذف مخرج کسرها و رادیکالهای مربوط به متغیر وابسته و مشتقاتش. معمولا یک معادله دیفرانسیل مرتبه n جوابی شامل n ثابت دلخواه دارد، این جواب را جواب عمومی مینامند. ساختار معادلات دیفرانسیل ساختارهای متفاوتی هستند و هر ساختار ویژگیهای متفاوتی دارد: معادلات مرتبه اول از درجه اول با متغیرهای جدایی پذیر همگن خطی (برنولی) با دیفرانسیلهای کامل معادلات مرتبه دوم معادلات خطی با ضرایب ثابت: الف) همگن ب) ناهمگن. تکنیکهای تقریب زدن: الف) سریهای توانی ب) روشهای عددی. صور مختلف معادلات دیفرانسیل معادله دیفرانسیل مرتبه اول از درجه اول را همواره میتوان به صورت زیر در آورد که در آن M و N معرف توابعی از x و y هستند. Mdx + Ndy = 0در معادله فوق هرگاه M فقط تابعی از x و N فقط تابعی از y باشد. به صورت معادله جدایی پذیر مرتبه اول است. در این صورت با انتگرال گیری از هر جمله جواب بدست میآید. یعنی: M(x) dx+ ∫N(y) dy = C∫ معادله دیفرانسیل همگن گاه معادله دیفرانسیلی را که متغیرهایش جدایی پذیر نیستند با تعویض متغیر میتوان به معادلهای تبدیل کرد که متغیرهایش جدایی پذیر باشند، چنین معادلهای را همگن مینامند. معادله دیفرانسیل خطی مرتبه اول را همیشه میتوان به صورت متعارف زیر در آورد که در آن P و Q توابعی از x هستند. dy/dx + py = Qمعادله را که بتوان آن را به صورت: M (x,y) dx + N(x,y) dy = 0نوشت و دارای ویژگی زیر باشد کامل نامیده میشود. زیرا طرف چپ آن یک دیفرانسیل کامل است. M/∂y = ∂N/∂x∂ معادلات دیفرانسیل مرتبه دوم یک معادله دیفرانسیل مرتبه دوم در حالت کلی به صورت زیر است: F (x,y,dy/dx,d2y/dx2) = 0این گونه معادلات را معمولا با یک متغیر مناسب مثل dy/dx = p به معادلات دیفرانسیل نوع اول تبدیل کرد و با جاگذاری در معادله مربوط به ...
