معادلات دیفرانسیل
معادلات دیفرانسیل
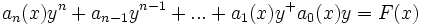
معادله دیفرانسیل معادلهای است بیانگر یک تابعی از یک یا چندین متغیر وابسته و مشتقهای مرتبه های مختلف آن متغیرها. بسیاری از قوانین عمومی طبیعت (در فیزیک، شیمی، زیستشناسی و ستارهشناسی) طبیعیترین بیان ریاضی خود را در زبان معادلات دیفرانسیل مییابند. کاربردهای معادلات دیفرانسیل همچنین در ریاضیات، بویژه در هندسه و نیز در مهندسی و اقتصاد و بسیاری از زمینههای دیگر علوم فراواناند. معادلات دیفرانسیل در بسیاری پدیده های علوم رخ می دهند. هر زمان که یک رابطه بین چند متغیر با مقادیر مختلف در حالت ها یا زمان های مختلف وجود دارد و نرخ تغییرات متغیرها در زمان های مختلف یا حالات مختلف شناخته شده است میتوان آن پدیده را با معادلات دیفرانسیل بیان کرد. به عنوان مثال در مکانیک، حرکت جسم بوسیله سرعت و مکان آن در زمان های مختلف توصیف می شود و معادلات نیوتن به ما رابطه بین مکان و سرعت و شتاب و نیروهای گوناگون وارده بر جسم را میدهد. در چنین شرایطی می توانیم حرکت جسم را در قالب یک معادله دیفرانسیل که در آن مکان ناشناخته جسم تابعی از زمان است بیان کنیم. شاخه بندی متدهای حل معادلات دیفرانسیل بسیار مرتبط با نوع معادله هستند. معادلات دیفرانسیل را به طور کلی به دو دسته می توان تقسیم کرد. معادلات دیفرانسیل عادی: در این نوع معادلات تابع جواب دارای تنها یک متغیر مستقل است. معادلات دیفرانسیل جزیی: در این نوع معادلات تابع جواب دارای چندین متغیر مستقل می باشد. هر دو نوع این معادلات را می توان از دیدگاه خطی یا غیر خطی بودن تابع جواب هم دسته بندی کرد. معادلات دیفرانسیل مشهور قانون دوم نیوتن در مکانیک معادلات همیلتون در مکانیک کلاسیک معادلات ماکسولدر الکترو مغناطیس معادلات پواسن مسئله منحنی کوتاهترین زمان. فرمول انیشتین. قانون گرانش نیوتن. معادله موج برای تار مرتعش. نوسانگر همساز در مکانیک کوانتومی. نظریه پتانسیل. معادله موج برای غشای مرتعش. معادلات شکار و شکارچی. مکانیک غیر خطی. مسئلهٔ مکانیکی آبل. نوع(عادی یا جزئی) معادله شامل متغیر مستقل x ، تابع (y = f(x و مشتقات f را یک معادله دیفرانسیل عادی مینامیم.معادله ای متشکل از یک تابع مجهول با بیش از یک متغیر مستقل همراه با مشتقات جزئی آن معادله دیفرانسیل جزئی می نامیم. مرتبه که عباترت است از مرتبه مشتقی که بالاترین مرتبه را در معادله دارد. درجه نمای بالاترین توان مشتقی که بالاترین مرتبه را در معادله دارد، پس از حذف مخرج کسرها و رادیکالهای مربوط به متغیر وابسته و مشتقاتش. معمولا یک معادله دیفرانسیل مرتبه n جوابی شامل n ثابت دلخواه دارد، این جواب را جواب عمومی مینامند. ساختار معادلات ...
معادلات دیفرانسیل
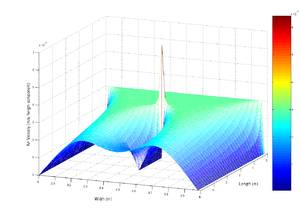
معادله دیفرانسیل یک معادلهای ریاضی است و بیانگر یک تابع مجهول از یک یا چند متغیر مستقل و مشتقهای مرتبههای مختلف آن نسبت به متغیرهای مستقل است. بسیاری از قوانین عمومی طبیعت (در فیزیک، شیمی، زیستشناسی و ستارهشناسی) طبیعیترین بیان ریاضی خود را در زبان معادلات دیفرانسیل مییابند. کاربردهای معادلات دیفرانسیل همچنین در ریاضیات، بویژه در هندسه و نیز در مهندسی و اقتصاد و بسیاری از زمینههای دیگر علوم فراواناند. معادلات دیفرانسیل در بسیاری پدیدههای علوم رخ می دهند. هر زمان که یک رابطه بین چند متغیر با مقادیر مختلف در حالتها یا زمانهای مختلف وجود دارد و نرخ تغییرات متغیرها در زمانهای مختلف یا حالات مختلف شناخته شده است میتوان آن پدیده را با معادلات دیفرانسیل بیان کرد. به عنوان مثال در مکانیک، حرکت جسم بوسیله سرعت و مکان آن در زمانهای مختلف توصیف میشود و معادلات نیوتن به ما رابطه بین مکان و سرعت و شتاب و نیروهای گوناگون وارده بر جسم را میدهد. در چنین شرایطی می توانیم حرکت جسم را در قالب یک معادله دیفرانسیل که در آن مکان ناشناخته جسم تابعی از زمان است بیان کنیم. محتویات ۱ شاخه بندی۲ معادلات دیفرانسیل مشهور۳ پیوندهای بیرونی۴ منابع شاخه بندی متدهای حل معادلات دیفرانسیل بسیار مرتبط با نوع معادله هستند. معادلات دیفرانسیل را به طور کلی به دو دسته می توان تقسیم کرد. معادلات دیفرانسیل معمولی: در این نوع معادلات تابع جواب دارای تنها یک متغیر مستقل است. معادلات دیفرانسیل با مشتقات پارهای: در این نوع معادلات تابع جواب دارای چندین متغیر مستقل میباشد. هر دو نوع این معادلات را می توان از دیدگاه خطی یا غیر خطی بودن تابع جواب هم دسته بندی کرد. مجسم سازی جریان هوا به داخل لوله که با معادلات ناویر-استوکس، مدل سازی شدهاست، مجموعهای از معادلات دیفرانسیل جزئی معادلات دیفرانسیل مشهور قانون دوم نیوتن در دینامیک (مکانیک)معادلات همیلتون در مکانیک کلاسیکواپاشی هستهای در فیزیک هستهایمعادله موجمعادلات ماکسول در الکترومغناطیسمعادلات پواسنمعادله لاپلاس که توابع هارمونیک را تعریف میکندمسئله منحنی کوتاهترین زمان.فرمول انیشتین.قانون گرانش نیوتن.معادله شرودینگر در مکانیک کوانتوممعادلات ناویه-استوکس در دینامیک شارههامعادلات کوشی-ریمان در آنالیز مختلطمعادله پواسون-بولتزمن در دینامیک ملکولیمعادله موج برای تار مرتعش.نوسانگر همساز در مکانیک کوانتومی.نظریه پتانسیل.معادله موج برای غشای مرتعش.معادلات شکار و شکارچی.مکانیک غیر خطی.مسئلهٔ مکانیکی آبل.
دانلود کتاب معادلات دیفرانسیل از دکتر مسعود نیکوکار

دانلود کتاب معادلات دیفرانسیل از دکتر مسعود نیکوکار نام کتاب : معادلات دیفرانسیلنام نویسنده : دکتر مسعود نیکوکارزبان : پارسیتعداد صفحه : 527قالب : PDFحجم : 33.6 معادله دیفرانسیل معادلهای است بیانگر یک تابعی از یک یا چندین متغیر وابسته و مشتقهای مرتبههای مختلف آن متغیرها. بسیاری از قوانین عمومی طبیعت ( در فیزیک، شیمی، زیستشناسی و ستارهشناسی ) طبیعیترین بیان ریاضی خود را در زبان معادلات دیفرانسیل مییابند. کاربردهای معادلات دیفرانسیل همچنین در ریاضیات، بویژه در هندسه و نیز در مهندسی و اقتصاد و بسیاری از زمینههای دیگر علوم فراواناند. معادلات دیفرانسیل در بسیاری پدیدههای علوم رخ می دهند. هر زمان که یک رابطه بین چند متغیر با مقادیر مختلف در حالتها یا زمانهای مختلف وجود دارد و نرخ تغییرات متغیرها در زمانهای مختلف یا حالات مختلف شناخته شده است میتوان آن پدیده را با معادلات دیفرانسیل بیان کرد. به عنوان مثال در مکانیک، حرکت جسم بوسیله سرعت و مکان آن در زمانهای مختلف توصیف میشود و معادلات نیوتن به ما رابطه بین مکان و سرعت و شتاب و نیروهای گوناگون وارده بر جسم را میدهد. در چنین شرایطی می توانیم حرکت جسم را در قالب یک معادله دیفرانسیل که در آن مکان ناشناخته جسم تابعی از زمان است بیان کنیم. سرفصلهای کتاب :معادلات دیفرانسیل معمولیمعادلات دیفرانسیل مرتبه اولمعادلات دیفرانسیل معمولی مرتبه دوم و بالاترحل معادلات با استفاده از سریهادستگاه معادلات دیفرانسیل خطیتبدیل لاپلاس برای دانلود با حجم 33.6 MB کلیک کنید
معادلات دیفرانسیل
بنام حضرت دوست که هرچه داریم از اوست باتوجه به اینکه معادلات دیفرانسیل کار برد زیادی درمهندسی و فیزیک و ....دارد تصمیم گرفتم مطالبی در مورد حل انها ارایه نمایم معادلات دیفرانسیل معمولی(رشته ریاضی) سرفصل معادلات دیفرانسیل عنوان فصل اول: معادله دیفرانسیل مرتبه اول 1: ماهیت معادلات دیفرانسیل و طبقه بندی آنها 2: معادله دیفرانسیل جدا شدنی و تبدیل به آن 3: معادله دیفرانسیل همگن و تبدیل به آن 4: دسته منحنی ها و دسته منحنی های متعامد 5: معادله دیفرانسیل كامل 6:عامل انتگرال ساز 7: معادله دیفرانسیل مرتبه اول خطی و تبدیل به آن فصل دوم: معادله دیفرانسیل مرتبه دوم 1: معادله دیفرانسیل مرتبه دوم حالت خاص فاقد یا 2: معادله دیفرانسیل مرتبه دوم با ضرایب ثابت همگن 3: معادله دیفرانسیل کشی-اویلر 4: معادله دیفرانسیل مرتبه دوم خطی غیر همگن ( تغییر متغیر) 5: روش ضرایب ثابت( ضرایب نامعین) فصل سوم: حل معادله دیفرانسیل به روش سری ها 1: سری توانی 2: نقاط معمولی ومنفرد وجواب های سری معادلات دیفرانسیل 3: نقاط منفرد منظم معادلات دیفرانسیل خطی مرتبه دوم :4حالتی كه معادله شاخص دارای ریشه های برابر است فصل چهارم: 1:توابع بسل وخواص آن فصل پنجم 1: دستگاه معادلات دیفرانسیل فصل ششم: تبدیلات لاپلاس 1: تبدیل لاپلاس 2: خواص تبدیل لاپلاس 3: معکوس تبدیل لاپلاس 4: حل معادله دیفرانسیل به روش لاپلاس 5: تبدیل لاپلاس برخی توابع ماهیت معادله دیفرانسیل وطبقه بندی آن مقدمه: با مفهوم معادله یعنی رابطه ای که درآن تساوی باشد، آشنا هستیم. ساده ترین معادله یک مجهولی می باشد، که بانماد نشان f(x)=0 می دهیم. مثلا ax+b=0 معادله یک مجهولی درجه اول و ax^2+bx+c=0 معادله یک مجهولی درجه دوم و ax^3+bx^2+dx+c=0 معادله یک مجهولی درجه سوم والی آخر معادله دو مجهولی که بانماد f(x,y)=0 نشان می دهیم مثلا ax+by+c=0 معادله دو مجهولی درجه اول ax^2+bxy+cy^2+dx+ey+f=0 معادله دو مجهولی درجه دوم والی اخر درمورد معادله دونوع سوال قابل طرح می باشد: الف) آیا x0جواب معادله f(x)=0ميباشدويا(x0,y0) جواب معادله f(x,y)=0ميباشد ب) جواب معادله راپیدا کنید؟ جواب دادن به سوال الف) ساده می با شد زیرا با جایگذاری می توان مشخص کرد. ولی جواب دادن به سوال ب) مشکل می باشد. ابتدا باید معادلات را دسته بندی کرده وبرای هر نوع روش خاصی راارائه داده بعبارت دیگر برای حل معادله باید دو مرحله را مشخص کنیم: 1) مرحله شناخت 2) مرحله حل(روش حل) حال اگر درمعادله f(x,y)=0 متغیر x را به عنوان متغير مستقل ومتغير y را به عنوان متغیر وابسته درنظر بگیریم آن گاه ...
معادلات دیفرانسیل
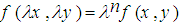
معادله دیفرانسیل همگن: تابع f(x,y) را همگن می گوییم هرگاه به ازای هر عدد ثابت رابطه ی زیر برقرار باشد: برای مثال تابع همگناز در جه ی اول می باشد: در معادله به فرم هرگاه p و Q توابعی همگن از یک درجه باشند معادله را همگن می گوییم.برای حل این نوع معادلات از تغییر متغیر زیر استفاده می کنیم: y=ux ==>dy=udx+xdu هرگاه معادله y’=f(x,y) همگن از درجه ی صفر باشد در چنین حالتی می توان f(x,y) را به فرم نوشت و با قرار دادن و y’=u’x+u معادله به یک معادله ی تفکیک پذیر تبدیل خواهد شد. معادلات دیفرانسیل کامل: معادله ی دیفرانسیل را کامل می گوییم هرگاه شرط برقرار باشد معادلات دیفرانسیل خطی مرتبه ی اول و مرتبه دوم معادله ی دیفرانسیلی که به فرم زیر نوشته شود و یا بتوان آن را به فرم زیر نوشتمعادله ی دیفرانسیل خطی می گویند: در صورتیکه q(x)=0 باشد معادله را همگن می گویند در غیر این صورت معادله غیر همگن است. جواب عمومی معادله ی دیفرانسیل غیر مگن خطی مرتبه ی اول به صورت زیر می باشد: معادلات دیفرانسیل خطی مرتبه دوم: صورت کلی معادلات دیفرانسیل خطی مرتبه دوم به صورت زیر می باشد: در اینجا هم اگر M(X)=0 باشد معادله همگن و در غیر اینصورت معادله غیر همگن می باشد. معادلات دیفرانسیل خطی مرتبه دوم همگن با ضرائب ثابت فرم کلی این نوع معادلات به صورت زیر می باشد: در رابطه ی بالا a و b اعداد ثابت متعلق به مجموعه اعداد حقیقی هستند.برای حل این معادلات,معادله ی مشخصه زیر را تشکیل می دهیم و بر حسب مقادیر که ریشه های معادله مشخصه است سه حالت خواهیم داشت: حالت اول:اگر معادله دارای دو ریشه ی حقیقی غیر مساوی و باشد,آنگاه جواب عمومی معادله به فرم زیر بیان خواهد شد و می گوییم جواب معادله همگن میرایی است: حالت دوم:اگر معادله دارای ریشه مضاعف باشد,آنگاه جواب عمومی معادله به صورت زیر بیان خواهد شد و می گوییم جواب معادله ی همگن میرایی بحرانی است: حالت سوم:در صورتیکه ریشه های معادله دو عدد مختلط باشند در این صورت جواب عمومی معادله به صورت زیر خواهد بود و می گوییم جواب های معادله نوسانی است.
دانلود حل المسائل معادلات دیفرانسیل مسعود نیکوکار
حل المسائل معادلات دیفرانسیل مسعود نیکوکارشما میتوانید برای اولین بار و تنها از این سایت با لینک مستقیم دانلود کنیدشامل :حل کلیه مسایل و معادلاتنکات وتمرینات اضافینمونه سوالات امتحانی حجم: ۳۹.۱ مگابایتفرمت :PDF دانلود
معادلات دیفرانسیل
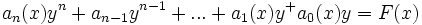
معادلات دیفرانسیل مقدمه نوع (عادی یا جزئی) مرتبه درجهساختار صور مختلف معادلات دیفرانسیل معادله دیفرانسیل همگن معادلات دیفرانسیل مرتبه دوم معادلات دیفرانسیل خطیحل معادلات دیفرانسیلی خطی مرتبه n ام به توسط سریهای توانی کاربردها مباحث مرتبط با عنوان مقدمه معادله دیفرانسیل معادلهای است که شامل یک یا چند مشتق یا دیفرانسیل باشد. معادلات دیفرانسیل بر اساس ویژگیهای زیر رده بندی میشوند: نوع (عادی یا جزئی) معادله شامل متغیر مستقل x ، تابع (y = f(x و مشتقات f را یک معادله دیفرانسیل عادی مینامیم. معادله ای متشکل از یک تابع مجهول با بیش از یک متغیر مستقل همراه با مشتقات جزئی آن معادله دیفرانسیل جزئی می نامیم. مرتبه که عباترت است از مرتبه مشتقی که بالاترین مرتبه را در معادله دارد. درجه نمای بالاترین توان مشتقی که بالاترین مرتبه را در معادله دارد، پس از حذف مخرج کسرها و رادیکالهای مربوط به متغیر وابسته و مشتقاتش. معمولا یک معادله دیفرانسیل مرتبه n جوابی شامل n ثابت دلخواه دارد، این جواب را جواب عمومی مینامند. ساختار معادلات دیفرانسیل ساختارهای متفاوتی هستند و هر ساختار ویژگیهای متفاوتی دارد: معادلات مرتبه اول از درجه اول با متغیرهای جدایی پذیر همگن خطی (برنولی) با دیفرانسیلهای کامل معادلات مرتبه دوم معادلات خطی با ضرایب ثابت: الف) همگن ب) ناهمگن. تکنیکهای تقریب زدن: الف) سریهای توانی ب) روشهای عددی. صور مختلف معادلات دیفرانسیل معادله دیفرانسیل مرتبه اول از درجه اول را همواره میتوان به صورت زیر در آورد که در آن M و N معرف توابعی از x و y هستند. Mdx + Ndy = 0در معادله فوق هرگاه M فقط تابعی از x و N فقط تابعی از y باشد. به صورت معادله جدایی پذیر مرتبه اول است. در این صورت با انتگرال گیری از هر جمله جواب بدست میآید. یعنی: M(x) dx+ ∫N(y) dy = C∫ معادله دیفرانسیل همگن گاه معادله دیفرانسیلی را که متغیرهایش جدایی پذیر نیستند با تعویض متغیر میتوان به معادلهای تبدیل کرد که متغیرهایش جدایی پذیر باشند، چنین معادلهای را همگن مینامند. معادله دیفرانسیل خطی مرتبه اول را همیشه میتوان به صورت متعارف زیر در آورد که در آن P و Q توابعی از x هستند. dy/dx + py = Qمعادله را که بتوان آن را به صورت: M (x,y) dx + N(x,y) dy = 0نوشت و دارای ویژگی زیر باشد کامل نامیده میشود. زیرا طرف چپ آن یک دیفرانسیل کامل است. M/∂y = ∂N/∂x∂ معادلات دیفرانسیل مرتبه دوم یک معادله دیفرانسیل مرتبه دوم در حالت کلی به صورت زیر است: F (x,y,dy/dx,d2y/dx2) = 0این گونه معادلات را معمولا با یک متغیر مناسب مثل dy/dx = p به معادلات دیفرانسیل نوع اول تبدیل کرد و با جاگذاری در معادله مربوط به ...
جزوه های معادلات دیفرانسیل
معادلات دیفرانسیل 1معادلات دیفرانسیل 2
معادلات دیفرانسیل
راهنمای معادلات دیفرانسیل دانلود کنید
