مطلب درباره ی طبیعت
هنر تجلیگاه ریاضیات
اسرار ازل را نه تو دانی و نه من وین حل معما نه تو دانی و نه من هست از پس پرده گفتگوی من و تو چون پرده بر افتد نه تو مانی و نه من مقدمه یکی از زیباترین دانش های بشری دانش ریاضیات است . از آنجا که علم ریاضی در پیشرفت سایر علوم بشری نقش عمدهای داشته و یکی از عوامل مهم توسعهی فنآوری در دهههای اخیر بوده است ، توجه بیشتر به آموزش همگانی آن در دنیای امروز ضروری به نظر می رسد . هرگاه کار روزانهتان ریاضیات باشد به نظرتان طبیعی ترین کار در دنیا می باشد .هر گاه کارتان را لحظهای متوقف کرده و فکر کنید که چکار می کنید و این کارها چه معنایی دارد ، به نظرتان ریاضیات یکی از اسرارآمیزترین امور است . چگونه قادریم از اشیایی سخن گوییم که هیچ کس هیچگاه آنها را ندیده است ، و در عین حال آنها را از اشیاء و ذوات ملموس زندگی روزمره بهتر بفهمیم ؟ هنر تجلیگاه ریاضیات ریاضیات و هنر دو علم جدایی ناپذیرند . جدایی از اینکه ریاضیات به عنوان مادر همه علوم می تواند در هر جایی توجیح قوانین را برعهده گیرد ، در هنر جلوهایی دیگر دارد بطوریکه عده زیادی از ریاضیدانان بزرگ قرن ریاضی را هنر ، هنرمند عالم می دانند نه هنر را ریاضی . هنر جلوه یا تجلیگاه زیبایی هاست . هنر هر چیزی است که احساس را نوازش می دهد . آیا یک ساختار ریاضی این خصوصیت را دارد ؟ ریاضی مجموعهای از مفاهیم اولیه است که تحت اصول خاصی با یکدیگر ارتباط دارند . زیبایی و هنر ریاضی بسیاری از افراد ریاضیات را دانش دشوار و دست نیافتنی می دانند و به همین مناسبت ، ریاضیدان و معلم ریاضی را فردی خشک و خشن ، عصبانی ، بی احساس و بی عاطفه می پندارند و از اینکه می بینند کسی که رشته اش ریاضیات است اهل ذوق و هنر و شعر و موسیقی باشد و از آن لذت ببرد ، متحیر می شوند . آیا می توان گفت هنر و ریاضیات متضاد و دور از هم و ناسازگارند ؟ ریاضیات در زندگی به چه دردی می خورد ؟ آیا علاقه به ریاضیات و تخصص داشتن در آن به معنای بی ذوقی و دور بودن از زندگی است ؟ هنر تعریف ریاضی باید جامع و مانع باشد هم چنانکه در یک نثر نیز این دو مورد باید رعایت شود همانطور که آوردن مطالب اضافی در نثر از زیبایی آن می کاهد در ریاضیات نیز مطالب اضافه ایجاد مشکل میکند. همانطور که در ریاضی مطالب با هم سازگارند در شعر نیز سازگاری از ارکان زیبایی به شمار می رود . هنر و ریاضیات همانند یکدیگرند . زیرا در هر دو تقارن ، تناظر و تطابق وجود دارد . به نظر من یکی از زیباترین و شیرین ترین درسهای دوران تحصیل تا انتها درس ریاضی می باشد . نقش هنر و زیبایی ریاضیات در زندگی روزمره ...
ریاضیات در آینهی اندیشهها
ریاضیات در آینهی اندیشهها - مطالب متنوع علمی و اخلاقی و تربیتی واطلاعات عمومی وتاریخی و آموزشی ریاضی - مطلب درباره ی ریاضی"> مطلب درباره ی ریاضی مطالب متنوع علمی و اخلاقی و تربیتی واطلاعات عمومی وتاریخی و آموزشی ریاضی صفحه اصلی | عناوین مطالب | تماس با من | قالب وبلاگ | پروفایل آخرين مطالب گفتگوی خواندنی با مهندس ایرانی ناسا/ بزودی به مشتری می رویم معمای مرد کور در جزیره معمای تصویری ستاره ی پنهان کاربرد تکنیک های حافظه برای حفظ سریع فرمول های ریاضی و مثلثاتی ـ معمای هر کسی چه کاره است؟؟؟ حل الگوریتم سیمون توسط یک رایانه کوانتومی برای نخستین بار بازخوانی دیدگاههای نویسنده عرب درباره علی (ع) و تشیع؛ تالیف کتاب های آموزش طبقه بندی شده ریاضی تالیف کتاب های کار ریاضی تالیف کتاب های گلبرگ ریاضی ( نمونه سوال های طبقه بندی شده ) لینک دوستان قالب بلاگفاقالب بلاگفا آنچه خود داشت ز بيگانه تمنا مي كرد... تا خدا هست جايي براي نااميدي نيست... آخرین انسان ، مقالات ادبی وشعر پیشرو بودن اسلام درفرهنگ وتمدن جهان درباره اسلام و ایران دانش آموز کوشا قالب میهن بلاگ Download لینک های مفید فروشگاه اینترنتی نمایش افراد آنلاین کد حدیث تصادفی فال حافظ تی ام دیزاین ریاضیات در آینهی اندیشهها ریاضیات در آینهی اندیشهها > ریاضیات شانه بر زلف پریشان عالم است . حسینالهیقمشهای > قوانین طبیعت ، تفکرات ریاضی خداوند هستند . اقلیدس > ریاضیات یعنی توانایی شمردن تا بیست ، بدون آنکه کفشهایمان را در بیاوریم . ناشناس > همزمان با گسترش دایرهی دانش ما، تاریکی اطراف این دایره نیز گستردهتر میشود . آلبرتانیشتین > همه میتوانند دانههای یک سیب را بشمارند، اما سیبهای یک دانه را نمیتوان شمرد . ناشناس > سختترین چیز در ریاضی وقتی است که بخواهیم نعمتهای خداوند را حساب کنیم . اریکهوفر > در ریاضیات به چیزهایی که سر در نمیآوری عادت میکنی . جاننیومن
تک درخت زیبا . . .

وبلاگ-کد لوگو و بنر شاندرمن ما ، شهر زيبايي هاي طبيعت اسلایدر تک درخت زیبا . . .
اندیشه های ریاضیدان ها
جورج پوليا: ریاضیات عبارت است از اثبات بدیهی ترین چیز به نابدیهی ترین روش ممکن.پواسون: زندگاني تنها به اين درد مي خورد كه انسان به دو كار مشغول گردد:اول: رياضي بخواند، دوم: رياضي درس بدهد.كيلي: در هر چيز از جمله يك نظريه رياضي زيبايي را ميتوان درك كرد اما نمي توان توضيح داد.ايمانوئل کانت: علم رياضي درخشان ترين مثال براي اين واقعيت است که چگونه استدلال محض دامنه تاثير گذاريش را بدون کمک تجربه گسترش مي دهد.پير فرما: و شايد آيندگان از اينکه نشان داده ام قديمي ها همه چيز را نمي دانستند، سپاسگزار من باشند.جان لاک: اثبات رياضي مانند الماس قاطع و شفاف است، و با چيزي جز استدلال دقيق نمي توان به آن رسيد.دمورگن: نيروي محرکه ابداع رياضي استدلال نيست، تخيل است.د.يا. سترويک: بايد به ياد داشته باشيد که مفهوم هاي رياضي نتيجه اي از کار آزاد ذهن نيستند بلکه انعکاسي از جهان واقعي و عيني دور وبر ما هستند که البته اغلب به صورت کاملا انتزاعي طرح مي شود.ب.فلدليوم: هر کشف تازه اي که در علوم طبيعي و صنعت رخ ميدهد تنها از راه به کار بردن نتيجه گيري هاي جديد در عمل و يا زنده کردن نظريه هاي فراموش شده رياضي است به اين ترتيب نظريه هاي رياضي از قبل راه پيشرفت علم وصنعت را پيش بيني مي کنند.هیلبرت: با وجود اهمیتی كه كاربرد ریاضیات دارد اما این كار نباید ملاك ارزش گذاری آن باشد. جینز: به نظر میرسد معمار بزرگ جهان ریاضیدان است. برتراند راسل: ریاضیات هیچ حقیقتی ندارد اما بالاترین زیبایی را داراست . یک زیبایی سرد و جدی، درست مانند یک تندیس ، به طور شگفت انگیزی محض ، و توانا در نهایت جدیت، به طوری که تنها بزرگترین هنرمندان می توانند این گونه باشند.گاوس: ریاضیات حاکم علوم است و نظریه اعداد ملکه ریاضیات.فیثاغورس: بدون ریاضیات شاید هنر و ادبیات داشته باشیم ولی تکنولوژی و صنعت هرگز چیزی در جهان وجود ندارد که با عدد قابل بیان نباشد. فیثاغورس: به کمک اعداد می توان زندگی و پیشامد های آن را پیش بینی کرد. هانری پوانکاره: دانشمند، طبیعت را به خاطر فایده اش مطالعه نمی کند، آن را برای این مطالعه می کند که از آن لذت می برد و چون طبیعت زیباست از آن لذت می برد. اگر طبیعت زیبا نبود، ارزش شناختن نداشت و اگر طبیعت ارزش شناختن نداشت، زندگی هم ارزش زیستن نداشت . البته، من در اینجا از آن گونه زیبایی که حواس را متأثر می کند، یعنی از زیبایی اوصاف و ظواهر، سخن نمی گویم؛ نه به این جهت که این زیبایی ها را دست کم بگیرم، نه چنین نیست، اما این زیبایی ربطی به علوم ندارد، منظورم زیبایی ژرف تری است که از نظم هماهنگ اجزا بوجود می آید و تنها هوش ناب قادر به درک ...
کوتاه وخواندنی تربیت کردن:
کوتاه وخواندنی تربیت کردن: تربیت کردن: تربیت کردن، مثل راه است، طی باید کرد. تربیت کردن، مثل مساله است حل باید کرد. تربیت کردن، تعهد است، عمل باید کرد. تربیت کردن، مثل باغبانی است، عشق باید ورزید. تربیت کردن، دراز مدت است، صبر باید کرد. تربیت کردن، دشوار است، تحمل باید کرد تربیت کردن، راز است، کشف باید کرد. تربیت کردن، هدیه است، قبول باید کرد. تربیت کردن، تفریح است، بازی باید کرد. تربیت کردن، مثل قالی بافتن است، گره باید زد. محروم نکنیم: طبیعت بهترین درسها را به بچه ها می دهد. ان ها را از طبیعت محروم نکنیم. دوستان، بهترین راه اجتماعی شدن را به فرزندانمان می اموزند، انها را از داشتن دوست محروم نکنیم. صحبت کردن در جمع، بهترین راه برای ابراز وجود است. بگذاریم فرزندانمان فرصت سخن گفتن در جمع را داشته باشند. کتاب، بهترین راهنما برای فرزندان است، ان ها را از ابتدای زندگی با کتاب اشنا کنیم. هنر، بهترین راه برای بیان خویشتن است. فرزندانمان را با هنرهای مختلف اشنا کنیم. استفاده از مطالب این وبلاگ با ذکر منبع بلا مانع است. http://www.daneshriazi.blogfa.com
مقاله تاریخچه ی ریاضیات
مقاله تاریخچه ی ریاضیات انسان اولیه نسبت به اعداد بیگانه بود و شمارش اشیاء اطراف خود را به حسب غریزه یعنی همانطور که مثلاً مرغ خانگی تعداد جوجههایش را میداند انجام میداد. اما بزودی مجبور شد وسیلة شمارش دقیقتری بوجود آورد. لذا، به کمک انگشتان دست دستگاه شماری پدید آورد که مبنای آن 60 بود. این دستگاه شمار که بسیار پیچیده میباشد قدیمیترین دستگاه شماری است که آثاری از آن در کهنترین مدارک موجود یعنی نوشتههای سومری مشاهده میشود. سومریها که تمدنشان مربوط به حدود هزار سال قبل از میلاد مسیح است در جنوب بینالنهرین، یعنی ناحیه بین دو رود دجله و فرات ساکن بودند. آنها در حدود 2500 سال قبل از میلاد با امپراطوری سامی، عکاد متحد شدند و امپراطوری و تمدن آشوری را پدید آوردند. در این موقع مصریها نیز در سواحل سفلای رود نیل تمدنی درخشان پدید آورده بودند. طغیان رود نیل هر سال حدود و ثغور زمینهای زراعتی این قوم را محو میکرد. احتیاج به تقسیم مجدد این اراضی موجب رهبری آنها به اولین احکام سادة هندسی گردید. همچنین مبادلات تجارتی و تعیین مقدار باج و خراج سالیانه آنها را وادار به توسعه علم حساب نمود این اطلاعات همگی از روی پاپیروسها و الواحی است که در نتیجه حفاریها بدست آمده و به خط هیروگلیفی میباشد. قدیمیترین آنها که مربوط به 1800 سال قبل از میلاد است شامل چند رساله دربارة علم حساب و مسائل حساب مقدماتی میباشد، از آن جمله رسالة پاپیروس آهس است که درسال 1868 توسط ایسنلر مصرشناس مشهور ترجمه شد. سایر تمدنهای شرقی نظیر چینی و هندی در ترویج دانش نقش مؤثری نداشتهاند و جز برخی نتایج پراکنده که در زیر فشار مفاهیم ماوراءالطبیعه خرد شده است چیزی از آنان در دست نیست. قریب هزار سال پس از نابودی فرهنگ قدیم مصر و محو تمدن آَشور، یونانیان از روی مقدمات پراکنده و بیشکل آنها علمی پدید آوردند که در واقع به عالیترین وجه مرتب و منظم گردیده و عقل و منطق را کاملاً اقناع مینمود. نخستین دانشمند معروف یونانی طالس ملطلی (639_548ق.م) است که در پیدایش علوم نقش مهمی بعهده داشته و میتوان ویرا موجد علوم فیزیک ، نجوم و هندسه «تشابه» به او کاملاً بیاساس است. در اوایل قرن ششم ق.م. فیثاغورث (572_500 قبل از میلاد) از اهالی ساموس یونان کمکم ریاضیات را بر پایه و اساسی قرار داد و به ایجاد مکتب فلسفی خویش همت گماشت. فیثاغورثیان عدد را بخاطر همآهنگی و نظمی که دارد اساس ومبدأ همه چیز میپنداشتند و بر این عقیده بودند که تمام مفاهیم را به کمک آن میتوان بیان نمود. پس از فیثاغورث باید از زنون فیلسوف و ریاضیدان یونانی که در 490ق.م در ایلیا متولد شده ...
ریاضیدان از دید دکتر الهی قمشه ای
ریاضیدان از دید دکتر الهی قمشه ای هر فرمول دانی که ریاضیدان نیست! ریاضیدان کسی است که فرمول ها را در همه جا تشخیص دهد، به عبارت دیگر مدل های ریاضی را در هر جایی بشناسد: در طبیعت، در اقتصاد، در فیزیک، در رفتار و ... . به قول شاعر: دیده ای خواهم که باشد شه شناس تا شناسد شاه را در هر لباسیکی از شگفتی های ریاضی این است که مثلاً اعداد نیوتن را در مثلثات می بینیم، در جبر هم می بینیم، در بسیاری از شاخه های ریاضی و در جایی که انتظار نداریم می بینیم و این یعنی وحدت.استفاده از مطالب این وبلاگ با ذکر منبع بلا مانع است. http://www.daneshriazi.blogfa.com
منشور در طبیعت
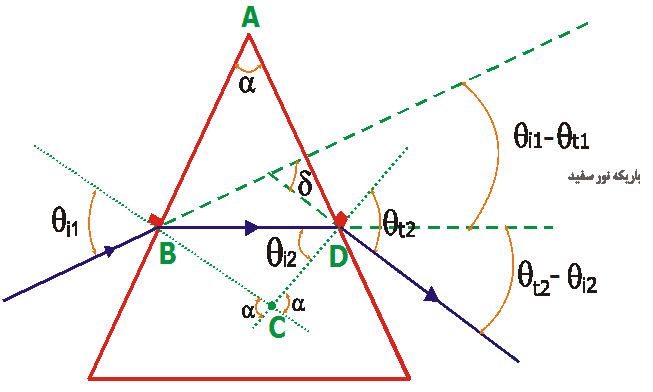
مثالی از کاربردمنشورها در طبیعت اگر وجود حشره ای می تواند ، با حل سریع یک مسئله ی هندسی ، ما را دچار شگفتی کند ، می توان به آ نچه که ساکنین کندوهای عسل ایجاد می کنند ، شاهکارهای ریاضی نامید . ساختمان شانه های کندو از یک رشته شبکه های مومی شش وجهی تشکیل شده اند که در دو قشر چیده شده اند و با کفهای مشترکی بهم مربوطند .عمق این شبکه 3/11 میلی متر ، عرض هر یک از شش دیواره ی شبکه مساوی 71/2 میلی متر و ضخامت آن مساوی ضخامت یک کاغذ نوشتنی معمولی است . بررسی این مطلب جالب است که چرا زنبور عسل برای مقطع منشور مومی خود ؛ شکل شش گوش را انتخاب کرده است ؟ این نتیجه ی تلاش مصرف کردن حداقل سطح در داخل یک گوشه ی تنگ است . قبل از همه باید چند ضلعی را به این شکل انتخاب کرد تا با تکرار آن بتوان سطح کندو را بدون هیچ فاصله و شکافی پوشانید. چه شکلهای منتظمی برای این منظورمناسبند ؟ ( البته این موضوع توسط فیثاغورث کشف شد ) این چند ضلعیها عبارتند از : مثلث ، مربع و شش ضلعی . به همین مناسبت زنبورهای هوشمند درباره ی چند ضلعیهای دیگر حتی فکر هم نکرده اند ؛زیرا در این صورت برای پر کردن سطح کندو می بایست از دو یا چند نوع مختلف شبکه استفاده کنند که مستلزم کار پیچیده تر و بیشتری بود . به این ترتیب آنها می توانستند از یکی از این سه نوع شکل استفاده کنند. و آنها از این سه حالت ممکن ، شش ضلعی را انتخاب کردند . چرا ؟ برای اینکه در بین این سه شکل ، وقتی که مساحتهای مساوی داشته باشند ،شش ضلعی کمترین محیط را دارد . یعنی وقتی که خانه ها را با قاعده ی شش ضلعی می سازند ، با حداقل مصرف موم ، حداکثر حجم رابدست می آورند منبع
نسبت طلائی
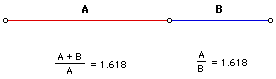
نسبت طلائی دنیای اعداد بسیار زیباست و شما می توانید در آن شگفتیهای بسیاری را بیابید. در میان اعداد برخی از آنها اهمیت فوق العاده ای دارند، یکی از این اعداد که سابقه آشنایی بشر با آن به هزاران سال پیش از میلاد میرسد عددی است بنام “نسبت طلایی” یا Golden Ratio. پاره خطی را در نظر بگیرید و فرض کنید که آنرا بگونه ای تقسیم کنید که نسبت بزرگ به کوچک معادل نسبت کل پاره خط به قسمت بزرگ باشد. به شکل توجه کنید. اگر این معادله ساده یعنی a2=a*b+b2 را حل کنیم (کافی است بجای b عدد یک قرار دهیم بعد a را بدست آوریم) به نسبتی معادل تقریبا” 1.61803399 یا 1.618 خواهیم رسید. شاید باور نکنید اما بسیاری از طراحان و معماران بزرگ برای طراحی محصولات خود امروز از این نسبت طلایی استفاده می کنند. چرا که بنظر میرسد ذهن انسان با این نسبت انس دارد و راحت تر آنرا می پذیرد. این نسبت نه تنها توسط معماران و مهندسان برای طراحی استفاده می شود بلکه در طبیعت نیز کاربردهای بسیاری دارد که به تدریج راجع به آن صحبت خواهیم کرد. اهرام مصر یکی از قدیمی ترین ساخته های بشری است که در آن هندسه و ریاضیات بکار رفته شده است. مجموعه اهرام Giza در مصر که قدمت آنها به بیش از 2500 سال پیش از میلاد می رسد یکی از شاهکارهای بشری است که در آن نسبت طلایی بکار رفته است. به این شکل نگاه کنید که در آن بزرگترین هرم از مجموعه اهرام Giza خیلی ساده کشیده شده است. مثلث قائم الزاویه ای که با نسبت های این هرم شکل گرفته شده باشد به مثلث قائم مصری یاEgyptian Triangle معروف هست و جالب اینجاست که بدانید نسبت وتر به ضلع هم کف هرم معادل با نسبت طلایی یعنی دقیقا” 1.61804 می باشد. این نسبت با عدد طلایی تنها در رقم پنجم اعشار اختلاف دارد یعنی چیزی حدود یک صد هزارم. باز توجه شما را به این نکته جلب می کنیم که اگر معادل فیثاغورث را برای این مثلث قائم الزاویه بنویسم به معادله ای مانند i2=phi+b2 خواهیم رسید که حاصل جواب آن همان عدد معروف طلایی خواهد بود. (معمولا” عدد طلایی را با phi نمایش می دهند ) طول وتر برای هرم واقعی حدود 356 متر و طول ضلع مربع قاعده حدودا” معادل 440 متر می باشد بنابر این نسبت 356 بر 220 (معادل نیم ضلع مربع) برابر با عدد 1.618 خواهد شد. کپلر (Johannes Kepler 1571-1630) منجم معروف نیز علاقه بسیاری به نسبت طلایی داشت بگونه ای که در یکی از کتابهای خود اینگونه نوشت : “هندسه دارای دو گنج بسیار با اهمیت می باشد که یکی از آنها قضیه فيثاغورث و دومی رابطه تقسیم یک پاره خط با نسبت طلايي می باشد. اولین گنج را می توان به طلا و دومی را به جواهر تشبیه کرد”. تحقیقاتی که کپلر راجع به مثلثی که اضلاع آن به نسبت اضلاع مثلث مصری باشد به حدی بود که امروزه ...
