مشتق لگاریتم
لگاریتم
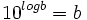
مقدمه در جبر عموما لگاریتم معمولی یا لگاریتم در پایه 10 عدد b را توانی تعریف میکنند که 10 باید به آن برسد تا b بدست آید: . فرض کنیم چنین عددی موجود بوده و از لگاریتمها برای سادهکردن ضرب اعدادی که ارقام اعشاری زیادی دارند استفاده میکنیم. تعریف تابع لگاریتم طبیعی بصورت زیر نمایش داده میشود: به ازای هر x بزرگتر از 1 ، این انتگرال مساحت ناحیهای را نشان میدهد که از بالا به خم از پایین به محور t از طرف چپ به خط t=1 ، و از طرف راست به خط t=x محدود است. تاریخچه در اواخر قرن شانزدهم یک بارون اسکاتلندی به نام جان نپر (1550-1617) ابزاری بنام لگاریتم ابداع کرد که با تبدیل ضرب به جمع کار محاسبه را ساده میکند؛ یعنی داریم: لگاریتم x + لگاریتم a = لگاریتم ax برای ضرب دو عدد مثبت x,a از یک جدول ، لگاریتمهای x,a را پیدا میکنیم، سپس این لگاریتمها را بهم میافزائیم مجموع حاصل را در داخل جدول مییابیم، و بالاخره حاصلضرب مطلوب ax را از حاشیه جدول میخوانیم. مسلما در دست داشتن جدول کلید کار بود، به همین سبب نپر در دو دهه آخر زندگیاش را صرف تهیه جدولی کرد که هیچگاه نتوانست آن را تمام کند. و این در حالی بود که تیکو براهه ستاره شناس ، مشتاقانه در انتظار این جدول بود تا میتواند محاسبات خودش را تسریع بخشد مشتق تابع لگاریتم طبیعی چون تابع با انتگرال ذکر شده در قسمت تعریف ، تعریف میشود، فورا از نخستین قضیه اساسی حساب دیفرانسیل و انتگرال نتیجه میشود که مشتق تابع برابر خواهد بود. بنابراین اگر u تابع مشتقپذیری از x باشد، آنگاه از قاعده زنجیری داریم: فرمول کلیتر زیر بدست میآید: مشتقگیری لگاریتمی گاهی یک تابع با معادلهای پیچیده داده شده با گرفتن لگاریتم از طرفین آن پیش از مشتقگیری میتوان مشتقش را سریعتر حساب کرد. خواص قلمرو: مجموعه تمام اعداد حقیقی مثبت ، x>0 برد: مجموعه تمام اعداد حقیقی این تابع بر قلمرو خود پیوسته و صعودی است هر گاه آنگاه . این تابع یک تابع یکبهیک از قلمرو خود به بردش است، بنابراین دارای معکوس است. حاصلضرب ، خارج قسمت و توان: هر گاه x,a دو عدد مثبت باشند. آنگاه:معکوس تابع لگاریتم چون یکبهیک و مشتقپذیر است، دارای معکوس مشتقپذیر میباشد نمودار منعکس نمودار تابع نسبت به خط y=x است. این نمودار تابع نیز میباشد. تابع به ازای هر عدد حقیقی x مساوی میباشد. تابع حاصل تابع مشتق پذیری از x است که به ازای هر x حقیقی تعریف شده است و بعنوان تابع نمایی از آن یاد میشود که e را پایه و x نما خوانده میشود. همچنین توجه میکنیم که حد تابع نمایی زمانی که x بسمت بینهایت میل میکند برابر بینهایت است و زمانی ...
تابع لگاریتمی
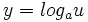
توابع لگاریتم در پایه محاسبه ی قواعد حاکم بر توابع لگاریتمیمشتق آهنگ های نسبی رشد توابع لگاریتم در پایه همچنین ببینید: توابع لگاریتم در پایه می دانیم که اگر عدد مثبتی به جز یک باشد، تابع مشتق پذیر و یک به یک است. علاوه بر این، مشتق آن یعنی ، هرگز صفر نمی شود. پس این تابع یک معکوس مشتق پذیر دارد که آن را " لگاریتم در پایه ی " نامیده و با نشان می دهند. چون و معکوس یکدیگرند، ترکیب آن ها به هر ترتیبی، تابع همانی است. پس روابط زیر به دست می آیند: بنابر این لگاریتم در پایه ی ، نمایی است که باید به توان آن برسد تا به دست آید. محاسبه ی عدد را همیشه میتوان به کمک فرمول زیر از لگاریتم های طبیعی و به دست آورد: این فرمول را می توان با روش زیر استنتاج کرد: قواعد حاکم بر توابع لگاریتمی الف)ب)ج) مشتق اگر تابع مشتق پذیری از باشد، آنگاه: چرا که: آهنگ های نسبی رشد توابع ممکن است توجه کرده باشید که توابع نمایی نظیر و ، وقتی بزرگ می شود، خیلی سریع تر از چند جمله ای ها و توابع گویا رشد می کنند. به ویژه این توابع نمایی خیلی سریع تر از تابع صعود خواهند کرد و وقتی زیاد می شود، بیش از فزونی می گیرد. در واقع وقتی ، توابع و تندتر از هر توان مثبتی از ، رشد می کنند. در مقابل، توابع لگاریتمی نظیر و ، که معکوس توابع و می باشند، وقتی ، از هر توان مثبتی از رشد کمتری دارند. به عنوان مثال اگر محور ها را با سانتیمتر مدرج کنیم، باید روی محور به اندازه ی چهار سال نوری جلو برویم تا نقطه ای بیابیم که به ازای آن ارتفاع نمودار تنها بشود. توجه: هر دو تابع لگاریتمی و ، وقتی ، با یک آهنگ رشد می کنند چرا که: و این حد همیشه متناهی و مخالف صفر است. لگاریتم در پایه لگاریتم های در پایه ، که غالبا " لگاریتم های معمولی " نامیده می شوند، در بسیاری از فرمول های علمی ظاهر می گردند. مثلا"، شدت زمین لرزه که بر حسب ریشتر گزارش می شود، دارای فرمولی به شرح زیر است: که در آن دامنه حرکت زمین بر حسب میکرون در ایستگاه گیرنده، دوره تناوب موج زلزله بر حسب ثانیه و ثابتی تجربی است که میزان تضعیف موج زلزله را با زیاد شدن فاصله از مرکز زمین لرزه نشان می دهد. یا مقیاس برای اندازه گیری قدرت اسیدی یک محلول، مقیاسی لگاریتمی است. مقدار ( یعنی پتانسیل هیدروژن ) محلول، لگاریتم طبیعی عکس غلظت یون هیدرونیم، است. نکته ای در مورد نماد گذاری: در بیشتر کتاب های درسی و ماشین حساب ها از ، برای نمایش استفاده می کنند. جدول انتگرال توابع لگاریتمی:
لگاریتم (2)

پیشینه پیشینیان ویراسنا، ریاضیدان هندی از کسانی بود که با مفهومی به نام ardhaccheda کار کرد. ardhaccheda یعنی تعداد دفعاتی که میتوان ۲n را نصف کرد. برای نمونه برای توانهای دقیق ۲ این کار برابر با لگاریتم گرفتن در مبنای ۲ بود؛ وی همچنین لگاریتم در پایهٔ دیگر اعداد صحیح مانند لگاریتم در پایهٔ ۳ (trakacheda) و در پایهٔ ۴ (caturthacheda) را نیز معرفی کرد.]مایکل استیفل در سال ۱۵۴۴ میلادی در نورنبرگ Arithmetica integra را منتشر کرد، در این نوشته جدولی از اعداد صحیح و توانهای ۲ داده شده بود، این جدول به عنوان نسخهٔ اولیهٔ جدول لگاریتم شمرده میشود. از نپر تا اویلر جان نپر (۱۶۱۷-۱۵۵۰) بدست آورندهٔ روش لگاریتمگیری روش لگاریتمگیری در سال ۱۶۱۴ از سوی جان نپر در کتابی با عنوان Mirifici Logarithmorum Canonis Descriptio (توصیفی بر قانون شگفتانگیز لگاریتم) ارائه شد.همچنین ژو بورجی (به فرانسوی: Joost Bürgi) نیز جداگانه روش لگاریتمگیری را پیدا کرده بود اما آن را شش سال پس از نپر منتشر کرد. نپر، با استفاده از روش تقسیمهای متوالی توانسته بود عبارت را به ازای Lهای میان ۱ تا ۱۰۰ محاسبه کند. جواب این عبارت برای ۱۰۰ = L تقریبا برابر است با ۰٫۹۹۹۹۹ = ۱ - ۵-۱۰ و ۲۰ ۰٫۹۹۵ ≈ ۰٫۹۹. این محاسبات که ۲۰ سال طول کشید، باعث شد تا او بتواند به ازای هر عدد N در بازهٔ ۵ تا ۱۰ میلیون، بتواند عدد L را پیدا کند که در رابطهٔ زیر صدق کند: نپر ابتدا نام «عدد ساختگی» را بر L نهاد ولی پس از مدتی واژهٔ «لگاریتم» logarithm را معرفی کرد و آن را بر عددی گذاشت که نمایندهٔ یک نسبت است: واژهٔ λόγος برابر logos به معنی «نسبت» است و واژهٔ ἀριθμός برابر arithmos به معنی «عدد» است. بوسیلهٔ عبارت زیر میتوان مفهوم پیشین لگاریتم را با مفهوم امروزی لگاریتم طبیعی مرتبط کرد: با تقریب خوبی داریم: این دستآورد خیلی زود مورد تحسین گستردهٔ دیگران قرار گرفت، به همین دلیل با تلاش دانشمندانی چون بوناونتورا کاوالیری (Bonaventura Cavalieri) از ایتالیا، ادموند ونگت (Edmund Wingate) از فرانسه، زو فنگزوئو (Xue Fengzuo) از چین و... مفهوم لگاریتم همه جا فراگیر شد. هذلولی y = ۱/x (منحنی قرمز) و سطح زیر آن از x = ۱ تا ۶ (قسمت نارنجی رنگ). در سال ۱۶۴۷ گرگوآر دو سن-ونسان توانست مفهوم لگاریتم را با یک چهارم هذلولی مرتبط کند، با فرض آنکه سظح زیر منحنی هذلولی به ازای ۱ = x تا t در رابطهٔ زیر صدق میکند: لگاریتم طبیعی اولین بار از سوی نیکولاس مرکاتور در مقالهٔ Logarithmotechnia که در سال ۱۶۶۸ منتشر کرد، توضیح داده شد. البته پیش از او جان اسپیدل که یک معلم ریاضی بود در سال ۱۶۱۹ جدولی از لگاریتم طبیعی را گردآوری کرده بود. در حدود سال ۱۷۳۰ لئونارد اویلر تابع نمایی ...
لگاريتم
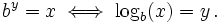
لگاریتم: یک عدد در یک پایه، توانی از پایه است که برابر آن عدد است. تابع لُگاريتم معکوس تابع نمایی است. به زبان ریاضی: با توجه به پایه لگاریتم، دو نامگذاری مختلف به کار میرود: لگاریتم طبیعی لگاریتم اعشاری اردادهای نوشتاری ریاضیدانان عموماً هر دوی(log(x یا(ln (x را به معنای(log(x یعنی لگاریتم طبیعی x بکار میبرند و مینویسند«log10(x)»،اگر پایه 10 لگاریتم x خواسته شده باشد، گرچه اغلب در ایالات متحده(log(x و یا(log (xy بدون پایهای مشخص بکار میرود، به معنای«log10(x)». ـ مهندسین زیستشناسان و برخی دیگر فقط ln(x) مینویسند (یا بعضی اوقات ) زمانی که لگاریتم طبیعی x را میخواهند و به کار میبرند “(log(x «برای (به معنی) »log10(x)«. یاًlog2(x)». ـ در بیشتر اوقات، زبانهای برنامهنویسی که متداولاً استفاده میشود cft , c و فرتون و بیسیک منظور از log یا LOG، لگاریتم طبیعی است. ـ در ماشینحسابهای دستی، لگاریتم طبیعی مشخص شدهاست با ln در حالیکه منظور از log، پایه 10 لگاریتم است. دلایل طبیعی بودن اصولاً به نظر میآید که در جهان پایه 10 برای تقریباً همهجا و محاسبات، استفاده میشود، این پایه بیشتر خواسته میشود، نسبت به پایه e. به دو دلیل ما(ln(x را طبیعی مینامیم. اول: تعبیر اینکه متغیرهای ناشناختهای که ظاهر میشود به عنوان توانی از e، بیشتر وجود دارند نسبت به توانها 10، و دوم: لگاریتم طبیعی نسبتاً آسانتر از یک انتگرال ساده یا سری تیلور میتواند تعریف شود. چیز یکه در مورد لگاریتمهای دیکر درست نیست، بنابراین لگاریتم طبیعی مفیدتر است در ادامه عیناً دیده خواهد شد در تمرینات. مسئله از مشتق گرفتن یک تابع لگاریتمی را ملاحظه کنید. اگر پایهٔ b مساوی با e باشد مشتق 1/x و در 1=x شیب نمودار 1 است. دلایل دیگر برای طبیعی بودن لگاریتم طبیعی وجود دارد. تعداد زیادی از سریهای ساده وجود دارند که شامل لگاریتمهای طبیعیاند و این اغلب در طبیعت رخ میدهد، در حقیقت نیکولاس هرکاتر، توصیفکننده آنها به عنوان طبیعتگیرای log تا قبل از حساب دیفرانسیل انتگرال تصور شدهاست. تعاریف (ln(x صریحاً ممکن است به عنوان ناحیهٔ زیر نمودار (انتگرال) 1/x از 1 تا a تعریف شود و آن این است این تعریف یک لگاریتم است چون خاصیت بنیادی لگاریتم را ایفا میکند این رابطه با جایگذاری چنان که در زیر آمده، میتواند اثبات شود رقم e میتواند یک عدد حقیقی یکتا a تعریف شود، بطوری که 1=(ln(a متناوباً: اگر یک تابع نمایی تعریف شده باشد نخست یک سری نامتناهی استفاده میشود. لگاریتم طبیعی ممکن است به عنوان تابع معکوس آن تعریف شود؛ یعنی (ln(x تابعی است که . از این رو برد توابع نمایی در مباحث حقیقی، تمام اعداد ...
لگاریتم طبیعی
قراردادهای نوشتاری ریاضیدانان عموماً هر دوی(log(x یا(ln (x را به معنای(log(x یعنی لگاریتم طبیعی x بکار میبرند و مینویسند«log10(x)»،اگر پایه 10 لگاریتم x خواسته شده باشد، گرچه اغلب در ایالات متحده(log(x و یا(log (xy بدون پایهای مشخص بکار میرود، به معنای«log10(x)». ـ مهندسین زیستشناسان و برخی دیگر فقط ln(x) مینویسند (یا بعضی اوقات ) زمانی که لگاریتم طبیعی x را میخواهند و به کار میبرند “(log(x «برای (به معنی) »log10(x)«. یاًlog2(x)». ـ در بیشتر اوقات، زبانهای برنامهنویسی که متداولاً استفاده میشود cft , c و فرتون و بیسیک منظور از log یا LOG، لگاریتم طبیعی است. ـ در ماشینحسابهای دستی، لگاریتم طبیعی مشخص شدهاست با ln در حالیکه منظور از log، پایه 10 لگاریتم است. دلایل طبیعی بودن اصولاً به نظر میآید که در جهان پایه 10 برای تقریباً همهجا و محاسبات، استفاده میشود، این پایه بیشتر خواسته میشود، نسبت به پایه e. به دو دلیل ما(ln(x را طبیعی مینامیم. اول: تعبیر اینکه متغیرهای ناشناختهای که ظاهر میشود به عنوان توانی از e، بیشتر وجود دارند نسبت به توانها 10، و دوم: لگاریتم طبیعی نسبتاً آسانتر از یک انتگرال ساده یا سری تیلور میتواند تعریف شود. چیز یکه در مورد لگاریتمهای دیکر درست نیست، بنابراین لگاریتم طبیعی مفیدتر است در ادامه عیناً دیده خواهد شد در تمرینات. مسئله از مشتق گرفتن یک تابع لگاریتمی را ملاحظه کنید. اگر پایهٔ b مساوی با e باشد مشتق 1/x و در 1=x شیب نمودار 1 است. دلایل دیگر برای طبیعی بودن لگاریتم طبیعی وجود دارد. تعداد زیادی از سریهای ساده وجود دارند که شامل لگاریتمهای طبیعیاند و این اغلب در طبیعت رخ میدهد، در حقیقت نیکولاس هرکاتر، توصیفکننده آنها به عنوان طبیعتگیرای log تا قبل از حساب دیفرانسیل انتگرال تصور شدهاست. تعاریف (ln(x صریحاً ممکن است به عنوان ناحیهٔ زیر نمودار (انتگرال) 1/x از 1 تا a تعریف شود و آن این است این تعریف یک لگاریتم است چون خاصیت بنیادی لگاریتم را ایفا میکند این رابطه با جایگذاری چنان که در زیر آمده، میتواند اثبات شود رقم e میتواند یک عدد حقیقی یکتا a تعریف شود، بطوری که 1=(ln(a متناوباً: اگر یک تابع نمایی تعریف شده باشد نخست یک سری نامتناهی استفاده میشود. لگاریتم طبیعی ممکن است به عنوان تابع معکوس آن تعریف شود؛ یعنی (ln(x تابعی است که . از این رو برد توابع نمایی در مباحث حقیقی، تمام اعداد حقیقی مثبت است. و از این رو تابع نمایی اکیداً صعودی است. این یک مشخصه برای همه اعداد مثبت x است. مشتق، سری تیلور و مباحث مختلط مشتق لگاریتمهای طبیعی به وسیلهٔ گرفته میشود، این به سری تیلور منتهی ...
عدد نپر
نظریه ها و قاعده های ریاضی با کشف خود "هستی"پیدا میکنند.ان ها تنها وجود دارند و اغلب بدون کاربردند.دیر یا زود و گاهی بعد از صدها و هزارها سال این موجودات ریاضی به "صفت"تبدیل میشوند و کاربرد خود را در زندگی و عمل در سایر دانش ها و در صنعت و هنر پیدا می کنند. "اویلر" عدد نپر...e=2.7182818284590452353602874713527 است.پرکاربردترین عدد گنگی که بشر تا بحال کشف کرده عدد نپر است.کشف این عدد منتسب به جان نپر((John Napierدانشمند اسکاتلندی و معرف لگاریتم است. البته اهمیت این عدد بیشتر مرهون کارهای لئونارد اویلر (Leonhard Euler)دانشمند سوئیسی است. چه بسیاری نیز معتقدند انتخاب حرف eبرای عدد نپر بخاطر اولین حرف از نام خانوادگی اویلر بوده;همینطور گفته می شود کاشف عددeان گونه که برخی می پندارند اویلر نبوده است بلکه خود نپر بحث مربوط به لگاریتم طبیعی و عددeرا در یکی از نوشته هایش پیش کشیده است.البته عده ای نیز می گویند این حرف نخستین حرف کلمه نمایی(exponential)است. در واقع توابع نمایی بصورت f(x)=a^xهستند و در بین تمام اعداد حقیقی ممکنی که می توانند بجای aقرار گیرند عدد نپر تنها عددیست که باعث می شود تابع نمایی در نقطه صفر دقیقا شیبی برابر یک داشته باشد(مشتق تابع e^xبرابر است با e^x و لذا شیب این تابع در صفر برابر است با e^0=1). تعاریف مختلف عدد نپر اگر,a>0,a=!1انگاه f(x)=a^x تابعی پیوسته با قلمرو Rو بردR+است.به ویزه برای تمام xها,a^x>0 .اگر 01 تابعی صعودی است و از انجا که هر تابع نزولی و هر تابع صعودی یک به یک هستند بنابراینf(x)دارای تابع وارون 1- f است که تابع لگاریتمی در پایه aنامیده می شود. و بوسیله log a نشان داده می شود. که با فرمولبندی تابع وارون: (x)=y ó f(y)=x^a 1- f Log ax=y ó a^y=x از تمام پایه های ممکن برای لگاریتم ها,انتخاب پایه e بیشترین سهولت را ایجاد می کند.لگاریتم در پایه e لگاریتم طبیعی نامیده میشود و دارای نماد خاص زیر است : Logex=ln x (نماد دیگری که گاهی بکار میرودxe log=log x یعنی پایه ان حذف مب شود زیرا eرایج ترین پایه مورد استفاده می باشد.) لگاریتم طبیعی را می توان برای همه اعداد حقیقی مثبت x که در زیر ناحیه زیر منحنی y=1/x از 1تا a تعریف نمود و همچنین برای اعداد مختلط غیر صفر می توان تعریف کرد. تابع لگاریتم طبیعی همچنین به عنوان تابع معکوس تابع نمایی که منجر به همانی می شود می توانیم تعریف کنیم. e^ln(x)=x if x>0 ln(e^x)=x. به بیان دیگر تابع لگاریتم یک نگاشت دو سویی است از مجموعه اعداد حقیقی مثبت به مجموعه همه ...
توابع نمایی در ریاضی
کشف لگاریتم: مقدمه نظريه ها و قاعده هاي رياضي، با کشف خود «هستي» پيدا مي کنند، آن ها تنها وجود دارند و اغلب بدون کاربردند. دير يا زود، و گاهي بعد از صدها و هزارها سال، اين موجودات رياضي به «صفت» تبديل مي شوند و کاربرد خود را در زندگي و عمل، در ساير دانش ها، در صنعت و هنر پيدا مي کنند. «اويلر» شايد کسي فکر نمي کرد لگاريتمي که در رابطه با نياز محاسبات عملي کشف شد در آينده کاربردهاي وسيعي پيدا کند. با ورود لگاريتم به دنياي رياضيات و آشنا شدن مردم و دانشمندان با آن، اين شاخه کاربردهاي زيادي را در زندگي روزمره پيدا کرد. چنانکه امروزه لگاريتم در حسابداري و در تعيين بهره ي مرکب و نيز مسائل مالي کاربرد فراواني يافته است. همان زمان که لگاريتم اختراع شده بود اويلر رابطه ي بين عدد e و بهره ي مرکب را دريافت و فهميد که حد بهره به سمت عددي متناسب (يا مساوي در شرايط خاص) ، که همان عدد e است ميل مي کند. همچنين از لگاريتم در مدلسازي و بازار يابي سهمي استفاده مي شود. مدلسازي ايجاد الگو و تمثيلي براي تجسم واقعيت هاي خارجي است که در مسائل مربوط به رياضيات و حسابداري کاربرد دارد لگاريتم به توان رساندن داراي 2 عمل معکوس مي باشد. اگر a=c در اين صورت پيدا نمودن a يعني استخراج ريشه يکي از دو عمل معکوس مي باشد و پيدا نمودن b يعني لگاريتم گيري عمل معکوس ديگر است. لگاريتم به چه منظوري اختراع شده است؟ بديهي است که تا نياز به چيزي احساس نشود آن چيز کشف و اختراع نمي گردد، در واقع هرکدام از علومي که با آن روبه رو هستيم هريک به مقتضاي نيازي و با توجه به هدف خاصي پيکر بندي شده اند. لگاريتم نيز با توجه به محاسبه هاي طولاني و ملال آوري که دانشمندان سده هاي شانزدهم و هفدهم ميلادي با آن سر و کار داشتند، بوجود آمد. اين محاسبه ها وقت و نيروي زيادي را از دانشمندان تلف مي کرد و هميشه دانشمندان در ذهن داشتند که چطور مي شود بدون انجام چنين محاسبات پيچيده و دشواري و آن هم در کمترين زمان ممکن به جواب مطلوب دست يابند. گفته مي شود که حتي در قرن هشتم هندي ها با محاسبات مربوط به لگاريتم آشنايي داشتند اما اين کلمه و مفهوم مربوط مي شود به قرن شانزدهم .جدول هايي نيز در اين زمينه بوجود آمد و شايد همين تلاش ها و نيازها بود که سر انجام به کشف لگاريتم انجاميد تا آن جا که دو دانشمند به طور همزمان و بدون اينکه از کار يکديگر آگاه باشند موفق به کسب چنين افتخاري گشتند اولي جان نپر و ديگري بورگي. اما اصطلاح لگاريتم نشات گرفته از فعاليت هاي نپر است که از واژه ي يوناني «لوگوس» به معني نسبت و «ارتيوس» به معني عدد گرفته شده است. او همچنين بجاي لگاريتم از اصطلاح عدد ساختگي ...
