مساحت بیضی
مساحت ، محیط و حجم شکلهای هندسی
مساحت مثلث با معلوم بودن سه ضلع آن برابرحاصل جذر (( p× ( p -a) × (p - b) × (p-c ) است که در آن p نصف محیط مثلث است وa,b,c ضلعهای مثلث هستند. مساحت مثلث برابراست با: نصف حاصلضرب يك قاعده در ارتفاع نظيرش مساحت متوازی الاضلاع برابر است با: حاصلضرب يك قاعده در ارتفاع مساحت مستطیل برابر است با : طول × عرض مساحت لوزی برابر است با : نصف حاصلضرب دو قطر مساحت مربع برابراست با : حاصلضرب یک ضلع در خودش ( يا مجذور يك ضلع ) مساحت ذوزنقه برابر است با: 2÷ ( حاصل جمع دو قاعده × ارتفاع ) محیط چندضلعی ها بالا برابر است حاصل جمع اندازه ی ضلع های آنها مساحت دایره برابر است با : شعاع× شعاع × ۱۴/۳ محیط دایره برابر است با : قطر × ۱۴/۳ مساحت بیضی برابر است با : نصف قطر بزرگ × نصف قطر کوچک × ۱۴/۳ مساحت کره برابر : شعاع × شعاع × ۱۴/۳× 4 حجم کره برابر : 3 ÷ ( شعاع × شعاع × شعاع × ۱۴/۳× 4 ) حجم استوانه برابر است با : مساحت قاعده × ارتفاع یعنی ( شعاع × شعاع × ارتفاع × ۱۴/۳ ) مساحت بدنه ( سطح جانبی )استوانه برابر : ارتفاع× ۱۴/۳× قطر حجم منشور برابراست با: مساحت قاعده × ارتفاع مساحت بدنه ( سطح جانبی ) منشور برابر :محیطقاعده× ارتفاع حجم هرم برابر است با: 3 ÷(مساحت قاعده × ارتفاع ) حجم مخروط برابر است با: 3÷ (مساحت قاعده × ارتفاع ) حجم مکعب مستطیل برابر : طول× عرض× ارتفاع
بیضی کیست ؟؟؟ چیست ؟؟؟ مساحتش چیست ؟؟؟
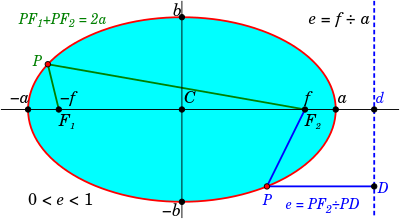
در هندسه، یک بیضی یک خم مسطح (خمی که در یک صفحهٔ اقلیدوسی تشکیل شدهاست.) است که از برخورد یک صفحه با یک مخروط ایجاد میشود به شرطی که خم ایجاد شده بسته باشد. برابر انگلیسی واژهٔ بیضی، ellipse از واژهٔ یونانی ἔλλειψις elleipsis به معنی falling short گرفته شدهاست. دایره حالت خاص بیضی است؛ که هنگامی بدست میآید که صفحهٔ عمود بر محور مخروط با آن برخورد کرده باشد. تعریف دیگر بیضی عبارت است از: مکان هندسی نقاطی از صفحهاست که مجموع فاصلههای آنها از دو نقطهٔ ثابت به یک اندازه ثابت مثبت باشد. بیضیها خمهای بسته و محدود از مقطع مخروط اند، این خمها از برخورد یک مخروط دایرهای با یک صفحه که از رأس مخروط نمیگذرد تشکیل شدهاند. دو نوع خم دیگر نیز از برخورد صفحه با مخروط میتوانند ایجاد شوند، این خمها همگی باز اند و تشکیل سهمی و هذلولی میدهند. در تعریفی دیگر بیضی مکان هندسی نقاطی است که نسبت فاصله آن از یک نقطه (کانون بیضی)، به فاصله آن از یک خط (خط هادی) برابر با عددی ثابت و کوچکتر از یک است. اجزای بیضی یک بیضی و برخی ویژگیهای ریاضی آن. یک بیضی یک خم بستهاست که نسبت به محورهای عمودی و افقی خود متقارن است. دو نقطه بر روی محیط بیضی که در دو سوی مخالف هم قرار دارند، یا به بیان دیگر، دو نقطه که خط واصل میان آنها از مرکز بیضی عبور میکند هنگامی در دورترین فاصله نسبت به هم قرار دارند که بر روی قطر بزرگ بیضی یا محور تقارن بزرگتر بیضی قرار گرفته باشند؛ و هنگامی کمترین مقدار را دارد که آن دو نقطه بر روی محور عمود بر قطر بزرگ، یعنی محور تقارن کوچکتر یا قطر کوچک بیضی قرار گرفته باشند.[۱] نیمقطر بزرگ (که در شکل با a نمایش داده شدهاست) و نیمقطر کوچک بیضی (که در شکل با b نمایش داده شدهاست) به ترتیب نیمی از قطر بزرگ و نیمی از قطر کوچک بیضی اند که گاهی به آنها شعاع کوچک (major radius) و شعاع بزرگ (minor radius) نیز میگویند. همچنین در انگلیسی به آنها major semi-axes و minor semi-axes نیز گفته میشود. محیط بیضی محیط بیضی به کمک انتگرالهای کامل بیضوی نوع دوم قابل محاسبهاست. البته فرمول صریحی همانند مساحت بیضی که برابر A = πab میباشد برای محیط بیضی وجود ندارد. و محیط بیضی تنها بوسیلهٔ سری نامتناهی قابل محاسبهاست: یا در روابط فوق ε خروج از مرکز بیضی است. در ضمن خروج از مرکزیت بیضی برابر با فاصلهٔ دو کانون تقسیم بر قطر اطول(2a) میباشد.حروف مرتبط : بیضی / اولین فرمول مساحت بیضی / مساحت بیضی / بیضی چیست / انتگرال بیضی / محیط بیضی /
حجم ومساحت اشکال هندسی /ریاضی ششم
دانش آموزان عزیز :در ایام تعطیلات نوروز با مطالعه و تمرین بخش مساحت و حجم به اطلاعات خود در این زمینه بیفزایید حجم:(Volume) حجم در لغت به معنی برآمدگی و ستبری و جسامت چیزی می باشد و در اصطلاح هندسه گنجایش و ظرفیت جسم و آن مقداری از فضا که جسم آن را اشغال می کند, را نشان می دهد. منشور: (Prism) منشور در لغت به معنی پراکنده, نشر شده, زنده شده و مبعوث است و در اصطلاح هندسه نام شکلی است که دو قاعده دارد که دو چند ضلعی مساوی هستند و بدنه منشور(سطح جانبی منشور ) از مستطیلها یا متوازی الاضلاع ها تشکیل شده است. معرفی منشور 5 پهلو: í نام شکل: منشور 5 پهلو í یال های منشور: 'EE',DD',CC',BB',AA í وجه منشور: هر کدام از مستطیل های جانبی را یک وجه منشور می نامند. í ارتفاع منشور: از آنجا که هر کدام از یال ها بر دو قاعده منشور عمود می باشند, لذا ارتفاع منشور با اندازه هر یک از یال ها برابر است. í قاعده ی منشور: منشور دو قاعده دارد. ABCDE و 'A'B'C'D'E که دو پنج ضلعی مساوی اند. رابطه های مهم: ارتفاع × مساحت قاعده = حجم منشور ارتفاع × محیط قاعده = مساحت جانبی منشور مساحت دو قاعده + مساحت جانبی = مساحت کل منشور استوانه: (Cylinder) نام شکلی است که دو قاعده دارد که دو دایره مساوی هستند و بر جانبی راست استوار است. اگر مستطیل را حول طول آن دوران دهیم, شکل فضایی حاصل استوانه نامیده می شود. در این صورت طول مستطیل ارتفاع استوانه و عرض آن شعاع قاعده استوانه می باشد. در شکل بالا مستطیل ABCD را حول طول آن دوران داده ایم و استوانه بوجود آمده است. رابطه های مهم: ارتفاع×مساحت قاعده(دایره) = حجم استوانه ارتفاع×محیط قاعده(دایره) = مساحت جانبی استوانه مساحت دو قاعده + مساحت جانبی = مساحت کل استوانه هرم: (pyramid) هرم در لغت به معنی سخت پیر گردیدن و کلان سال شدن است و در اصطلاح هندسه حجمی است که قاعده آن یک چند ضلعی و وجوه جانبی اش مثلثهایی باشند که همه به یک رأس مشترک(رأس هرم) منتهی می شوند. معرفی هرم منتظم: í نام شکل: هرم منتظم. í رأس هرم: نقطه S í ارتفاع هرم: پاره خطی است که از رأس هرم به مرکز قاعده ی هرم عمود است(SO) í قاعده هرم: پنج ضلعی منتظم ABCDE í سهم هرم: ارتفاع مثلث های جانبی, ارتفاع هر وجه جانبی هرم منتظم(SH). í وجه هرم: هر یک از مثلث هایی که بدنه هرم را می پوشانند را یک وجه جانبی می نامیم. í یال هرم: محل تقاطع هر دو وجه جانبی را یال هرم می نامیم. SE,SD,SC,SB,SA رابطه های مهم: مخروط : (cone) مخروط به معنی خراشیده شده ، تراشیده شده و خراطی شده است ودر اصطلاح هندسه حجمی است که از دوران مثلث قائم الزاویه حول یک ضلع آن به دست می آید . کله قند و کلاه بوقی ...
مساحت ، محیط و حجم شکل های هندسی
مساحت مثلث با معلوم بودن سه ضلع آن برابرحاصل جذر p× (p-a) × (p-b) × (p-c)است که در آن p نصف محیط مثلث است وa,b,c ضلعهای مثلث هستند. مساحت مثلث برابراست با: نصف حاصلضرب قاعده در ارتفاع مساحت متوازی الاضلاع برابر است با: حاصلضرب قاعده در ارتفاع مساحت مستطیل برابر است با : طول × عرض مساحت لوزی برابر است با : نصف حاصلضرب دو قطر مساحت مربع برابراست با : حاصلضرب یک ضلع در خودش مساحت ذوزنقه برابر است با: 2÷ ( حاصل جمع دو قاعده × ارتفاع ) محیط چندضلعی ها بالا برابر است حاصل جمع اندازه ی ضلع های آنها مساحت دایره برابر است با : شعاع× شعاع × 14/3 محیط دایره برابر است با : قطر × 14/3 مساحت بیضی برابر است با : نصف قطر بزرگ × نصف قطر کوچک × 14/3 مساحت کره برابر : شعاع × شعاع × 14/3× 4 حجم کره برابر : 3 ÷ ( شعاع × شعاع × شعاع × 14/3× 4 ) حجم استوانه برابر است با : مساحت قاعده × ارتفاع یعنی ( شعاع × شعاع × ارتفاع × 14/3 ) مساحت بدنه ( سطح جانبی )استوانه برابر : ارتفاع× 14/3× قطر حجم منشور برابراست با: مساحت قاعده × ارتفاع مساحت بدنه ( سطح جانبی ) منشور برابر :محیطقاعده× ارتفاع حجم هرم برابر است با: 3 ÷(مساحت قاعده × ارتفاع ) حجم مخروط برابر است با: 3÷ (مساحت قاعده × ارتفاع ) حجم مکعب مستطیل برابر : طول× عرض× ارتفاع فرمول های ریاضی یک ضلع × خودش = مساحت مربع یک ضلع × 4 = محیط مربع طول × عرض = مساحت مستطیل 2× (طول + عرض) = محیط مستطیل 2 ÷ (قاعده × ارتفاع) = مساحت مثلث مجموع سه ضلع = محیط مثلث نصف ارتفاع × (قاعده بزرگ + قاعده کوچک) = مساحت ذوزنقه مجموع 4 ضلع = محیط ذوزنقه 2÷ (قطر بزرگ × قطر کوچک) = مساحت لوزی یک ضلع × 4 = محیط لوزی ارتفاع × قاعده = مساحت متوازی الاضلاع مجموع دو ضلع متوالی × 2 = محیط متوازی الاضلاع عدد پی × مجذور شعاع = مساحت دایره 14/3 × شعاع × شعاع 14/3 × قطر = محیط دایره مساحت کره چهار ×عدد پی × مجذور شعاع = مساحت کره حجم کره عدد پی × شعاع به توان 3 = حجم کره 14/3 × (نصف قطر کوچک × نصف قطر بزرگ) = مساحت بیضی یک ضلع × تعداد اضلاع = محیط چند ضلعی منتظم طول یال × مساحت یک وجه = حجم مکعب ارتفاع × عرض × طول = حجم مکعب مستطیل ارتفاع × قاعده = حجم مکعب ارتفاع هرم × مساحت قاعده هرم = حجم هرم ارتفاع × مساحت قاعده = حجم استوانه ارتفاع × محیط قاعده = مساحت جانبی سطح دو قاعده + مساحت جانبی = سطح کل استوانه مجموع ...
محیط و مساحت اشکال هندسی

مساحت مـــربع = یـــک ضلع × خـــودش محیــط مـــربــــع = یک ضلع × 42) مساحت مسـتطیـــــــل = طـول × عـرض محیط مستطیل = ( طول + عرض) × 23) مساحت مثلث = ( قاعده × ارتــــــفاع ) ÷ 2 محیط مثلث = مجموع سه ضلع4) مساحت مثلث متساوی الاضلاع = ( قاعده × ارتفاع ) ÷ 2 محیط مثلث متساوی الاضلاع = یک ضلع × 35) مساحت مثلث متساوی الساقین = ( قاعده × ارتفاع ) ÷ 2 محیط مثلث متساوی الساقین= مجموع سه ضلع6) مساحت مثلث قائم الزاویه = ( قاعده × ارتفاع ) ÷ 2 محیط مثلث قائم الزاویه = مجموع سه ضلع7) مساحت ذوزنقه = ( قاعده بزرگ + قاعده کوچک ) × نصف ارتفاع محیط ذوزنقه = مجموع چهار ضلع8) مساحت لوزی = ( قطر بزرگ × قطر کوچک ) ÷ 2 محیط لوزی = یک ضلع × 49) مساحت متوازی الاضلاع = قاعده × ارتفاع محیط متوازی الاضلاع = مجموع دو ضلع متوالی × 210) مساحت دایره = عدد پی ( 14/3 ) × شعاع × شعاع محیط دایره = عدد پی ( 14/3 ) × قطر11) مساحت کره = 4 × 14/3 × شعاع به توان دو حجم کره = چهار سوم × 14/3 × شعاع به توان سه12) مساحت بیضی = (نصف قطر بزرگ × نصف قطر کوچک ) × 14/3 13 ) محیط چند ضلعی منتظم = یک ضلع × تعداد اضلاعش14 ) حجم مکعب مستطیل = طـول × عـرض × ارتفاع حجم مکعب مربع = قاعده × ارتفاع ( طول یال×مساحت یک وجه)15 ) حجم هرم = مساحت قاعده ی هرم × ارتفاع هرم× یک سوم 16) مساحت جانبی استوانه = محیط قاعده × ارتفاع حجم استوانه = مساحت قاعده × ارتفاعسطح کل استوانه = سطح دو قاعده + مساحت جانبی ( مساحت مجموع دو قاعده + ارتفاع × پیرامون قاعده )17) مساحت جانبی منشور = مجموع مساحت سطوح جانبی مساحت کلی منشور = مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی18) حجم مخروط = مساحت قاعده × یک سوم × ارتفاع
محیط و مساحت بیضی
به دنبال مساحت و محیط بیضی هر چی توی اینترنت گشتم چیزی ندیدم ولی یادم افتاد که یه زمانی درسش رو تو کتاب محاسبات فنی دوره هنرستان خوندیم.... با مراجعه به کتابای سالای قبل متوجه فرمول محیط بیضی شدم البته باید بگم که فرمول مساحت رو دیده بودم اما طبق تحقیقات من هنوز فرمول دقیق بیضی به دست نیومده و این فرمولی رو که مینویسم فرمول تقریبی و نزدیک به هدفمون هست که توی کتابای درسی و رسم فنی مرجع آموزش هست. فرمول مساحت و محیط بیضی رو مینویسم که همه بتونن استفاده کنن : استفاده باذكر منبع بلامانع است.مرسی از آقا محمد که دو تا آدرس رو واسه ما جهت اطلاعات بیشتر گذاشتن که واستون میذارمشون :http://www.ebyte.it/library/docs/math07/EllipsePerimeterApprox07.htmlhttp://en.wikipedia.org/wiki/Ellipse
