محيط بيضي
روش رسم بیضی با دایره(سوم راهنمایی)
براي رسم بيضي با قطرهاي مشخص، ابتدا دو دايره متحدالمركز، يكي به اندازه قطر بزرگ بيضي و ديگري به اندازه كوچك بيضي رسم مي كنيم. يكي از دو دايره را به قسمتهاي مساوي تقسيم كرده از مركز به نقاط تقسيم روي محيط دايره وصل مي كنيم. ادامه دهيد تا محيط هر دو دايره را قطع كنند. حال از نقاط روي محيط دايره بزرگتر، خط عمود از نقاط روي دايره كوچتر خط افقي رسم مي كنيم تا خطوط يكديگر را قطع كنند. نقاط حاصل، محيط بيضي را تشكيل خواهند داد كه با وصل آنها به هم، بيضي مورد نظر رسم مي شود.
مساحت ومحيط اشكال هندسي
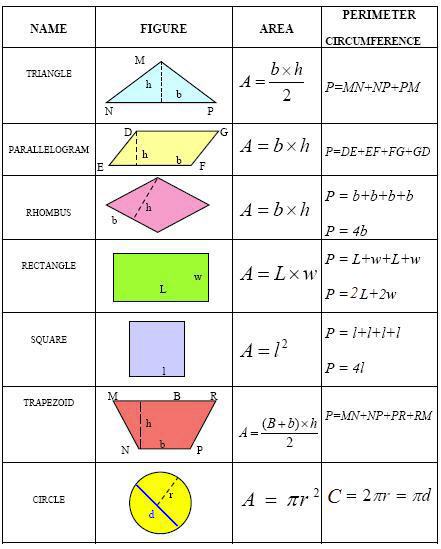
محیط و مساحت فرمول های ریاضی(محیط،مساحت و حجم اشکال هندسی) یک ضلع × خودش = مساحت مربع یک ضلع × 4 = محیط مربع طول × عرض = مساحت مستطیل 2× (طول + عرض) = محیط مستطیل 2 ÷ (قاعده × ارتفاع) = مساحت مثلث مجموع سه ضلع = محیط مثلث نصف ارتفاع × (قاعده بزرگ + قاعده کوچک) = مساحت ذوزنقه مجموع 4 ضلع = محیط ذوزنقه 2÷ (قطر بزرگ × قطر کوچک) = مساحت لوزی یک ضلع × 4 = محیط لوزی ارتفاع × قاعده = مساحت متوازی الاضلاع مجموع دو ضلع متوالی × 2 = محیط متوازی الاضلاع عدد پی × مجذور شعاع = مساحت دایره 14/3 × شعاع × شعاع 14/3 × قطر = محیط دایره مساحت کره چهار ×عدد پی × مجذور شعاع = مساحت کره حجم کره عدد پی × شعاع به توان 3 ضرب در عدد چهار سوم = حجم کره 14/3 × (نصف قطر کوچک × نصف قطر بزرگ) = مساحت بیضی یک ضلع × تعداد اضلاع = محیط چند ضلعی منتظم طول یال × مساحت یک وجه = حجم مکعب ارتفاع × عرض × طول = حجم مکعب مستطیل ارتفاع × قاعده = حجم مکعب ارتفاع هرم × مساحت قاعده هرم بر روي سه= حجم هرم ارتفاع × مساحت قاعده = حجم استوانه ارتفاع × محیط قاعده = مساحت جانبی سطح دو قاعده + مساحت جانبی = سطح کل استوانه مجموع مساحت سطوح جانبی = مساحت جانبی منشور مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی = مساحت کلی منشور ارتفاع × مساحت قاعده برروي سه= حجم مخروط محیط - مساحت - محیط و مساحت اشکال هندسی مساحت مـــربع = اندازه يـــک ضلع × ضلع دیگر محيــط مـــربــــع = يک ضلع × 42) مساحت مسـتطيـــــــل = طـول × عـرض محيط مستطيل = ( طول + عرض) × 23) مساحت مثلث = ( قاعده × ارتــــــفاع ) ÷ 2 محيط مثلث = مجموع سه ضلع4) مساحت مثلث متساوي الاضلاع = ( قاعده × ارتفاع ) ÷ 2 محيط مثلث متساوي الاضلاع = يک ضلع × 3 5) مساحت مثلث متساوي الساقين = ( قاعده × ارتفاع ) ÷ 2 محيط مثلث متساوي الساقين= مجموع سه ضلع 6) مساحت مثلث قائم الزاويه = ( قاعده × ارتفاع ) ÷ 2 محيط مثلث قائم الزاويه = مجموع سه ضلع 7) مساحت ذوزنقه = ( قاعده بزرگ + قاعده کوچک ) × نصف ارتفاع محيط ذوزنقه = مجموع چهار ضلع 8) مساحت لوزي = ( قطر بزرگ × قطر کوچک ) ÷ 2 محيط لوزي = يک ضلع × 4 9) مساحت متوازي الاضلاع = قاعده × ارتفاع محيط متوازي الاضلاع = مجموع دو ضلع متوالي × 2 10) مساحت دايره = عدد پي ( 14/3 ) × شعاع × شعاع محيط دايره = عدد پي ( 14/3 ) × قطر 11) مساحت کره = 4 × 14/3 × شعاع به توان دو حجم کره = چهار سوم × 14/3 × شعاع به توان سه 12) مساحت بيضي = (نصف قطر بزرگ × نصف قطر کوچک ) × 14/3 13 ) محيط چند ضلعي منتظم = يک ضلع × تعداد اضلاعش 14 ) حجم مکعب مستطيل = طـول × عـرض × ارتفاع حجم مکعب مربع = قاعده × ارتفاع ( طول يال×مساحت يک وجه) 15 ) حجم هرم = مساحت قاعده ي هرم × ارتفاع ...
روش بدست آوردن تقريبي محيط يك بيضي با خروج از مركز كم(سخت!)

سلام بر دوستان هميشه پيگير علم (نخ سوزن نجوم!)يك روش جديد بدست آوردم براي بدست آوردن تقريبي محيط بيضي براي خروج از مركز هاي كم :ادامه راه حل را مي توانيد از لينك زير دانلود كنيد :http://www.astroupload.com/uploads/13255026263.pngپس از خواندن راه حل :براي چك كردن جواب انتگرال نهايي مي توان e را صفر گفت و مي بينيم كه محيط 2.پيa مي شود كه برابر دايره اي به شعاع a است و در واقع هر بيضي كه e اش صفر باشد تبديل به دايره اي با شعاع نيم محور بزرگ بيضي مي شود.
توانايي تشخيص و ترسيم گونه هاي سطح
توانايي تشخيص و ترسيم گونه هاي سطح مقدمه: براي سطح نيز مانند،ديگر عناصر هنرهاي تجسمي تعاريف گوناگوني شده است. در ساده ترين تعريف، سطح به شكل بسته اي است كه داراي دو بُعد طول و عرض مي باشد. اشاره نموديم كه هر وقت نقطه از يك جهت رشد نموده و حركت كند، خط ايجاد مي شود. حال اگر همان نقطه از تمام جهات رشد نمايد، سطح ايجاد مي كند.در تعريف ديگر مي توانيم بگوييم كه سه نقطه در سه فاصله مرتبط با هم مطرح شوند، فضايي را مشخص مي كنند كه بصورت سطح نامرئي قابل درك مي باشد. بنابراين براي ايجاد سطح، وجود حداقل سه نقطه الزاميست. وجود سه نقطه در فضا و ارتباط آنها با يكديگر اولين و ساده ترين سطح دو بعدي يعني مثلث را به و جود مي آورد. با كمك مثلث مي توان به ديگر سطوح هندسي مانند مربع، مستطيل، ذوزنقه، متوازي الاضلاع، لوزي و.... دست يافت. سطوح نيز مانند خط و نقطه از حالتهاي گوناگون بوجود مي آيند. به عنوان مثال هرگاه دو خط موازي در فاصله اي نسبت به هم قرار گيرند، فضاي شكل گرفته بين آنها معرف يك سطح است. شناسايي سطحهاي ايزومتريك (هندسي) سطوح را مي توان به طور كلي به دو دسته تقسيم كرد: 1. سطوح هندسي 2. سطوح غيرهندسي سطوح هندسي عبارتند از مثلث، مربع، دايره، مستطيل،ذوزنقه، متوازي الاضلاع، بيضي و ساير اشكال هندسي. سطوح غير هندسي نيز شال كليه سطوح هستند كه شكل منظمي نداشته و معمولاً از قاعده خاصي پيروي نمي كنند. مانند كليه اشكال موجود در طبيعت. شناسايي سطوح اصلي هندسي (مثلث، مربع، دايره) سطوح هندسي داراي سه سطح اصلي مربع، مثلث و دايره مي باشند. تمامي سطح هاي هندسي از اين سه شكل با ترتيبي از آنها به وجود مي آيند. دايره: دايره شكل كاملي است. نماد حركت جاودانه و چرخش مداوم و مستمر در طبيعت مي باشد و بيانگر آمد و شد شب و روز، هفته ها، ماهها، فصلها و سالها است. دايره نماد نرمي، لطافت، سيال بودن، رونگرايي، آرامش،معنويت و آن جهاني بودن مي باشد. در هنر ايراني به نمونه هاي زيادي برخورد مي كنيم كه هنرمند از كادر يا تركيب بنديهاي دايره استفاده كرده است. دايره در تمام حالات داراي تعادل مي باشد. مربع: يكي از شكلهاي پايه در هندسه است كه متشكل از چهار زاويه و چهار ضلع مساوي و موازي است. مربع نماد صلابت، استواري و سكلون است و ميل به عدم تغيير وضعيت در او وجود دارد. مربع مظهر قدرت زمين و از زيباترين اشكال هندسي است. مثلث: (متوازي الاضلاع) هنگامي كه اين شكل بر قاعده خود قرار مي گيرد، از پايدارترين اشكال هندسي است و مثل يك كوه استوار به نظر مي رسد. اما در مقابل چنانچه بر رأس خود قرار گيرد حالتي كاملاً ناپايدار و متزلزل ...
فرمول مساحت اشکال هندسي
فرمول محیط ومساحت اشکال هندسی ویژه ی ابتدائیمساحت مـــربع = یـــک ضلع × خـــودش محیــط مـــربــــع = یک ضلع × 4 مساحت مسـتطیـــــــل = طـول × عـرض محیط مستطیل = ( طول + عرض) × 2 مساحت دایره = ( 14/3) × شعاع × شعاع محیط دایره = 14/ 3× قطر مساحت متوازی الاضلاع = قاعده × ارتفاع محیط متوازی الاضلاع = مجموع دو ضلع متوالی 2× مساحت ذوزنقه = نصف( قاعده بزرگ + قاعده کوچک×(ارتفاع محیط ذوزنقه = مجموع چهار ضلع مساحتمثلث = ( قاعده × ارتــــــفاع ) ÷ 2محیط مثلث = مجموع سهضلعمحیط مثلث متساوی الاضلاع = یک ضلع 3× مساحت لوزی = ( قطر بزرگ × قطر کوچک ) ÷ 2 محیط لوزی = یک ضلع × 4 مساحت بیضی = (نصف قطر بزرگ × نصف قطر کوچک ) × 14/3 محيط بيضي=14/3 × 2÷مجموع دو قطرمساحت چند ضلعی منتظم= محیط ضربدر نصف سهم(سهم= فاصله مرکز دایره محاطی تا هرضلع) محیط چند ضلعی منتظم = یک ضلع × تعداد اضلاعشمساحت جانبي مکعب مستطیل= محيط قاعده ×ارتفاعمساحت كل مکعب مستطیل=مساحت دو قاعده+مساحت جانبيحجم مکعب مستطیل = طـول × عـرض × ارتفاع مساحت جانبي مکعب مربع= يك بعد بتوان 2×4 يا مساحت يك وجه ×4مساحت كل مکعب مربع=يك بعد به توان 2×6 يا مساحت يك وجه ×6حجم مکعب مربع = مساحت قاعده × ارتفاع يا يك بعد بتوان 3مساحت جانبي هرم =محيط قاعده× سهم هرم ÷2 (طول شیب=سهم)مساحت كل هرم =مساحت قاعده+ سطح جانبيحجم هرم = مساحت قاعده ی هرم × ارتفاع هرم× یک سوممساحت جانبي مخروط =محيط قاعده× سهم هرم ÷2مساحت كل مخروط =مساحت قاعده+ سطح جانبيحجم مخروط = مساحت قاعده × یک سوم × ارتفاع مساحت جانبی استوانه = محیط قاعده × ارتفاع مساحت کل استوانه = سطح دو قاعده + مساحت جانبیحجم استوانه = مساحت قاعده × ارتفاع مساحت جانبی منشور = مجموع مساحت سطوح جانبی مساحت کل منشور = مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبیمساحت کره = 4 × 14/3 × شعاع ×شعاع حجم کره = چهار سوم ×14/3 × شعاع به توان سه
توانايي تشخيص و ترسيم گونه هاي سطح
مقدمه: براي سطح نيز مانند،ديگر عناصر هنرهاي تجسمي تعاريف گوناگوني شده است. در ساده ترين تعريف، سطح به شكل بسته اي است كه داراي دو بُعد طول و عرض مي باشد. اشاره نموديم كه هر وقت نقطه از يك جهت رشد نموده و حركت كند، خط ايجاد مي شود. حال اگر همان نقطه از تمام جهات رشد نمايد، سطح ايجاد مي كند.در تعريف ديگر مي توانيم بگوييم كه سه نقطه در سه فاصله مرتبط با هم مطرح شوند، فضايي را مشخص مي كنند كه بصورت سطح نامرئي قابل درك مي باشد. بنابراين براي ايجاد سطح، وجود حداقل سه نقطه الزاميست. وجود سه نقطه در فضا و ارتباط آنها با يكديگر اولين و ساده ترين سطح دو بعدي يعني مثلث را به و جود مي آورد. با كمك مثلث مي توان به ديگر سطوح هندسي مانند مربع، مستطيل، ذوزنقه، متوازي الاضلاع، لوزي و.... دست يافت. سطوح نيز مانند خط و نقطه از حالتهاي گوناگون بوجود مي آيند. به عنوان مثال هرگاه دو خط موازي در فاصله اي نسبت به هم قرار گيرند، فضاي شكل گرفته بين آنها معرف يك سطح است. شناسايي سطحهاي ايزومتريك (هندسي) سطوح را مي توان به طور كلي به دو دسته تقسيم كرد: 1. سطوح هندسي 2. سطوح غيرهندسي سطوح هندسي عبارتند از مثلث، مربع، دايره، مستطيل،ذوزنقه، متوازي الاضلاع، بيضي و ساير اشكال هندسي. سطوح غير هندسي نيز شال كليه سطوح هستند كه شكل منظمي نداشته و معمولاً از قاعده خاصي پيروي نمي كنند. مانند كليه اشكال موجود در طبيعت. شناسايي سطوح اصلي هندسي (مثلث، مربع، دايره) سطوح هندسي داراي سه سطح اصلي مربع، مثلث و دايره مي باشند. تمامي سطح هاي هندسي از اين سه شكل با ترتيبي از آنها به وجود مي آيند. دايره: دايره شكل كاملي است. نماد حركت جاودانه و چرخش مداوم و مستمر در طبيعت مي باشد و بيانگر آمد و شد شب و روز، هفته ها، ماهها، فصلها و سالها است. دايره نماد نرمي، لطافت، سيال بودن، رونگرايي، آرامش،معنويت و آن جهاني بودن مي باشد. در هنر ايراني به نمونه هاي زيادي برخورد مي كنيم كه هنرمند از كادر يا تركيب بنديهاي دايره استفاده كرده است. دايره در تمام حالات داراي تعادل مي باشد. مربع: يكي از شكلهاي پايه در هندسه است كه متشكل از چهار زاويه و چهار ضلع مساوي و موازي است. مربع نماد صلابت، استواري و سكلون است و ميل به عدم تغيير وضعيت در او وجود دارد. مربع مظهر قدرت زمين و از زيباترين اشكال هندسي است. مثلث: (متوازي الاضلاع) هنگامي كه اين شكل بر قاعده خود قرار مي گيرد، از پايدارترين اشكال هندسي است و مثل يك كوه استوار به نظر مي رسد. اما در مقابل چنانچه بر رأس خود قرار گيرد حالتي كاملاً ناپايدار و متزلزل دارد. مثلث به خاطر زواياي تندي كه دارد، حالتي تهاجمي و جهت ...
نقطه، خط، سطح، حجم و بافت : در گرافیک، نقاشی و عکاسی

مطلب از سایت پیک وان گرفته شده pic1.ir نویسنده : خانم سمیه سادات غلامی توانايي تشخيص و ترسيم نقطه: آشنايي با عنصر نقطه و توانايي تشخيص و ترسيم نقطه عکاس: مجید روئین فرد آنچه كه از قبل در رابطه با تعريف نقطه مي شناسيم، تعريفي است كه در درس هندسه خوانده ايم. (نقطه در محل تقاطع دو خط به وجود مي آيد) نقطه در علوم مختلف تعاريفي گوناگون دارد و در ادبيات نقطه در پايان جمله مي آيد. عکاس: ثمین ترک نقطه در هنرهاي تجسمي تعريف خاص خود را دارد. در اين محدوده اثر هر چيزي روي صفحه را نقطه مي گويند. مثل اثر نوك مداد يا قطره جوهر روي كاغذ و بسياري از موارد ديگر. در حاليكه اين نقطه ها مي توانند شكلهاي گوناگون داشته باشند و صرفاً به شكلي كه ما معمولاً تصور مي كنيم (دايره) ظاهر نشوند. بنابراين نقطه تجسمي فاقد شكل خاص بوده و اندازه آن نيز نسبي مي باشد. شكل نقطه ها در هنر تجسمي به دو صورت تقسيم مي شوند: الف) شكل هندسي مثل مثلث، مربع، دايره، بيضي و..... ب) شكل غير هندسي مانند اثر كف پا در يك صفحه. با توجه به تعريفها و نمونه هايي كه از نقطه آورده شده است اشاره به اين مطلب بسيار اهميت دارد كه اندازه نقطه در طبيعت متناسب با محيط و فضايي كه در آن قرار گرفته است تعريف شود. اين مفهوم (تناسب) را در مراجعه مستقيم به طبيعت به خوبي درك مي كنيد بعنوان مثال يك پنجره روشن در شب از فاصله دور يك نقطه محسوب مي شود. عکاس: آرمان خوش چهره گرچه ابعاد واقعي پنجره بزرگ است اما از فاصله دور در فضايي بزرگ يك نقطه نوراني، به حساب مي آيد. حال اگر فاصله خود را از پنجره كم كنيم تا جائيكه در كنار آن قرار بگيريم آن نقطه نوراني ديگر به حساب نمي آيد و يك سطح بزرگ ديده مي شود. نظير اين قبيل مثالها را در طبيعت بسيار ديده ايم. عکاس: حمید موذنی يك تكه ابر در آسمان و يا تك درختي بر روي تپه از فاصله بسيار دور در فضاي بزرگي كه قرار دارند نقطه محسوب مي شوند. بنابراين در طبيعت يك نقطه ممكن است سر يك سوزن، يك سيب، ستاره اي در آسمان، قايقي در دريا، ردپايي بر روي برف و.... باشد. شناسايي موقعيت نقطه در صفحه نقطه در صفحه مي تواند در قسمتهاي مختلف قرار گيرد. قرارگيري نقطه در محدوده هاي گوناگون احساسات متفاوتي را القا مي كند. چرا كه هر نقطه اي داراي انرژي دروني مي باشد. اگر كه در پايين صفحه قرار گيرد احساس سنگيني بيشتري را نسبت به همان نقطه كه در بالاي صفحه قرار دارد به همراه مي آورد. در واقع نقطه اي كه در پايين كادر است القا كننده وزن و سنگيني و جاذبه بيشتر است و نقطه اي كه در بالاي صفحه قرار دارد احساس سبك بودن و پرواز را دارا مي باشد. ميل به سكون، آرامش و جايگيري و عدم تمايل به تغيير ...
قطبش بيضوي
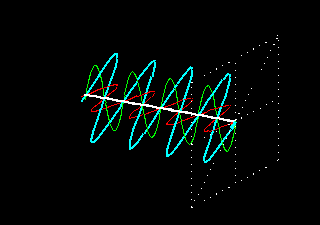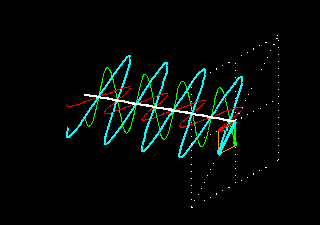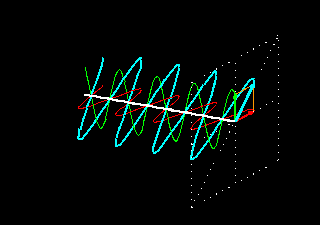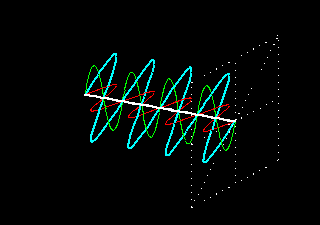
ديد كليحالتهاي مختلف قطبش ، مشخصه هر موج عرضي است. به عنوان مثال اگر ريسمان كشيده شدهاي را به بالا و پايين حركت دهيم يك موج قطبيده خطي توليد ميكنيم كه جابجايي آن روي صفحه قائم صورت ميگيرد. به همين ترتيب ميتوان موج قطبيده خطي ايجاد كرد كه جابجايي آن بر صفحه افقي واقع باشد. همچنين ميتوان انتهاي ريسمان را روي محيط يك دايره يا بيضي چرخاند تا موج قطبيده بيضيوار بدست آيد. در مورد چنين موجي ذرات ريسمان واقعا روي محيط يك دايره يا بيضي حركت ميكند. با انتشار دو موج قطبيده خطي در ريسمان هم ميتوان موج قطبيده بيضوي توليد كرد.برهمنهي دو موج قطبيده خطيدو موج الكترومغناطيسي را در نظر ميگيريم كه ميدان الكتريكي وابسته به آنها با روابط زير نشان داده ميشود:(E1 = xa1 Cos(kz - ωt + θ1(E2 = xa2 Cos(kz - ωt + θ2در روابط فوق a1 و a2 دامنه موجها ، x بردار يكاني واحد در جهت محور X و θ1 و θ2 ثابتهاي فاز به شمار ميروند. از آنجا كه دو ميدان فوق در راستاي محور X ارتعاش ميكنند، لذا موجهاي قطبيده خطي هستند كه در جهت محور z انتشار مييابند. چون ميدان الكتريكي كميتي برداري است، بنابراين ميدان الكتريكي برآيند بصورت جمع برداري دو ميدان الكتريكي فوق خواهد بود. ميدان الكتريكي موج برآيند بصورت زير خواهد بود:(E = E1 + E2 = xa Cos(Kz - ωt + θرابطه فوق نشان ميدهد كه موج برآيند هم يك موج قطبيده خطي است كه در همان راستاي انتشار دو موج اوليه انتشار مييابد. همچنين ارتعاش ميدان الكتريكي موج برآيند نيز در همان راستاي ارتعاش امواج اوليه است.شرايط ايجاد قطبش بيضويحال مانند مورد قبلي دو موج قطبيده خطي در نظر ميگيريم كه هر دو در يك جهت انتشار مييابند. اما جهت اتعاش ميدانهاي آنها بر هم عمود است. با اين فرض شرايط قطبش بيضوي بودن موج برآيند عبارتست از: تركيب اين دو موج كه داراي دامنه نامساوي هستند يك موج قطبيده بيضوي خواهد بود. اگر دامنه امواج اوليه برابر باشد، در اين صورت موج برآيند يك موج قطبيده بيضوي خواهد بود به شرط اينكه ثابت فاز موج برآيند مضرب صحيحي از π و يا π/2 نباشد. اگر ثابت فاز موج برآيند مضرب صحيحي از π باشد، در اينصورت موج برآيند قطبش خطي خواهد داشت كه معادل يك خط راست است. اگر ثابت فاز موج برايند مضرب صحيحي از π/2 بوده و دامنه امواج اوليه يكسان باشد، در اينصورت موج برايند قطبيده دايروي خواهد بود. بنابراين ميتوان گفت كه تركيب دو ارتعاش خطي عمود بر هم ، وقتي كه اختلاف فازي بين آنها برقرار باشد، يك ارتعاش بيضوي خواهد بود. يعني برآيند دو موج در هر لحظه يك ارتعاش خطي با دامنه معين است كه اين ارتعاش خطي يك چرخه كامل پيرامون بيضي را طي ...
محیط و مساحت
مساحت مـــربع = اندازه يـــک ضلع × ضلع دیگر محيــط مـــربــــع = يک ضلع × 42) مساحت مسـتطيـــــــل = طـول × عـرض محيط مستطيل = ( طول + عرض) × 23) مساحت مثلث = ( قاعده × ارتــــــفاع ) ÷ 2 محيط مثلث = مجموع سه ضلع4) مساحت مثلث متساوي الاضلاع = ( قاعده × ارتفاع ) ÷ 2 محيط مثلث متساوي الاضلاع = يک ضلع × 3 5) مساحت مثلث متساوي الساقين = ( قاعده × ارتفاع ) ÷ 2 محيط مثلث متساوي الساقين= مجموع سه ضلع 6) مساحت مثلث قائم الزاويه = ( قاعده × ارتفاع ) ÷ 2 محيط مثلث قائم الزاويه = مجموع سه ضلع 7) مساحت ذوزنقه = ( قاعده بزرگ + قاعده کوچک ) × نصف ارتفاع محيط ذوزنقه = مجموع چهار ضلع 8) مساحت لوزي = ( قطر بزرگ × قطر کوچک ) ÷ 2 محيط لوزي = يک ضلع × 4 9) مساحت متوازي الاضلاع = قاعده × ارتفاع محيط متوازي الاضلاع = مجموع دو ضلع متوالي × 2 10) مساحت دايره = عدد پي ( 14/3 ) × شعاع × شعاع محيط دايره = عدد پي ( 14/3 ) × قطر 11) مساحت کره = 4 × 14/3 × شعاع به توان دو حجم کره = چهار سوم × 14/3 × شعاع به توان سه 12) مساحت بيضي = (نصف قطر بزرگ × نصف قطر کوچک ) × 14/3 13 ) محيط چند ضلعي منتظم = يک ضلع × تعداد اضلاعش 14 ) حجم مکعب مستطيل = طـول × عـرض × ارتفاع حجم مکعب مربع = قاعده × ارتفاع ( طول يال×مساحت يک وجه) 15 ) حجم هرم = مساحت قاعده ي هرم × ارتفاع هرم× يک سوم 16) مساحت جانبي استوانه = محيط قاعده × ارتفاع حجم استوانه = مساحت قاعده × ارتفاعسطح کل استوانه = سطح دو قاعده + مساحت جانبي ( مساحت مجموع دو قاعده + ارتفاع × پيرامون قاعده ) 17) مساحت جانبي منشور = مجموع مساحت سطوح جانبي مساحت کلي منشور = مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبي 18) حجم مخروط = مساحت قاعده × يک سوم × ارتفاع
جزوه درسي گرافيك كاربردي ( قسمت دوم - سوم- چهارم و پنجم )
به نام خدا وسیع باش، و تنها، و سر به زیر، و سخت. «سهراب» جزوه درسي گرافيك كاربردي فصل دوم توانايي تشخيص و ترسيم علمي خط مقدمه براي خط تعاريف گوناگون و متفاوتي وجود دارد، از جمله اينكه خط در علم رياضي عبارت است از حركت و امتداد يك نقطه در سطح يا در فضا. همچنين خط از تكرار نقاط مختلف در كنار هم بوجود مي آيد. در تعريف ديگر خط از محل برخورد دو صفحه يا دو سطح با هم شكل مي گيرد. آشنايي با عناصر خط و انواع آن خط انواع گوناگون دارد. همچنانكه اشاره شد يك نوع خط همان تعريفي است كه در رياضيات تعريف مي شود و مورد ديگر خطي است كه در هنرهاي تجسمي مطرح مي گردد. خط اولي عنصر هنري است كه توسط انسان (در كودكي) بصورت ناخودآگاه و غيرعلمي، مورد استفاده قرار مي گيرد. در هنرهاي تجسمي خط دومين عنصر بصري است. عنصري است دو بعدي كه داراي ويژگيهاي طولي مي باشد. در واقع خط به منزله نقطه اي مي باشد كه وارد شدن عنصري است دو بعدي كه داراي ويژگي طولي بخشيده است و آنرا تبديل به يك عنصر بصري فعال و جهت دار نموده است. تكرار اين نقطه در يك جهت همراه با نيرو نيز، خط را شكل مي دهد. اين نقطه مي تواند داراي هر شكل بصري باشد. منظم، غير منظم، كلفت، نرم، خشن و.... خط نيز مانند نقطه داراي انرژي مي باشد. اما برخلاف نقطه كه داراي انرژي متمركز و تأكيد كننده در محل است. خط داراي انرژي فعال و پرتحركي است. صورت ديگر خط، خط در طبيعت است. خط در زندگي روزمره و اطراف ما حضور پر رنگ و قابل توجهي دارد. پيرامون ما مملو از جلوه هاي گوناگون خط است در اين زمينه مي توان به موارد بسيار اشاره كرد مانند مسير حركت يك رود، ريزش آبشار، رديف درختان پشت سرهم در يكطرف جاده، مسير مارپيچي جاده در كوه، سيمهاي برق و بسياري از موارد ديگر كه شما مي توانيد با نگاه دقيق در اطراف خود آنها را كشف كنيد. توجه داشته باشيد كه خطوط فرضي، داراي جهت، نيرو و انرژي مي باشند خطوط داراي قابليتهاي متفاوتي هستند اين قابليتها در خلق اثر هنري به هنرمند بسيار كمك مي كند به عنوان مثال از ويژگي ضخامت خطوط مي توانيم براي نمايش دوري و نزديكي در اثر هنري استفاده كنيم. شناسايي ويژگيهاي خط خط داراي ويژگيهايي است كه از جمله مهمترين آنها حركت، پويايي و جهت مي باشد. با اين وجود همچنانكه نقطه در طبيعت با اشكال متنوع ظاهر مي گردد، خط نيز در طبيعت به شكلهاي مختلف وجود دارد. هر كدام از اين اشكال داراي ويژگيهاي گوناگون و القا كننده حالات مختلفي مي باشند كه در زير به مواردي از آنها اشاره مي كنيم: خط راست افقي: حس آرامش و سكون را تداعي مي كند. ...
