محاسبه مساحت اشکال هندسی
روش محاسبه سطح مثلث و اشکال هندسی
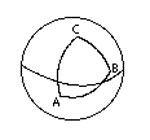
مثلث ار اساسی ترین اشکال در هندسه میباشد.یک مثلث دارای سه راس است که سه ضلع این رئوس را به هم وصل میکند.در هندسه اقلیدسی این اضلاع خطوطی مستقیم هستند. ولی در هندسه کروی این اضلاع کمان هایی از دایره عظیمه میباشند.این دو نوع مثلث را میتوانید در شکلهای روبرو مشاهده نمایید. انواع مثلثمثلث متساوی الاضلاع: مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای داخلی این مثلث نیز با هم برابرند.مثلث متساوی الساقین: مثلثی است که دارای دو ضلع با طولهای مساوی استو دو زاویه داخلی برابر دارد.البته مثلث میتواند دارای سه ضلع با طولهای مختلف و زوایای غیر مساوی باشد.مثلث قائم الزاویه: مثلثی را گویند که یکی از زوایای آن 90درجه باشد.نسبت های مثلثاتی مانند sin و cos ،بر روی مثلث قائم الزاویه تعریف میشوند.مثلث منفرجه: مثلثی را گویند که یکی از زوایای داخلی آن بیشتر از 90 درجه باشد.مثلث حاده : مثلثی را گویند که تمام زوایای داخلی آن کمتر از 90 درجه باشد.300 سال قبل از میلاد اقلیدس ،اصول اولیه درباره مثلث را ارائه داد.به عنوان مثال یکی از اصول مهم در مورد مثلث این است که مجموع زوایای داخلی یک مثلث برابر 180 درجه است. بر اساس این اصل میتوان با معلوم بودن دو زاویه از مثلث اندازه زاویه سوم را بدست آورد.یکی از مهمترین قضایای موجود در مثلثات قضیه فیثاغورث میباشد.در این قضیه رابطه بین وتر و اضلاع قائم یک مثلث قائم الزاویه بیان میشود. محاسبه مساحت مثلثبرای محاسبه مساحت یک مثلث روشهای مختلفی وجود داردو در ادامه به توضیح این روشها میپردازیم روش هندسیبرای محاسبه مساحت یک مثلث باید طول ارتفاع مثلث و نیز طول قاعده(ضلعی که ارتفاع بر آن عمود است) آن را داشته باشیم.آنگاه میتوانیم از فرمول زیر استفاده کنیم: در این فرمول b طول قاعده و h طول ارتفاع مثلث میباشد. در شکل زیر نحوه بدست آمدن این فرمول بیان شده است: تبدیل مثلث به یک متوازی الاضلاع که دو برابر مثلث مساحت دارد وسپس تبدیل متوازی الضلاع به یک مستطیلبرای پیدا کردن مساحت مثلث (قسمت سبز) ابتدا یک کپی از مثلث (قسمت آبی) را برداشته و آن را 180 درجه میچرخانیم و به مثلث اولیه متصل میکنیم تا یک متوازی الاضلاع بدست آید. با بریدن قسمتی از متوازی الاضلاع و متصل کردن آن به ضلع دیگر آن(همانند شکل) یک مستطیل ایجاد میشود. چون مساحت مستطیل برابر bh است .پس مساحت مثلث اولیه، نصف این مساحت خواهد بود.روش برداری محاسبه مساحت متوازی الاضلاع با استفادهاز ضرب خارجی دو بردارمساحت یک متوازی الاضلاع را میتوان با استفاده از بردارها محاسبه کرد.اگر AB,AC را مطابق شکل فرض کنیم آنگاه مساحت ABCD برابر |AB × AC| خواهد بود.این ...
فرمول محاسبه اشکال هندسی
فرمول محاسبه مساحت ومحیط اشکال هندسی نام شکل محیط مساحت تعداد خط تقارن تعداد قطر مربع اندازه یک ضلع × 4 اندازه یک ضلع × خودش 4 2 مستطیل (طول + عرض) × 2 طول × عرض 2 2 متوازی الاضلاع (مجموع 2 ضلع متوالی) × 2 قاعده × ارتفاع ندارد 2 ذوزنقه متساوی الساقین مجموع 4 ضلع(اضلاع) مجموع دو قاعده×ارتفاع تقسیم بر2 1 2 ذوزنقه قائم الزاویه مجموع 4 ضلع(اضلاع) مجموع دو قاعده×ارتفاع تقسیم بر2 ندارد 2 لوزی اندازه یک ضلع × 4 حاصلضرب دو قطر تقسیم بر 2 2 2 مثلث قائم الزاویه مجموع سه ضلع قاعده ×ارتفاع تقسیم بر 2 ندارد ندارد مثلث متساوی الساقین مجموع سه ضلع قاعده ×ارتفاع تقسیم بر 2 1 ندارد مثلث متساوی الاضلاع مجموع سه ضلع قاعده ×ارتفاع تقسیم بر 2 3 ندارد مثلث مختلف الاضلاع مجموع سه ضلع قاعده ×ارتفاع تقسیم بر 2 ندارد ندارد دایره قطر ×14/3 شعاع × شعاع × 14/3 بی شمار بی شمار
محاسبه محیط + مساحت + حجم اشکال هندسی

نرم افزار ترسیم اشکال هندسی GeoGebra v4.0.27 نرم افزار Geogebra محصول تیم متخصص با پشتیبانی دانشگاه سالزبورگ اتریش و سرپرستی مارکوس هوهن وارتر است که برای ترسیم اشکال هندسی به کار میرود. نرم افزار پوشش نسبتاً جامعی به مباحث حساب، جبر و هندسه فراهم کرده است. در برنامه محیط ترسیم اشکال هندسی، محیط ورود فرمان های ریاضی و ناحیه اطلاعات جبری در نظر گرفته شده است. خروجی جاوا اپلت این نرم افزار بدون نقص به همراه گزینه های فراوانی است که طراح آموزشی را قادر به تولید طرح درس های تعاملی با کیفیت بالا می کند. نرم افزار GeoGebra در مقایسه با دیگر نرم افزارها از لحاظ توانمندی های ترسیمی، ظاهر، وسعت عمل، محتوای آموزشی برای معلمین و دانش آموزان، ارتباط با کاربران، خروجی جاوا و بروز بودن مناسب ترین نرم افزار محسوب می شود.مطلب و نرم افزار فوق از سایت پی سی دانلوداستخراج گردیده است
فرمول محاسبه حجم اشکال هندسی

فرمول های ریاضی(محیط،مساحت و حجم اشکال هندسی) یک ضلع × خودش = مساحت مربع یک ضلع × ۴ = محیط مربع طول × عرض = مساحت مستطیل ۲× (طول + عرض) = محیط مستطیل ۲ ÷ (قاعده × ارتفاع) = مساحت مثلث مجموع سه ضلع = محیط مثلث نصف ارتفاع × (قاعده بزرگ + قاعده کوچک) = مساحت ذوزنقه مجموع ۴ ضلع = محیط ذوزنقه ۲÷ (قطر بزرگ × قطر کوچک) = مساحت لوزی یک ضلع × ۴ = محیط لوزی ارتفاع × قاعده = مساحت متوازی الاضلاع مجموع دو ضلع متوالی × ۲ = محیط متوازی الاضلاع عدد پی × مجذور شعاع = مساحت دایره ۱۴/۳ × شعاع × شعاع ۱۴/۳ × قطر = محیط دایره مساحت کره چهار ×عدد پی × مجذور شعاع = مساحت کره حجم کره عدد پی × شعاع به توان ۳ = حجم کره ۱۴/۳ × (نصف قطر کوچک × نصف قطر بزرگ) = مساحت بیضی یک ضلع × تعداد اضلاع = محیط چند ضلعی منتظم طول یال × مساحت یک وجه = حجم مکعب ارتفاع × عرض × طول = حجم مکعب مستطیل ارتفاع × قاعده = حجم مکعب ارتفاع هرم × مساحت قاعده هرم = حجم هرم ارتفاع × مساحت قاعده = حجم استوانه ارتفاع × محیط قاعده = مساحت جانبی سطح دو قاعده + مساحت جانبی = سطح کل استوانه مجموع مساحت سطوح جانبی = مساحت جانبی منشور مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی = مساحت کلی منشور ارتفاع × مساحت قاعده = حجم مخروط
حجم ومساحت اشکال هندسی /ریاضی ششم
دانش آموزان عزیز :در ایام تعطیلات نوروز با مطالعه و تمرین بخش مساحت و حجم به اطلاعات خود در این زمینه بیفزایید حجم:(Volume) حجم در لغت به معنی برآمدگی و ستبری و جسامت چیزی می باشد و در اصطلاح هندسه گنجایش و ظرفیت جسم و آن مقداری از فضا که جسم آن را اشغال می کند, را نشان می دهد. منشور: (Prism) منشور در لغت به معنی پراکنده, نشر شده, زنده شده و مبعوث است و در اصطلاح هندسه نام شکلی است که دو قاعده دارد که دو چند ضلعی مساوی هستند و بدنه منشور(سطح جانبی منشور ) از مستطیلها یا متوازی الاضلاع ها تشکیل شده است. معرفی منشور 5 پهلو: í نام شکل: منشور 5 پهلو í یال های منشور: 'EE',DD',CC',BB',AA í وجه منشور: هر کدام از مستطیل های جانبی را یک وجه منشور می نامند. í ارتفاع منشور: از آنجا که هر کدام از یال ها بر دو قاعده منشور عمود می باشند, لذا ارتفاع منشور با اندازه هر یک از یال ها برابر است. í قاعده ی منشور: منشور دو قاعده دارد. ABCDE و 'A'B'C'D'E که دو پنج ضلعی مساوی اند. رابطه های مهم: ارتفاع × مساحت قاعده = حجم منشور ارتفاع × محیط قاعده = مساحت جانبی منشور مساحت دو قاعده + مساحت جانبی = مساحت کل منشور استوانه: (Cylinder) نام شکلی است که دو قاعده دارد که دو دایره مساوی هستند و بر جانبی راست استوار است. اگر مستطیل را حول طول آن دوران دهیم, شکل فضایی حاصل استوانه نامیده می شود. در این صورت طول مستطیل ارتفاع استوانه و عرض آن شعاع قاعده استوانه می باشد. در شکل بالا مستطیل ABCD را حول طول آن دوران داده ایم و استوانه بوجود آمده است. رابطه های مهم: ارتفاع×مساحت قاعده(دایره) = حجم استوانه ارتفاع×محیط قاعده(دایره) = مساحت جانبی استوانه مساحت دو قاعده + مساحت جانبی = مساحت کل استوانه هرم: (pyramid) هرم در لغت به معنی سخت پیر گردیدن و کلان سال شدن است و در اصطلاح هندسه حجمی است که قاعده آن یک چند ضلعی و وجوه جانبی اش مثلثهایی باشند که همه به یک رأس مشترک(رأس هرم) منتهی می شوند. معرفی هرم منتظم: í نام شکل: هرم منتظم. í رأس هرم: نقطه S í ارتفاع هرم: پاره خطی است که از رأس هرم به مرکز قاعده ی هرم عمود است(SO) í قاعده هرم: پنج ضلعی منتظم ABCDE í سهم هرم: ارتفاع مثلث های جانبی, ارتفاع هر وجه جانبی هرم منتظم(SH). í وجه هرم: هر یک از مثلث هایی که بدنه هرم را می پوشانند را یک وجه جانبی می نامیم. í یال هرم: محل تقاطع هر دو وجه جانبی را یال هرم می نامیم. SE,SD,SC,SB,SA رابطه های مهم: مخروط : (cone) مخروط به معنی خراشیده شده ، تراشیده شده و خراطی شده است ودر اصطلاح هندسه حجمی است که از دوران مثلث قائم الزاویه حول یک ضلع آن به دست می آید . کله قند و کلاه بوقی ...
مثلث و اشکال هندسی
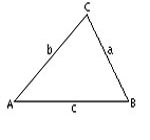
مثلث ار اساسی ترین اشکال در هندسه میباشد.یک مثلث دارای سه راس است که سه ضلع این رئوس را به هم وصل میکند.در هندسه اقلیدسی این اضلاع خطوطی مستقیم هستند. ولی در هندسه کروی این اضلاع کمان هایی از دایره عظیمه میباشند.این دو نوع مثلث را میتوانید در شکلهای روبرو مشاهده نمایید. انواع مثلثمثلث متساوی الاضلاع: مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای داخلی این مثلث نیز با هم برابرند. مثلث متساوی الساقین: مثلثی است که دارای دو ضلع با طولهای مساوی استو دو زاویه داخلی برابر دارد.البته مثلث میتواند دارای سه ضلع با طولهای مختلف و زوایای غیر مساوی باشد.مثلث قائم الزاویه: مثلثی را گویند که یکی از زوایای آن 90درجه باشد.نسبت های مثلثاتی مانند sin و cos ،بر روی مثلث قائم الزاویه تعریف میشوند. مثلث منفرجه: مثلثی را گویند که یکی از زوایای داخلی آن بیشتر از 90 درجه باشد. مثلث حاده : مثلثی را گویند که تمام زوایای داخلی آن کمتر از 90 درجه باشد. 300 سال قبل از میلاد اقلیدس ،اصول اولیه درباره مثلث را ارائه داد.به عنوان مثال یکی از اصول مهم در مورد مثلث این است که مجموع زوایای داخلی یک مثلث برابر 180 درجه است. بر اساس این اصل میتوان با معلوم بودن دو زاویه از مثلث اندازه زاویه سوم را بدست آورد.یکی از مهمترین قضایای موجود در مثلثات قضیه فیثاغورث میباشد.در این قضیه رابطه بین وتر و اضلاع قائم یک مثلث قائم الزاویه بیان میشود. محاسبه مساحت مثلثبرای محاسبه مساحت یک مثلث روشهای مختلفی وجود داردو در ادامه به توضیح این روشها میپردازیم روش هندسیبرای محاسبه مساحت یک مثلث باید طول ارتفاع مثلث و نیز طول قاعده(ضلعی که ارتفاع بر آن عمود است) آن را داشته باشیم.آنگاه میتوانیم از فرمول زیر استفاده کنیم: در این فرمول b طول قاعده و h طول ارتفاع مثلث میباشد. در شکل زیر نحوه بدست آمدن این فرمول بیان شده است: تبدیل مثلث به یک متوازی الاضلاع که دو برابر مثلث مساحت دارد وسپس تبدیل متوازی الضلاع به یک مستطیلبرای پیدا کردن مساحت مثلث (قسمت سبز) ابتدا یک کپی از مثلث (قسمت آبی) را برداشته و آن را 180 درجه میچرخانیم و به مثلث اولیه متصل میکنیم تا یک متوازی الاضلاع بدست آید. با بریدن قسمتی از متوازی الاضلاع و متصل کردن آن به ضلع دیگر آن(همانند شکل) یک مستطیل ایجاد میشود. چون مساحت مستطیل برابر bh است .پس مساحت مثلث اولیه، نصف این مساحت خواهد بود. روش برداری محاسبه مساحت متوازی الاضلاع با استفادهاز ضرب خارجی دو بردارمساحت یک متوازی الاضلاع را میتوان با استفاده از بردارها محاسبه کرد.اگر AB,AC را مطابق شکل فرض کنیم آنگاه مساحت ABCD برابر |AB × AC| خواهد بود.این مفدار ...
روابط محاسبه محیط و مساحت اشکال هندسی
دریافت روابط محاسبه محیط و مساحت اشکال هندسی موضوعات مرتبط: ریاضی (70) برچسبها: فرمول محاسبه محیط و مساحت اشکال هندسی, فصل هفتم, اندازه گیری سطح و حجم
نرم افزار محاسبه مساحت و حجم اشکال هندسی منظم----Geomterical Calculator
سلام دوستان .یک چند وقتی نتونستم بیام اخه یک کار برداشته بودم ار شیر مرغ تا جون ادمیزاد داخلش کارای مختلف داشت. می خواستند بند خاکی احداث کنند باید تمام کاراش را می کردم . از پیاده کردن شکل بند که به صورت شکسته بود و محور مرکزی تا رفرانس گذاری و بعد هم توپوگرافی و استخراج پروفیل طولی و عرضی و در اخر هم ترسیم و محاسبه حجم عملیات خاکی.خیلی دردسر داشت ولی خوشبختانه امروز تموم شد . براتون یک نرم افزار میزارم که مساحت و حجم را محاسبه می کند. ولی کاربردش برای اشکال با شکل منظم هستش. تقریبا تمامی اشکال را داره . یک خصوصیت دیگر خوبش این هست که شما میتونید جرم را به نرم افزار معرفی کنید و نرم افزار وزن کل را در ابعادی که انتخاب کردید به شما می دهد. بر روي لينك زير براي دانلود كليك كنيد. click here to download نرم افزار محاسبه مساحت و حجم----GEOMETRICAL CALCULATOR نکته : وقتی صفحه باز شد گزینه دانلود در وسط صفحه قرار دارد بر روی آن کلیک کنید تا قادر به دانلود آن شوید. Geometrical CALCULATORfree downloadsize : 953 KB برای دیدن مطالب قبل به ارشیو موضوعی مراجعه نمایید.
مساحت ها ، محیط ها و حجم اشکال هندسی
۱) مساحت مـــربع = یـــک ضلع × خـــودش محیــط مـــربــــع = یک ضلع × ۴۲) مساحت مسـتطیـــــــل = طـول × عـرض محیط مستطیل = ( طول + عرض) × ۲۳) مساحت مثلث = ( قاعده × ارتــــــفاع ) ÷ ۲ محیط مثلث = مجموع سه ضلع۴) مساحت مثلث متساوی الاضلاع = ( قاعده × ارتفاع ) ÷ ۲ محیط مثلث متساوی الاضلاع = یک ضلع × ۳۵) مساحت مثلث متساوی الساقین = ( قاعده × ارتفاع ) ÷ ۲ محیط مثلث متساوی الساقین= مجموع سه ضلع۶) مساحت مثلث قائم الزاویه = ( قاعده × ارتفاع ) ÷ ۲ محیط مثلث قائم الزاویه = مجموع سه ضلع۷) مساحت ذوزنقه = ( قاعده بزرگ + قاعده کوچک ) × نصف ارتفاع محیط ذوزنقه = مجموع چهار ضلع۸) مساحت لوزی = ( قطر بزرگ × قطر کوچک ) ÷ ۲ محیط لوزی = یک ضلع × ۴۹) مساحت متوازی الاضلاع = قاعده × ارتفاع محیط متوازی الاضلاع = مجموع دو ضلع متوالی × ۲۱۰) مساحت دایره = عدد پی (3/14 ) × شعاع × شعاع محیط دایره = عدد پی ( 3/14 ) × قطر۱۱) مساحت کره = ۴ ×3/14 × شعاع به توان دو حجم کره = چهار سوم × 3/14 × شعاع به توان سه۱۲) مساحت بیضی = (نصف قطر بزرگ × نصف قطر کوچک ) ×3/14 ۱۳ ) محیط چند ضلعی منتظم = یک ضلع × تعداد اضلاعش۱۴ ) حجم مکعب مستطیل = طـول × عـرض × ارتفاع حجم مکعب مربع = قاعده × ارتفاع ( طول یال×مساحت یک وجه)۱۵ ) حجم هرم = مساحت قاعده ی هرم × ارتفاع هرم× یک سوم 16) مساحت جانبی استوانه = محیط قاعده × ارتفاع حجم استوانه = مساحتقاعده × ارتفاعسطح کل استوانه = سطح دو قاعده + مساحت جانبی ( مساحت مجموع دو قاعده + ارتفاع × پیرامون قاعده )۱۷) مساحت جانبی منشور = مجموع مساحت سطوح جانبی مساحت کلی منشور = مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی۱۸) حجم مخروط = مساحت قاعده × یک سوم × ارتفاع
