محاسبه محیط بیضی
بیضی کیست ؟؟؟ چیست ؟؟؟ مساحتش چیست ؟؟؟
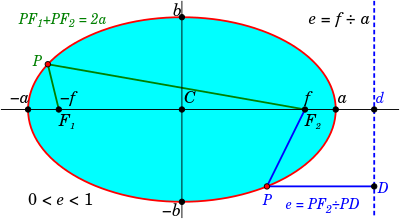
در هندسه، یک بیضی یک خم مسطح (خمی که در یک صفحهٔ اقلیدوسی تشکیل شدهاست.) است که از برخورد یک صفحه با یک مخروط ایجاد میشود به شرطی که خم ایجاد شده بسته باشد. برابر انگلیسی واژهٔ بیضی، ellipse از واژهٔ یونانی ἔλλειψις elleipsis به معنی falling short گرفته شدهاست. دایره حالت خاص بیضی است؛ که هنگامی بدست میآید که صفحهٔ عمود بر محور مخروط با آن برخورد کرده باشد. تعریف دیگر بیضی عبارت است از: مکان هندسی نقاطی از صفحهاست که مجموع فاصلههای آنها از دو نقطهٔ ثابت به یک اندازه ثابت مثبت باشد. بیضیها خمهای بسته و محدود از مقطع مخروط اند، این خمها از برخورد یک مخروط دایرهای با یک صفحه که از رأس مخروط نمیگذرد تشکیل شدهاند. دو نوع خم دیگر نیز از برخورد صفحه با مخروط میتوانند ایجاد شوند، این خمها همگی باز اند و تشکیل سهمی و هذلولی میدهند. در تعریفی دیگر بیضی مکان هندسی نقاطی است که نسبت فاصله آن از یک نقطه (کانون بیضی)، به فاصله آن از یک خط (خط هادی) برابر با عددی ثابت و کوچکتر از یک است. اجزای بیضی یک بیضی و برخی ویژگیهای ریاضی آن. یک بیضی یک خم بستهاست که نسبت به محورهای عمودی و افقی خود متقارن است. دو نقطه بر روی محیط بیضی که در دو سوی مخالف هم قرار دارند، یا به بیان دیگر، دو نقطه که خط واصل میان آنها از مرکز بیضی عبور میکند هنگامی در دورترین فاصله نسبت به هم قرار دارند که بر روی قطر بزرگ بیضی یا محور تقارن بزرگتر بیضی قرار گرفته باشند؛ و هنگامی کمترین مقدار را دارد که آن دو نقطه بر روی محور عمود بر قطر بزرگ، یعنی محور تقارن کوچکتر یا قطر کوچک بیضی قرار گرفته باشند.[۱] نیمقطر بزرگ (که در شکل با a نمایش داده شدهاست) و نیمقطر کوچک بیضی (که در شکل با b نمایش داده شدهاست) به ترتیب نیمی از قطر بزرگ و نیمی از قطر کوچک بیضی اند که گاهی به آنها شعاع کوچک (major radius) و شعاع بزرگ (minor radius) نیز میگویند. همچنین در انگلیسی به آنها major semi-axes و minor semi-axes نیز گفته میشود. محیط بیضی محیط بیضی به کمک انتگرالهای کامل بیضوی نوع دوم قابل محاسبهاست. البته فرمول صریحی همانند مساحت بیضی که برابر A = πab میباشد برای محیط بیضی وجود ندارد. و محیط بیضی تنها بوسیلهٔ سری نامتناهی قابل محاسبهاست: یا در روابط فوق ε خروج از مرکز بیضی است. در ضمن خروج از مرکزیت بیضی برابر با فاصلهٔ دو کانون تقسیم بر قطر اطول(2a) میباشد.حروف مرتبط : بیضی / اولین فرمول مساحت بیضی / مساحت بیضی / بیضی چیست / انتگرال بیضی / محیط بیضی /
سوال بپرسید وجوابتان را بگیرید
نام: ali تاريخ سوال: 10/05/1387سوال: why we are tierd at the end of the day? تاريخ پاسخ: 15/05/1387 پاسخ : سلام سوالتو باید از بخش زیست شناسی بپرسی. این لینک مرتبط : http://drzohrabi.ir/index.php?option=com_content&task=view&id=341&Itemid=117 (درستی اطلاعات لینکو تأیید نمی کنم!) نام: پریسا تاريخ سوال: 11/05/1387سوال: لطفا قضیه پروانه را توضیح دهید. تاريخ پاسخ: 15/05/1387 پاسخ : صرفا" به هر چی که خطاش با گذشت زمان زیاد بشه اثر پروانه ای گفته میشه. اگر در یک سیستم اختلالی کوچک ایجاد بشه و مشتق خطاش نسبت به زمان مثبت باشه با گذشت زمان زیاد دیگه نمیشه رفتار سیستم رو از همون اول پیش بینی کرد . برای مثال سیالات دارای چنین معادلات آشوب ناکی هستند و به همین دلیل کارشناسان آب و هوا نمیتوانند وضعیت هوا را تا زمان زیادی پیش بینی کنند. در زندگی اثر پروانه ای به صورت یک اتفاق کوچیکه که ممکنه مسیر زندگی فرد رو به کلی عوض کنه. صورت رسمی این نظریه میگه بال زدن پروانه ای در یک طرف کره ی زمین ممکن است باعث ایجاد گردبادی در طرف دیگر زمین شود. به هر حال اتفاقات کوچیک توی زندگیتون رو دست کم نگیرید http://apachiii.blogfa.com/ نام: amir تاريخ سوال: 24/04/1387سوال: باسلام فرمول حجم بیضی لطفا تاريخ پاسخ: 15/05/1387 پاسخ : سلام منظورتونو نمی فهمم بیضی یک شکل مسطحه و حجم ندارد اگر منظورتون مساحته : pi*a*b که a و b همان a و b ی معادله ی بیضی اند نام: حمید تاريخ سوال: 24/04/1387سوال: سلام سوال منو شما قبلا جواب دادین ولی من چیزی ازش نفهمیدم در یک صفحه شطرنج چند مربع وجود دارد لطفا توضیح دهید تاريخ پاسخ: 15/05/1387 پاسخ : سلام حمید جان در یک صفحه ی شطرنج چند تا مربع با ضلع 8 داریم؟! 1*1 چند تا با ضلع 7 داریم؟! 4 تا یعنی 2*2 . . . چند تا با ضلع 1 داریم؟! 64 تا یعنی 8 * 8 حالا همه اینا رو با هم جمع کن نام: سیروس تاريخ سوال: 17/04/1387سوال: مساحت هشت ضلعی تاريخ پاسخ: 15/05/1387 پاسخ : سلام هشت ضلعی را درون دایره فرض کن. و هشت ضلعی را یک مربع فرض کن به علاوه ی 4 مثلث رو اضلاع مربع. حالا به راحتی می تونی مساحت هشت ضلعی رو حساب کنی. نام: سبحان تاريخ سوال: 14/05/1387سوال: مساحت ومحیط مربع چگونه بدست میآید؟ تاريخ پاسخ: 15/05/1387 پاسخ : سلام اگر ضلع مربع را a فرض کنید : مساحت = a^2 محیط = 4*a نام: Madare Hadis تاريخ سوال: 03/02/1387سوال: سلام دختر من هنوز به مدرسه نمی روم اما خیلی از فرمولها را می داند. او از من فورمولهای زیر را میخواهد. می توانید آنها را بگویید: 1. مساحت مستطیل 2. محیط مستطیل 3. مساحت استوانه 4. محیط استوانه با تشکر تاريخ پاسخ: 08/02/1387 پاسخ : سلام آفرین بر ...
بیضی سنجی
1 - نفیسه شریفی (نویسنده اول) - دکتری تخصصی - مهندسی فناوری نانو - دانشگاه صنعتی شریف پژوهشکده علوم و فناوری نانو2 - فهیمه بهزادی (نویسنده مسئول) - دانشجوی دکتری تخصصی - فیزیک - دانشگاه شیراز دانشکده علوم پایه گروه فیزیکبیضی سنجی (Ellipsometry) روشی نوری است که برای مطالعه و بررسی لایه های نازک، ویژگی های نوری (ضریب شکست، ضریب جذب و توابع دی الکتریک) سطوح و فصل مشترک مواد استفاده می شود و می توان با استفاده از آن ضخامت، مورفولوژی، یکنواختی سطح، ریختشناسی (morphology)، کیفیت بلور، ترکیب شیمیایی و رسانایی مواد را ارزیابی کرد. در بیضی سنجی، معمولا شکست نور بررسی می شود و ویژگی هایی مانند ضخامت نمونه، ضریب شکست و ویژگی های دی الکتریک، موجب تغییرات در حالت نور قطبیده می شود. در بیضی سنجی تغییراتی که نور قطبیده پس از بازتاب یا عبور متحمل می شود مورد مطالعه قرار می گیرد که با بررسی تغییرات قطبش نور بازتاب شده از نمونه، میتوان در مورد لایههایی که ضخامت کم تر ازطول موج نور دارند، اطلاعاتی مانند ترکیب شیمیایی و رسانایی نیز به دست آورد.بیضیسنجی یک روش توانمند و غیرمخرب برای آنالیز لایههای بسیار نازک است. این روش قادر به اندازهگیری ضریب شکست، ضریب جذب و ضخامت لایههای نازک است. این وسیله بر این اساس کار می کند که بازتاب از فصل مشترک (سطح) دیالکتریک میتواند قطبش و فاز موج ورودی را تغییر دهد. این تغییرات به ضریب شکست ماده بستگی دارد. این روش میتواند خواص مختلفی از قبیل ضخامت، خواص نوری، مورفولوژی و حتی ترکیبات شیمیایی لایه را نیز مشخص کند. همچنین بیضیسنجی میتواند برای اندازهگیری ضخامت لایههایی با ضخامت نانومتری که روی زیرلایههای مختلف قرار دارند، استفاده شود. حتی به کمک این روش میتوان نمونه های چندلایه ای (Multilayer) را نیز بررسی و مطالعه نمود.بیضی سنجی در حوزههایی از قبیل زیست شناسی و پزشکی نیز روز به روز بیش تر مورد توجه قرار میگیرد. بیضیسنجی یک روش اپتیکی بسیار حساس است. این حساسیت به دلیل تغییر فاز نسبی نور قطبیدهای است که از یک لایه نازک منعکس میشود و یا از میان آن عبور میکند. اندازهگیری این تغییر فاز را میتوان در یک طول موج یا چندین طول موج و در یک زاویه برخورد یا در زوایای برخورد متفاوت انجام داد. اساس کار بیضی سنجیدر این روش نور منبع به عنوان موج الکترومغناطیسی و غیرقطبی، به وسیله قطبی کننده (polarizer) ، خطی و قطبیده می-شود. سپس توسط یک جبرانکننده (compensator)، قطبش خطی به قطبش دایرهای تبدیل میگردد. سپس نور حاصل به نمونه می رسد. بعد از برخورد نور قطبیده شده به نمونه و بازتاب از سطح ...
فرمول محاسبه حجم اشکال هندسی

فرمول های ریاضی(محیط،مساحت و حجم اشکال هندسی) یک ضلع × خودش = مساحت مربع یک ضلع × ۴ = محیط مربع طول × عرض = مساحت مستطیل ۲× (طول + عرض) = محیط مستطیل ۲ ÷ (قاعده × ارتفاع) = مساحت مثلث مجموع سه ضلع = محیط مثلث نصف ارتفاع × (قاعده بزرگ + قاعده کوچک) = مساحت ذوزنقه مجموع ۴ ضلع = محیط ذوزنقه ۲÷ (قطر بزرگ × قطر کوچک) = مساحت لوزی یک ضلع × ۴ = محیط لوزی ارتفاع × قاعده = مساحت متوازی الاضلاع مجموع دو ضلع متوالی × ۲ = محیط متوازی الاضلاع عدد پی × مجذور شعاع = مساحت دایره ۱۴/۳ × شعاع × شعاع ۱۴/۳ × قطر = محیط دایره مساحت کره چهار ×عدد پی × مجذور شعاع = مساحت کره حجم کره عدد پی × شعاع به توان ۳ = حجم کره ۱۴/۳ × (نصف قطر کوچک × نصف قطر بزرگ) = مساحت بیضی یک ضلع × تعداد اضلاع = محیط چند ضلعی منتظم طول یال × مساحت یک وجه = حجم مکعب ارتفاع × عرض × طول = حجم مکعب مستطیل ارتفاع × قاعده = حجم مکعب ارتفاع هرم × مساحت قاعده هرم = حجم هرم ارتفاع × مساحت قاعده = حجم استوانه ارتفاع × محیط قاعده = مساحت جانبی سطح دو قاعده + مساحت جانبی = سطح کل استوانه مجموع مساحت سطوح جانبی = مساحت جانبی منشور مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی = مساحت کلی منشور ارتفاع × مساحت قاعده = حجم مخروط
مقطع مخروطی
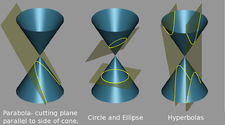
مقطع مخروطی از راست به چپ به ترتیب: هذلولی، بیضی و سهمی مقطع مخروطی، به خمی گویند که از برخورد یک مخروط و یک صفحه حاصل شود. معادله کلی معادله ی یک مقطع مخروطی به صورت معادله ی درجه دو زیر بر حسب بیان می شود:[۱] پانویس ↑ Sharma, p.150منبع Sharma, A.K. (2005). Text Book Of Conic Section. Discovery Publishing House. ISBN 8183560008, 9788183560009. + نوشته شده توسط احمد ذوالقدر دبیر ریاضی شهرستان زریندشت در پنجشنبه 1 فروردین1392 و ساعت 8:25 قبل از ظهر | نظر بدهید بیضی در هندسه، یک بیضی یک خم مسطح (خمی که در یک صفحهٔ اقلیدوسی تشکیل شدهاست.) است که از برخورد یک صفحه با یک مخروط ایجاد میشود به شرطی که خم ایجاد شده بسته باشد. برابر انگلیسی واژهٔ بیضی، ellipse از واژهٔ یونانی ἔλλειψις elleipsis به معنی falling short گرفته شدهاست. دایره حالت خاص بیضی است؛ که هنگامی بدست میآید که صفحهٔ عمود بر محور مخروط با آن برخورد کرده باشد. تعریف دیگر بیضی عبارت است از: مکان هندسی نقاطی از صفحهاست که مجموع فاصلههای آنها از دو نقطهٔ ثابت به یک اندازه ثابت مثبت باشد. بیضیها خمهای بسته و محدود از مقطع مخروط اند، این خمها از برخورد یک مخروط دایرهای با یک صفحه که از رأس مخروط نمیگذرد تشکیل شدهاند. دو نوع خم دیگر نیز از برخورد صفحه با مخروط میتوانند ایجاد شوند، این خمها همگی باز اند و تشکیل سهمی و هذلولی میدهند. در تعریفی دیگر بیضی مکان هندسی نقاطی است که نسبت فاصله آن از یک نقطه (کانون بیضی)، به فاصله آن از یک خط (خط هادی) برابر با عددی ثابت و کوچکتر از یک است.اجزای بیضی یک بیضی و برخی ویژگیهای ریاضی آن. یک بیضی یک خم بستهاست که نسبت به محورهای عمودی و افقی خود متقارن است. دو نقطه بر روی محیط بیضی که در دو سوی مخالف هم قرار دارند، یا به بیان دیگر، دو نقطه که خط واصل میان آنها از مرکز بیضی عبور میکند هنگامی در دورترین فاصله نسبت به هم قرار دارند که بر روی قطر بزرگ بیضی یا محور تقارن بزرگتر بیضی قرار گرفته باشند؛ و هنگامی کمترین مقدار را دارد که آن دو نقطه بر روی محور عمود بر قطر بزرگ، یعنی محور تقارن کوچکتر یا قطر کوچک بیضی قرار گرفته باشند.[۱] نیمقطر بزرگ (که در شکل با a نمایش داده شدهاست) و نیمقطر کوچک بیضی (که در شکل با b نمایش داده شدهاست) به ترتیب نیمی از قطر بزرگ و نیمی از قطر کوچک بیضی اند که گاهی به آنها شعاع کوچک (major radius) و شعاع بزرگ (minor radius) نیز میگویند. همچنین در انگلیسی به آنها major semi-axes و minor semi-axes نیز گفته میشود. محیط بیضی محیط بیضی به کمک انتگرالهای کامل بیضوی نوع دوم قابل محاسبهاست. البته فرمول صریحی همانند مساحت بیضی که برابر میباشد ...
