محاسبه رگرسیون
محاسبه رگرسیون خطی-آمار توصیفی بدون نیاز به نرم افزار
برای بدست آوردن ضرایب رگرسیون روی لینک رگرسیون خطی کلیک کنید. پنجره ای باز می شود که شامل دو ستون متغیر X و Y است. داده های مستقل را در ستون X و داده های وابسته را در ستون Y وارد کنید. با کلیک روی دکمه calc مقادیر عرض از مبدا (Intercept)٬ شیب (Slope) و ضریب همبستگی R برآورد شده را داریم. برای محاسبه آمار توصیفی داده ها روی لینک آمار توصیفی کلیک کنید. داده های خود را داخل مستطیل های سفید رنگ وارد کنید. با کلیک روی دکمه calc کمیت هایی چون تعداد (Observation)٬ مجموع مشاهدات (Sum)٬ میانگین (Mean) و... را خواهید داشت.
آموزش نحوه محاسبه مدل رگرسیون لجستیک Binomial logistic regression در نرمافزار SPSS
در بسیاری از پژوهش ها متغیر وابسته مورد مطالعه ماهیتا یک متغیر گسسته است که برای برآورد رخداد هر یک از سطوح نیازمند استفاده از رگرسیون های کیفی هستیم. رگرسیون های با متغیر وابسته گسسته دارای انواع مختلفی هستند که با توجه به ماهیت متغیر وابسته تعیین می شوند. اگر متغیر وابسته دو بعدی(dichotomous) باشد رگرسیون لجستیک Binomial (or binary) logistic regression برای بیان پیش بینی استفاده می شود. منظور از دو وجهی بودن، رخ داد یک واقعه تصادفی در دو موقعیت ممکنه است. به عنوان مثال خرید یا عدم خرید، ثبت نام یا عدم ثبت نام، ورشکسته شدن یا ورشکسته نشدن و ... متغیر هایی هستند که فقط دارای دو موقعیت هستند و مجموع احتمال هر یک آنها در نهایت یک خواهد شد. کاربرد این روش عمدتا در ابتدای ظهور در مورد کاربرد های پزشکی برای احتمال وقوع یک بیماری مورد استفاده قرار می گرفت. لیکن امروزه در تمام زمینه های علمی کاربرد وسیعی یافته است. به عنوان مثال مدیر سازمانی می خواهد بداند در مشارکت یا عدم مشارکت کارمندان کدام متغیر ها نقش پیش بینی دارند؟ مدیر تبلیغاتی می خواهد بداند در خرید یا عدم خرید یک محصول یا برند چه متغیر هایی مهم هستند؟ یک مرکز تحقیقات پزشکی می خواهد بداند در مبتلا شدن به بیماری عروق کرنری قلب چه متغیر هایی نقش پیش بینی کننده دارند؟ تا با اطلاع رسانی از احتمال وقوع کاسته شود. مشخصا در این موقعیت پژوهشی نمی توان از رگرسیون های معمولی برای پیش بینی رخداد این متغیر های وابسته استفاده نمود. در این نوع از رگرسیون از نسبت برتری odds که نسبت (p/(1-p) می باشد استفاده می شود و برای به دست آوردن مدل لوجیت از این رابطه باید از آن لگاریتم گرفت. لذا مدل عمومی رگرسیون لجستیک به شکل زیر خواهد بود. Ln (p/ (1-p) = intercept + b1*X1 + b2*X2 + ... + bk*Xk. از آنجائیکه رگرسیون لوجستیک از خاصیت حداکثر درستنمایی به جای حداقل مربعات مرسوم در رگرسیون خطی استفاده می کند، از روی این فرمول در نهایت می توان احتمالات پیش بینی شده را بر اساس قاعده زیر بیان نمود: p = e intercept + b1*X1 + b2*X2 + ... + Bk*Xk / (1+ e intercept + b1*X1 + b2*X2 + ... + Bk*Xk) معادله رگرسیون لجستیک در نرم افزار SPSS به شکل زیر برآورد می شود: z = ln(odds(event)) = ln(prob(event)/prob(nonevent))= ln(prob(event)/[1 - prob(event)]) = b0 + b1X1 + b2X2 + ..... + bkX پیش شرط های انجام رگرسیون خطی مانند وجود رابطه خطی بین متغیر های مستقل و وابسته، همسانی واریانس متغیر وابسته و متغیر های مستقل(Homoscedastic)، توزیع نرمال متغیر وابسته و باقیمانده ها یا خطای اندازه گیری مدل را نیاز ندارد. لیکن موضوع همراستایی چند گانه در رگرسیون لجستیک نیز وجود دارد که به معنای عملکرد خطی هر یک از متغیر های مستقل نسبت به یکدیگر است. برای این منظور ...
محاسبه رگرسیون توبیت (Tobit Regression) در Stata
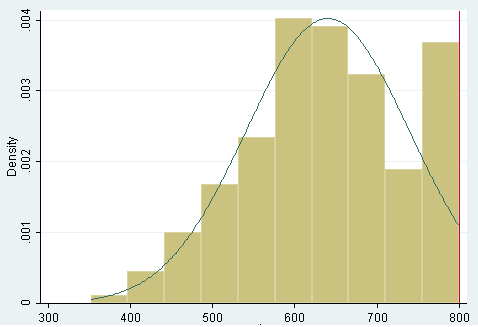
مدل های توبیت که گاها رگرسیون حساس شده و یا سانسور شده نامیده می شوند، به منظور بررسی روابط خطی در شرایطی که در مورد متغیر وابسته یک حد بحرانی در سمت راست یا چپ مشاهده شود استفاده می شود. از این رو به این نوع خاص از توابع پیش بینی رگرسیون سانسور شده نیز اطلاق می شود. وجود موارد فراتر از حد بحرانی یا پائین تر از حد بحرانی در متغیر وابسته بیانگر یک مشکل جدی و اریب در معادله رگرسیون است و نیازمند استفاده از رگرسیون توبیت است. به دیگر سخن وجود این سطح از پراکنش سبب خطای جدی در شرایط استفاده از رگرسیون خطی می شود. به عنوان مثال در نظر بگیرید محققی علاقه مند است متغیر های پیش بینی کننده سطح سرب آب آشامیدنی که وجود مقادیر بالای 15 ppb آن خطر ناک است را مطالعه کند به این منظور سن ساختمان مسکونی و وضعیت معیشتی را به عنوان متغیر های پیش بینی کننده مورد توجه قرار داد. یک مشکلی که در این رابطه وجود دارد این است که دستگاه تشخیص سرب مقادیر زیر 5 ppb را تشخیص نمی دهد و مقدار صفر را نشان می دهد در حالیکه این مقدار صفر واقعی نیست. لذا این برآورد در رگرسیون خطی اشتباه خواهد بود. به منظور مطالعه این روش در نرم افزار STATA یک مثال عملی مورد توجه قرار می گیرد. در نظر بگیرید در یک آزمون نظر سنجی یک برنامه تبلیغاتی کاربران به این برنامه از 0 تا 10 در قالب ایتم های مختلف نمره می دهند. حداقل نمره 200 و ماکزیمم آن 800 می باشد. افرادی که تمام آیتم ها را مثبت ارزیابی کرده باشند 800 را به برنامه داده اند و اگر تمام ایتم ها را منفی ارزیابی کنند 200 را به برنامه تبلیغاتی داده اند. لیکن افرادی که 800 می گیرند یا 200 الزاما همگی مانند هم نیستند. در این تحقیق 200 نفر مشارکت کردند که متغیر وابسته نمره ارزیابی یا ase و متغیر های مستقل شامل دو متغیر میزان تمایل به خرید و میزان تمایل به محصولات آن برند است. دستور زیر را به منظور کسب وضعیت توصیفی داده ها به کار می بریم. summarize ase purc bran Variable | Obs Mean Std. Dev. Min Max-------------+-------------------------------------------------------- ase | 200 640.035 99.21903 352 800 purc | 200 52.23 10.25294 28 76 bran | 200 52.645 9.368448 33 75 برای مشاهده فرم توزیع نیز از دستور زیر برای متغیر وابسته استفاده می کنیم. (histogram ase, normal bin(10) xline(800نتایج حاصله نشان می دهد که نمرات بین 750 تا 800 غالب داده های متغیر وابسته را نشان می دهند. با استفاده از دستور زیر این موضوع بهتر نمایان می شود. نتایج نشان می دهد که غالب این دیتا دارای یک اریب معنی دار است. histogram ase, discrete ...
محاسبه رگرسیون خطی
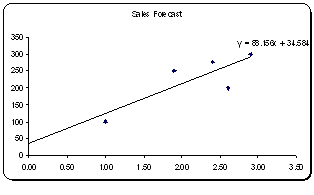
آموزش کامل محاسبه رگرسیون خطی همراه با مثال و نمودار برای دریافت فایل بر روی کلمه رگرسیون کلیک کنید.
کاربرد آنالیز رگرسیون خطی(Linear Regression) با استفاده از نرم افزار SAS
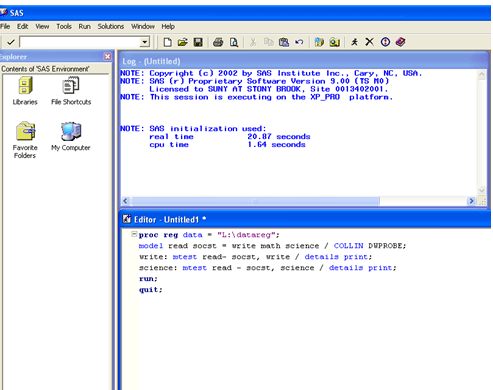
با توجه به سوالات مکرر دانشجویان در مورد نحوه محاسبه رگرسیون خطی در نرم افزار SASبر آن شدم تا محاسبه روش محاسبه این آزمون را به طور مختصر در این نوشتار ارائه دهم. اصولا کاربرد رگرسیون در مطالعات مختلف بسیار وسیع است و کمتر تحقیقی را می توان یافت که از رگرسیون ها برای پیش بینی ها استفاه نکرده باشد. خانواده رگرسیون ها بسیار گسترده بوده و دارای انواع مختلفی است که یکی از پر کاربرد ترین آنها، نوع خطی است. نرم افزا SAS به عنوان قویترین نرم افزار آمار مورد استفاده در بین محققان، کامل ترین روش محاسبه رگرسیون خطی را ارائه می دهد که محقق می تواند با توجه به نیاز خود از آن استفاده کند. نرم افزار SAS دارای محیط برنامه نویسی بسیار پیشرفته و کاملی است که تمام نیاز های آماری محققان را در سطوح مختلف برآورده می کند. در این نوشتار از ارائه فرمول ها پرهیز شده و سعی بر ارائه یک راهنمای کاربردی برای استفاده از این روش آماری در نرم افزار SASبود. انجام رگرسیون خطی چندگانه دارای پیش فرض هایی است که باید این قواعد را برای کسب نتیجه بهینه مورد توجه قرار داد. استقلال مشاهدات، ساختار کوواریانس عمومی در بین مشاهدات، همگونی واریانس های وضعیت خطاها بر متغیر های پیش بین و نرمال بودن توزیع چند متغیره باقیمانده ها. در مورد نرمال بودن توزیع چند متغیره، در نرم افزار هایی چون SPSS و SAS آزمون خاصی ارائه نمی شود و صرفا از طیق اسکتر پلات ها نحوه توزیع باقیمانده و نرمال بودن آن مورد قضاوت قرار می گیرد. در مورد همگونی واریانس های وضعیت خطاها بر متغیر های پیش بین، با توجه به اینکه اکثر ازمون های ارائه شده به نرمال بودن توزیع وابسته هستند؛ برای این منظور نرم افزار SAS از آماره F برای برازش کلی مدل رگرسیونی استفاده می کند. معنی داری آزمون F به معنای تحقق این پیش فرض رگرسیون خطی چند گانه است. برای آزمون هم خطی در رگرسیون از مقدار تولرانس یا تورش واریانس استفاده می شود که به این معنا است که اطلاعات هر متغیر پیش بین وارد شده به مدل تا چه حد توسط سایر متغیرهای مستقل قابل برآورد بوده است. برای این منظور بایدبه شاخص شرایط استناد نمود که باید مقدار آن زیر 15 برای مدل های خوب باشد و تا 30 قابل تحمل است لیکن مقادیر کمتر آن به معنای اعتبار بیشتر ضریب تعیین است. برای بررسی استقلال خطاها از یکدیگر نیز از آزمون دوربین واتسون استفاده می شود که باید بین 5/1 تا 5/2 باشد. در اینجا هدف بررسی حل یک مثال واقعی با نرم افزار SAS است. در نظر بگیرید محققی علاقه مند است تا بداند در دفعات مشاهده و یادآوری یک تیزر تلویزیونی، نقش متغیر هایی چون آشکار بودن پیام آن، منطقی بودن عناصر به ...
آموزش مقدماتی رگرسیون با نرم افزار اکسل

آموزش مقدماتی رگرسیون با نرم افزار اکسل نرم افزار اکسل (Excel) یکی از انواع صفحات گسترده ( spreadsheet) میباشد که برای اهداف گوناگون اطلاعاتی از جمله تحلیل آماری به کار میرود . صفحه های گسترده قابلیت تحلیل های بیشرفته آماری را ندارند ولی به دلیل سادگی و محیط زیبا برای کاربر ، محبوبیت دارند . بجز اکسل نرم افزارهای صفحه گسترده دیگری از جمله : Ability Spreadsheet - AppleWorks - Framework - Gnumeric - KDCalc - KSpread - Lotus 1-2-3 - Lotus Improv - Lotus Symphony - Origin - OpenOffice.org Calc - Quantrix Modeler - Quattro Pro - SpreadsheetGear for .NET - The Cruncher و VisiCalc ، برای سیستم های مختلف ساخته شده اند . برای تحلیل های پیشرفته آماری نرم افزار های زیادی وجود دارند که بعضی از آنها عبارتند از : R (زبان برنامه نویسی) SAS - S-Plus - SPSS و ... شروع از – صفر – : در ادامه بصورت مقدماتی انجام یک تحلیل رگرسیون خطی با استفاده از اکسل آموزش داده میشود . شما باید قبل از این آموزش با مفاهیم مقدماتی تحلیل رگرسیون از جمله : متغیر های پاسخ و مستقل ، ضریب تعیین ، ANOVA ، فاصله اطمینان ، نمودار نرمال و... آشنا باشید . در این آموزش از نسخه 2002 برنامه اکسل استفاده میکنیم ، که ظاهری شبیه به شکل زیر دارد : (با کلیک روی تصاویر موجود میتوانید آنها را بزرگتر ببینید ) داده ها را در ستون A و B به ترتیب برای متغیر وابسته (Y) و رگرسور (X) وارد میکنیم . برای مثال نمونه 20 تایی زیر وارد شده است برای انجام تحلیل های آماری نیاز به یک بسته اضافی (Add-in) داریم ، که بصورت زیر نصب میشود :از منوی Tools گزینه Add-Ins… را انتخاب کنید : در پنجره باز شده گزینه اول یعنی Analysis ToolPack را علامت بزنید و OK را انتخاب کنید . اگر گزینه اول از پیش دارای علامت تیک هست بدون انجام کاری OK را انتخاب کنید . در این مرحله ممکن است پیام زیر ظاهر شود که باید CD برنامه را در درایو قرار دهید و دکمه Yes را بزنید تا مراحل نصب تمام شود . بعد از این کار از منو Tools گزینه Data Analysis… را انتخاب کنید . از پنجره باز شده Regression را انتخاب کنید و کلید OK را بزنید . در این پنجره 4 قسمت وجود دارد : ورودی : روی فضای خالی روبروی عبارت Input Y Range : کلیک کنید و سلول های ستون A را از 1 تا 20 انتخاب نمایید یا مستقیماً عبارت زیرر را بنویسید : A$1:$A$20$ . (این کار محدوده متغیر وابسته را مشخص میکند . داده ها میتواند هر جای دیگر بصورت ستونی قرار گیرد و تنها عبارت بالا تغییر خواهد کرد . ) این کار را برای متغیر رگرسور نیز در فضای روبروی عبارت Input X Range تکرار کنید یا عبارت $B$1:$B$20 را تایپ کنید .اگر برای ستون داده ها در ردیف اول اسمی نوشته باشید باید گزینه Labels را علامت بزنید ، که در این مثال لازم نیست .گزینه مقابل هم برای رگرسیون ...
تحلیل رگرسیون و رگرسیون کاذب
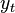
تحلیل رگرسیون تحلیل رگرسیونی یا تحلیل وایازشی فن و تکنیکی آماری برای بررسی و مدلسازی ارتباط بین متغیرها است. رگرسیون تقریباً در هر زمینهای از جمله مهندسی، فیزیک، اقتصاد، مدیریت، علوم زیستی، بیولوژی و علوم اجتماعی برای برآورد و پیشبینی مورد نیاز است. تحلیل رگرسیونی، یکی از پرکاربردترین روش در بین تکنیکهای آماری است. تعریف لغوی واژه رگرسیون(Regression) را از لحاظ لغوی در فرهنگ لغت به معنی پسروی، برگشت و بازگشت است. اما از دید آمار و ریاضیات به مفهوم بازگشت به یک مقدار متوسط یا میانگین بهکارمیرود. بدین معنی که برخی پدیدهها به مرور زمان از نظر کمی به طرف یک مقدار متوسط میل میکنند. تاریخچه در سال ۱۸۷۷ فرانسیس گالتون (به انگلیسی: Francis Galton) در مقالهای که درباره بازگشت به میانگین منتشر کردهبود. اظهار داشت که متوسط قد پسران دارای پدران قدبلند، کمتر از قد پدرانشان میباشد. به نحو مشابه متوسط قد پسران دارای پدران کوتاهقد نیز، بیشتر از قد پدرانشان گزارش شدهاست. به این ترتیب گالتون پدیده بازگشت به طرف میانگین را در دادههایش مورد تأکید قرارداد. برای گالتون رگرسیون مفهومی زیستشناختی داشت، اما کارهای او توسط کارل پیرسون (به انگلیسی: Karl Pearson) برای مفاهیم آماری توسعه دادهشد. گرچه گالتون برای تأکید بر پدیده «بازگشت به سمت مقدار متوسط» از تحلیل رگرسیون استفاده کرد، اما به هر حال امروزه واژه تحلیل رگرسیون جهت اشاره به مطالعات مربوط به روابط بین متغیرها به کار بردهمیشود. رگرسیون کاذب رگرسیون کاذب (به انگلیسی: regression) با فرض اینکه متغیرهای و مانا میباشند تخمینهای ما از پارامترها و تستهای و درست میباشد. برای نشاندادن سازگاری تخمینهای حداقل مربعات معمولی، ما از این نتایج زمانی که اندازه نمونه افزایش مییابد و واریانس نمونه به واریانس جامعه همگرا میشود، استفاده میکنیم. متأسفانه وقتی سری نامانا باشد واریانس خوش تعریف نیست، زیرا حول یک میانگین ثابت نوسان نمیکند. برای توضیح بیشتر دو متغیر و را در نظر بگیرید که بوسیله یک فرآیند گام تصادفی تعریف میشود. که و دارای توزیع مستقل میباشد.هیچ دلیلی برای ارتباط بین و وجود ندارد. یک محقق اگراثر را روی و یک جزء ثابت رگرس کند و رگرسیون زیر را انجام دهد : خط راست: نتایج این رگرسیون ممکن است بوسیله r^۲ بالا و خود همبستگی بالا بین باقیماندهها و همچنین دارای ارزش معنیداری برای پارامتر باشد. این پدیده به رگرسیون کاذب معروف است. در این گونه از موارد دو سری نامانا ارتباط کاذبی دارند به این علت که که هر دوی آنها در طول ...
آموزش رگرسیون چند متغیره در spss
کاربرد يک متغير براى پيشبينى متغير ديگر را رگرسيون مىگويند. رگرسيون با کاربرد يک متغير دانسته و مشخص، مقادير متغير غيرمشخص ديگرى را پيشبينى مىکند. رگرسيون بصورت دو متغيره و چند متغيره محاسبه مىشود. در رگرسيون دو متغيره، يک متغير مستقل و يک متغير تابع وجود دارد؛ ولى در رگرسيون چند متغيره يک متغير تابع و چند متغير مستقل وجود دارد؛ مثلاً در محاسبهٔ تأثير دو متغير تحصيلات و تجربه شغلى در درآمد، درآمد متغير تابع است و تحصيلات و تجربه شغلى دو متغير مستقل هستند. در ادامه یک فایل آموزش تصویری رگرسیون چند متغیره در نرم افزار spss قرار داده شده است. دانلود فایل
رگرسیون در علوم دامی
رگرسیون ارائه دهنده : محمد تیموریان رگرسیون ساده خطی توصیف کننده و بیانگر تغییرات یک متغیر وابسته بر پایه تغییرات یک متغیر مستقل می باشد در رگرسیون خطی چند گانه اثر دو یا چند متغیر مستقل بر متغیر وابسته مورد تجزیه و تحلیل قرار می گیرد. پارامترهای رگرسیون خطی به روش برآورد حداقل مربعات به گونه ای تعیین می گردد که خط رگرسیون، رابطه خطی موجود بین متغیر های وابسته و مستقل حاصل از نمونه را به بهترین وجه نمایان سازد می توان این پارامترها را از طریق روش ماتریسی و نرم افزار های مختلف محاسبه نمود تفاوت رگرسیون و همبستگی در رگرسیون هدف تعیین وابستگی متغیر وابستهy به متغیر مستقل x است ولی با استفاده از ضریب همبستگی می توان شدت و میزان رابطه خطی موجود در بین دو متغیر را مورد بررسی قرار داد رگرسیون رابطه بین یک متغیر تصادفی و یک یا چند متغیر ثابت را بیان می کندولی همبستگی، رابطه بین دو متغیر تصادفی را تعیین می کند ومقدار همبستگی بین 1-و1+ می باشد و بدون واحد است کاربرد رگرسیون رگرسیون به پیش گویی ارزش یک صفت بر اساس اطلاعات صفات دیگر کمک می کند با استفاده از رگرسیون ارزش اصلاحی یک صفت بر ارزش فنوتیپی همان صفت،می توان ارزش اصلاحی حیوان را بر اساس عملکرد خود فرد پیشگویی کرد از آنجا که به غیر از ارزش فنوتیپی بقیه ارزشها مثل ارزش اصلاحی ،تفاوت نتاج و قابلیت تولید به طور مستقیم قابل اندازه گیری نیست باید از ارزشهای پیش گویی شده استفاده کنیم که با معادلات پیش گویی می توانیم آنها را پیش گویی کنیم که به صورت زیر است: ارزش پیش گویی شده(برآوردارزش اصلاحی ،تفاوت نتاج مورد انتظاروحداکثر قابلیت تولید)=ضریب رگرسیون ضرب در معیارفنوتیپی(رکورد عملکرد فنوتیپی،متوسط عملکرد رکورد های فرد،برادر و خواهران ناتنی وی و غیره) وراثت پذیری توان دوم همبستگی بین ارزشهای فنوتیپی و ارزشهای اصلاحی و رگرسیون ارزش اصلاحی در ارزش فنوتیپی است تکرار پذیری همبستگی بین ارزش فنوتیپی و قابلیت تولید برای یک صفت در یک جامعه است و رگرسیون قابلیت تولید در ارزش فنوتیپی است آزمون رگرسیون برای ازمون اینکه آیا رابطه خطی بدست آمده معنی دار است از آزمونهای tو Fاستفاده می شود tوFهر دو برای آزمون فرض 0=1b:0Hاستفاده می شوند 2t=F تغییرات موجود در مدل رگرسیون تغییرات کل متغیر وابسته =مجموع مربعات کل=پراکنش پیرامون میانگینy تغییرات محاسبه شده توسط مدل= مجموع مربعات رگرسیون تغییرات محاسبه نشده توسط مدل=همان پراکنش اطراف yتخمینی است=مجموع مربعات مانده ها اگر فرض معنی دار نشود به این معنی است که رگرسیون خطی بین دو متغیر وجود ندارد ولی ممکن است ...
