قواعد لگاریتم
لگاریتم و قواعد آن
کلیک کنید
لگاریتم
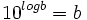
مقدمه در جبر عموما لگاریتم معمولی یا لگاریتم در پایه 10 عدد b را توانی تعریف میکنند که 10 باید به آن برسد تا b بدست آید: . فرض کنیم چنین عددی موجود بوده و از لگاریتمها برای سادهکردن ضرب اعدادی که ارقام اعشاری زیادی دارند استفاده میکنیم. تعریف تابع لگاریتم طبیعی بصورت زیر نمایش داده میشود: به ازای هر x بزرگتر از 1 ، این انتگرال مساحت ناحیهای را نشان میدهد که از بالا به خم از پایین به محور t از طرف چپ به خط t=1 ، و از طرف راست به خط t=x محدود است. تاریخچه در اواخر قرن شانزدهم یک بارون اسکاتلندی به نام جان نپر (1550-1617) ابزاری بنام لگاریتم ابداع کرد که با تبدیل ضرب به جمع کار محاسبه را ساده میکند؛ یعنی داریم: لگاریتم x + لگاریتم a = لگاریتم ax برای ضرب دو عدد مثبت x,a از یک جدول ، لگاریتمهای x,a را پیدا میکنیم، سپس این لگاریتمها را بهم میافزائیم مجموع حاصل را در داخل جدول مییابیم، و بالاخره حاصلضرب مطلوب ax را از حاشیه جدول میخوانیم. مسلما در دست داشتن جدول کلید کار بود، به همین سبب نپر در دو دهه آخر زندگیاش را صرف تهیه جدولی کرد که هیچگاه نتوانست آن را تمام کند. و این در حالی بود که تیکو براهه ستاره شناس ، مشتاقانه در انتظار این جدول بود تا میتواند محاسبات خودش را تسریع بخشد مشتق تابع لگاریتم طبیعی چون تابع با انتگرال ذکر شده در قسمت تعریف ، تعریف میشود، فورا از نخستین قضیه اساسی حساب دیفرانسیل و انتگرال نتیجه میشود که مشتق تابع برابر خواهد بود. بنابراین اگر u تابع مشتقپذیری از x باشد، آنگاه از قاعده زنجیری داریم: فرمول کلیتر زیر بدست میآید: مشتقگیری لگاریتمی گاهی یک تابع با معادلهای پیچیده داده شده با گرفتن لگاریتم از طرفین آن پیش از مشتقگیری میتوان مشتقش را سریعتر حساب کرد. خواص قلمرو: مجموعه تمام اعداد حقیقی مثبت ، x>0 برد: مجموعه تمام اعداد حقیقی این تابع بر قلمرو خود پیوسته و صعودی است هر گاه آنگاه . این تابع یک تابع یکبهیک از قلمرو خود به بردش است، بنابراین دارای معکوس است. حاصلضرب ، خارج قسمت و توان: هر گاه x,a دو عدد مثبت باشند. آنگاه:معکوس تابع لگاریتم چون یکبهیک و مشتقپذیر است، دارای معکوس مشتقپذیر میباشد نمودار منعکس نمودار تابع نسبت به خط y=x است. این نمودار تابع نیز میباشد. تابع به ازای هر عدد حقیقی x مساوی میباشد. تابع حاصل تابع مشتق پذیری از x است که به ازای هر x حقیقی تعریف شده است و بعنوان تابع نمایی از آن یاد میشود که e را پایه و x نما خوانده میشود. همچنین توجه میکنیم که حد تابع نمایی زمانی که x بسمت بینهایت میل میکند برابر بینهایت است و زمانی ...
تابع لگاریتمی
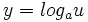
توابع لگاریتم در پایه محاسبه ی قواعد حاکم بر توابع لگاریتمیمشتق آهنگ های نسبی رشد توابع لگاریتم در پایه همچنین ببینید: توابع لگاریتم در پایه می دانیم که اگر عدد مثبتی به جز یک باشد، تابع مشتق پذیر و یک به یک است. علاوه بر این، مشتق آن یعنی ، هرگز صفر نمی شود. پس این تابع یک معکوس مشتق پذیر دارد که آن را " لگاریتم در پایه ی " نامیده و با نشان می دهند. چون و معکوس یکدیگرند، ترکیب آن ها به هر ترتیبی، تابع همانی است. پس روابط زیر به دست می آیند: بنابر این لگاریتم در پایه ی ، نمایی است که باید به توان آن برسد تا به دست آید. محاسبه ی عدد را همیشه میتوان به کمک فرمول زیر از لگاریتم های طبیعی و به دست آورد: این فرمول را می توان با روش زیر استنتاج کرد: قواعد حاکم بر توابع لگاریتمی الف)ب)ج) مشتق اگر تابع مشتق پذیری از باشد، آنگاه: چرا که: آهنگ های نسبی رشد توابع ممکن است توجه کرده باشید که توابع نمایی نظیر و ، وقتی بزرگ می شود، خیلی سریع تر از چند جمله ای ها و توابع گویا رشد می کنند. به ویژه این توابع نمایی خیلی سریع تر از تابع صعود خواهند کرد و وقتی زیاد می شود، بیش از فزونی می گیرد. در واقع وقتی ، توابع و تندتر از هر توان مثبتی از ، رشد می کنند. در مقابل، توابع لگاریتمی نظیر و ، که معکوس توابع و می باشند، وقتی ، از هر توان مثبتی از رشد کمتری دارند. به عنوان مثال اگر محور ها را با سانتیمتر مدرج کنیم، باید روی محور به اندازه ی چهار سال نوری جلو برویم تا نقطه ای بیابیم که به ازای آن ارتفاع نمودار تنها بشود. توجه: هر دو تابع لگاریتمی و ، وقتی ، با یک آهنگ رشد می کنند چرا که: و این حد همیشه متناهی و مخالف صفر است. لگاریتم در پایه لگاریتم های در پایه ، که غالبا " لگاریتم های معمولی " نامیده می شوند، در بسیاری از فرمول های علمی ظاهر می گردند. مثلا"، شدت زمین لرزه که بر حسب ریشتر گزارش می شود، دارای فرمولی به شرح زیر است: که در آن دامنه حرکت زمین بر حسب میکرون در ایستگاه گیرنده، دوره تناوب موج زلزله بر حسب ثانیه و ثابتی تجربی است که میزان تضعیف موج زلزله را با زیاد شدن فاصله از مرکز زمین لرزه نشان می دهد. یا مقیاس برای اندازه گیری قدرت اسیدی یک محلول، مقیاسی لگاریتمی است. مقدار ( یعنی پتانسیل هیدروژن ) محلول، لگاریتم طبیعی عکس غلظت یون هیدرونیم، است. نکته ای در مورد نماد گذاری: در بیشتر کتاب های درسی و ماشین حساب ها از ، برای نمایش استفاده می کنند. جدول انتگرال توابع لگاریتمی:
نکات آموزشی تابع نمایی ولگاریتم
بسمه تعالي نكات كمك آموزشي تابع نمايي وتابع لگاريتم رياضي2 تابع نمايي: به توابعي باضابطه ي f(x)=ax كه درآنa ،عددي مثبت ومخالف صفر است ،تابع نمايي گوييم (به وضوح ميتوان ديد تابع نمايي كه تابعي همواره مثبت است . نمودار تابع y=ax باشرط 1 <a به صورت روبه رو است : ونمودار تابع y=ax با شرط 1 > a > 0 به صورت مقابل مي باشد. نكته :صعود ونزول در توابع نمايي 1) در تابع y=ax با شرط 1 < a ،با افزايش x، مقدار تابع هم زياد مي شود مثال - براي تابع x 2 = y داريم : 2) در تابع y=ax با شرط 1 >a > 0 با افزايش مقدار x ، مقدار تابع كم مي شود مثال – براي تابع داريم: 15 <17 دامنه وبرد توابع نمايي: درتابع نمايي f(x)=ax ، x هرمقدار حقيقي مي تواند باشدوبا توجه به نمودار به وضوح مقدار تابع هر عدد حقيقي مثبت مي تواند باشد پس دامنه وبرد : و به طور مثال برد تابع 1 y= 2x+1+ خواهد شد: 1<y 1 < 1+ x+1 2 0< x+1 2 0< x 2 نامساوي ميانگين هندسي وحسابي : دونامساوي زير كه به نامساوي ميانگين حسابي وهندسي مشهور هستند در محاسبه برد توابع نمايي كاربرد زيادي دارند . 2 ≤a + b 0≤bو0≤a (1 2- ≥ a+b 0≥b و 0 ≥ a (2 مثال: برد تابع –x+3 2 + x+1 2 = f(x) راحساب كنيد. ( و8]= 2≤ -x+32 + x+1 2 تعريف لگاريتم : تابع نمايي xa =y يك تابع يك به يك است بنابراين وارون پذير است .وارون اين تابع ، تابع لگاريتم نام دارد وبه صورت مي باشد. نكته: چون لگاريتم يك تابع يك به يك است داريم: قانون تغيير مبنا: يكي از قوانين مفيد لگاريتم قانون تغيير مبنا ست . نتيجه1: درحالت خاص 10=c به تساوي مي رسيم. نتيجه2: با استفاده از نتيجه 1 داريم: نتيجه3: با تركيب قانون ونتيجه 1 به دست مي آوريم: مثال: مقدار را حساب كنيد. نكته: ...
تابع لگاریتم وقواعدمربوط به لگاریتم(دوم تجربی - ریاضی)
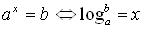
در این درس از ریاضیات به آموزش قواعد و فرمول های مربوط به تابع لگاریتم می پردازیم: تابع لگاریتم:تابع لگاریتم یکی از توابع غیر جبری در ریاضیات است,در مورد این تابع برخی قواعد است که آموختن و به کار گیری آن ها شما را در حل مسائلی که در آن ها لگاریتم موجود است یاری می کند. عبارت زیر یکی از قواعد مهم لگاریتم است که ارتباط بین حاصل یک عبارت توان دار و لگاریتم را بیان می کند: لگاریتم حاصلضرب را می توان با استفاده از روش زیر به لگاریتم جمع تبدیل نمود: لگاریتم تقسیم دو عبارت را می توان با استفاده از روش زیر به تفریق تبدیل کرد: لگاریتم توان دار: لگاریتم 1 برابر صفر می باشد. لگاریتم هر عدد با مبنای همان عدد برابر 1 می باشد: هرگاه مبنای لگاریتم 10 باشد می توانیم 10 را که مبنای لگاریتم است ننویسیم
ریاشی
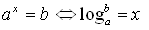
مجانب قائم چیست-آموزش ریاضیات پایه-تعریف مجانب قائم Published April 7, 2010 | By admin آموزش ریاضیات:مجانب قائم چیست؟ تعریف مجانب قائم:مجانب قائم خطی است عمودی که در کنار منحنی حرکت می کند و در بی نهایت بر آن مماس می شود.مجانب قائم خطی موازی محور Y هاست. آموزش ریاضیات,مجانب قائممجانب قائم در چه توابعی موجود است؟ مجانب قائم در توابع کسری موجود است.با این حساب در جاهایی که مخرج کسر صفر می شود مجانب قائم وجود دارد. روش بدست آوردن مجانب قائم: برای بدست آوردن مجانب قائم تابع معادله مخرج کسر برابر با صفر را حل می کنیم.به عبارتی دیگر ریشه های مخرج را بدست می آوریم. آموزش ریاضیات,ریشه های قابل قبول برای مجانب قائمریشه های مخرج مجانب های قائم هستند اما به شرطی که این ریشه ها صورت کسر را صفر نکنند. همچنین ریشه های مخرج در صورتی که زیر رادیکال فرجه زوج را منفی کنند,به عنوان مجانب قائم قابل قبول نیستند. تهیه شده توسط آبشاران دات کام دکوراسیون منزل دکوراسیون داخلی دکوراسیون آشپزخانه دکوراسیون سامسونگ ترانزیستور چیست تست تمرکز و سرعت عمل رله انواع رله رله چیست مدار الکتریکی دوربین دیجیتال الکتروسکوپ یا برق نما چیست Posted in مجانب قائم|مجانب افقی|مجانب مایل | Tagged آموزش ریاضیات, مجانب قائم, مجانب قائم چیست آموزش مثلثات-تابع تانژانت و نمودار تانژانت Published March 30, 2010 | By admin آموزش مثلثات و ادامه ی توابع مثلثاتی:تابع تانژانت tan نیز یکی دیگر از توابع فرد مثلثاتی است که نمودار آن نسبت به مبداء مختصات قرینه است.تابع تانژانت برابر حاصل تقسیم سینوس بر Cos می باشد.این تابع مثلثاتی نیز مانند سینوس و Cos یک به یک نیست.برد تابع مثلثاتی تانژانت مجموع ی اعداد حقیقی است. درمورد تانژانت نیز رابطه ی زیر برقرار است: Y=Tan(-x)=-Tan(x) تهیه شده توسط آبشاران دات کام دکوراسیون منزل دکوراسیون داخلی دکوراسیون آشپزخانه دکوراسیون سامسونگ ترانزیستور چیست تست تمرکز و سرعت عمل رله انواع رله رله چیست مدار الکتریکی دوربین دیجیتال الکتروسکوپ یا برق نما چیست Posted in آموزش مثلثات و دایره مثلثاتی, ریاضیات پایه|تابع های ریاضی | Tagged آموزش ریاضیات, آموزش مثلثات, تابع, تابع تانژانت, نمودار تانژانت آموزش ریاضیات-تابع مثلثاتی و نمودار تابع Published March 30, 2010 | By admin آموزش مثلثات,در ادامه ی آموزش ریاضیات و مبحث مثلثات: تابع مثلثاتی Cos نیز یکی از توابع مهم مثلثاتی است.همانطور که از نمودارد تابع مثلثاتی Cos پیداست,این تابع یک تابع زوج است (نسبت به محور Y قرینه است).دامنه ی تابع مثلثاتی Cos مجوعه ی اعداد حقیقی و برد این تابع مثلثاتی اعداد بین 1 و 1- می باشند.یعنی مقدار از ...
قواعد مشتق گیری توابع
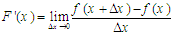
هرگاه بخواهیم از تابع f(x) مشتق بگیریم,مشتق این تابع به صورت زیر تعریف می شود: همچنین برای محاسبه ی مشتق تابع در نقطه ای خاص که شیب خط مماس در آن نقطه می باشد از رابطه ی زیر استفاده می شود. زاویه ی بین نیم مماس ها نیز از رابطه ی زیر محاسبه می شودکه در آن L1 و L2 مقادیر مشتق چپ و راست نقطه ی مورد نظر می باشند: نکات مهم مشتق گیری توابع : در این قسمت از آموزش ریاضیات با نکات مهمی در مشتق گیری آشنا می شوید: برای مشتق گرفتن از توابع قدر مطلق و جزء صحیح در نقطه ای خاص ابتدا باید علامت قدر مطلق و جزء صحیح را از بین ببریم سپس اقدام به مشتق گیری نماییم. مشتق عامل صفر: هرگاه یک تابع به نام f(x) داشته باشیم و مشتق این تابع را از ما بخواهند و f(x)=0 باشد فقط از علملی که صفر شده است مشتق می گیریم و باقی عبارات را عینا می نویسیم. اگر تابعی پیوستگی راست داشته باشد می تواند مشتق راست داشته باشد(ممکن است مشتق راستی در کار نباشد) اگر تابعی پیوستگی چپ داشته باشد می تواند مشتق چپ داشته باشد.(اما ممکن است مشتق چپی در کار نباشد) اگر تابعی فاقد پیوستگی راست و پیوستگی چپ باشد,این تابع مشتق راست و مشتق چپ نیز نخواهد داشت.قبل از گرفتن مشتق راست و مشتق چپ نوع پیوستگی بایستی بررسی شود. مشتق گیری ازتوابع مثلثاتی وقدرمطلق : مشتق توابع مثلثاتی: در این بخش از سری آموزش های مشتق گیری در ریاضیات به مبحث مشتق توابع مثلثاتی و توابع معکوس مثلثاتی و تابع قدر مطلق می پردازیم: برای محاسبه ی مشتق توابع مثلثاتی از روابط ذیل استفاده می شود: برای محاسبه ی مشتق توابع معکوس مثلثاتی از روابط زیر استفاده می شود مشتق گیری از تابع قدر مطلق : برای محاسبه ی مشتق تابع قدر مطلق می توانید از تابع زیر استفاده نمایید: در این قسمت از سری آموزش های ریاضیات,به آموزش و نکات مشتق و مشتق گیری می پردازیم: هنگامی که از شما مشتق تابعی خواسته می شود شما بایستی با استفاده از اطلاعاتی که از قبل در مورد آن تابع و مشتق آن تابع در دست دارید مشتق آن تابع را محاسبه نمایید.گاهی اوقات در برخی روابطی که به شما داده می شود یک یا چند تابع ترکیب شده اند که شما برای محاسبه ی مشتق آن بایستی برخی قواعد مشتق گیری را که در اینجا می آموزید رعایت نمایید. در عمل مشتق گیری ابتدا کار ضریب و توان را انجام می دهیم. توضیح:یعنی قبال از هر کاری بهتر است که ابتدا تکلیف مشتق ضریب و توان تابع را مشخص کنید. مشتق عبارت توان دار از فرمول زیر بدست می آید. مشتق عبارات کسری از فرمول زیر بدست می آید: مشتق دو عبارت که در هم ضرب شده اند از فرمول زیر حساب می شود: مشتق توابع رادیکالی از فرمول ذیل بدست می آید: فرمول هاي مشتق تابع مشتق شرايط ...
طرح درس ریاضی دوم دبیرستان
طــرح درس ســالانــه درس: ریاضی 2 پایه : دوم متوسطه سال تحصیلی : 89-88 محدوده زمانی : نیمسال اول تعداد جلسات در هفته : 2 جلسه ماه هفته جلسه فصل موضوع درس اهداف و مجموعه فعالیت های آموزشی صفحات کتاب مهر اول 1 اول الگو و دنباله آشنایی با مفهوم دنباله – نوشتن جمله عمومی دنباله با داشتن جمله های آن و برعکس 2تا 5 2 اول دنباله حسابی حل مسائل صفحه 5 و 6 - آشنایی با مفهوم دنباله حسابی - نوشتن جمله عمومی برحسب قدرنسبت و جمله اول 5 تا 9 دوم 3 اول دنباله هندسی حل مسائل صفحه 9و 10 - آشنایی با مفهوم دنباله هندسی – نوشتن جمله عمومی برحسب قدرنسبت و جمله اول 9تا 12 4 اول نزدیک شدن جمله های دنباله به یک عدد- دنباله تقریبات اعشاری حل مسائل صفحه 12 و 13- آشنایی با مفهوم گرایش جملات یک دنباله به یک عدد – محاسبه برخی مقادیر تقریبی 13تا16 سوم 5 اول ریشه گیری اعداد حقیقی – توان رسانی با توان گویا حل مسائل صفحه 16- آشنایی با محاسبه مقادیر تقریبی اعداد با توان کسری – آشنایی با نمادهای مربوط 16تا 21 6 اول توان رسانی با توان حقیقی حل مسائل صفحه 21- آشنایی با محاسبه مقادیر تقریبی اعداد با توان رادیکالی – حل مسائل صفحه 23و24 21تا 24 چهارم 7 دوم ارزشیابی مرحله ای سنجش میزان یادگیری و تثبیت آن آزمون از فصل اول 8 دوم مفهوم رابطه و تابع آشنایی با مفهوم تابع –طرق مختلف نمایش تابع – مفهوم رابطه – شرط تابع بودن یک رابطه 26تا31 آبان اول 9 دوم دامنه و برد توابع حل مسائل صفحه 31 تا 34 حل تمرین در کلاس صفحه 36 31تا 36 10 دوم نام گذاری توابع آشنایی با نام گذاری توابع - آشنایی با توابع خطی حل مسائل صفحه 40 37 تا 40 دوم 11 دوم وارون یک رابطه- توابع یک به یک آشنایی با مفهوم وارو ن رابطه و تابع - آشنایی با مفهوم یک به یک بودن تابع و وارون پذیری آن 41تا46 12 دوم بازه – مقدارتابع در یک نقطه – نمایش جبری یادآوری مفهوم بازه – محاسبه مقدارتابع – نمایش جبری تابع 46تا 51 سوم 13 دوم ------------ حل مسائل صفحه 51تا 54 51تا 54 14 دوم ارزشیابی مرحله ای سنجش میزان یادگیری و تثبیت آن آزمون از فصل دوم چهارم 15 سوم تابع همانی - تابع ثابت - تابع قدر مطلق آشنایی با توابع همانی ،ثابت و قدرمطلق و نحوه رسم نمودار این توابع 56تا 62 16 سوم رسم نمودار برخی از توابعدرجه دوم به کمک انتقال تابع آموزش نحوه رسم نمودار توابع با بهره گیری از انتقال 62تا 64 آذر اول 17 سوم توابع گویا آشنایی با توابع گویا ( شامل عبارات کسری ) و توجیه دامنه این توابع 64تا 66 18 سوم توابع رادیکالی آشنایی با توابع ...
توان ،رادیکال،لکاریتم
مثال1: سایه سنگین آموزش اعداد طبیعی و چهار عمل اصلی آن در دوره ابتدایی و مقدماتی نظام آموزش و پرورش ایران چنان می باشد که بیان و معرفی سایر اعداد (صحیح وگویاو...)در سنوات بعد کاری بس دشوارهم برای معلم وبه طبع آن یاد گیری و پذیرش آن برای متعلم می باشد. دانش آموز چنان در بحر اعداد طبیعی غرق می شود که گویی اعداد دیگر خود ساخته ¸فرعی ¸ وغیرضروری می باشند.واین روند در ادامه بحث های ریاضی (جبر¸ حسابان ¸مثلثات ....)به یک چالش تبد یل می شود. هنوزاز شوک اینکه حاصل (5-3) رانیز به حساب آورد در نیامده که ما اعداد گنگ و در کل اعداد حقیقی را به او معرفی خواهیم کرد. از طرفی بیان ومعرفی اعداد حقیقی در ابتدای کار آموزش اعداد امری بیهوده و غیرممکن است.ونظریه از کل به جزء گفتن در این مورد فقط ای کاش می شد می خواهد وبس. یکی از راه حلهای رفع این مشکل به نظر آن است که درهر دوره آغازین تحصیلی در ریاضی (بحث های حسابی وجبرو...) یاد آوری ومعرفی اعداد خوانده شده و متذکر شدن بر این نکته که اعداد د یگری غیر ا ز اینها نیز وجود دارد. همچنین تمرین اعمال جبری اصلی و فرعی مربوط به آن مجموعه ها نیز امری لازم و ضروری می باشد. مثال2:ای کاش می شد در شروع آموزش درس توان موضوع عکس عمل توان (ریشه گیری )و همچنین وابستگی لگاریتم به آن را با هم مطرح می ساختیم و پابه پای تمرینات توان وابسته به قواعد و روش های آن ریشه گیری و لگاریتم رانیز تمرین می کردیم. این گسست آموزش باعث می شود که دانش آموز نتواند بین این مفاهیم ارتباط برقرار کند وبه همین خاطر درسهای ریشه گیری و لگاریتم را سخت پندارد ونیز رغبتی به یاد گیری آنها و قواعد آن ها نداشته باشد. بهتر است سری به کلاس تخیلی بزنیم. معلم: بچه ها توجه کنید:یاد تونه گفتیم 7 3 =7+7+7 یعنی به جای اینکه سه بار عدد 7 را با هم جمع کنیم کافی بود عدد 3 را در آن ضرب کنیم . یعنی عمل ضرب به داد عمل جمع رسیدواگر می خواستیم 20 7 را بنویسیم یا باید هفت بار 20 را با هم جمع می کردیم یا اینکه بسیت بار عدد7را . آره عمل توان نیز به کمک ضرب آمد تا از دو باره نویسی ضرب جملات تکراری جلو گیری شود. پس گفتیم به جای 10 10 10 می توان 103 را نوشت . 1000 =103=10 10 10 دانش آموز : عدد 3 چه نسبتی با 1000 و 10 دارد؟ معلم : سوال خوبی پرسیدی اما بگذار تا ریشه و توان را بیشتر توضح دهیم بعد به سئوال شما هم می رسیم . ( سر آغاز لگاریتم ) بله بچه ها داشتیم می گفتیم که 1000 توان سوم 10 است و آن را آن به صورت یک تساوی از 103 =1000 نمایش می دهیم.و 10و نیز ریشه سوم 1000 می باشد.که برای نمایش آن به صورت یک تساوی ...
