فرمول های لگاریتم
فرمول های لگاریتم
فرمول های لگریتم را به صورت یکجا از لینک زیر دانلود کنید فرمول های لگاریتم منبع :mathخونه
فرمولهای لگاریتم
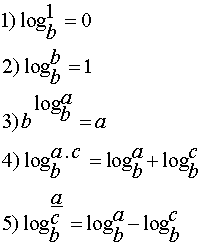
مجموعه فرمول های لگاریتم
این مجموعه شامل فرمول های مربوط به مبحث لگاریتم است مخصوص دروس ریاضی ۲ و ریاضی چهارم انسانی لینک دانلود
لگاریتم
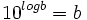
مقدمه در جبر عموما لگاریتم معمولی یا لگاریتم در پایه 10 عدد b را توانی تعریف میکنند که 10 باید به آن برسد تا b بدست آید: . فرض کنیم چنین عددی موجود بوده و از لگاریتمها برای سادهکردن ضرب اعدادی که ارقام اعشاری زیادی دارند استفاده میکنیم. تعریف تابع لگاریتم طبیعی بصورت زیر نمایش داده میشود: به ازای هر x بزرگتر از 1 ، این انتگرال مساحت ناحیهای را نشان میدهد که از بالا به خم از پایین به محور t از طرف چپ به خط t=1 ، و از طرف راست به خط t=x محدود است. تاریخچه در اواخر قرن شانزدهم یک بارون اسکاتلندی به نام جان نپر (1550-1617) ابزاری بنام لگاریتم ابداع کرد که با تبدیل ضرب به جمع کار محاسبه را ساده میکند؛ یعنی داریم: لگاریتم x + لگاریتم a = لگاریتم ax برای ضرب دو عدد مثبت x,a از یک جدول ، لگاریتمهای x,a را پیدا میکنیم، سپس این لگاریتمها را بهم میافزائیم مجموع حاصل را در داخل جدول مییابیم، و بالاخره حاصلضرب مطلوب ax را از حاشیه جدول میخوانیم. مسلما در دست داشتن جدول کلید کار بود، به همین سبب نپر در دو دهه آخر زندگیاش را صرف تهیه جدولی کرد که هیچگاه نتوانست آن را تمام کند. و این در حالی بود که تیکو براهه ستاره شناس ، مشتاقانه در انتظار این جدول بود تا میتواند محاسبات خودش را تسریع بخشد مشتق تابع لگاریتم طبیعی چون تابع با انتگرال ذکر شده در قسمت تعریف ، تعریف میشود، فورا از نخستین قضیه اساسی حساب دیفرانسیل و انتگرال نتیجه میشود که مشتق تابع برابر خواهد بود. بنابراین اگر u تابع مشتقپذیری از x باشد، آنگاه از قاعده زنجیری داریم: فرمول کلیتر زیر بدست میآید: مشتقگیری لگاریتمی گاهی یک تابع با معادلهای پیچیده داده شده با گرفتن لگاریتم از طرفین آن پیش از مشتقگیری میتوان مشتقش را سریعتر حساب کرد. خواص قلمرو: مجموعه تمام اعداد حقیقی مثبت ، x>0 برد: مجموعه تمام اعداد حقیقی این تابع بر قلمرو خود پیوسته و صعودی است هر گاه آنگاه . این تابع یک تابع یکبهیک از قلمرو خود به بردش است، بنابراین دارای معکوس است. حاصلضرب ، خارج قسمت و توان: هر گاه x,a دو عدد مثبت باشند. آنگاه:معکوس تابع لگاریتم چون یکبهیک و مشتقپذیر است، دارای معکوس مشتقپذیر میباشد نمودار منعکس نمودار تابع نسبت به خط y=x است. این نمودار تابع نیز میباشد. تابع به ازای هر عدد حقیقی x مساوی میباشد. تابع حاصل تابع مشتق پذیری از x است که به ازای هر x حقیقی تعریف شده است و بعنوان تابع نمایی از آن یاد میشود که e را پایه و x نما خوانده میشود. همچنین توجه میکنیم که حد تابع نمایی زمانی که x بسمت بینهایت میل میکند برابر بینهایت است و زمانی ...
دانلود فرمولهای لگاریتم
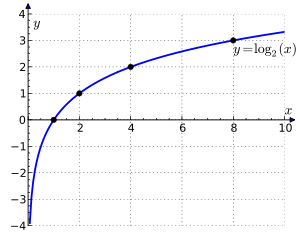
فرمول های لگاریتم کلیه فرمول ها و قوانین لگاریتم را در ادامه دانلود نمایید. این فایل آموزشی می تواند مورد استفاده دانش آموزان و داوطلبان کنکور قرار گیرد. فرمت فایل: pdf حجم فایل: ۸۰ کیلوبایت دانلود: دانلود فرمول های لگاریتم| لینک کمکی منبع: ریاضی سرا مشاهده ی مطالب زیر را نیز به شما پیشنهاد می کنیم: ۱۸ سال با لگاریتم لگاریتم و کاربردهای آن در زندگی فرمول های ریاضی فرمول های مثلثات گاج MathType v6.9 – نرم افزار تایپ معادلات و فرمول های پیچیده ی ریاضی
معکوس توابع هیپر بولیک
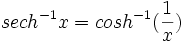
اتحادهای مفید فرمول های لگاریتمی برای محاسبه ی توابع هیپربولیک معکوس مشتق ها و انتگرال ها محدودیت های و در فرمول های مشتق و از محدودیت هایی طبیعی ناشی می شود که در مورد مقادیر تانژانت و کتانژانت هیپربولیک وجود دارد. وقتی فرمول های مشتق را معکوس می کنیم تا فرمول های انتگرال به دست آیند، تمایز بین و اهمیت پیدا می کند زیرا در غیر این صورت نمی توانیم بگوییم که انتگرال عبارت است از یا . فرمول های انتگرال گیری زیر مستقیما از معادله های و نتیجه می شوند. انتگرال های مذکور در فرمول های و و و را با جانشینی های مثلثاتی نیز می توان به دست آورد و انتگرال موجود در فرمول به روش تجزیه به کسرهای ساده قابل محاسبه است.
توابع نمایی در ریاضی
کشف لگاریتم: مقدمه نظريه ها و قاعده هاي رياضي، با کشف خود «هستي» پيدا مي کنند، آن ها تنها وجود دارند و اغلب بدون کاربردند. دير يا زود، و گاهي بعد از صدها و هزارها سال، اين موجودات رياضي به «صفت» تبديل مي شوند و کاربرد خود را در زندگي و عمل، در ساير دانش ها، در صنعت و هنر پيدا مي کنند. «اويلر» شايد کسي فکر نمي کرد لگاريتمي که در رابطه با نياز محاسبات عملي کشف شد در آينده کاربردهاي وسيعي پيدا کند. با ورود لگاريتم به دنياي رياضيات و آشنا شدن مردم و دانشمندان با آن، اين شاخه کاربردهاي زيادي را در زندگي روزمره پيدا کرد. چنانکه امروزه لگاريتم در حسابداري و در تعيين بهره ي مرکب و نيز مسائل مالي کاربرد فراواني يافته است. همان زمان که لگاريتم اختراع شده بود اويلر رابطه ي بين عدد e و بهره ي مرکب را دريافت و فهميد که حد بهره به سمت عددي متناسب (يا مساوي در شرايط خاص) ، که همان عدد e است ميل مي کند. همچنين از لگاريتم در مدلسازي و بازار يابي سهمي استفاده مي شود. مدلسازي ايجاد الگو و تمثيلي براي تجسم واقعيت هاي خارجي است که در مسائل مربوط به رياضيات و حسابداري کاربرد دارد لگاريتم به توان رساندن داراي 2 عمل معکوس مي باشد. اگر a=c در اين صورت پيدا نمودن a يعني استخراج ريشه يکي از دو عمل معکوس مي باشد و پيدا نمودن b يعني لگاريتم گيري عمل معکوس ديگر است. لگاريتم به چه منظوري اختراع شده است؟ بديهي است که تا نياز به چيزي احساس نشود آن چيز کشف و اختراع نمي گردد، در واقع هرکدام از علومي که با آن روبه رو هستيم هريک به مقتضاي نيازي و با توجه به هدف خاصي پيکر بندي شده اند. لگاريتم نيز با توجه به محاسبه هاي طولاني و ملال آوري که دانشمندان سده هاي شانزدهم و هفدهم ميلادي با آن سر و کار داشتند، بوجود آمد. اين محاسبه ها وقت و نيروي زيادي را از دانشمندان تلف مي کرد و هميشه دانشمندان در ذهن داشتند که چطور مي شود بدون انجام چنين محاسبات پيچيده و دشواري و آن هم در کمترين زمان ممکن به جواب مطلوب دست يابند. گفته مي شود که حتي در قرن هشتم هندي ها با محاسبات مربوط به لگاريتم آشنايي داشتند اما اين کلمه و مفهوم مربوط مي شود به قرن شانزدهم .جدول هايي نيز در اين زمينه بوجود آمد و شايد همين تلاش ها و نيازها بود که سر انجام به کشف لگاريتم انجاميد تا آن جا که دو دانشمند به طور همزمان و بدون اينکه از کار يکديگر آگاه باشند موفق به کسب چنين افتخاري گشتند اولي جان نپر و ديگري بورگي. اما اصطلاح لگاريتم نشات گرفته از فعاليت هاي نپر است که از واژه ي يوناني «لوگوس» به معني نسبت و «ارتيوس» به معني عدد گرفته شده است. او همچنين بجاي لگاريتم از اصطلاح عدد ساختگي ...
لگاریتم (2)

پیشینه پیشینیان ویراسنا، ریاضیدان هندی از کسانی بود که با مفهومی به نام ardhaccheda کار کرد. ardhaccheda یعنی تعداد دفعاتی که میتوان ۲n را نصف کرد. برای نمونه برای توانهای دقیق ۲ این کار برابر با لگاریتم گرفتن در مبنای ۲ بود؛ وی همچنین لگاریتم در پایهٔ دیگر اعداد صحیح مانند لگاریتم در پایهٔ ۳ (trakacheda) و در پایهٔ ۴ (caturthacheda) را نیز معرفی کرد.]مایکل استیفل در سال ۱۵۴۴ میلادی در نورنبرگ Arithmetica integra را منتشر کرد، در این نوشته جدولی از اعداد صحیح و توانهای ۲ داده شده بود، این جدول به عنوان نسخهٔ اولیهٔ جدول لگاریتم شمرده میشود. از نپر تا اویلر جان نپر (۱۶۱۷-۱۵۵۰) بدست آورندهٔ روش لگاریتمگیری روش لگاریتمگیری در سال ۱۶۱۴ از سوی جان نپر در کتابی با عنوان Mirifici Logarithmorum Canonis Descriptio (توصیفی بر قانون شگفتانگیز لگاریتم) ارائه شد.همچنین ژو بورجی (به فرانسوی: Joost Bürgi) نیز جداگانه روش لگاریتمگیری را پیدا کرده بود اما آن را شش سال پس از نپر منتشر کرد. نپر، با استفاده از روش تقسیمهای متوالی توانسته بود عبارت را به ازای Lهای میان ۱ تا ۱۰۰ محاسبه کند. جواب این عبارت برای ۱۰۰ = L تقریبا برابر است با ۰٫۹۹۹۹۹ = ۱ - ۵-۱۰ و ۲۰ ۰٫۹۹۵ ≈ ۰٫۹۹. این محاسبات که ۲۰ سال طول کشید، باعث شد تا او بتواند به ازای هر عدد N در بازهٔ ۵ تا ۱۰ میلیون، بتواند عدد L را پیدا کند که در رابطهٔ زیر صدق کند: نپر ابتدا نام «عدد ساختگی» را بر L نهاد ولی پس از مدتی واژهٔ «لگاریتم» logarithm را معرفی کرد و آن را بر عددی گذاشت که نمایندهٔ یک نسبت است: واژهٔ λόγος برابر logos به معنی «نسبت» است و واژهٔ ἀριθμός برابر arithmos به معنی «عدد» است. بوسیلهٔ عبارت زیر میتوان مفهوم پیشین لگاریتم را با مفهوم امروزی لگاریتم طبیعی مرتبط کرد: با تقریب خوبی داریم: این دستآورد خیلی زود مورد تحسین گستردهٔ دیگران قرار گرفت، به همین دلیل با تلاش دانشمندانی چون بوناونتورا کاوالیری (Bonaventura Cavalieri) از ایتالیا، ادموند ونگت (Edmund Wingate) از فرانسه، زو فنگزوئو (Xue Fengzuo) از چین و... مفهوم لگاریتم همه جا فراگیر شد. هذلولی y = ۱/x (منحنی قرمز) و سطح زیر آن از x = ۱ تا ۶ (قسمت نارنجی رنگ). در سال ۱۶۴۷ گرگوآر دو سن-ونسان توانست مفهوم لگاریتم را با یک چهارم هذلولی مرتبط کند، با فرض آنکه سظح زیر منحنی هذلولی به ازای ۱ = x تا t در رابطهٔ زیر صدق میکند: لگاریتم طبیعی اولین بار از سوی نیکولاس مرکاتور در مقالهٔ Logarithmotechnia که در سال ۱۶۶۸ منتشر کرد، توضیح داده شد. البته پیش از او جان اسپیدل که یک معلم ریاضی بود در سال ۱۶۱۹ جدولی از لگاریتم طبیعی را گردآوری کرده بود. در حدود سال ۱۷۳۰ لئونارد اویلر تابع نمایی ...
