فرمول نرخ رشد جمعیت
جدیدترین آمار جمعیت ایران
فارس: بر اساس برآوردی که مرکز آمار ایران انجام می دهد، جمعیت ایران در ساعت 8 و 36 دقیقه صبح روز پنج شنبه 14 بهمن ماه سال 1389 هجری شمسی از مرز 75 میلیون نفر گذشته است.بنابراین گزارش، اواخر سال گذشته بود که جمعیت ایران 74 میلیون نفری شده بود و در کمتر از یک سال یک میلیون نفر به جمعیت کشور اضافه شده است.نرخ رشد جمعیت ایران در حال حاضر 0.015 است.مرکز آمار ایران هر لحظه جمعیت ایران را بر اساس یک فرمول مشخص برآورد می کند که با عنوان ساعت جمعیتی در سامانه درگاه ملی آمار نشان داده می شود.بر اساس این گزارش، محاسبه جمعیت کشور بر اساس رابطه رشد به صورت زیر انجام می گیرد:رابطه رشد عبارت است از: Pn=P0(1+r)nکه در آن Pn پیش بینی جمعیت میانه سال 1390 و P0 جمعیت سرشماری سال 1385 و r رشد جمعیت سالانه کشور است که حدوداً برابر با 0.015 می باشد.
مدل های پیش بینی جمعیت
باسمه تعالی مدل های پیش بینی جمعیت در برنامه ریزی شهری : اساس مطالعات شهری- منطقه ای و فضایی را بررسی های جمعیتی در شاخص های مختلف جمعیت در گذشته ، حال و آینده تشکیل می دهد . بنابراین پیش بینی جمعیت در برنامه ریزی اقتصادی ،اجتماعی ، کالبدی و ... اولین گام در برنامه ریزی است . برای برآورد جمعیت مدل های مختلفی وجود دارد : از انواع مختلف مدل های جمعیتی هر کدام ویژگی های خاص خود را دارند که انتخاب نوع مدل و استفاده از آن در درجه اول به اطلاعات موجود در زمان و سپس به هدف برنامه ریزی بستگی دارد . مدل های جمعیتی به طور کلی به دو دسته روش های تجمعی و روش های ترکیبی قابل تقسیم هستند : 1-روش های تجمعی این روش ها که برای برآورد کل جمعیت ناحیه مورد مطالعه به کار می روند عبارتند از : مدل رشد خطی مدل رشد نمایی مدل رشد نمایی تعدیل شده مدل رشد نمایی مضاعف مدل منحنی لجستیک مدل مقایسه ای مدل رگرسیون خطی ساده مدل رگرسیون چند متغیره روش تناسبی مدل رشد خطی (The Linear Growth Model) این مدل الگویی از رشد جمعیت را توصیه می کند که در آن میزان جمعیت همچنان با نرخ فعلی خود تغییر می کند. (روند رشد جمعیت به صورت تابعی از رشد ثابت جمعیت در گذشته و وضع موجود در نظر گرفته می شود.) به همین ترتیب میزان تراکم جمعیت متناسب با زمان، افزایش یا کاهش خواهد داشت. اگر میزان افزایش یا کاهش جمعیت در طول برابر با مشخصه a باشد، متعاقب آن، سطح جمعیتی در سال n ام برابر خواهد بود با: +na Pn: میزان جمعیت در زمان n : میزان جمعیت پایه n : دوره زمانی بر حسب (ماه، سال، نیمسال و …) a : میزان رشد در واحد زمان 1053025+ (1*174306) = 1401637 مدل نمایی مدل رشد خطی افزایش جمعیت شهر را نسبت به زمان سپری شده پیش بینی می کرد. در صورتی که این فرایند ممکن است به دور از واقعیت باشد و نرخ رشد جمعیت در طول زمان تغییر نماید، که در این صورت رشد جمعیت به طور شتابان افزایش می یابد. به عبارت دیگر تغییر جمعیت تابعی است از سطح جمعیت موجود، یعنی هر چه جمعیت بیشتر باشد، رشد آن نیز شتابان می گردد. (مقدار افزایش جمعیت بر اساس مدل نمایی متناسب با میزان جمعیت موجود است. به طوری که نسبت بین افزایش جمعیت و جمعیت کل، ثابت است ولی افزایش صعود می کند.) فرمول کلی مدل رشد نمایی به صورت زیر است: (1+r در این فرمول جمعیت در سال مقصد، جمعیت در سال مبداء ، r رشد سالانه جمعیت و n فاصله زمانی بین سال مبداء و سال مقصد می باشد. تغییر رشد جمعیت به صورت زیر خواهد بود: r= r نرخ تغییرات را به صورت درصدی از سطح جمعیت موجود نشان میدهد. توجه داشته باشید چون در فرمول دوم نرخ رشد به درصد محاسبه شده اگر بخواهیم از آن در فرمول اول استفاده کنیم، بایستی آن ...
روند تحوّلات و علل و عوامل عمده افزایش جمعیت در شهراردبيل
چکیده: شهرها و روند شهرنشینی در ایران از دهه های اخیر تحوّلات عظیمی را پشت سر گذاشته است بگونه ای که طی دهه های اخیر تعداد و جمعیت شهرها و توسعه فضایی آنها ابعاد بی سابقه ای یافته است. شهر اردبيل، به عنوان مرکز استان اردبيل از این تحوّلات دور نمانده و با توجّه به موقعیت ارتباطی آن و مهاجرتهای روستایی و عشایری در دهه های اخیر افزایش جمعیت بالایی داشته است. در مقاله حاضر علاوه بر مطالعه جمعیت و نرخ رشد آن علل و عوامل اصلی افزایش جمعیت در اردبيل و آینده نگری آن و زمان مضاعف شدن جمعیت برای سالهای 1385 و 1400 محاسبه شده است. واژه های کلیدی: جمعیت، تحولات جمعیت، شهرنشینی، شهر اردبيل، استان اردبيل، نرخ رشد جمعیت. مقدمه: شهر پدیده تاریخی و در عین حال جغرافیایی است، شهر ساخته و پرداخته دوران گذشته و حال می باشد و هر دوره تاریخی به نوعی در چشم انداز جغرافیایی آن اثر گذاشته و بالمآل تضادهایی در چهره جغرافیایی آن بوجود آورده است. این تضادها و تباین ها را نمی توان به تنهایی با شرایط مکانی شهر که زاده توپوگرافی شهری است در رابطه گذاشت، بلکه ساختار اقتصادی و اجتماعی حاکم بر حیات شهری را در آن نقشی است(فرید، 1373، ص17) همچنین شهر واحد جمعیتی است و جمعیت بگونه ای که در شهر استقرار یافته، باید مورد تشریح قرار گیرد. در برنامه ریزیهای شهری، جمعیت بعنوان اصلی ترین عامل توسعه محسوب می گردد و افزایش آن نه تنها موجب افزایش سطح مسکونی می شود بلکه نیازهای خاصی را نیز در ابعاد مختلف مطرح می سازد. آنچنان که ایجاد مجتمعهای بزرگ ورزشی، توسعه واحدهای حفاظتی و ایمنی، ایجاد فضاهای سبز، ایجاد بزرگراهها به منظور سهولت دسترسی و ایجاد مراکز گذراندن اوقات فراغت را ضروری می سازد. (زنجانی، 1369، ص 132) بر مبنای تعاریف فوق الذکر، در مقاله حاضر، روند تحوّلات جمعیت و نرخ رشد جمعیت شهر اردبيل طی سالهای 1375-1335 مدّ نظر قرار گرفته و علل و عوامل عمده رشد جمعیت مورد بررسی و پیش بینی و برآورد جمعیت شهر اردبيل برای سالهای 1385 و 1400 با سه پیش فرض انجام شده است. روند تحوّلات جمعیت و نرخ رشد آن میزان رشد جمعیت در هر ناحیه حاصل و نتیجه تحوّلات اجتماعی، اقتصادی، سیاسی در طول زمان می باشد و به عواملی همچون زاد و ولد، مرگ و میر، برون کوچی و درون کوچی هر جامعه ارتباط می یابد. (قدیری معصوم، 1377، ص310) بر اساس سرشماری عمومی سال 1335، جمعیت شهر اردبيل معادل ۶۵٬۷۴۲ نفر بوده و در طول دهه 1345-1335 به جمعیت شهر 20902 نفر افزوده شد و جمعیت شهر از نرخ رشدی معادل 4/4% برخودار بوده است. (جدول شماره1) طی سالهای 1345 تا 1355، تعداد 45334 نفر به جمعیت شهر اضافه شد و در سال 1355 جمعیت آن به ۱۴۷٬۸۶۵ نفر ...
آمار و مدل سازی
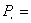
در این مقاله هدف ما،بررسی ساده ترین مدل جمعیت است.یعنی مدل جمعیت یک بعدی تعینی.(یعنی فرض می کنیم فقط یک نوع جمعیت باشد و در آن عوامل تصادفي موثر نیستند.) ما قبل از بیان فرمول مدل جمعیت، مثال زیر را مطرح می کنیم:مثال:متخصصان بر این باورند که زمین های قابل کشت وزرع، حداکثر می تواند غذای 40 میلیارد انسان را تامین کند،در آغاز سال 1990میلادی جمعیت جهان2/5میلیارد نفر تخمين زده شد . اگر جمعیت با میزان رشد ثابت 2% در سال افزایش یابد،در چه زمانی جمعیت به حداكثر میزان ذکر شده خواهد رسید؟ حل: 2/5 = جمعیت اولیه به میلیارد 02/0 = نرخ رشد= rجمعیت در سال میلیاردجمعیت در سال میلیاردجمعیت بعد ازn سال میلیارد حال قرار می دهیم: وn را با لگاریتم گرفتن از طرفین به دست می آوریم : در نتيجه : یعنی در سال 2093=103+1990 جمعیت به 40 میلیارد نفر می رسد.ما در این مثال، نرخ رشد جمعیت را سال به سال محاسبه کردیم.حال رشد جمعیت را در پايان هر ماه حساب مي کنیم،در مثال بالا نرخ رشد در ماه برابر با : می شود. جمعیت بعد از یک ماه میلیارد جمعیت بعد از دو ماه میلیارد جمعیت در سال 1991= میلیاردجمعیت بعد از n سال = میلیاردجمعیت در سال میلیارد حال اگر جمعیت را روز به روز محاسبه کنیم،نرخ رشد دریک روز برابر با: می شود. جمعیت بعد از یک سال میلیارد جمعیت بعد ازn سال= میلیارد جمعیت در سال 2093 برابر با : میلیارد می شود. حال اگر جمعیت را در هر ساعت محاسبه کنیم،نرخ رشد جمعیت در یک ساعت برابراست با: . جمعیت در سال 2093 برابر است با: اگر جمعیت را در هر ثانیه حساب کنیم،جمعیت در سال 2093 بیش تر می شود و به 799/40میلیارد نفر نزدیک می شود.برای دیدن علت این امر بهتر است به مطلب زیر توجه کنیم: دنباله ی را در نظرمی گیریم.این دنباله را برای مقدار های مختلف n محاسبه می کنیم: قضیه: موجود است و آن را عدد e مي ناميم . ...71828182/2=e حال فرض می کنیم نرخ رشد جمعیتr باشدو جمعیت اولیه را با و جمعیت بعد از tسال را با نشان مي دهیم.اگر جمعیت را سال به سال محاسبه کنیم: و و اگر جمعیت را در سال محاسبه کنیم: یعنی بعد ازt سال درصورتی که در هر سال، جمعیت را محاسبه کنیم،جمعیت به دو متغیر t (زمان) و n (تعداد تقسیمات زمان)بستگی دارد.بنابر این با نشان می دهیم: حال اگر n را بزرگ و بزرگ تر کنیم،یعنی محاسبه ی جمعیت را در مدت زمان های کوتاه تری انجام دهيم ،مدل ما به مدل واقعی جمعیت نزدیک و نزدیک تر می شود.یعنی اگر n را به سمت بی نهایت میل دهیم ،جمعیت در هر لحظه محاسبه می شود.این مدل را مدل پیوسته می نامیم و آن را با نشان می دهیم.یعنی: با فرض ،اگر آن گاه .بنابراین . ...
آیا مستندات علمی برای سیاست تشویق به رشد جمعیت وجود دارد؟
لطفاً روی این استدلال علمی کمی تأمل کنید دکتر محمدباقر نوبخت- معاون پژوهشهای اقتصادی مرکز تحقیقات استراتژیک مجمع تشخیص مصلحت نظام – به نقل از : آفتاب گفته شده است که سیاست فعلی کنترل جمعیت در ایران باید تغییر کند و برای این تغییر، استدلال علمی وجود دارد. زیرا؛ هماکنون بهطور متوسط تعداد افراد هر خانوار ایرانی کمتر از 4 نفر است، با توجه به اینکه در هر خانواده 2 نفر پدر و مادر هستند، پس تعداد فرزندان در هر خانواده ایرانی، بهطور متوسط کمتر از 2 نفر است، لذا سیاست فعلی کنترل جمعیت که بر پایه 2 فرزند برای هر خانواده تنظیم شده است باید تغییر کند. با عنایت به اینکه، از این تحلیل به عنوان یک استدلال علمی یاد شده و نتیجهگیری میشود که رشد جمعیت ایران باید افزایش یابد، ضروری است تا حداقل برای ثبت در تاریخ، توضیح داده شود که هم استدلال ارائه شده غیرعلمی است، هم نتیجهگیری آن مردود است و هم آثار اجرائی شدن چنین دیدگاهی برای کشور و نسلهای آتی میتواند بسیار زیانبخش باشد، زیرا: اولاً؛ شاخصی که برای تحلیل در این استدلال به اصطلاح علمی استفاده شده است، «بُعد خانوار» است. این شاخص که از تقسیم تعداد جمعیت به تعداد خانوار بدست میآید و صرفاً متوسط تعداد افراد در خانوار را نشان میدهد. (جمعیت/خانوار = بُعد خانوار) /بهطور مثال اگر در یک کشور با جمعیت ثابت، به دلیل تشکیل خانوارهای جدید ناشی از افزایش ازدواجها و شکلگیری زندگی مستقل، تعداد خانوارها افزایش یابد، شاخص «بُعد خانوار» کاهش مییابد و برعکس اگر در همین کشور به دلایل مختلف از جمله تراکم جمعیت افراد با سن کمتر از سن ازدواج، تشکیل زندگی و خانوادههای مستقل و در عمل تعداد خانوارها محدود باشد، شاخص «بُعد خانوار» عدد بزرگتری را نشان میدهد. در حالیکه از هیچیک از دو حالت، کم یا زیاد بودن شاخص «بُعد خانوار» نمیتوان نسبت به ضرورت کاهش یا افزایش جمعیت کشور نتیجهگیری نمود جدول زیر چگونگی روند تغییرات جمعیت و «بُعد خانوار» را طی دوره (1385- 1335) نشان میدهد. 1 ـ جدول تغییرات جمعیت و بُعد خانوار در ایران طی دوره (1385ـ 1335) سال جمعیت کشور متوسط بعد خانوار 1335 18.954.702 4.76 1345 25.788.722 4.99 1355 33.708.744 5.02 1365 49.445.010 5.11 1375 60.055.488 4.84 1385 70.472.846 4.03مأخذ: مرکز آمار ایران (1385) گزیده نتایج سرشماری عمومی نفوس و مسکن ارقام جدول حاکی از این واقعیت است که جمعیت ایران طی 50 سال، از حدود 19 میلیون نفر به حدود 70 میلیون نفر افزایش یافته، در حالی که «بُعد خانوار» در این مدت از 4.76 به 4.03 کاهش یافته است. بنابراین کاهش «بعد خانوار» بهمنزله کاهش جمعیت نیست، نکته قابل تأمل ...
تعاریف و فرمول محاسبه شاخص های سلامت
تعاریف شاخص های سلامت رشد طبیعی جمعیت :(Natural Growth Rate(NGR میزان خام تولد:(Crude Birth Rate(CBR میزان باروری عمومی : (General Fertility Rate(GFR میزانهای باروری اختصاصی سنی : (Age Specific Fertility Rat(ASFR میزان باروری کلی : (Total Fertility Rate(TFR میزان باروری کلی نکاحی: (Total Mirital Fertility (TMFR میزان تجدید نسل ناخالص : (Griss Repeproduction Rate(GRR میزان تجدید نسل خالص : (Net Repeproduction Rate(NRR میزان مرگ خام :(Crude Death Rate(CDR میزانمرگ و میر اختصاصی سنی برای هر دو جنس و کل : (Age Specific Death Rat(ASDR میزان مرگ مرگ مادران به دلیل عوارض بارداری و زایمان میزان مرگ اختصاصی علتی در گروه سنی کمتراز5 سال درصد اشغال تخت در بيمارستان متوسط اقامت بيمار در بيمارستان تخت روز اشغالي ميزان گردش تخت در بيمارستان فاصله چرخش تخت در بيمارستان *رشد طبیعی جمعیت :(Natural Growth Rate(NGR تعریف: عبارت از این است که هرسال به ازای هر هزار نفر جمعیت چند نفر به جمعیت اضافه خواهد شد. *میزان خام تولد: (Crude Birth Rate(CBR تعریف : تعداد کودکان زنده به دنیا آمده به ازای هر هزارنفر جمعیت برآورد شده دروسط سال ؛ دریک سال معین. *میزان باروری عمومی : (General Fertility Rate(GFR تعریف : تعداد موالید زنده درهزار زن گروه سنی 15 تا 49 سال دریک سال معین . *میزانهای باروری اختصاصی سنی : (Age Specific Fertility Rat(ASFR تعریف :تعداد کودکان زنده بدنیا آمده در یکسال بازای هزار زن درهریک از گروههای اختصاصی سنی . *میزان باروری کلی : (Total Fertility Rate(TFR تعریف :نشان دهنده متوسط تعداد کودکان یک زن است به شرط آنکه آن زن بامیزانهای کنونی هریک ازگروههای سنی زنان درسراسر سن باروری خود به زاییدن کودک ادامه دهد . *میزان باروری کلی نکاحی: (Total Mirital Fertility (TMFR تعریف :نشان دهنده متوسط تعداد کودکانی است که یک زن ازدواج کرده بدنیا خواهد آورد به شرط آنکه درسراسر عمر باروری خود به الگوی باروری کنونی ادامه دهد . *میزان تجدید نسل ناخالص : (Griss Repeproduction Rate(GRR تعریف :نشان دهنده تعداد دخترانی است که یک زن ازدواج کرده بدنیا خواهد آورد به شرط آنکه درسراسر عمر باروری خود به الگوی باروری کنونی ادامه دهد . *میزان تجدید نسل خالص : (Net Repeproduction Rate(NRR تعریف :نشان دهنده تعداد دخترانی است که یک دختر تازه زاده شده به فرض ثابت ماندن میزانهای میرایی و باروری اختصاصی سنی ؛ درطول زندکی خود خواهد زایید . *میزان مرگ خام :(Crude Death Rate(CDR تعریف : تعداد مرگهای ناشی از کلیه علل درهزار نفر جمعیت دروسط هرسال ودریک منطقه معین . *میزانمرگ و میر اختصاصی سنی برای هر دو جنس و کل : (Age Specific Death Rat(ASDR تعریف: نشان دهنده تعداد مرگهای اتفاق افتاده در یک گروه سنی خاص به ازای هر هزار نفر جمعیت همان گروه ...
مدل جمعیت ( آمار )
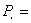
در این مقاله هدف ما،بررسی ساده ترین مدل جمعیت است.یعنی مدل جمعیت یک بعدی تعینی.(یعنی فرض می کنیم فقط یک نوع جمعیت باشد و در آن عوامل تصادفي موثر نیستند.) ما قبل از بیان فرمول مدل جمعیت، مثال زیر را مطرح می کنیم: مثال:متخصصان بر این باورند که زمین های قابل کشت وزرع، حداکثر می تواند غذای 40 میلیارد انسان را تامین کند،در آغاز سال 1990میلادی جمعیت جهان2/5میلیارد نفر تخمين زده شد . اگر جمعیت با میزان رشد ثابت 2% در سال افزایش یابد،در چه زمانی جمعیت به حداكثر میزان ذکر شده خواهد رسید؟ حل: 2/5 = جمعیت اولیه به میلیارد 02/0 = نرخ رشد= r جمعیت در سال میلیارد جمعیت در سال میلیارد جمعیت بعد ازn سال میلیارد حال قرار می دهیم: وn را با لگاریتم گرفتن از طرفین به دست می آوریم : در نتيجه : . یعنی در سال 2093=103+1990 جمعیت به 40 میلیارد نفر می رسد.ما در این مثال، نرخ رشد جمعیت را سال به سال محاسبه کردیم.حال رشد جمعیت را در پايان هر ماه حساب مي کنیم،در مثال بالا نرخ رشد در ماه برابر با : می شود. جمعیت بعد از یک ماه میلیارد جمعیت بعد از دو ماه میلیارد جمعیت در سال 1991= میلیارد جمعیت بعد از n سال = میلیارد جمعیت در سال میلیارد حال اگر جمعیت را روز به روز محاسبه کنیم،نرخ رشد دریک روز برابر با: می شود. جمعیت بعد از یک سال میلیارد جمعیت بعد ازn سال= میلیارد جمعیت در سال 2093 برابر با : میلیارد می شود. حال اگر جمعیت را در هر ساعت محاسبه کنیم،نرخ رشد جمعیت در یک ساعت برابراست با: . جمعیت در سال 2093 برابر است با: اگر جمعیت را در هر ثانیه حساب کنیم،جمعیت در سال 2093 بیش تر می شود و به 799/40میلیارد نفر نزدیک می شود. برای دیدن علت این امر بهتر است به مطلب زیر توجه کنیم: دنباله ی را در نظرمی گیریم.این دنباله را برای مقدار های مختلف n محاسبه می کنیم: قضیه: موجود است و آن را عدد e مي ناميم . ...71828182/2=e حال فرض می کنیم نرخ رشد جمعیتr باشدو جمعیت اولیه را با و جمعیت بعد از tسال را با نشان مي دهیم.اگر جمعیت را سال به سال محاسبه کنیم: و و اگر جمعیت را در سال محاسبه کنیم: یعنی بعد ازt سال درصورتی که در هر سال، جمعیت را محاسبه کنیم،جمعیت به دو متغیر t (زمان) و n (تعداد تقسیمات زمان)بستگی دارد.بنابر این با نشان می دهیم: حال اگر n را بزرگ و بزرگ تر کنیم،یعنی محاسبه ی جمعیت را در مدت زمان های کوتاه تری انجام دهيم ،مدل ما به مدل واقعی جمعیت نزدیک و نزدیک تر می شود.یعنی اگر n را به سمت بی نهایت میل دهیم ،جمعیت در هر لحظه محاسبه می شود.این مدل را مدل پیوسته می نامیم و آن را ...
