فرمول انتگرال
جدول کامل فرمولهای انتگرال
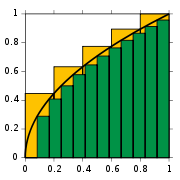
جدول کامل فرمول های انتگرال : Rules for integration of general functions Rational functions Irrational functions Logarithms Exponential functions Trigonometric functions Hyperbolic functions Inverse hyperbolic functions Definite integrals lacking closed-form antiderivatives (if n is an even integer and ) (if is an odd integer and ) (, منبع :ویکی پدیا
انتگرالگیری به روش جز به جز

روش انتگرالگیری جز به جز (Integration by Parts) روشی است که به وسیلهی آن میتوان بسیاری از انتگرالهایی را که با استفاده از فرمولهای رایج قابل حل نیستند، حساب کرد. این روش خصوصا در مواقعی کاربردی است که تابعی که میخواهیم از آن انتگرال بگیریم، حاصلضرب یک تابع جبری و یک تابع مثلثاتی، یا حاصلضرب یک تابع جبری و یک تابع لگاریتمی باشد مانند نمونههای زیر: فرمول روش جز به جز به این صورت است: اگر توابع u و v نسبت به x مشتقپذیر باشند، آنگاه: اثبات: این فرمول با استفاده از قانون «مشتق حاصلضرب» بدست میآید: اگر این فرمول را بازآرایی کنیم داریم: که با انتگرالگیری از آن نسبت به x فرمول انتگرالگیری جز به جز حاصل خواهد شد. اساس کار این فرمول آن است که یک انتگرال داده شده را به انتگرال دیگری تبدیل میکند. اگر u و dv مناسب اختیار شوند، انتگرال جدید ممکن است سادهتر از انتگرال اول باشد. با توجه به اینکه انتخاب u و dv بسیار مهم است، هنگام انتخاب آنها توصیههای زیر میتواند به انتخاب سریعتر و بهتر کمک کند: dv را معمولا باید بخش پیچیدهتر تابع مورد انتگرالگیری که به وسیلهی فرمولهای اساسی انتگرال قابل محاسبه باشد، در نظر گرفت. u را بخشی از تابع مورد انتگرال در نظر میگیرند که مشتقش سادهتر از v است.مثال: حل: و و تذکر: هنگام محاسبه انتگرال به روش جز به جز، u و dv باید به گونهای انتخاب شوند که انتگرال جدید سادهتر از انتگرال اصلی باشد. برای نمونه اگر فرض میکردیم که: و آنگاه: و و روش جز به جز به انتگرال زیر منتهی میشد: و مشاهده میشود که با این کار انتگرال جدید عملا پیچیدهتر از انتگرال اصلی است. ارائهی یک روش ساده برای انتخاب u و v عملا کاری بسیار مشکل است، با وجود این دستورالعملهای کلیای وجود دارند؛ مثلا: «اگر در انتگرال اصلی وجود داشت، نباید dv را گرفت»، زیرا در این صورت توان x پس از اعمال روش جز به جز، بیشتر میشود و انتگرال به دست آمده مشکلتر از قبلی خواهد بود. تذکر: گاهی برای حل یک انتگرال لازم میشود چندین بار از روش جز به جز استفاده کنیم. مثال: که لازم است برای جملهی دوم، همانند مثال قبل، از روش جز به جز استفاده شود. در پایین این صفحه چند مثال دیگر به روش جز به جز حل شده است (زبان انگلیسی)، روی لینک answer کلیک کنید تا جوابها را مشاهده نمایید. در این سایت همچنین میتوانید به صورت آن لاین به جواب انتگرال های مورد نظرتان دست یابید.
خواص انتگرال
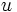
انتگرال، مشتق یک تابع مشتقپذیر برابر است با به علاوه یک ثابت دلخواه. یک ثابت را میتوان از زیر نماد انتگرالگیری بیرون آورد.(توجه شود که عباراتی را که توابعی از متغیر انتگرالگیری اند ، نمیتوان از زیر نماد انتگرالگیری بیرون آورد.) انتگرال مجموع دو تابع برابر مجموع انتگرالهای آنهاست.این مطلب را میتوان به مجموع هر تعداد متناهی از توابع تعمیم داد.
فرمول های مهم انتگرال گیری
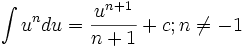
فرمول های انتگرال گیری , , , , در این دستورها یا متغیر مستقل است و یا تابعی مشتقپذیر از متغیر مستقل دیگری است. اگر آنگاه انتگرال نامعین اگر پاد مشتق باشد ، آنگاه به ازای هر مقدار ثابت یک پاد مشتق است.زیرا اگر آنگاه: نکته اگر جوابی برای باشد ، فرمول همه جوابها را به دست میدهد. انتگرال نامعین مجموعه همه پاد مشتقهای یک تابع چون را انتگرال نامعین نسبت به مینامند و با نشان میدهند. هرگاه فرمول همه پادمشتقهای را به دست دهد، آنرا چنین مشخص میکنیم : تابع را انتگرال ده انتگرال و را ثابت انتگرالگیری مینامیم. همچنین نشان میدهد که متغیر انتگرالگیری است.
فرمول انتگرال کوشی
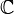
در ریاضیات، فرمول انتگرال کوشی، که به احترام آگوستین لوییز کوشی نامگذاری شدهاست، یک حکم اساسی در آنالیز مختلط است و این حقیقت را بیان میکند که یک (تابع هولومورفیک) (Holomorphic function) تعریف شده بر روی یک قرص، به طور کامل با مقادیرش بر روی حاشیهٔ قرص مشخص میشود. این فرمول همچنین میتواند برای ساده کردن انتگرال همهٔ مشتقات یک تابع تحلیلی به کار رود. فرض کنید U یک زیر مجموعه باز از صفحه مختلط باشد، و f : U → یک تابع هلومورفیک باشد، و قرص D = { z : | z − z0| ≤ r} تماما درون U قرار داشته باشد. و فرض کنید C دایرهای باشد که مرز D را تشکیل میدهد. آنگاه برای هر a در درون D داریم : که انتگرال کانتور (contour integral) در جهت پادساعتگرد گرفته شدهاست. اثبات این حکم از قضیهٔ انتگرال کوشی استفاده میکند و مانند آن قضیه فقط به مشتقپذیر بودن f نیاز دارد. از فرمول میتوان نتیجه گرفت که f در حقیقت باید بینهایت بار به طور پیوسته مشتقپذیر باشد، با برخی این عبارت را فرمول مشتقگیری کوشی مینامند. یک اثبات برای آن، نتیجهٔ فرعی این قضیهاست که توابع هولومورفیک تحلیلیاند. میتوان دایرهٔ C را با هر منحنی تصحیحپذیر بسته در U که هیچ تقاطعی نداشته باشد و پادشاعتگرد جهتدار باشد جایگزین کرد. فرمول برای هر نقطهٔ a از ناحیهٔ احاطه شده توسط این مسیر معتبر باقی میماند. علاوه بر این، فقط در مورد قضیهٔ انتگرال کوشی، کافیست که f در ناحیه باز احاطه شده توسط منحنی، تحلیلی و بر حاشیهٔ آن پیوسته باشد. این فرمولها میتوانند برا اثبات قضیه مانده (residue theorem) استفاده شوند، که یک تعمیم وسیع است. خلاصه اثبات فرمول انتگرال کوشی با استفاده از قضیه انتگرال کوشی میتوان نشان داد که انتگرال بر روی C (یا منحنی بستهٔ تصحیحپذیر) برابر است با انتگرال مشابهی که بر روی یک دایرهٔ بسیار کوچک دور a گرفته شدهاست. مادامی که f(z) پیوستهاست، میتوانیم دایرهای به قدر کافی کوچک انتخاب کنیم که f(z) بر روی آن تقریباً ثابت و برابر f(a) باشد. آنگاه باید انتگرال : را بر روی این دایرهٔ کوچک حساب کنیم. این انتگرال با استفاده از تغییر متغیر قابل حل است. قرار دهید که در آن و . این نشان میدهد که مقدار این انتگرال مستقل از شعاع دایره و برابر 2πi است. کاربرد نمونه تصویر:ComplexResiduesExample.png سطح تابع f(z) = z2 / (z2 + 2z + 2) و نقاط تکین آن، با کانتورهای شرح داده شده در متن. تابع و مسیر |z| = 2 (آن را C بنامید)را در نظر بگیرید. برای بدست آوردن انتگرال f(z) حول مسیر، نیاز به دانستن نقاط تکین f(z) داریم. میتوان f را به صورت زیر نوشت: و قطبها آشکار میشوند. قدر مطلق آنها کمتر از 2 است و بنابراین ...
دانلود كامل ترين مراجع و جداول فرمولهاي انتگرال و.....
دانلود هفت كتاب 1- هندبوک روشهای حل معادلات انتگرالی 2- مرجع جداول انتگرالها و دیگر اطلاعات ریاضی 3- مرجع جداول انتگرالهای نامعین 4- معادلات انتگرالی و دیفرانسیلی(کولینز) 5- معادلات انتگرالی فاینمن(اسمیرنو) 6- انتگرالهای تابعی(کارتیر) 7- تئوری و کابردهای لاپلاس(شیف)Other Printable Tables Most of the table on a single page:PDF | LatexTable of 18 Basic Integrals:PDF | LatexLogic Formulas: PDF | Latex Laplace Transforms:PDF | LatexDifferential Equations Study Guide: PDF | LatexElementary Statistics:PDF | Latex حل انتگرال به صورت آنلاین تاریخچه ی انتگرالها بیش از دو هزار سال پیش ارشمیدس (۲۸۷-۲۱۲ قبل از میلاد) فرمول هایی را برای محاسبه سطح وجه ها ، ناحیه ها و حجم های جامد مثل کره ، مخروط و سهمی یافت . روش انتگرال گیری ارشمیدس استثنایی و فوق العاده بود جبر ، نقش های بنیادی ، کلیات و حتی واحد اعشار را هم نمی دانست . لیبنیز (۱۷۱۶-۱۶۴۶) و نیوتن (۱۷۲۷-۱۶۴۲) حسابان را کشف کردند . عقیده کلیدی آنها این بود که مشتق گیری و انتگرال گیری اثر یکدیگر را خنثی می کنند با استفاده از این ارتباط ها آنها توانستند تعدادی از مسائل مهم در ریاضی ، فیزیک و نجوم را حل کنند. فوریر (۱۸۳۰-۱۷۶۸) در مورد رسانش گرما بوسیله سلسله زمان های مثلثاتی را می خواند تا نقش های بنیادی را نشان دهد .رشته های فوریر و جابجایی انتگرال امروزه در زمینه های مختلفی چون داروسازی و موزیک اجرا می شود . گائوس (۱۸۵۵-۱۷۷۷) اولین جدول انتگرال را نوشت و همراه دیگران سعی در عملی کردن انتگرال در ریاضی و علوم فیزیک کرد . کایوچی (۱۸۵۷-۱۷۸۹) انتگرال را در یک دامنه همبستگی تعریف کرد . ریمان (۱۸۶۶-۱۸۲۶) و لیبیزگو (۱۹۴۱-۱۸۷۵) انتگرال معین را بر اساس یافته های مستدل و منطقی استوار کردند . لیوویل (۱۸۸۲-۱۸۰۹) یک اسکلت محکم برای انتگرال گیری بوجود آورد بوسیله فهمیدن اینکه چه زمانی انتگرال نامعین از نقش های اساسی دوباره در مرحله جدید خود نقش اساسی مرحله بعد هستند . هرمیت (۱۹۰۱-۱۸۲۲) یک شیوه علمی برای انتگرال گیری به صورت عقلی و فکری ( یک روش علمی برای انتگرال گیری سریع ) در دهه ۱۹۴۰ بعد از میلاد استراسکی این روش را همراه لگاریتم توسعه بخشید . در دهه بیستم میلادی قبل از بوجود آمدن کامپیوترها ریاضیدانان تئوری انتگرال گیری و عملی کردن آن روی جداول انتگرال را توسعه داده بودند و پیشرفت هایی حاصل شده بود .در میان این ریاضیدانان کسانی چون واتسون ، تیچمارش ، بارنر ، ملین ، میچر ، گرانبر ، هوفریتر ، اردلی ، لوئین ، لیوک ، مگنوس ، آپل بلت ، ابرتینگر ، گرادشتاین ، اکستون ، سریواستاوا ، پرودنیکف ، برایچیکف و ماریچیف حضور داشتند . در سال ۱۹۶۹ رایسیچ پیشرفت بزرگی در زمینه روش علمی گرفتن ...
