شیب خط
شیب خط

4.2 تابع خط مستقیم (معادله خط) با آگاهی داشتن دو چیز از خط تابع مستقیم ما می توانیم تشخیص بدهیم که خط در کجای دستگاه محور مختصات قرار گرفته است. ما همچنین می توانیم با نگاه کردن به یک خط مستقیم تابع آن را تعیین کنیم. آن دو چیز مهم عبارتند از: (شیب خط) k = ضریب که شیب (جهت) تابع را نشان می دهد.(موقعیت خط) m = نقطه ای است که تابع محور yرا قطع کرده و موقعیت آن را نمایش می دهد. فرمول خط تابع مستقیم ضریب جهت ″ ضریب x″ تعیین کننده ی شیب خط بر روی دستگاه مختصات است. اگر دو تابع هر دو یک عدد را ضریب xداشته باشند، جهت آن دو بر روی دستگاه یکی و موازی خواهد بود. به مثال زیر توجه کنید: با بررسی یک خط (بردار) روی دستگاه محورهای مختصات شما می توانید شیب آن را تشخیص بدهید. امتحان می کنیم: نموداری را در زیر می بینید، ما می خواهیم جهت خط را پیدا کنیم. اگر ما یک پله روی محور xبه سمت راست برویم چه اتفاقی می افتد؟ xبه اندازه یک رقم بزرگترمی شود. ملاحظه می کنید برای هر پله ای که روی محورx به سمت راست می رویم، y سه واحد بزرگترمی شود به عبارت دیگرy در مقابل یک واحد بالا رفتن ارزش x سه واحد بزرگتر می شود. بنابراین نتیجه می گیریم که ضریب x یا ضریب شیب 3 است. روش دیگر تخمین ضریب X این است که با مختصات دو نقطه آشنا باشید: ما نقطه های (1, 0) و (4, 1) را می شناسیم. الان می خواهیم شیب خط ما بین دو خط را حساب کنیم. ما از نقطه (1, 0) شروع می کنیم. ارزش مقداری x از 0 به 1 تغییر میکند, به بیانی دیگر تغییرات برابر با 1+ میباشد. ارزش مقداری y از 1 به 4 تغییر میکند, به بیانی دیگر تغییرات برابر با 3+ میباشد. ضریب شیب جهت :k k = y متغییرات در = + 3 = + 3 x متغیرات در + 1 ضریب شیب جهت 3+ هست که ما در موقع جا بجائی فلش در محور مختصات هم بدست آوردیم. نقطه تقاطع با محورy : حالا ضریب شیب جهت خط را می توانی محاسبه کنی و الان می خواهیم یاد بگیریم که چگونه نقطه تقاطع با محورy را بدست بیاوریم. اگر شما به عکس اول در این بخش را نگاه کنید, می بینید که دو تا از خطها همان جهت ضریب شیب 2 دارند. اما آنها نقطه تقاطع مشترکی ندارند, حالا ما می خواهیم ارزش مقداری موقعیت آنها را حساب کنیم. ...
.:: معادله های خطی ::.
.:: معادله های خطی ::. معادله خط: (Line equation) رابطه ی بین طول (X) و عرض (Y) نقاط واقع بر یک خط را معادله ی آن خط می گویند که به صورت یک تساوی نوشته می شود . مثال: به خط L توجه کنید . نقاط روی این خط قرار دارند .مشاهده می کنیم که طول و عرض این نقاط با هم مساویند . هر نقطه ای که طول و عرض آن مساوی باشد بر خط L قرار می گیرد و هر نقطه ای که روی خط L باشد طول و عرض آن مساوی است. اگر طول هر نقطه را با X و عرض آن را با Y نشان دهیم ، رابطه Y=X را معادله ی خط (L) می نامیم. این تساوی، رابطه ی بین طول و عرض نقاط را مشخص می کند. انواع خط: در هر یک از تصاویر زیر به خط رسم شده توجه کنید .مختصات نقاط داده شده از خط را بیان کنید و معادله ی خط را بنویسید. تصویر 1: حل: نکته: این نوع خط ها موازی محور طول ها هستند و معادله ی آن ها به صورت Y=b نوشته می شود . (b یک عدد ثابت برای همه ی نقاط می باشد.) مانند 1=Y=-2 ، y و ........◦ تصویر2: حل: نکته: این نوع خط ها موازی محور عرض ها هستند و معادله ی آن ها به صورت x=a نوشته می شود. (a یک عدد ثابت برای طول همه ی نقاط می باشد.) مانند 1=X=-2 ، X و ........◦ تصویر3: حل: نکته: این نوع خط از مبدأ مختصات می گذرد و معادله ی آن به صورت Y=mx نوشته می شود. مانند: تصویر 4: حل: نکته: این نوع خط نه موازی محوری است، نه از مبدأ مختصات می گذرد و معادله ی آن به صورت Y=mx+n می با شد. مانند: دانش آموزان عزیز: انواع دیگری از خط را که به نظرتان می رسد در یک صفحه ی مختصات رسم کنید و در مورد معادله خط مربوط به هر کدام تحقیق کنید. صورت استاندارد معادله خط: هر رابطه ی درجه ی اول بین X و Y مانند: 1-Y=2x و 6=3x+Y را معادله ی خط گو یند صورت استاندارد معادله ی خط Y=mx+n می باشد که در آن m و n دو عدد معلوم و مشخص هستند.صورت دیگر معادله ی خط ax+by=c می باشد که در آن c و b و a سه عدد معلوم می باشند که با هم صفر نیستند و آنرا معادله ی خطی یا معادله ی ضمنی می نامند. رسم خطی که معادله ی آن داده شده است: برای رسم یک خط راست به ترتیب زیر عمل می کنیم . الف:مختصات دو نقطه ی دلخواه آن خط را پیدا می کنیم . ب:جای این دو نقطه را درصفحه ی مختصات مشخص می کنیم . ج: این دو نقطه را به هم وصل کرده از دو طرف امتداد می دهیم. مثال:در هر یک از تصاویر زیر معادله ی یک خط داده شده است. نمودار هر یک از خط های داده شده را رسم کنید. تصویر 1: Y=۲x+۵ حل:ابتدا عدد های مختلفی به x می دهیم و عدد های نظیر آن ها را برای y به دست می آوریم. تصویر 2: x+۲y=۴ حل:پیشنهاد:در این معادله ،ابتدا به x عدد صفر را می دهیم و جواب نظیر آنرا برای y بدست می آوریم و سپس بر عکس عمل می کنیم ،به yعدد صفر ...
شیب خط
شیب خط: (gradient of a line) شیب به معنی سرازیری است (مقابل فراز) و در ریاضیات هر چه زاویه ای که خط با محور افقی می سازد بیشتر باشد ، شیب خط بیشتر است و بر عکس هر چه زاویه ای که خط با محور افقی می سازد کمتر باشد ، شیب خط نیز کمتر است. در این پارک کدام سرسره شیب بیشتری دارد ؟ در صفحه ی مختصات زیر کدام خط شیب بیشتری دارد؟ با توجه به خط های بالا y=۳x بیشترین شیب را دارد در مقایسه ی ضریب x مشاهده می کنیم که می باشد یعنی: هر چه ضریبx بیشتر باشدشیب خطبیشتر است و هر چه ضریب x کمتر باشد شیب خط کمتر است به طور کلی می توان گفت: اگر معادله ی خطی به صورت y=ax+b نوشته شود، عدد a که ضریب x می باشد، شیب خط نام دارد . عرض از مبدأ: (y-intercept) فاصله ای که خط از مبدأ گرفته و محور عرض ها را قطع می کند را عرض از مبدأ خط می گویند. به عبارت دیگر: عرض نقطه بر خورد خط با محور y ها را عرض از مبدأ گویند. در صفحه ی مختصات زیر محل بر خورد هر خط با محور عرض ها مشخص شده است. اکنون نقطه های A و B و C را با معادله ی مربوط به هر خط مقایسه کنید. به طور کلی می توان گفت :عدد b در معادله ی y=ax+b را عرض از مبدأ این خط می نامیم .اگر خط از مبدأ مختصات بگذرد عرض از مبدأ آن صفر می شود و معادله ی خط به صورت y=ax در می آید.
آموزش ریاضی سوم - معادله خط
.:: معادله های خطی ::. معادله خط: (Line equation) رابطه ی بین طول (X) و عرض (Y) نقاط واقع بر یک خط را معادله ی آن خط می گویند که به صورت یک تساوی نوشته می شود . مثال: به خط L توجه کنید . نقاط روی این خط قرار دارند .مشاهده می کنیم که طول و عرض این نقاط با هم مساویند . هر نقطه ای که طول و عرض آن مساوی باشد بر خط L قرار می گیرد و هر نقطه ای که روی خط L باشد طول و عرض آن مساوی است. اگر طول هر نقطه را با X و عرض آن را با Y نشان دهیم ، رابطه Y=X را معادله ی خط (L) می نامیم. این تساوی، رابطه ی بین طول و عرض نقاط را مشخص می کند. انواع خط: در هر یک از تصاویر زیر به خط رسم شده توجه کنید .مختصات نقاط داده شده از خط را بیان کنید و معادله ی خط را بنویسید. تصویر 1: حل: نکته: این نوع خط ها موازی محور طول ها هستند و معادله ی آن ها به صورت Y=b نوشته می شود . (b یک عدد ثابت برای همه ی نقاط می باشد.) مانند 1=Y=-2 ، y و ........◦ تصویر2: حل: نکته: این نوع خط ها موازی محور عرض ها هستند و معادله ی آن ها به صورت x=a نوشته می شود. (a یک عدد ثابت برای طول همه ی نقاط می باشد.) مانند 1=X=-2 ، X و ........◦ تصویر3: حل: نکته: این نوع خط از مبدأ مختصات می گذرد و معادله ی آن به صورت Y=mx نوشته می شود. مانند: تصویر 4: حل: نکته: این نوع خط نه موازی محوری است، نه از مبدأ مختصات می گذرد و معادله ی آن به صورت Y=mx+n می با شد. مانند: دانش آموزان عزیز: انواع دیگری از خط را که به نظرتان می رسد در یک صفحه ی مختصات رسم کنید و در مورد معادله خط مربوط به هر کدام تحقیق کنید. صورت استاندارد معادله خط: هر رابطه ی درجه ی اول بین X و Y مانند: 1-Y=2x و 6=3x+Y را معادله ی خط گو یند صورت استاندارد معادله ی خط Y=mx+n می باشد که در آن m و n دو عدد معلوم و مشخص هستند.صورت دیگر معادله ی خط ax+by=c می باشد که در آن c و b و a سه عدد معلوم می باشند که با هم صفر نیستند و آنرا معادله ی خطی یا معادله ی ضمنی می نامند. رسم خطی که معادله ی آن داده شده است: برای رسم یک خط راست به ترتیب زیر عمل می کنیم . الف:مختصات دو نقطه ی دلخواه آن خط را پیدا می کنیم . ب:جای این دو نقطه را درصفحه ی مختصات مشخص می کنیم . ج: این دو نقطه را به هم وصل کرده از دو طرف امتداد می دهیم. مثال:در هر یک از تصاویر زیر معادله ی یک خط داده شده است. نمودار هر یک از خط های داده شده را رسم کنید. تصویر 1: Y=۲x+۵ حل:ابتدا عدد های مختلفی به x می دهیم و عدد های نظیر آن ها را برای y به دست می آوریم. تصویر 2: x+۲y=۴ حل:پیشنهاد:در این معادله ،ابتدا به x عدد صفر را می دهیم و جواب نظیر آنرا برای y بدست می آوریم و سپس بر عکس عمل می کنیم ،به yعدد ...
آموزش مقدماتی رگرسیون با نرم افزار اکسل

آموزش مقدماتی رگرسیون با نرم افزار اکسل نرم افزار اکسل (Excel) یکی از انواع صفحات گسترده ( spreadsheet) میباشد که برای اهداف گوناگون اطلاعاتی از جمله تحلیل آماری به کار میرود . صفحه های گسترده قابلیت تحلیل های بیشرفته آماری را ندارند ولی به دلیل سادگی و محیط زیبا برای کاربر ، محبوبیت دارند . بجز اکسل نرم افزارهای صفحه گسترده دیگری از جمله : Ability Spreadsheet - AppleWorks - Framework - Gnumeric - KDCalc - KSpread - Lotus 1-2-3 - Lotus Improv - Lotus Symphony - Origin - OpenOffice.org Calc - Quantrix Modeler - Quattro Pro - SpreadsheetGear for .NET - The Cruncher و VisiCalc ، برای سیستم های مختلف ساخته شده اند . برای تحلیل های پیشرفته آماری نرم افزار های زیادی وجود دارند که بعضی از آنها عبارتند از : R (زبان برنامه نویسی) SAS - S-Plus - SPSS و ... شروع از – صفر – : در ادامه بصورت مقدماتی انجام یک تحلیل رگرسیون خطی با استفاده از اکسل آموزش داده میشود . شما باید قبل از این آموزش با مفاهیم مقدماتی تحلیل رگرسیون از جمله : متغیر های پاسخ و مستقل ، ضریب تعیین ، ANOVA ، فاصله اطمینان ، نمودار نرمال و... آشنا باشید . در این آموزش از نسخه 2002 برنامه اکسل استفاده میکنیم ، که ظاهری شبیه به شکل زیر دارد : (با کلیک روی تصاویر موجود میتوانید آنها را بزرگتر ببینید ) داده ها را در ستون A و B به ترتیب برای متغیر وابسته (Y) و رگرسور (X) وارد میکنیم . برای مثال نمونه 20 تایی زیر وارد شده است برای انجام تحلیل های آماری نیاز به یک بسته اضافی (Add-in) داریم ، که بصورت زیر نصب میشود :از منوی Tools گزینه Add-Ins… را انتخاب کنید : در پنجره باز شده گزینه اول یعنی Analysis ToolPack را علامت بزنید و OK را انتخاب کنید . اگر گزینه اول از پیش دارای علامت تیک هست بدون انجام کاری OK را انتخاب کنید . در این مرحله ممکن است پیام زیر ظاهر شود که باید CD برنامه را در درایو قرار دهید و دکمه Yes را بزنید تا مراحل نصب تمام شود . بعد از این کار از منو Tools گزینه Data Analysis… را انتخاب کنید . از پنجره باز شده Regression را انتخاب کنید و کلید OK را بزنید . در این پنجره 4 قسمت وجود دارد : ورودی : روی فضای خالی روبروی عبارت Input Y Range : کلیک کنید و سلول های ستون A را از 1 تا 20 انتخاب نمایید یا مستقیماً عبارت زیرر را بنویسید : A$1:$A$20$ . (این کار محدوده متغیر وابسته را مشخص میکند . داده ها میتواند هر جای دیگر بصورت ستونی قرار گیرد و تنها عبارت بالا تغییر خواهد کرد . ) این کار را برای متغیر رگرسور نیز در فضای روبروی عبارت Input X Range تکرار کنید یا عبارت $B$1:$B$20 را تایپ کنید .اگر برای ستون داده ها در ردیف اول اسمی نوشته باشید باید گزینه Labels را علامت بزنید ، که در این مثال لازم نیست .گزینه مقابل هم برای رگرسیون ...
انیمیشن مفهوم شیب خط پایه سوم
شیب خط یعنی نسبتتفاضل عرض های دو نقطه (روی خط) به تفاضل طول های همان دو نقطه در تصویر زیر رابطه بین شیب خط و زاویه بین خط و محور طول ها را به خوبی می توان مشاهده نمود
فلش های آموزشی (شیب و معادله خط)
صفحه فلش های آموزشی دانلودهادانلود خط 1 دانلود خط 2 دانلود خط 3 دانلود خط 4 دانلود خط 5
معادله ی خط
معادله خط: (Line equation) رابطه ی بین طول (X) و عرض (Y) نقاط واقع بر یک خط را معادله ی آن خط می گویند که به صورت یک تساوی نوشته می شود . مثال:به خط L توجه کنید . نقاط روی این خط قرار دارند .مشاهده می کنیم که طول و عرض این نقاط با هم مساویند . هر نقطه ای که طول و عرض آن مساوی باشد بر خط L قرار می گیرد و هر نقطه ای که روی خط L باشد طول و عرض آن مساوی است. اگر طول هر نقطه را با X و عرض آن را با Y نشان دهیم ، رابطه Y=X را معادله ی خط (L) می نامیم. این تساوی، رابطه ی بین طول و عرض نقاط را مشخص می کند. انواع خط: در هر یک از تصاویر زیر به خط رسم شده توجه کنید .مختصات نقاط داده شده از خط را بیان کنید و معادله ی خط را بنویسید. تصویر 1: حل: نکته: این نوع خط ها موازی محور طول ها هستند و معادله ی آن ها به صورت Y=b نوشته می شود . (b یک عدد ثابت برای همه ی نقاط می باشد.) مانند 1=Y=-2 ، y و ........◦ تصویر2: حل: نکته: این نوع خط ها موازی محور عرض ها هستند و معادله ی آن ها به صورت x=a نوشته می شود. (a یک عدد ثابت برای طول همه ی نقاط می باشد.) مانند 1=X=-2 ، X و ........◦ تصویر3: حل: نکته: این نوع خط از مبدأ مختصات می گذرد و معادله ی آن به صورت Y=mx نوشته می شود. مانند: تصویر 4: حل: نکته: این نوع خط نه موازی محوری است، نه از مبدأ مختصات می گذرد و معادله ی آن به صورت Y=mx+n می با شد. مانند: دانش آموزان عزیز:انواع دیگری از خط را که به نظرتان می رسد در یک صفحه ی مختصات رسم کنید و در مورد معادله خط مربوط به هر کدام تحقیق کنید. صورت استاندارد معادله خط: هر رابطه ی درجه ی اول بین X و Y مانند: 1-Y=2x و 6=3x+Y را معادله ی خط گو یند صورت استاندارد معادله ی خط Y=mx+n می باشد که در آن m و n دو عدد معلوم و مشخص هستند.صورت دیگر معادله ی خط ax+by=c می باشد که در آن c و b و a سه عدد معلوم می باشند که با هم صفر نیستند و آنرا معادله ی خطی یا معادله ی ضمنی می نامند. رسم خطی که معادله ی آن داده شده است: برای رسم یک خط راست به ترتیب زیر عمل می کنیم . الف:مختصات دو نقطه ی دلخواه آن خط را پیدا می کنیم . ب:جای این دو نقطه را درصفحه ی مختصات مشخص می کنیم . ج: این دو نقطه را به هم وصل کرده از دو طرف امتداد می دهیم. مثال:در هر یک از تصاویر زیر معادله ی یک خط داده شده است. نمودار هر یک از خط های داده شده را رسم کنید. تصویر 1: Y=۲x+۵ حل:ابتدا عدد های مختلفی به x می دهیم و عدد های نظیر آن ها را برای y به دست می آوریم. تصویر 2: x+۲y=۴ حل:پیشنهاد:در این معادله ،ابتدا به x عدد صفر را می دهیم و جواب نظیر آنرا برای y بدست می آوریم و سپس بر عکس عمل می کنیم ،به yعدد صفر می دهیم و جواب ...
انیمیشن مفهوم شیب خط پایه نهم
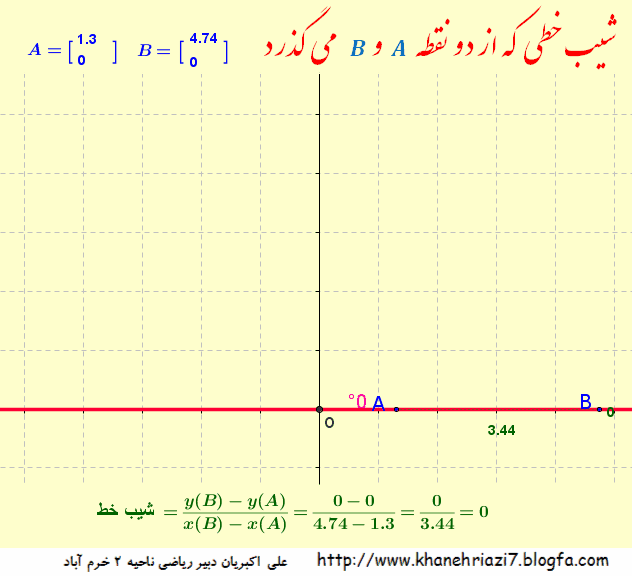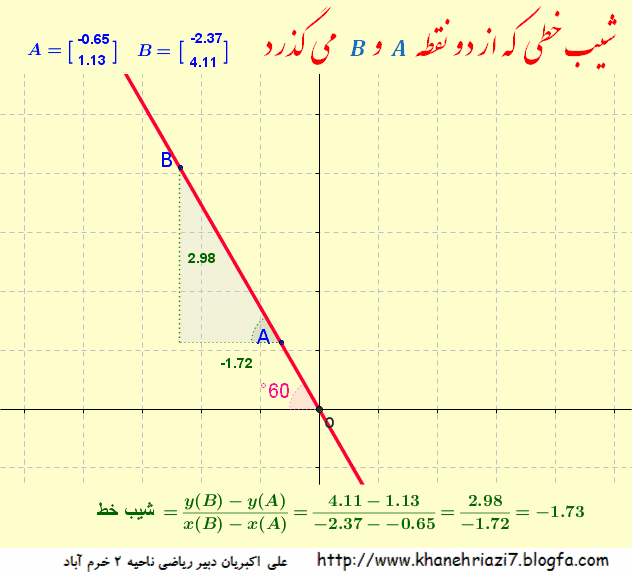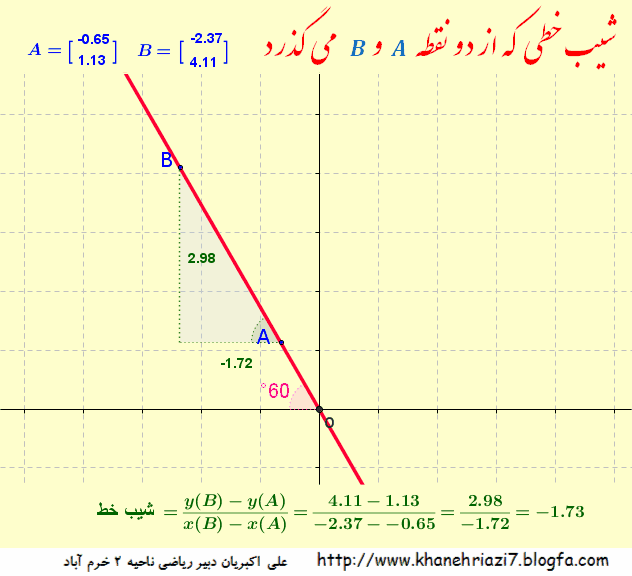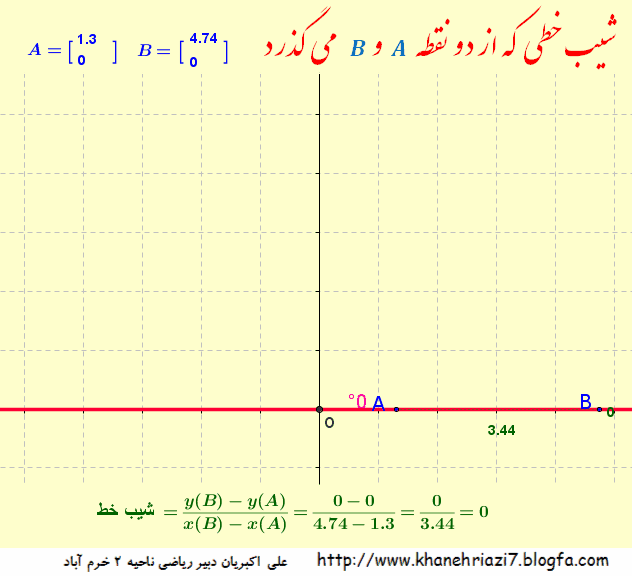
شیب خط یعنی نسبتتفاضل عرض های دو نقطه (روی خط) به تفاضل طول های همان دو نقطه در تصویر زیر رابطه بین شیب خط و زاویه بین خط و محور طول ها را به خوبی می توان مشاهده نمود
