سوالات لگاریتم
نمونه سوال لگاریتم
دانلود
نمونه سوالات لگاریتم تستی
دانلود نمونه سوالات لگاریتمی : دانلود تهیه و تنظیم توسط : علیرضا کاوسی
سوالات کنکور برای لگاریتم و توابع درجه 2
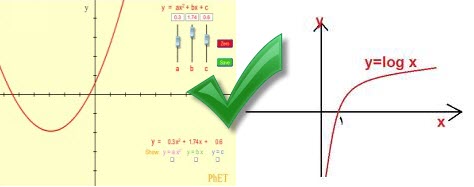
پست حاضر حاوی سوالات کنکور پیرامون مبحث درسی لگاریتم و تابع درجه دو همراه با پاسخ میباشد.دانلود از سایت گروه ریاضی مراغهتابع درجه دولگاریتم
نکات آموزشی تابع نمایی ولگاریتم
بسمه تعالي نكات كمك آموزشي تابع نمايي وتابع لگاريتم رياضي2 تابع نمايي: به توابعي باضابطه ي f(x)=ax كه درآنa ،عددي مثبت ومخالف صفر است ،تابع نمايي گوييم (به وضوح ميتوان ديد تابع نمايي كه تابعي همواره مثبت است . نمودار تابع y=ax باشرط 1 <a به صورت روبه رو است : ونمودار تابع y=ax با شرط 1 > a > 0 به صورت مقابل مي باشد. نكته :صعود ونزول در توابع نمايي 1) در تابع y=ax با شرط 1 < a ،با افزايش x، مقدار تابع هم زياد مي شود مثال - براي تابع x 2 = y داريم : 2) در تابع y=ax با شرط 1 >a > 0 با افزايش مقدار x ، مقدار تابع كم مي شود مثال – براي تابع داريم: 15 <17 دامنه وبرد توابع نمايي: درتابع نمايي f(x)=ax ، x هرمقدار حقيقي مي تواند باشدوبا توجه به نمودار به وضوح مقدار تابع هر عدد حقيقي مثبت مي تواند باشد پس دامنه وبرد : و به طور مثال برد تابع 1 y= 2x+1+ خواهد شد: 1<y 1 < 1+ x+1 2 0< x+1 2 0< x 2 نامساوي ميانگين هندسي وحسابي : دونامساوي زير كه به نامساوي ميانگين حسابي وهندسي مشهور هستند در محاسبه برد توابع نمايي كاربرد زيادي دارند . 2 ≤a + b 0≤bو0≤a (1 2- ≥ a+b 0≥b و 0 ≥ a (2 مثال: برد تابع –x+3 2 + x+1 2 = f(x) راحساب كنيد. ( و8]= 2≤ -x+32 + x+1 2 تعريف لگاريتم : تابع نمايي xa =y يك تابع يك به يك است بنابراين وارون پذير است .وارون اين تابع ، تابع لگاريتم نام دارد وبه صورت مي باشد. نكته: چون لگاريتم يك تابع يك به يك است داريم: قانون تغيير مبنا: يكي از قوانين مفيد لگاريتم قانون تغيير مبنا ست . نتيجه1: درحالت خاص 10=c به تساوي مي رسيم. نتيجه2: با استفاده از نتيجه 1 داريم: نتيجه3: با تركيب قانون ونتيجه 1 به دست مي آوريم: مثال: مقدار را حساب كنيد. نكته: ...
لگاریتم
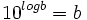
مقدمه در جبر عموما لگاریتم معمولی یا لگاریتم در پایه 10 عدد b را توانی تعریف میکنند که 10 باید به آن برسد تا b بدست آید: . فرض کنیم چنین عددی موجود بوده و از لگاریتمها برای سادهکردن ضرب اعدادی که ارقام اعشاری زیادی دارند استفاده میکنیم. تعریف تابع لگاریتم طبیعی بصورت زیر نمایش داده میشود: به ازای هر x بزرگتر از 1 ، این انتگرال مساحت ناحیهای را نشان میدهد که از بالا به خم از پایین به محور t از طرف چپ به خط t=1 ، و از طرف راست به خط t=x محدود است. تاریخچه در اواخر قرن شانزدهم یک بارون اسکاتلندی به نام جان نپر (1550-1617) ابزاری بنام لگاریتم ابداع کرد که با تبدیل ضرب به جمع کار محاسبه را ساده میکند؛ یعنی داریم: لگاریتم x + لگاریتم a = لگاریتم ax برای ضرب دو عدد مثبت x,a از یک جدول ، لگاریتمهای x,a را پیدا میکنیم، سپس این لگاریتمها را بهم میافزائیم مجموع حاصل را در داخل جدول مییابیم، و بالاخره حاصلضرب مطلوب ax را از حاشیه جدول میخوانیم. مسلما در دست داشتن جدول کلید کار بود، به همین سبب نپر در دو دهه آخر زندگیاش را صرف تهیه جدولی کرد که هیچگاه نتوانست آن را تمام کند. و این در حالی بود که تیکو براهه ستاره شناس ، مشتاقانه در انتظار این جدول بود تا میتواند محاسبات خودش را تسریع بخشد مشتق تابع لگاریتم طبیعی چون تابع با انتگرال ذکر شده در قسمت تعریف ، تعریف میشود، فورا از نخستین قضیه اساسی حساب دیفرانسیل و انتگرال نتیجه میشود که مشتق تابع برابر خواهد بود. بنابراین اگر u تابع مشتقپذیری از x باشد، آنگاه از قاعده زنجیری داریم: فرمول کلیتر زیر بدست میآید: مشتقگیری لگاریتمی گاهی یک تابع با معادلهای پیچیده داده شده با گرفتن لگاریتم از طرفین آن پیش از مشتقگیری میتوان مشتقش را سریعتر حساب کرد. خواص قلمرو: مجموعه تمام اعداد حقیقی مثبت ، x>0 برد: مجموعه تمام اعداد حقیقی این تابع بر قلمرو خود پیوسته و صعودی است هر گاه آنگاه . این تابع یک تابع یکبهیک از قلمرو خود به بردش است، بنابراین دارای معکوس است. حاصلضرب ، خارج قسمت و توان: هر گاه x,a دو عدد مثبت باشند. آنگاه:معکوس تابع لگاریتم چون یکبهیک و مشتقپذیر است، دارای معکوس مشتقپذیر میباشد نمودار منعکس نمودار تابع نسبت به خط y=x است. این نمودار تابع نیز میباشد. تابع به ازای هر عدد حقیقی x مساوی میباشد. تابع حاصل تابع مشتق پذیری از x است که به ازای هر x حقیقی تعریف شده است و بعنوان تابع نمایی از آن یاد میشود که e را پایه و x نما خوانده میشود. همچنین توجه میکنیم که حد تابع نمایی زمانی که x بسمت بینهایت میل میکند برابر بینهایت است و زمانی ...
اعلام نفرات برتر المپیاد ریاضیات (مبحث لگاریتم)
اسامی دانش آموزان برتر المپیاد ریاضیات شهرستان دلفان دانش آموزان گرامی با هماهنگی با مدیر دبیرستان جهت دریافت تشویقی و جایزه به کارشناسی گروهها (گروه ریاضیات متوسطه) مراجعه نمایند. نام و نام خانوادگی دبیرستان سپهر دادستان زکریای رازی حسین جوادی زکریای رازی علی کاوه ای زکریای رازی الهه قربانی رضوان برخوردار ندا سهرابی رضوان برخوردار رسول محمدیانی زکریای رازی مریم جمشیدی معراج اسماء مرادی صدر ۲ کوثر صالحی صدر ۱ شیوا رضایی صدر ۲برای دیدن سوالات مسابقه بحث لگاریتم اینجا را کلیک نمایید.
