زوایای مثلثاتی
توابع مثلثاتی
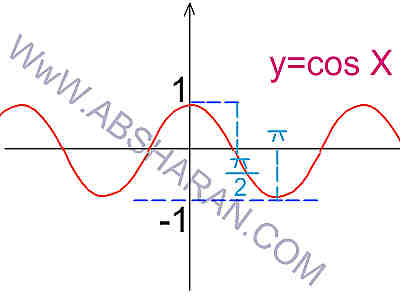
تابع مثلثاتی Cos نیز یکی از توابع مهم مثلثاتی است.همانطور که از نمودارد تابع مثلثاتی Cos پیداست,این تابع یک تابع زوج است (نسبت به محور Y قرینه است).دامنه ی تابع مثلثاتی Cos مجوعه ی اعداد حقیقی و برد این تابع مثلثاتی اعداد بین 1 و 1- می باشند.یعنی مقدار از 1 بیشتر و از 1- کمتر نمی شود.نمودار تابع Cos بصورت زیر است: با توجه به نمودار تابع مثلثاتی Cos این تابع نیز یک به یک نمی باشد.از آنجاییکه تابع Cos یک تابع زوج است پس رابطه ی زیر برقرار می باشد: آموزش مثلثات,تابع مثلثاتی سینوس Sin یکی از توابع پرکاربرد مثلثاتی است.همانطور که از نمودار تابع مثلثاتی سینوس پیداست,این تابع یک تابع فرد است (نسبت به مبداء مختصات قرینه است).دامنه ی تابع مثلثاتی سینوس sin مجوعه ی اعداد حقیقی و برد این تابع مثلثاتی اعداد بین 1 و 1- می باشند.یعنی مقدار سینوس از 1 بیشتر و از 1- کمتر نمی شود.نمودار تابع Sin سینوس بصورت زیر است: با توجه به نمودار تابع مثلثاتی سینوس Sin این تابع یک به یک نیز نمی باشد.از آنجاییکه تابع سینوس یک تابع فرد است پس رابطه ی زیر برقرار می باشد: Y=Sin(-X)=-SinX آموزش مثلثاتدر ابتدای آموزش مثلثات به بررسی دایره ی مثلثاتی می پردازیم,دایره ی مثلثاتی شما را در یافتن مقادیر زاویه ها در مثلثات یاری می کند.: هر دایره دارای یک مبداء بوده که شروع حرکت متحرک از آن جا آغاز می گردد,دارای 4 ناحیه می باشد,دارای جهت اصلی خلاف عقربه های ساعت (جهت مثبت) می باشد.دارای 4 محور است که محور سینوس Sin و تانژانت tg موازی هم و محور Cos و کتانژانت Cotg در دایره ی مثلثاتی موازی هم هستند. تغییرات sin و cos بین 1 و 1- و تغییرات تانژانت tg و cotg از تا است. روش محاسبه ی نسبت های مثلثاتی: برای محاسبه ی sin و cos یک زاویه انتهای کمان را بر محور Sin و یا cos عمود می کنیم,ولی برای محاسبه ی tg و یا cotg یک زاویه انتهای کمان را امتداد داده تا محور tg و یا cotg را قطع کند. اگر x زاویه ای در ناحیه ی اول باشد,در ناحیه ی اول تمام نسبت های مثلثاتی مثبت است. اگر x در ناحیه ی دوم باشد فقط سینوس sin مثبت است. اگر x در ناحیه ی سوم باشد در ناحیه ی سوم سینوس sin و cos منفی و تانژانت tg و کتانژانت cotg مثبت است. اگر x در ناحیه ی چهارم باشد,در ناحیه ی چهارم فقط cos مثبت است. ده رابطه ی مهم مثلثاتی: ================================================================================================ نسبت های مثلثاتی کمان 2x : ============================================================================= نسبت های مثلثاتی زوایای 3x : ================================================================================================= نکته: ==================================================================================================== چند نسبت دیگر: ================================================================================================== فرمول ...
جدول نسبتهای مثلثاتی برای زوایای 0 تا 90 درجه
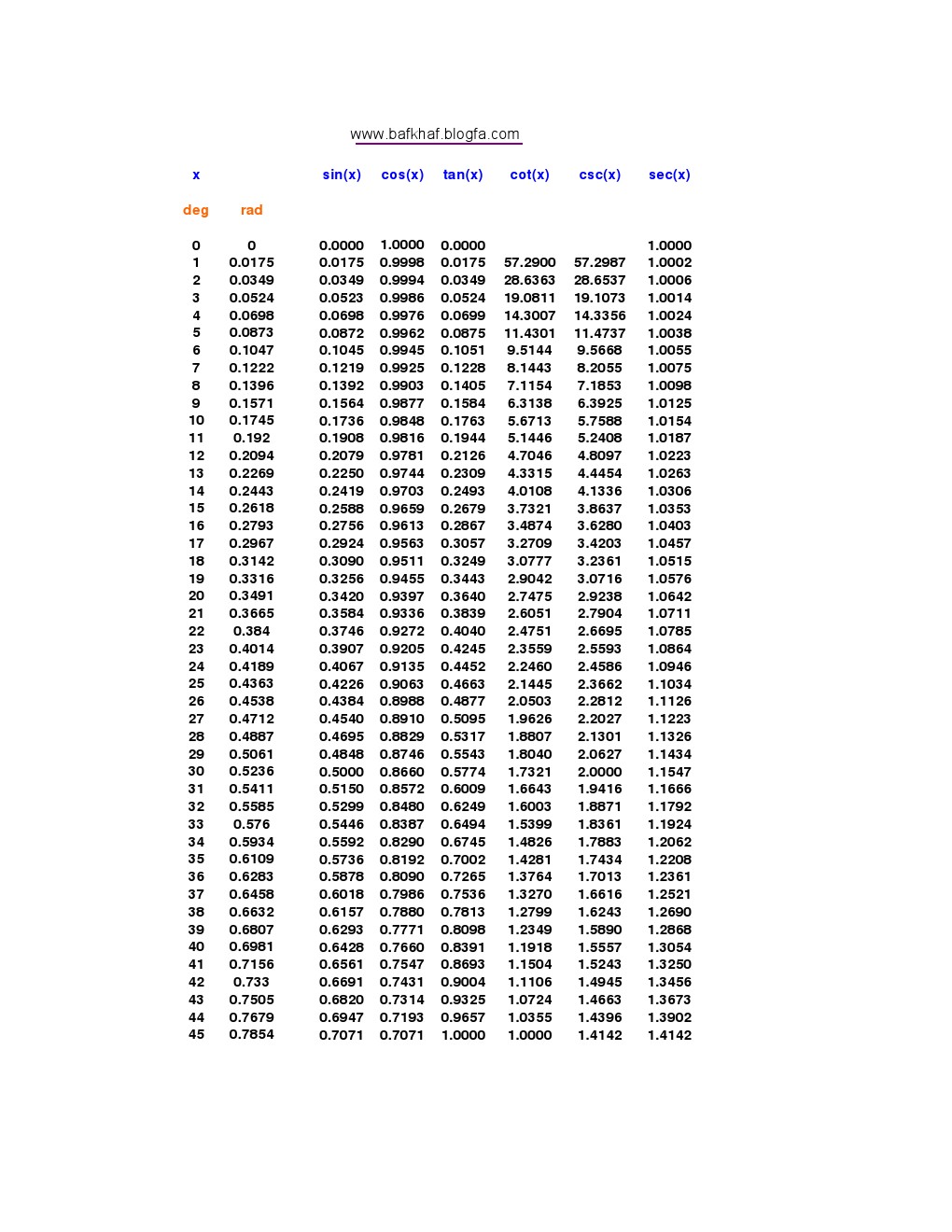
این عکسها قابلیت زوم بالایی دارند تا در موبایل و کامپیوتر استفاده شوند. همچنین میتوان از آنها پرینت گرفت.
مثلث
مثلث ار اساسی ترین اشکال در هندسه میباشد.یک مثلث دارای سه راس است که سه ضلع این رئوس را به هم وصل میکند.در هندسه اقلیدسی این اضلاع خطوطی مستقیم هستند. ولی در هندسه کروی این اضلاع کمان هایی از دایره عظیمه میباشند.این دو نوع مثلث را میتوانید در شکلهای روبرو مشاهده نمایید. انواع مثلث مثلث متساوی الاضلاع: مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای داخلی این مثلث نیز با هم برابرند. مثلث متساوی الساقین: مثلثی است که دارای دو ضلع با طولهای مساوی است و دو زاویه داخلی برابر دارد. البته مثلث میتواند دارای سه ضلع با طولهای مختلف و زوایای غیر مساوی باشد. مثلث قائم الزاویه: مثلثی را گویند که یکی از زوایای آن 90درجه باشد.نسبت های مثلثاتی مانند sin و cos ،بر روی مثلث قائم الزاویه تعریف میشوند. مثلث منفرجه: مثلثی را گویند که یکی از زوایای داخلی آن بیشتر از 90 درجه باشد. مثلث حاده : مثلثی را گویند که تمام زوایای داخلی آن کمتر از 90 درجه باشد. 300 سال قبل از میلاد اقلیدس ،اصول اولیه درباره مثلث را ارائه داد.به عنوان مثال یکی از اصول مهم در مورد مثلث این است که مجموع زوایای داخلی یک مثلث برابر 180 درجه است. بر اساس این اصل میتوان با معلوم بودن دو زاویه از مثلث اندازه زاویه سوم را بدست آورد. یکی از مهمترین قضایای موجود در مثلثات قضیه فیثاغورس میباشد.در این قضیه رابطه بین وتر و اضلاع قائم یک مثلث قائم الزاویه بیان میشود. محاسبه مساحت مثلث برای محاسبه مساحت یک مثلث روشهای مختلفی وجود داردو در ادامه به توضیح این روشها میپردازیم: روش هندسی برای محاسبه مساحت یک مثلث باید طول ارتفاع مثلث و نیز طول قاعده(ضلعی که ارتفاع بر آن عمود است) آن را داشته باشیم.آنگاه میتوانیم از فرمول زیر استفاده کنیم: در این فرمول b طول قاعده و h طول ارتفاع مثلث میباشد. در شکل زیر نحوه بدست آمدن این فرمول بیان شده است: تبدیل مثلث به یک متوازی الاضلاع که دو برابر مثلث مساحت دارد وسپس تبدیل متوازی الضلاع به یک مستطیل برای پیدا کردن مساحت مثلث (قسمت سبز) ابتدا یک کپی از مثلث (قسمت آبی) را برداشته و آن را 180 درجه میچرخانیم و به مثلث اولیه متصل میکنیم تا یک متوازی الاضلاع بدست آید. با بریدن قسمتی از متوازی الاضلاع و متصل کردن آن به ضلع دیگر آن(همانند شکل) یک مستطیل ایجاد میشود. چون مساحت مستطیل برابر bh است .پس مساحت مثلث اولیه، نصف این مساحت خواهد بود. روش برداری محاسبه مساحت متوازی الاضلاع با استفادهاز ضرب خارجی دو بردار مساحت یک متوازی الاضلاع را میتوان با استفاده از بردارها محاسبه کرد.اگر AB,AC را مطابق شکل فرض کنیم آنگاه مساحت ABCD برابر |AB × AC| ...
نسبت های مثلثاتی
مطالعه روی زوایا و روابط موجود میان زوایای اشکال مسطح و سه بعدی مثلثات نامیده میشود.تابع مثلثاتی از قبیل سینوس و کسینوس توابعی هستند که بوسیله روابط هندسی تعریف میشوند.تاریخچه اولین کسانی که از مثلثات استفاده میکردند یونانیان بودند.در یونان قدیم از مثلثات برای تعیین طول مدت روز یا طول سال (با مشخص کردن موقعیت ستارگان در آسمان)استفاده میشد.بعدها ریاضیدانان و منجمان هندی نیز پیشرفتهایی در مثلثات بدست آوردند ولی پیشرفت این علم مدیون دانشمندان مسلمان است .مسلمانان اصلیترین نقش را در پیشرفت این علم ایفا کردند و سپس این اندوختهها را در قرون وسطی به اروپاییان منتقل کردند. اروپاییان نیز دانش فراوان مسلمانان در مثلثات استفاده کردند و این علم را توسعه داده و به شکل امروزی در آوردند.کاربردها علم مثلثات در نجوم کاربرد فراوانی دارد و ازآن برای اندازهگیری فواصل بین ستارگان استفاده میشود. همچنین در طراحی سیستمهای ماهواره ای از مثلثات استفاده فراوانی میشود.در دریانوردی نیز از مثلثات برای تشخیص جهتهای جغرافیایی کمک گرفته میشود.امروزه از مثلثات در شاخه های مختلف فیزیک ماننداپتیک ، اکوستیک ، در تحلیل بازارهای مالی، الکترونیک ، معماری ، اقیانوس شناسی ، مکانیک ، بلور شناسی ، ژئودزی ، عمران و اقتصاد استفاده فراوانی میشوددایره مثلثاتیدر ریاضیات دایره مثلثاتی دایرهای به شعاع واحد است. x و y دو مختصه روی این دایره هستند که بنا به تعریف دایره:x2 + y2 = 1نقطه (x, y) روی این دایره با (۰, ۰) زاویهای میسازد که از روابط زیر بدست میآید:دایره مثلثاتی با نمایش زاویه t در نقطه (x, y)بنابر این خواهیم داشت:و از آنجا که توابع سینوس و کسینوس دورهای (پریودیک) هستند:که در آن k عددی صحیح است. سایر توابع مثلثاتی نظیر تانژانت و کتانژانت و سکانت و کسکانت را میتوان به همین ترتیب بدست آورد.فرمولهای مهم مثلثاتفرمول های مهم مثلثات برای تبدیل و محاسبهـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــ(فرمول طلایی)ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــ(تبدیل ضرب به جمع)ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ...
مثلث
انواع مثلث مثلث متساوی الاضلاع: مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای داخلی این مثلث نیز با هم برابرند. مثلث متساوی الساقین: مثلثی است که دارای دو ضلع با طولهای مساوی استو دو زاویه داخلی برابر دارد. البته مثلث میتواند دارای سه ضلع با طولهای مختلف و زوایای غیر مساوی باشد. مثلث قائم الزاویه: مثلثی را گویند که یکی از زوایای آن 90درجه باشد.نسبت های مثلثاتی مانند sin و cos ،بر روی مثلث قائم الزاویه تعریف میشوند. مثلث منفرجه: مثلثی را گویند که یکی از زوایای داخلی آن بیشتر از 90 درجه باشد. مثلث حاده : مثلثی را گویند که تمام زوایای داخلی آن کمتر از 90 درجه باشد. 300 سال قبل از میلاد اقلیدس ،اصول اولیه درباره مثلث را ارائه داد.به عنوان مثال یکی از اصول مهم در مورد مثلث این است که مجموع زوایای داخلی یک مثلث برابر 180 درجه است. بر اساس این اصل میتوان با معلوم بودن دو زاویه از مثلث اندازه زاویه سوم را بدست آورد. یکی از مهمترین قضایای موجود در مثلثات قضیه فیثاغورث میباشد.در این قضیه رابطه بین وتر و اضلاع قائم یک مثلث قائم الزاویه بیان میشود.
روش محاسبه سطح مثلث و اشکال هندسی
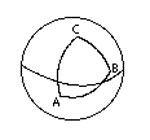
مثلث ار اساسی ترین اشکال در هندسه میباشد.یک مثلث دارای سه راس است که سه ضلع این رئوس را به هم وصل میکند.در هندسه اقلیدسی این اضلاع خطوطی مستقیم هستند. ولی در هندسه کروی این اضلاع کمان هایی از دایره عظیمه میباشند.این دو نوع مثلث را میتوانید در شکلهای روبرو مشاهده نمایید. انواع مثلثمثلث متساوی الاضلاع: مثلثی است که دارای سه ضلع با طولهای مساوی است و زوایای داخلی این مثلث نیز با هم برابرند.مثلث متساوی الساقین: مثلثی است که دارای دو ضلع با طولهای مساوی استو دو زاویه داخلی برابر دارد.البته مثلث میتواند دارای سه ضلع با طولهای مختلف و زوایای غیر مساوی باشد.مثلث قائم الزاویه: مثلثی را گویند که یکی از زوایای آن 90درجه باشد.نسبت های مثلثاتی مانند sin و cos ،بر روی مثلث قائم الزاویه تعریف میشوند.مثلث منفرجه: مثلثی را گویند که یکی از زوایای داخلی آن بیشتر از 90 درجه باشد.مثلث حاده : مثلثی را گویند که تمام زوایای داخلی آن کمتر از 90 درجه باشد.300 سال قبل از میلاد اقلیدس ،اصول اولیه درباره مثلث را ارائه داد.به عنوان مثال یکی از اصول مهم در مورد مثلث این است که مجموع زوایای داخلی یک مثلث برابر 180 درجه است. بر اساس این اصل میتوان با معلوم بودن دو زاویه از مثلث اندازه زاویه سوم را بدست آورد.یکی از مهمترین قضایای موجود در مثلثات قضیه فیثاغورث میباشد.در این قضیه رابطه بین وتر و اضلاع قائم یک مثلث قائم الزاویه بیان میشود. محاسبه مساحت مثلثبرای محاسبه مساحت یک مثلث روشهای مختلفی وجود داردو در ادامه به توضیح این روشها میپردازیم روش هندسیبرای محاسبه مساحت یک مثلث باید طول ارتفاع مثلث و نیز طول قاعده(ضلعی که ارتفاع بر آن عمود است) آن را داشته باشیم.آنگاه میتوانیم از فرمول زیر استفاده کنیم: در این فرمول b طول قاعده و h طول ارتفاع مثلث میباشد. در شکل زیر نحوه بدست آمدن این فرمول بیان شده است: تبدیل مثلث به یک متوازی الاضلاع که دو برابر مثلث مساحت دارد وسپس تبدیل متوازی الضلاع به یک مستطیلبرای پیدا کردن مساحت مثلث (قسمت سبز) ابتدا یک کپی از مثلث (قسمت آبی) را برداشته و آن را 180 درجه میچرخانیم و به مثلث اولیه متصل میکنیم تا یک متوازی الاضلاع بدست آید. با بریدن قسمتی از متوازی الاضلاع و متصل کردن آن به ضلع دیگر آن(همانند شکل) یک مستطیل ایجاد میشود. چون مساحت مستطیل برابر bh است .پس مساحت مثلث اولیه، نصف این مساحت خواهد بود.روش برداری محاسبه مساحت متوازی الاضلاع با استفادهاز ضرب خارجی دو بردارمساحت یک متوازی الاضلاع را میتوان با استفاده از بردارها محاسبه کرد.اگر AB,AC را مطابق شکل فرض کنیم آنگاه مساحت ABCD برابر |AB × AC| خواهد بود.این ...
