رگرسیون چند متغیره در spss
آموزش رگرسیون چند متغیره در spss
کاربرد يک متغير براى پيشبينى متغير ديگر را رگرسيون مىگويند. رگرسيون با کاربرد يک متغير دانسته و مشخص، مقادير متغير غيرمشخص ديگرى را پيشبينى مىکند. رگرسيون بصورت دو متغيره و چند متغيره محاسبه مىشود. در رگرسيون دو متغيره، يک متغير مستقل و يک متغير تابع وجود دارد؛ ولى در رگرسيون چند متغيره يک متغير تابع و چند متغير مستقل وجود دارد؛ مثلاً در محاسبهٔ تأثير دو متغير تحصيلات و تجربه شغلى در درآمد، درآمد متغير تابع است و تحصيلات و تجربه شغلى دو متغير مستقل هستند. در ادامه یک فایل آموزش تصویری رگرسیون چند متغیره در نرم افزار spss قرار داده شده است. دانلود فایلبرای انجام تحلیل پروژه اماری خود توسط نرم افزار spssدر کمتر از 3 روز و یا در صورت اضطراری کمتر،با شماره زیر تماس بگیرید. 09371559986
آموزش رگرسیون چند متغیره در spss
کاربرد يک متغير براى پيشبينى متغير ديگر را رگرسيون مىگويند. رگرسيون با کاربرد يک متغير دانسته و مشخص، مقادير متغير غيرمشخص ديگرى را پيشبينى مىکند. رگرسيون بصورت دو متغيره و چند متغيره محاسبه مىشود. در رگرسيون دو متغيره، يک متغير مستقل و يک متغير تابع وجود دارد؛ ولى در رگرسيون چند متغيره يک متغير تابع و چند متغير مستقل وجود دارد؛ مثلاً در محاسبهٔ تأثير دو متغير تحصيلات و تجربه شغلى در درآمد، درآمد متغير تابع است و تحصيلات و تجربه شغلى دو متغير مستقل هستند. در ادامه یک فایل آموزش تصویری رگرسیون چند متغیره در نرم افزار spss قرار داده شده است. دانلود فایل
رگرسیون چند متغیره در اکسل
برای انجام رگرسیون چند متغیره در اکسل شما ابتدا باید ابزار تحلیل داده ها را در اکسل نصب کرده باشید.(برای آموزش نصب ابزار تحلیل داده ها به این پست مراجعه نمایید: http://www.econometrics.blogfa.com/post/17) پس از نصب نیز باید مراحل زیر را انجام دهید:1-متغیرها را به صورت ستونی در اکسل وارد نمایید.(ستون ها نام متغیر و سطرها مشاهدات هر یک از متغیرها)2-مسیر زیر را دنبال کنید تا جعبه ابزار تحلیل داده های اکسل را باز کنید:DATA[menu]----->Data Analysis3-گزینه Regression را در جعبه ابزار انتخاب نمایید.4-در قسمت Input Y Range داده های متغیر وابسته را وارد نمایید.5- در قسمت Input X Range داده های متغیرهای توضیحی را وارد نمایید.6-گزینه OK را کلیک کنید برای دانلود فیلم آموزشی انجام رگرسیون چند متغیره بر روی لینک زیر کلیک نمایید:دانلود فیلم آموزشی
تحلیل مسیر در spss
در تحلیل رگرسیون خطی چند متغیره قصد داریم رابطه خطی بین متغیرهای مستقل و متغیرهای وابسته را پیش بینی کنیم . اما موضوعی که در اجرای روش تحلیل رگرسیون مطرح است ، این است که در آن ما فقط می توانستیم تاثیر مستقیم هر یک از متیغیرهای مستقل بر متغیر وابسته را پیش بینی کنیم و امکان شناسایی تاثیرات غیر مستقیم متغیرهای مستقل بر متغیر وابسته فراهم نبود . در چنین حالتی ، نمی توانیم مدل مفهومی و نظری تحقیق را که معمولاً یک مدل نظری متشکل از ساخت روابط بین متغیرهای مستقل است، مورد آزمون قرار دهیم. برای رفع چنین مشکلی ، می توانیم از روش تحلیل مسیر استفاده کنیم. بنابراین، تحلیل مسیر که برای نخستین بار توسط سوول رایت در سال 1934 توسعه یافت ، تعمیم یافته روش رگرسیون چند متغیره در ارتباط با تدوین مدل های علی است. تحلیل مسیر یک روش پیشرفته آماری است که به کمک آن می توانیم علاوه بر تاثیرات مستقیم، تاثیرات غیر مستقیم هر یک از متغیرهای مستقل بر متغیر وابسته را نیز شناسایی کنیم . بنابراین، مهم ترین مزیتی که استفاده از رو ش تحلیل مسیر نسبت به روش رگرسیون دارد ، این است که در روش تحلیل رگرسیون ، تنها قادر به شناسایی تاثیر مستقیم هر متغیر مستقل بر متغیر وابسته بودیم ، اما در روش تحلیل مسیر علاوه بر تاثیر مستقیم، امکان شناسایی تاثیرات غیر مستقیم هر یک از متغیرهای مستقل بر متغیر وابسته نیز وجود دارد. به همین خاطر ، در تحلیل مسیر ، با چندین معادله خط رگرسیونی استاندارد شده مواجه هستیم، در حالی که در تحلیل رگرسیون ، تنها یک معادله خط رگرسیونی استاندارد شده داریم. شکل های زیر به وضوح تفاوت بین تحلیل رگرسیون و تحلیل مسیر را نشان می دهند. در شکل اول، که روش تحلیل رگرسیون را نشان می دهد ، x2تنها به صورت مستقیم بر x4تاثیر دارد. اما در شکل دوم ، که روش تحلیل مسیر را نشان می دهد ، ملاحظه می گردد که x2هم به صورت مستقیم و هم به صورت غیر مستقییم از طریق x3بر x4تاثیر دارد. از طرفی، در تحلیل مسیر ما می توانیم میزان کاذب بودن روابط بین متغیرها را نشان دهیم. یعنی چقدر از این روابط ناشی از متغیرهای مستقل مورد نظر و چقدر ناشی از متغیرهای خارج از تحلیل ماست. در تحلیل مسیر فلشها مشخص کننده تاثیرات علی از متغیرهای مستقل به سمت متغیرهای وابسته میانی و نهایی می باشند. تحلیل مسیر مشخص می کند اثر هر متغیر تا چه حد مستقیم و تا چه حد غیر مستقیم است. بدین ترتیب ، تحلیل مسیر به طریقی قابل فهم ، اطلاعات زیادی درباره فرآیندهای علی فراهم می آورد. به عبارتی تکنیک تحلیل مسیر برای تعیین اثر مستقیم و غیر مستقیم و بی اثری بین متغیرهای موجود در نظام علی و ...
رگرسیون
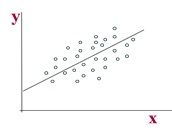
انواع رگرسیون تحلیل رگرسیون ساده یا دو متغیره : رگرسیون به معنای بازگشت است؛ یعنی چگونه نمره های Y به نمره های X بازگشت پیدا می کند. بر این اساس تحلیل رگرسیون این امکان را به ما می دهد تا تغییرات متغیر وابسته را از طریق متغیرهای مستقل پیش بینی، و سهم هر یک از متغیرهای مستقل را در تبیین متغیر وابسته تعیین کنیم. بنابراین دو نقش عمده ای که رگرسیون در تحقیق دارد"پیش بینی" و "تبیین" است. ﺿﺮﻳﺐ رﮔﺮﺳﻴﻮن ﺑﺮآورد ﻣﻘﺪار ﺗﺎﺛﻴﺮ ﻣﺘﻐﻴﺮ ﻣﺴﺘﻘﻞ ﺑﺮ ﻣﺘﻐﻴﺮ واﺑﺴﺘﻪ اﺳﺖ. ﻳﻌﻨﻲ ﺑـﺎ اﻓـﺰاﻳﺶ ﻫﺮ واﺣﺪ ﻣﺘﻐﻴﺮ ﻣﺴﺘﻘﻞ ﻧﻤﺮه ﻣﺘﻐﻴﺮ واﺑﺴﺘﻪ ﺑـﻪ اﻧـﺪازه ﭼﻨـﺪ واﺣـﺪ ﺗﻐﻴﻴـﺮ ﻣـﻲﻛﻨـﺪ. ﺿﺮاﻳﺐ رﮔﺮﺳﻴﻮن ﺟﺰﻳﻲ یا ساده ﻧﺸﺎن دﻫﻨﺪه ﻣﻘـﺪار ﺗﺎﺛﻴﺮ ﻣﺴﺘﻘﻞ ﻫﺮ ﻣﺘﻐﻴﺮ ﻣﺴﺘﻘﻞ ﺑﺮ ﻣﺘﻐﻴﺮ واﺑﺴﺘﻪ اﺳﺖ. در این حالت تنها یک متغیر مستقل وجود دارد و رابطه متغیر مستقل با وابسته خطی باشد که به آن رگرسیون ساده اطلاق می شود. در واقع اگر متغیر وابسته و مستقل تحقیق دارای سطح سنجش فاصله ای یا نسبی باشد، از تحلیل رگرسیون ساده یا دو متغیره استفاده می شود. خط رگرسیون نیز خطی است که با بهترین برازش از میان نقاط نمودار پراکنش می گذرد. معادله رگرسیون خطی بدین صورت است: Y=a+bx در این فرمول، Y نمره های پیش بینی شده متغیر وابسته، X نمره های متغیر مستقل، a مقدار ثابت عرض از مبدأ و b ضریب رگرسیون است. مقدار ثابت عرض از مبدأ: نقطه ای است که در آن خط رگرسیون محور Y را قطع می کند. ضریب رگرسیون یا شیب خط: میزان تغییر در Y را به ازای یک واحد تغییر در X نشان می دهد. این آماره همواره بر حسب واحد سنجش متغیرY بیان می شود. تحلیل رگرسیون چند متغیره: بر خلاف تحلیل رگرسیون دو متغیره که در آن یک متغیر مستقل وجود داشت، در تحلیل رگرسیون چند متغیره می توان از چند متغیر مستقل برای تبیین متغیر وابسته کمک گرفت. پس تحلیل رگرسیون چند متغیره روشی است برای تحلیل مشارکت جمعی و فردی دو یا چند متغیر مستقل Xi، در تغییرات متغیر وابسته Y. این تحلیل علاوه بر پیش بینی به تبیین نیز می پردازد. بنابراین بر حسب نحوه کاربرد آن، دو نوع معادله برای تحلیل رگرسیون وجود دارد: نخست: برای پیش بینی یک متغیر وابسته از طریق متغیرهای مستقل از معادله رگرسیونی زیر استفاده می شود. Y=a+b1x1+b2x2+...+bkxk دوم: برای تبیین واریانس متغیر وابسته از روی متغیرهای مستقل، یا به عبارتی بهتر، ارزیابی اثر نسبی هر یک از متغیرهای مستقل بر متغیر وابسته، معادله اندکی تغییر می ...
رگرسیون چند متغیره
رابطهء موجود بین سه متغیر یا بیشتر را رگرسیون چند متغیری می نامند. در رگرسیون چند متغیری، یک متغیر را وابسته و متغیرهای دیگر را مستقل می نامند. مانند آنچه در رگرسیون خطی ساده نیز گفته شد، در رگرسیون چند متغیری نیز هرگز نمی توان گفت که یک تابع ریاضی از خصوصیات متغیرهایی که به طور عادی وجود دارد به دست می آید، ولی همین نکته که بتوان متوجه شد یکی از این تابع ها تصویر خوبی بین متغیرها بیان می کند برای محقق ایده آل است.لینک اوللینک دوم
روش های چند متغیره در spss
با توجه به اینکه در پژوهش های پیش روی ما در دنیای واقعی همواره با تعداد زیادی متغیر سر و کار داریم. این امر آشنایی و استفاده از روش های چند متغیره را برای ما ناگزیر می سازد. یکی از اولین مراحل اجرای پژروهش در مواردی که خواهان طراجی ژرسشنامه هستیم تحلیل اکتشافی است که در ان موخواهیم تعداد زیادی سوالات را به چند شاخص یا عامل مهم دسته بندی نماییم. برای این کار از تحلیل عاملی اکتشافی استفاده میکنیم. در ادامه یک جزوه مناسب که هم ژایه نظری و هم نحوه اجرای این امر را در نرم افزار محبوب spss به صورت تصویری آورده است را برای شما دوستان عزیز قرار داده ام. امید است که مورد استفاده قرار گیرد. دانلود فایل
رگرسیون و مدل سازی به روش حداقل مربعات جزئی (Partial Least Square)
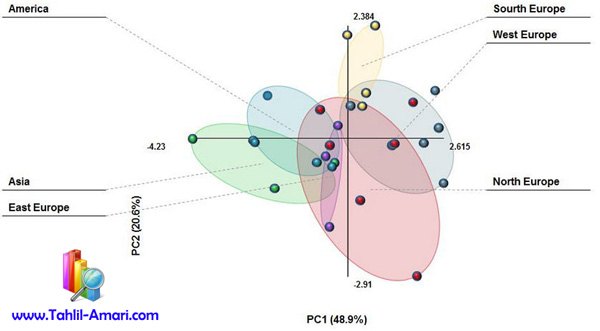
رگرسیون و مدل سازی به روش حداقل مربعات جزئی (Partial Least Square)روش حداقل مربعات جزئی (Partial Least Square) به عنوان یک جایگزین برای روش های OLS رگرسیون، Canonical رگرسیون و مدل سازی معادلات ساختاری (SEM) در پژوهش هایی که متغیرهای مستقل و وابسته وجود دارد، بکار گرفته می شود. روش PLS در اغلب اوقات، معادلات ساختاری مبتنی بر مولفه (Component-Based SEM) نامیده می شود در حالی که روش معادلات ساختاری مبتنی بر کواریانس است(Covariance-Based SEM).این روش زمانی استفاده می شود که می خواهیم تاثیرات چندین متغیر مستقل را بر یک یا چند متغیر وابسته بررسی کنیم اما پیش فرض های انجام رگرسیون یا معادلات ساختاری بر قرار نیست و یا اینکه در پژوهش به مشکلات زیر مواجه شویم: چندین متغیر وابسته داشته باشیم.تعداد متغیرهای مستقل زیاد باشد و شناسایی متغیرهای تاثیر گذار مشکل باشد. در متغیرهای مستقل هم خطی وجود داشته باشد(Multicollinearity) حجم نمونه کم باشد. در رگرسیون توزیع فروانی متغیرها نرمال نباشد و یا در روش معادلات ساختاری نرمال بودن چند متغیره برقرار نباشد.روش حداقل مربعات جزئی می تواند تاثیرات متغیرهای مستقل را بر متغیر وابسته بصورت یک مدل رگرسیونی یا مدل ساختاری برازش کند. چنانچه هدف پژوهشگر پیش بینی یا مدل سازی اکتشافی باشد استفاده از روش PLS توصیه می شود. روش مدل سازی معادلات ساختاری(SEM) برای مقاصد تایید مدل کاربرد دارد و برای براورد پارامترهای مدل نیازمند حجم نمونه زیاد و برقرار بودن پیش فرض نرمال بودن چند متغیره است اما روش PLS چون برای مقاصد اکتشافی کاربرد دارد به هیچ گونه پیش فرضی احتیاج ندارد . در برخی از منابع ذکر شده است روش PLS با حداقل ۳۰ نمونه نیز قابل انجام است و نتایج در مقابل داده های مفقود شده(Missing value) پایدار است.از لحاظ تکنیکی فرق روش PLS با سایر روش های رگرسیونی است این است که به جای در نظر گرفتن متغیرهای مستقل، از طریق تکنیک تحلیل مولفه های اصلی(PCA) متغیرهای مستقل در چند عامل کلی تر قرار می گیرند به گونه ای که این عامل ها بیشترین تغییرات متغیر(های) وابسته را تبیین کنند•برای انجام تحلیل پروژه اماری خود توسط نرم افزار spssدر کمتر از 3 روز و یا در صورت اضطراری کمتر،با شماره زیر تماس بگیرید. • 09371559986•[email protected]•
رگرسیون و مدل سازی به روش حداقل مربعات جزئی (Partial Least Square)
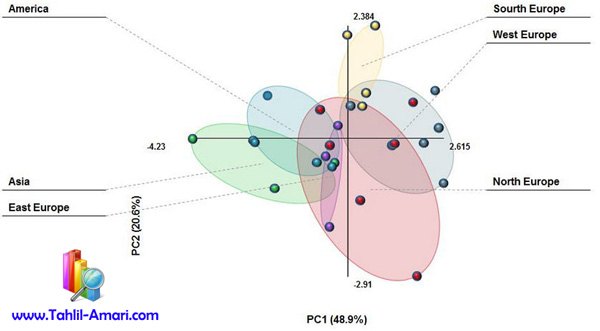
رگرسیون و مدل سازی به روش حداقل مربعات جزئی (Partial Least Square) روش حداقل مربعات جزئی (Partial Least Square) به عنوان یک جایگزین برای روش های OLS رگرسیون، Canonical رگرسیون و مدل سازی معادلات ساختاری (SEM) در پژوهش هایی که متغیرهای مستقل و وابسته وجود دارد، بکار گرفته می شود. روش PLS در اغلب اوقات، معادلات ساختاری مبتنی بر مولفه (Component-Based SEM) نامیده می شود در حالی که روش معادلات ساختاری مبتنی بر کواریانس است(Covariance-Based SEM). این روش زمانی استفاده می شود که می خواهیم تاثیرات چندین متغیر مستقل را بر یک یا چند متغیر وابسته بررسی کنیم اما پیش فرض های انجام رگرسیون یا معادلات ساختاری بر قرار نیست و یا اینکه در پژوهش به مشکلات زیر مواجه شویم: چندین متغیر وابسته داشته باشیم. تعداد متغیرهای مستقل زیاد باشد و شناسایی متغیرهای تاثیر گذار مشکل باشد. در متغیرهای مستقل هم خطی وجود داشته باشد(Multicollinearity) حجم نمونه کم باشد. در رگرسیون توزیع فروانی متغیرها نرمال نباشد و یا در روش معادلات ساختاری نرمال بودن چند متغیره برقرار نباشد. روش حداقل مربعات جزئی می تواند تاثیرات متغیرهای مستقل را بر متغیر وابسته بصورت یک مدل رگرسیونی یا مدل ساختاری برازش کند. چنانچه هدف پژوهشگر پیش بینی یا مدل سازی اکتشافی باشد استفاده از روش PLS توصیه می شود. روش مدل سازی معادلات ساختاری(SEM) برای مقاصد تایید مدل کاربرد دارد و برای براورد پارامترهای مدل نیازمند حجم نمونه زیاد و برقرار بودن پیش فرض نرمال بودن چند متغیره است اما روش PLS چون برای مقاصد اکتشافی کاربرد دارد به هیچ گونه پیش فرضی احتیاج ندارد . در برخی از منابع ذکر شده است روش PLS با حداقل ۳۰ نمونه نیز قابل انجام است و نتایج در مقابل داده های مفقود شده(Missing value) پایدار است. از لحاظ تکنیکی فرق روش PLS با سایر روش های رگرسیونی است این است که به جای در نظر گرفتن متغیرهای مستقل، از طریق تکنیک تحلیل مولفه های اصلی(PCA) متغیرهای مستقل در چند عامل کلی تر قرار می گیرند به گونه ای که این عامل ها بیشترین تغییرات متغیر(های) وابسته را تبیین کنند
کاربرد آنالیز رگرسیون خطی(Linear Regression) با استفاده از نرم افزار SAS
با توجه به سوالات مکرر دانشجویان در مورد نحوه محاسبه رگرسیون خطی در نرم افزار SASبر آن شدم تا محاسبه روش محاسبه این آزمون را به طور مختصر در این نوشتار ارائه دهم. اصولا کاربرد رگرسیون در مطالعات مختلف بسیار وسیع است و کمتر تحقیقی را می توان یافت که از رگرسیون ها برای پیش بینی ها استفاه نکرده باشد. خانواده رگرسیون ها بسیار گسترده بوده و دارای انواع مختلفی است که یکی از پر کاربرد ترین آنها، نوع خطی است. نرم افزا SAS به عنوان قویترین نرم افزار آمار مورد استفاده در بین محققان، کامل ترین روش محاسبه رگرسیون خطی را ارائه می دهد که محقق می تواند با توجه به نیاز خود از آن استفاده کند. نرم افزار SAS دارای محیط برنامه نویسی بسیار پیشرفته و کاملی است که تمام نیاز های آماری محققان را در سطوح مختلف برآورده می کند. در این نوشتار از ارائه فرمول ها پرهیز شده و سعی بر ارائه یک راهنمای کاربردی برای استفاده از این روش آماری در نرم افزار SASبود. انجام رگرسیون خطی چندگانه دارای پیش فرض هایی است که باید این قواعد را برای کسب نتیجه بهینه مورد توجه قرار داد. استقلال مشاهدات، ساختار کوواریانس عمومی در بین مشاهدات، همگونی واریانس های وضعیت خطاها بر متغیر های پیش بین و نرمال بودن توزیع چند متغیره باقیمانده ها. در مورد نرمال بودن توزیع چند متغیره، در نرم افزار هایی چون SPSS و SAS آزمون خاصی ارائه نمی شود و صرفا از طیق اسکتر پلات ها نحوه توزیع باقیمانده و نرمال بودن آن مورد قضاوت قرار می گیرد. در مورد همگونی واریانس های وضعیت خطاها بر متغیر های پیش بین، با توجه به اینکه اکثر ازمون های ارائه شده به نرمال بودن توزیع وابسته هستند؛ برای این منظور نرم افزار SAS از آماره F برای برازش کلی مدل رگرسیونی استفاده می کند. معنی داری آزمون F به معنای تحقق این پیش فرض رگرسیون خطی چند گانه است. برای آزمون هم خطی در رگرسیون از مقدار تولرانس یا تورش واریانس استفاده می شود که به این معنا است که اطلاعات هر متغیر پیش بین وارد شده به مدل تا چه حد توسط سایر متغیرهای مستقل قابل برآورد بوده است. برای این منظور بایدبه شاخص شرایط استناد نمود که باید مقدار آن زیر 15 برای مدل های خوب باشد و تا 30 قابل تحمل است لیکن مقادیر کمتر آن به معنای اعتبار بیشتر ضریب تعیین است. برای بررسی استقلال خطاها از یکدیگر نیز از آزمون دوربین واتسون استفاده می شود که باید بین 5/1 تا 5/2 باشد. در اینجا هدف بررسی حل یک مثال واقعی با نرم افزار SAS است. در نظر بگیرید محققی علاقه مند است تا بداند در دفعات مشاهده و یادآوری یک تیزر تلویزیونی، نقش متغیر هایی چون آشکار بودن پیام آن، منطقی بودن عناصر به ...
