حل معادله درجه 3
روش های حل معادله درجه 3
از فایل زیر می توانید 31 روش مختلف برای حل معادله درجه 3 را دانلود کنید.(نویسنده آقای سیدمحمد رضا هاشمی موسوی)کلیک کنید.
حل آسان معادله درجه 3
حل معادلات درجه سوم آسان شد! Cubic Formula versus Quadratic Formula آنچه در زیر میخوانید خلاصه ی تحقیقی است که من در حدود دو سال پیش بر روی معادلات درجه سوم انجام دادم و نتیجه ی آنرا در یک مقاله ی تقریبا" بیست صفحه ای در اکتبر گذشته در یک کنفرانس ریاضی در شمال غرب کانادا عرضه نمودم. این کنفرانس که همه ساله در ماه اکتبر در غرب کانادا برگزار میشود و بمدت سه روز ادامه دارد از جمله کنفرانس های خوب و معتبر ریاضی آمریکای شمالی است که در حدود دو هزار تن از ریاضی دانان، اساتید، دانشجویان و دبیران ریاضی از سراسر نقاط دنیا( ولی بیشتر از آمریکا و کانادا ) را به خود جلب میکند. این کنفرانس در حدود دویست "کارگاه" دارد که هر کدام بین یک تا سه ساعت طول میکشد. تقریبا" دویست سخنران در این کارگاه ها سخنرانی میکنند و حاصل تحقیقات یا تجربیات خود در زمینه ی آموزش ریاضیات( از کلاس اول دبستان تا کالج) را بر شرکت کنندگان در کنفرانس عرضه میدارند. همچنین موسسات انتشاراتی کتابهای ریاضی و شرکتهای سازنده ی ماشین های حسابگر و ابزارهایی که در راه آموزش ریاضیات در کلاسهای درس بکار برده میشوند آخرین آثار و اختراعات و ابداعات خود را به معرض نمایش میگذارند. کنفرانس امسال در شهر ویکتوریا، مرکز استان بریتیش کلمبیا برگزار شد. من در سخنرانی خود با عنوان "حل معادلات درجه سوم آسان شد"، نخست مروری داشتم بر تاریخچه حل معادله درجه سوم از آغاز تا امروز. برای من باعث مباهات بود که به شرکت کنندگان در این کنفرانس ، از عمر خیام به عنوان یکی از پیشروان حل معادلات درجه سوم بگویم و به تشریح روش هندسی این ریاضیدان بزرگ که تقریبا" هزار سال پیش ریشه ی مثبت یکدسته از معادلات درجه سوم را از طریق برخورد یک دایره و یک سهمی پیدا نمود، بپردازم. نیز از همکاری خیام در ایجاد تقویم جلالی و مقایسه دقت آن با تقویم گره گوری یاد نمودم. همچنین از تلاشهای موفقیت آمیز ریاضیدانان قرن شانزدهم ایتالیا در حل معادلات درجه سوم ذکری به میان آوردم. پس از آن به تشریح جزئیات تحقیقات ویافته های خود پرداختم. (در نظر داشتم و از قبل هم آماده کرده بودم که در پایان سخنرانی ام چند رباعی از خیام، از آن رباعی هایی که بیشتر مورد پسند ملل مغرب زمین است، برای حضار با آواز بخوانم، به همان شکل که در بوستان شعر و آواز خوانده ام ولی متاسفانه وقت اجازه نداد.) اصل مقاله قرار است که در سال 2007 در یکی از ژورنال های ریاضی کانادا منتشر شود، در آنوقت آنرا ترجمه خواهم کرد و در این وبلاگ به نظر گرامی شما خواهم رساند. عجالتا" خلاصه مقاله را در زیر ملاحظه بفرمایید. همین خلاصه هم، خود برای حل هر نوع معادله درجه سوم یک مجهولی کافی ...
حل معادله ی درجه ی 3
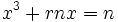
تاریخچه معادلات درجه سوم برای اولین بار توسط ریاضیدانان هندسی در حدود 400 سال قبل از میلاد مورد توجه قرار گرفت. در بین ریاضیدانان پارسی، عمر خیام (1123-1048) راه حلی را برای حل معادله درجه سوم ابداع کرد. او در این روش با استفاده از هندسه نشان داد که چگونه با استفاده از روش هندسی میتوان به جواب عددی معادله رسید با استفاده از جدول مثلثاتی. همچنین در حول و حوش قرن 16، یک ریاضیدان ایتالیایی به نام scipione، روشی را برای حل کلاسی از معادلات درجه سوم که به صورت میباشند را ادامه داد. او همچنین نشان داد که تمامی معادلات درجه سوم را میتوان به صورت گفته شده کاهش داد.ریشههای معادله هر معادله درجه سوم حقیقی حداقل یک جواب حقیقی دارد. این استدلال نتیجه مستقیم قضیه مقدار میانگین است. برای معادله درجه سوم یک معادله مشخصهای به صورت زیر بیان میشود که امکان وجود ریشهها را بیان میکند. بنابراین با فرض موارد زیر نتجه میشود: : آنگاه معادله حتما 3 ریشه مجزا خواهد داشت. : آنگاه معادله حتما یک ریشه حقیقی و. یک جفت ریشه مختلط خواهد داشت. : آنگاه معادله حداقل دو ریشه دارد. برای تصمیم گیری در مورد اینکه معادله چند ریشه متمایز دارد را به صورت زیر تشکیل میدهیم: حال دو حالت در نظر میگیریم: اگر ، آنگاه هر 3 ریشه تکراری است. در غیر اینصورت معادله 2 ریشه تکراری و یک ریشه مجزا خواهد داشت. روش کاردانو برای پیدا کردن ریشههای معادله درجه سوم در ابتدا معادله داده شده را به فرم کلاسیک تبدیل میکنیم، همین معادله داده شده را به ضریب تقسیم میکنیم. حال با تغییر متغیر: معادله را به فرم زیر تبدیل میکنیم. بطوری که و معادله به دست آمده را معادله تقلیل یافته مینامیم. حال فرض میکنیم که بتوانیم اعداد u و v را طوری پیدا کنیم که: حل جواب معادله داده شده با فرض t=v-u به دست میآید این مطلب بطور مستقیم با تعقیب متغیر t در (2) قابل بررسی میباشد. به عنوان یک نتیجه از اتحاد معادله درجه سوم معادله (3) قابل حل است. با حل معادله درجه دوم برای v که به دست میآید با قرار دادن این مقادیر در 3 خواهیم داشت که از حل این معادله که یک معادله درجه 2 از میباشد خواهیم داشت حال چون و پس
حل معادلات درجه سوم آسان شد!
حل معادلات درجه سوم آسان شد! Cubic Formula versus Quadratic Formula <?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" />آنچه در زیر میخوانید خلاصه ی تحقیقی است که من در حدود دو سال پیش بر روی معادلات درجه سوم انجام دادم و نتیجه ی آنرا در یک مقاله ی تقریبا" بیست صفحه ای در اکتبر گذشته در یک کنفرانس ریاضی در شمال غرب کانادا عرضه نمودم. این کنفرانس که همه ساله در ماه اکتبر در غرب کانادا برگزار میشود و بمدت سه روز ادامه دارد از جمله کنفرانس های خوب و معتبر ریاضی آمریکای شمالی است که در حدود دو هزار تن از ریاضی دانان، اساتید، دانشجویان و دبیران ریاضی از سراسر نقاط دنیا( ولی بیشتر از آمریکا و کانادا ) را به خود جلب میکند. این کنفرانس در حدود دویست "کارگاه" دارد که هر کدام بین یک تا سه ساعت طول میکشد. تقریبا" دویست سخنران در این کارگاه ها سخنرانی میکنند و حاصل تحقیقات یا تجربیات خود در زمینه ی آموزش ریاضیات( از کلاس اول دبستان تا کالج) را بر شرکت کنندگان در کنفرانس عرضه میدارند. همچنین موسسات انتشاراتی کتابهای ریاضی و شرکتهای سازنده ی ماشین های حسابگر و ابزارهایی که در راه آموزش ریاضیات در کلاسهای درس بکار برده میشوند آخرین آثار و اختراعات و ابداعات خود را به معرض نمایش میگذارند. کنفرانس امسال در شهر ویکتوریا، مرکز استان بریتیش کلمبیا برگزار شد. من در سخنرانی خود با عنوان "حل معادلات درجه سوم آسان شد"، نخست مروری داشتم بر تاریخچه حل معادله درجه سوم از آغاز تا امروز. برای من باعث مباهات بود که به شرکت کنندگان در این کنفرانس ، از عمر خیام به عنوان یکی از پیشروان حل معادلات درجه سوم بگویم و به تشریح روش هندسی این ریاضیدان بزرگ که تقریبا" هزار سال پیش ریشه ی مثبت یکدسته از معادلات درجه سوم را از طریق برخورد یک دایره و یک سهمی پیدا نمود، بپردازم. نیز از همکاری خیام در ایجاد تقویم جلالی و مقایسه دقت آن با تقویم گره گوری یاد نمودم. همچنین از تلاشهای موفقیت آمیز ریاضیدانان قرن شانزدهم ایتالیا در حل معادلات درجه سوم ذکری به میان آوردم. پس از آن به تشریح جزئیات تحقیقات ویافته های خود پرداختم. (در نظر داشتم و از قبل هم آماده کرده بودم که در پایان سخنرانی ام چند رباعی از خیام، از آن رباعی هایی که بیشتر مورد پسند ملل مغرب زمین است، برای حضار با آواز بخوانم، به همان شکل که در بوستان شعر و آواز خوانده ام ولی متاسفانه وقت اجازه نداد.) اصل مقاله قرار است که در سال 2007 در یکی از ژورنال های ریاضی کانادا منتشر شود، در آنوقت آنرا ترجمه خواهم کرد و در این وبلاگ به نظر گرامی شما خواهم رساند. عجالتا" خلاصه مقاله را در زیر ملاحظه بفرمایید. همین خلاصه ...
حل معادله درجه سوم
حل معادله درجه سوم ( از Telour.ir) راهی جدید برای حل معادله درجه ی سوم راه حل کاردان حل معادله درجه ی سوم از دو جهت مورد توجه است؛ زیرا نه تنها به جهت درستی خودش جالب است بلکه این روش راه حلی است برای حل معادله ی درجه ی چهارم. این نوشته پنج متغیر اصلی معادله درجه سوم را توصیف می کند و نشان می دهد چگونه این پنج متغیر به تبدیلات اصلی نمونه های استاندارد حل معادله ی درجه ی 3 وابسته است که عموما با نام روش کاردان (cardan's solution) شناخته می شود. جیرو لامو کاردانو کاردان که یکی از با استعدادترین مردان زمان خود و در چندین فن جامع بود، آثاری درباره ی حساب، نجوم، فیزیک،طب و دیگر موضوعات از خود بر جای گذاشت. بزرگترین اثر وی، آرس ماگنا، اولین رساله ی عظیم به زبان لاتین است که صرفا به جبر اختصاص دارد. در آن رساله به وجود ریشه های منفی یک معادله پی برده شده و به محاسبه با اعداد موهومی تا حدی توجه شده است. در این اثر همچنین روش خاصی برای به دست آوردن یک مقدار تقریبی برای ریشه ی معادله ای از درجه ی دلخواه وجود دارد . راه حل معادله ی درجه ی سوم که توسط کاردان در آرس ماگنای وی داده شده، به صورت زیر می باشد: اتحاد را در نظر بگیرید. اگر a و b را چنان اختیار کنیم که در این صورت x با a-b برابر است. با حل دو معادله ی اخیر به طور همزمان برحسب a و b داریم و بدین ترتیبx معین می شود. طبق تعريف یک نقطه روی منحنی چند جمله ای با درجه ی است که با حرکت در راستای محور و با جایگزینی مجموع ریشه های منحنی جدید مساوی صفر می شود. در معادله ی چند جمله ای: می توان به راحتی نشان داد که اگریک چند جمله ای درجه 3 باشد پس به عنوان معادله ی درجه 3 تنزل یافته شناخته می شود و یک نقطه ی عطف است. حال معادله ی عمومی درجه 3 را مشاهده کنید: در این جا برابر و نقطه ی تقارن معادله ی درجه ی 3 می باشد. پارامترهای به عنوان فواصل در شکل نشان داده شده است. روابط و با عبارت است از: این نتایج به راحتی توسط تعیین مکان نقاط بازگشتی (نقطه عطف) بدست خواهند آمد. از این معادلات به راحتی می توان فهمید که شمائل کلی معادله ی درجه 3 توسط پارامتر مشخص می شود. در این شکل یا نقاط ماکزیمم و مینیمم با هم وجود خواهند داشت، به عبارت ديگر: یا درN منطبق هستند: و یا نمودار دارای نقطه ی عطف نیست. به علاوه می توان نوشت رابطه ی یک مورد مخصوص از قضیه ی کلی زیر است : اگر منحنی چند جمله ای از مبدا عبور کند ریشه های ایجاد شده ی آن (به جز ) با مختصات x نقاط بازگشتی با رابطه ی زیر مرتبط است: حل معادله ی درجه سوم: علاوه بر ارزش ترسیم منحنی، پارامتر های به طور کامل روشی استاندارد را برای حل معادله ی درجه ی 3 ارائه می کنند. ...
حل معادله درجه دوم
این فرمول حل معادله درجه دوم یا همان فرمول دلتا است که با حل یک مثال آوردم:
حل معادله درجه 3 و 4
حل معادله درجه 3 و 4
روش خیام(هندسی) در حل معادله درجه 3
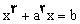
حدود 900 سال پیش ،خیام روشی هندسی برای حل معادله ي درجه ي سوم به شكل: () ارائه کرد که در اين جا به آن پرداخته ايم: 1)ابتدا یک سهمی به معادله ي را رسم می کنیم.2)دایره اي به قطر رسم می کنیم ،به طوری که مرکز آن روی محور xها قرار داشته ودایره بر محور yها مماس باشد.(مانند آن چه که در شکل زیر آمده است.) 3)دایره ي رسم شده،سهمی رادرنقطه ي P قطع می کند،از P عمودی برمحور xها رسم کرده و نقطه ي تقاطع را Q می ناميم.اندازه ي پاره خط AQ ريشه ي معادله است. اثبات:معادله ي دايره ي به مركزو شعاع عبارت است از:.اگر اين دايره را با سهميقطع دهيم به معادله ي مي رسيم و اين يعني اندازه ي پاره خط AQ ريشه ي معادله ي درجه ي سوم مزبور است.
