حل دستگاه معادلات غیر خطی
روش نیوتن در حل دستگاه معادلات جبری 1
اصول حل دستگاه معادلات غیر خطی به روش نیوتن هم مثل حل یک معادله است اما با این تفاوت که بجای مشتق معادله باید ژاکوبی دستگاه معادلات رو که در واقع دستگاه مشتقات جزئی معادلات بر حسب متغیرهاست رو محاسبه و استفاده کنیم. برای حل تکراری معادلات، ابتدا یک حدس اولیه را در نظر می گیریم و سپس با استفاده از رابطه تکرار (رابطه زیر) حدس خود را بهبود می دهیم تا به نتیجه مورد نظر خود برسیم. داریم در اینجا x ها بردار هستند، از طرفی می دانیم که: ماتریس ژاکوبی J را بصورت زیر تعریف می کنیم با داشتن رابطه بالا روند تکراری حل معادله را بصورت زیر می نویسیم: کد فرترن روش بالا را می توانید در آدرس زیر بیابید: 9.6 Newton-Raphson Method for Nonlinear Systems of Equations 372 این کد فرض می کند که شما ماتریس ژاکوبی را محاسبه نموده اید، در صورتیکه مشتق گیری و تشکیل ماتریس ژاکوبی دشوار باشد میتوانید آنرا بصورت عددی محاسبه نمایید، برای اینکار بخش زیر را ببینید: 9.7 Globally Convergent Methods for Nonlinear Systems of Equations 376 همچنین در کد بالا از تابع حل دستگاه معادلات خطی استفاده شده است و شما می توانید کد این تابع را در بخش زیر ببینید: 2.3 LU Decomposition and Its Applications 34 برای دیدن فیلهای بالا ممکن است لازم باشد پلاگین زیر را در دانلود کرده و در فولدر نصب Adobe acrobet کپی کنید. http://www.nr.com/plugin/winapi/FileOpen.api درصورتی که کد این بخش را با موفقیت نوشتید مرا هم مطلع نمایید تا کلی به شما افتخار کنم پیروز و سربلند باشید
حل عددی معادلات غیر خطی _ روش تیلور
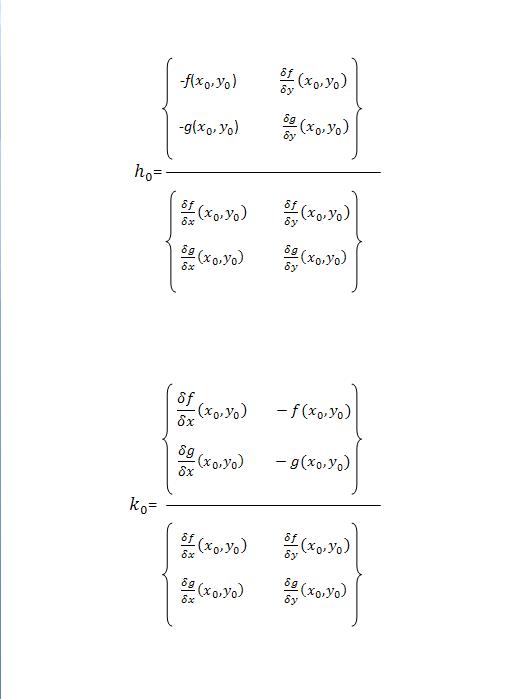
به عنوان مثال می خواهیم با استفاده از روش تیلور دستگاه معادلات غیر خطی زیر را حل کنیم:f(x,y)=x^2+y-11g(x,y)=x+y^2-7x0=3.5y0=1.5الگوریتم روش تیلور به صورت:x1=x0+h0y1=y0+k0حل به کمک برنامه :(x,y]=taylor_method(f,g,x0,y0,i]که i معرف تعداد تکرار میباشدsyms x y<<f=x^2+y-11<< g=x+y^2-7<< (x,y]=taylor_method(f,g,3.5,1.5,2]<<=x1 2.967249950288328 =y1 2.000514515808312 برای دریافت فایل کلیک کنیدMohandesaan.Blogfa.com
دانلود نرم افزار ترمودینامیکی و آموزش EES
EES مخفف Engineering Equation Solver است. ساده¬ترین قابلیت EES حل دستگاه معادلات جبری (شامل معادلات غیر خطی) است. همچنین EES می تواند معادلات دیفرانسیل و معادلات مختلط را حل کند، محاسبات بهینه سازی ، رگرسیون خطی و غیرخطی، رسم نمودار با دقت بالا و تحلیل عدم اطمینان را انجام دهد و حتی انیمیشن های مهندسی بر پایه محاسبات بسازد.ایده اصلی برای نوشتن EES آموزش ترمودینامیک و انتقال حرارت می باشد، برای اینکه دانشجویان این مباحث را بیاموزند باید مسائل زیادی حل کنند، اما در هر مسئله بیشتر وقت برای میانیابی خواص و استفاده از معادلات به ترتیب صحیح تلف می گردد. وقتی دانشجو مباحث را فهمید و با کار با جداول ترمودینامیکی آشنا شد، میانیابی داده های جدول و حل معادلات کمکی در بالا بردن دانش او نخواهد کرد. برنامه EES دانشجو را از این بخش رها خواهد کرد و اجازه می دهد که او در حل مسئله بر روی ماهیت فیزیکی و دانش مسئله متمرکز شود. دانلود
حل دستگاههای خطی N معادله با N مجهول در MATLAB
در موارد بسیاری نیاز است تا تعداد معینی معادله خطی با همان تعداد معین از مجهولات را حل کنیم. برای نمونه در زمینههایی مانند تحلیل مدارات الکترونیکی، مدلسازی آب و هوا، CT Scan (computed axial tomography) و موارد بسیار دیگر، با این مبحث ریاضی روبرو خواهیم بود. یک شکل نمونه از یک دستگاه با چهار معادله و چهار مجهول به فرم زیرمفروض است: 2a + 2b + 1c + 6d = 4 4a – 2b + 0.5c +1d = 2 6a + 1b + 0c – 1d = -1 2a + 2b – 1c + 3d = 4 در اینجا ما باید مقادیر a, b, c, d را طوری بیابیم که همه معدلات ارضاء گردند. برای حل دستگاههای معادلات خطی در مقاطع راهنمایی و دبیرستان مطالب زیادی آموختهایم. و روشهای متعددی نیز برای این امر وجود دارد. که از آن جمله می توان به روش حذفی و روش کرامر اشاره کرد. اما در محیط MATLAB دستوراتی برای حل این معادلات وجود دارد که از روش ضرب ماتریس (اسکالر) استفاده می کند. برای همین دو عدد ماتریس از طرفین معادله به فرم زیر تشکیل داده می شود: A=[2 3 1 6 4 -2 .5 1 6 1 0 -1 2 2 -1 3] B=[4 2 -1 4] حال بایستی ماتریس A معکوس گردد و سپس در ماتریس B ضرب گردد. و حاصل در یک ماتریس دیگر ذخیره گردد؛ دستورات MATLAB به فرم زیر خواهد بود: x=inv(A)*B و یا x=A^(-1)*B و نیز می توان از دستور x=A\Bاستفاده کرد که این دستور بسیار بهینه و قابل اعتماد نسبت به دو مورد قبلی است. ماتریس x که از حاصلضرب دو ماتریس اول بدست آمده یک ماتریس یک ستونه و چهار سطری می باشد که مجهولات معادلات به فرم زیر در آن جای گرفته اند: a=x(1) b=x(2) c=x(3) d=x(4) این روش در عین سادگی فوق العاده گاهی وقتها نیز دچار مشکل می شود و جوابهای صحیح را بدست نمی دهد و یا گاها چند جواب متفاوت را در متغییرهای متعدد می دهد، (مخصوصاً در زمان استفاده از دستور inv(A)) برای اجتناب و پیشگیری از این مشکل، در دستگاه معادلات، بایستی به N مجهول دقیقاً N معادله خطی مستقل داشته باشیم. و معادله مستقل معادله ای است که با افزودن یک مقدار به معدله دیگر بدست نیاید. یعنی کاملا با معدلات دیگر متفاوت باشد!. البته همیشه نمی توان با یک نگاه ساده به معادلات به مستقل بودن آنها پی برد! بنابراین در MATLAB برای حل این مشکل از دستور Rank() استفاده می کنیم که در صورت دادن ماتریس مرجع به آن، تعداد معادلات مستقل را مشخص خواهد نمود. یک مثال کاربردی در تصویربرداری پژشکی: http://homepages.udayton.edu/~hardierc/ECE203/lineareq.htmhttp://en.wikipedia.org/wiki/System_of_linear_equations
آموزش فارسی نرم افزار ایز EES
نرم افزار EES چیست و چرا بایستی آن را آموخت؟نام EES که ایز تلفظ میگردد، مخفف Engineering Equations Solver است. سادهترین قابلیت EES حل دستگاه معادلات جبری (شامل معادلات غیر خطی) است. یعنی کافی است شما معادلات و دادههای لازم برای حل یک مسئله را وارد نمایید و این نرم افزار پاسخ محاسبات را به شما خواهد داد. با پردازنده متنی موجود در EES میتوانید معادلات را همانگونه که آنها را می بینید بدون توجه به جایگاه متغیرها در برنامه وارد نمایید. همچنین EES میتواند معادلات دیفرانسیل و معادلات مختلط را حل کند، محاسبات بهینهسازی، رگرسیون خطی و غیرخطی، رسم نمودار با دقت بالا و تحلیل عدم اطمینان را انجام دهد و حتی انیمیشنهای مهندسی بر پایه محاسبات بسازد. این نرم افزار واحدهای مختلف فیزیکی را میشناسد و کنترل میکند.برنامه EES با برنامههای محاسباتی دیگر چند تفاوت عمده دارد. اول این که EES با دستهبندی معادلات، حل معادلات را در بهترین حالت تضمین میکند. دوم این که EES دارای توابع ریاضی، ترمودینامیکی و مکانیکی مفید زیادی است که میتواند محاسبات مهندسی را بسیار آسان کند و همزمان واحدهای مهندسی را در معادلات ارزیابی نماید و با این کار امکان خطا در وارد نمودن معادلات را به حداقل میرساند. سوم این که خواص ترمودینامیکی مواد زیادی بصورت داخلی در این برنامه پیادهسازی شده است. برای مثال همه خواص ترمودینامیکی جدول بخار، مایعات مبرد مختلف و بسیاری از مواد دیگر در EES قابل استفاده است. برنامه EES خواص هوا و توابع سایکرومتریک و دادههای جدول JANAF برای بسیاری از گازها و همچنین جامدات را دارا میباشد و انجام محاسبات سایکرومتریک و رسم نمودارهای آنها را بسیار ساده کرده است.توابع ریاضی و ترمودینامیکی EES بسیار متنوع است اما اگر نتواند خواستههای کاربر را ارضاء کند، این برنامه روشهایی را برای ایجاد توابع مختلف در اختیار کاربر قرار میدهد. اول امکان استفاده از دادههای جدولی، میانیابی و استفاده از آنها در برنامه است. دوم، EES امکان نوشتن توابع و زیربرنامههای مختلف را در بخش معادلات (مانند آنچه درسایر زبانهای برنامهنویسی معمول است) پشتیبانی میکند. سوم، نوشتن توابع و روندها خارجی توسط زبانهای برنامهنویسی سطح بالا مانند Pascal، FORTRAN، زبان C و VB (یا هر زبان برنامه نویسی که امکان ایجاد dll را داشته باشد) بصورت dll و فراخوانی توابع در برنامه EES میباشد. کافی است که توابع، روندها، زیربرنامهها و ماژولها را بصورت فایلهای کتابخانهای ذخیره کنیم که میتوان آنها را بصورت اتوماتیک در برنامه EES وارد کرد. همچنین این برنامه امکان اتصال و دریافت یا ارسال اطلاعات ...
