حجم اشکال هندسی
حجم ومساحت اشکال هندسی /ریاضی ششم
دانش آموزان عزیز :در ایام تعطیلات نوروز با مطالعه و تمرین بخش مساحت و حجم به اطلاعات خود در این زمینه بیفزایید حجم:(Volume) حجم در لغت به معنی برآمدگی و ستبری و جسامت چیزی می باشد و در اصطلاح هندسه گنجایش و ظرفیت جسم و آن مقداری از فضا که جسم آن را اشغال می کند, را نشان می دهد. منشور: (Prism) منشور در لغت به معنی پراکنده, نشر شده, زنده شده و مبعوث است و در اصطلاح هندسه نام شکلی است که دو قاعده دارد که دو چند ضلعی مساوی هستند و بدنه منشور(سطح جانبی منشور ) از مستطیلها یا متوازی الاضلاع ها تشکیل شده است. معرفی منشور 5 پهلو: í نام شکل: منشور 5 پهلو í یال های منشور: 'EE',DD',CC',BB',AA í وجه منشور: هر کدام از مستطیل های جانبی را یک وجه منشور می نامند. í ارتفاع منشور: از آنجا که هر کدام از یال ها بر دو قاعده منشور عمود می باشند, لذا ارتفاع منشور با اندازه هر یک از یال ها برابر است. í قاعده ی منشور: منشور دو قاعده دارد. ABCDE و 'A'B'C'D'E که دو پنج ضلعی مساوی اند. رابطه های مهم: ارتفاع × مساحت قاعده = حجم منشور ارتفاع × محیط قاعده = مساحت جانبی منشور مساحت دو قاعده + مساحت جانبی = مساحت کل منشور استوانه: (Cylinder) نام شکلی است که دو قاعده دارد که دو دایره مساوی هستند و بر جانبی راست استوار است. اگر مستطیل را حول طول آن دوران دهیم, شکل فضایی حاصل استوانه نامیده می شود. در این صورت طول مستطیل ارتفاع استوانه و عرض آن شعاع قاعده استوانه می باشد. در شکل بالا مستطیل ABCD را حول طول آن دوران داده ایم و استوانه بوجود آمده است. رابطه های مهم: ارتفاع×مساحت قاعده(دایره) = حجم استوانه ارتفاع×محیط قاعده(دایره) = مساحت جانبی استوانه مساحت دو قاعده + مساحت جانبی = مساحت کل استوانه هرم: (pyramid) هرم در لغت به معنی سخت پیر گردیدن و کلان سال شدن است و در اصطلاح هندسه حجمی است که قاعده آن یک چند ضلعی و وجوه جانبی اش مثلثهایی باشند که همه به یک رأس مشترک(رأس هرم) منتهی می شوند. معرفی هرم منتظم: í نام شکل: هرم منتظم. í رأس هرم: نقطه S í ارتفاع هرم: پاره خطی است که از رأس هرم به مرکز قاعده ی هرم عمود است(SO) í قاعده هرم: پنج ضلعی منتظم ABCDE í سهم هرم: ارتفاع مثلث های جانبی, ارتفاع هر وجه جانبی هرم منتظم(SH). í وجه هرم: هر یک از مثلث هایی که بدنه هرم را می پوشانند را یک وجه جانبی می نامیم. í یال هرم: محل تقاطع هر دو وجه جانبی را یال هرم می نامیم. SE,SD,SC,SB,SA رابطه های مهم: مخروط : (cone) مخروط به معنی خراشیده شده ، تراشیده شده و خراطی شده است ودر اصطلاح هندسه حجمی است که از دوران مثلث قائم الزاویه حول یک ضلع آن به دست می آید . کله قند و کلاه بوقی ...
فرمول محاسبه حجم اشکال هندسی

فرمول های ریاضی(محیط،مساحت و حجم اشکال هندسی) یک ضلع × خودش = مساحت مربع یک ضلع × ۴ = محیط مربع طول × عرض = مساحت مستطیل ۲× (طول + عرض) = محیط مستطیل ۲ ÷ (قاعده × ارتفاع) = مساحت مثلث مجموع سه ضلع = محیط مثلث نصف ارتفاع × (قاعده بزرگ + قاعده کوچک) = مساحت ذوزنقه مجموع ۴ ضلع = محیط ذوزنقه ۲÷ (قطر بزرگ × قطر کوچک) = مساحت لوزی یک ضلع × ۴ = محیط لوزی ارتفاع × قاعده = مساحت متوازی الاضلاع مجموع دو ضلع متوالی × ۲ = محیط متوازی الاضلاع عدد پی × مجذور شعاع = مساحت دایره ۱۴/۳ × شعاع × شعاع ۱۴/۳ × قطر = محیط دایره مساحت کره چهار ×عدد پی × مجذور شعاع = مساحت کره حجم کره عدد پی × شعاع به توان ۳ = حجم کره ۱۴/۳ × (نصف قطر کوچک × نصف قطر بزرگ) = مساحت بیضی یک ضلع × تعداد اضلاع = محیط چند ضلعی منتظم طول یال × مساحت یک وجه = حجم مکعب ارتفاع × عرض × طول = حجم مکعب مستطیل ارتفاع × قاعده = حجم مکعب ارتفاع هرم × مساحت قاعده هرم = حجم هرم ارتفاع × مساحت قاعده = حجم استوانه ارتفاع × محیط قاعده = مساحت جانبی سطح دو قاعده + مساحت جانبی = سطح کل استوانه مجموع مساحت سطوح جانبی = مساحت جانبی منشور مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی = مساحت کلی منشور ارتفاع × مساحت قاعده = حجم مخروط
مساحت ها ، محیط ها و حجم اشکال هندسی
۱) مساحت مـــربع = یـــک ضلع × خـــودش محیــط مـــربــــع = یک ضلع × ۴۲) مساحت مسـتطیـــــــل = طـول × عـرض محیط مستطیل = ( طول + عرض) × ۲۳) مساحت مثلث = ( قاعده × ارتــــــفاع ) ÷ ۲ محیط مثلث = مجموع سه ضلع۴) مساحت مثلث متساوی الاضلاع = ( قاعده × ارتفاع ) ÷ ۲ محیط مثلث متساوی الاضلاع = یک ضلع × ۳۵) مساحت مثلث متساوی الساقین = ( قاعده × ارتفاع ) ÷ ۲ محیط مثلث متساوی الساقین= مجموع سه ضلع۶) مساحت مثلث قائم الزاویه = ( قاعده × ارتفاع ) ÷ ۲ محیط مثلث قائم الزاویه = مجموع سه ضلع۷) مساحت ذوزنقه = ( قاعده بزرگ + قاعده کوچک ) × نصف ارتفاع محیط ذوزنقه = مجموع چهار ضلع۸) مساحت لوزی = ( قطر بزرگ × قطر کوچک ) ÷ ۲ محیط لوزی = یک ضلع × ۴۹) مساحت متوازی الاضلاع = قاعده × ارتفاع محیط متوازی الاضلاع = مجموع دو ضلع متوالی × ۲۱۰) مساحت دایره = عدد پی (3/14 ) × شعاع × شعاع محیط دایره = عدد پی ( 3/14 ) × قطر۱۱) مساحت کره = ۴ ×3/14 × شعاع به توان دو حجم کره = چهار سوم × 3/14 × شعاع به توان سه۱۲) مساحت بیضی = (نصف قطر بزرگ × نصف قطر کوچک ) ×3/14 ۱۳ ) محیط چند ضلعی منتظم = یک ضلع × تعداد اضلاعش۱۴ ) حجم مکعب مستطیل = طـول × عـرض × ارتفاع حجم مکعب مربع = قاعده × ارتفاع ( طول یال×مساحت یک وجه)۱۵ ) حجم هرم = مساحت قاعده ی هرم × ارتفاع هرم× یک سوم 16) مساحت جانبی استوانه = محیط قاعده × ارتفاع حجم استوانه = مساحتقاعده × ارتفاعسطح کل استوانه = سطح دو قاعده + مساحت جانبی ( مساحت مجموع دو قاعده + ارتفاع × پیرامون قاعده )۱۷) مساحت جانبی منشور = مجموع مساحت سطوح جانبی مساحت کلی منشور = مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی۱۸) حجم مخروط = مساحت قاعده × یک سوم × ارتفاع
مساحت ، محیط و حجم شکلهای هندسی
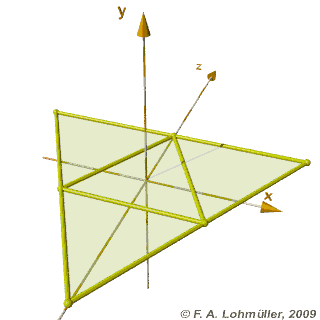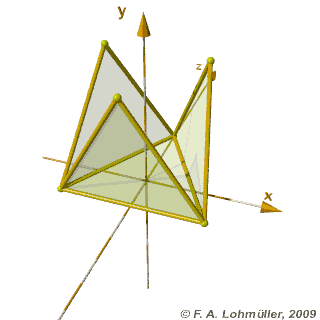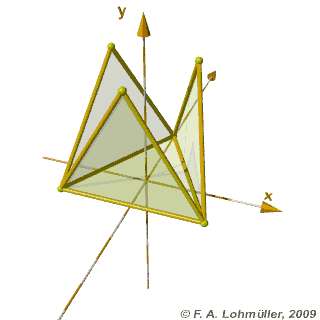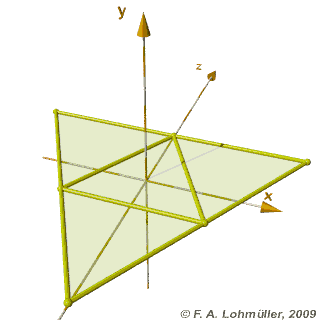
مساحت مثلث با معلوم بودن سه ضلع آن برابرحاصل جذر (( p× ( p -a) × (p - b) × (p-c ) است که در آن p نصف محیط مثلث است وa,b,c ضلعهای مثلث هستند. مساحت مثلث برابراست با: نصف حاصلضرب يك قاعده در ارتفاع نظيرش مساحت متوازی الاضلاع برابر است با: حاصلضرب يك قاعده در ارتفاع مساحت مستطیل برابر است با : طول × عرض مساحت لوزی برابر است با : نصف حاصلضرب دو قطر مساحت مربع برابراست با : حاصلضرب یک ضلع در خودش ( يا مجذور يك ضلع ) مساحت ذوزنقه برابر است با: 2÷ ( حاصل جمع دو قاعده × ارتفاع ) محیط چندضلعی ها بالا برابر است حاصل جمع اندازه ی ضلع های آنها مساحت دایره برابر است با : شعاع× شعاع × ۱۴/۳ محیط دایره برابر است با : قطر × ۱۴/۳ مساحت بیضی برابر است با : نصف قطر بزرگ × نصف قطر کوچک × ۱۴/۳ مساحت کره برابر : شعاع × شعاع × ۱۴/۳× 4 حجم کره برابر : 3 ÷ ( شعاع × شعاع × شعاع × ۱۴/۳× 4 ) حجم استوانه برابر است با : مساحت قاعده × ارتفاع یعنی ( شعاع × شعاع × ارتفاع × ۱۴/۳ ) مساحت بدنه ( سطح جانبی )استوانه برابر : ارتفاع× ۱۴/۳× قطر حجم منشور برابراست با: مساحت قاعده × ارتفاع مساحت بدنه ( سطح جانبی ) منشور برابر :محیطقاعده× ارتفاع حجم هرم برابر است با: 3 ÷(مساحت قاعده × ارتفاع ) حجم مخروط برابر است با: 3÷ (مساحت قاعده × ارتفاع ) حجم مکعب مستطیل برابر : طول× عرض× ارتفاع
حجم ومساحت اشکال هندسی /ریاضی ششم
حجم: حجم در لغت به معنی برآمدگی و ستبری و جسامت چیزی می باشد و در اصطلاح هندسه گنجایش و ظرفیت جسم و آن مقداری از فضا که جسم آن را اشغال می کند, را نشان می دهد. منشور: منشور در لغت به معنی پراکنده, نشر شده, زنده شده و مبعوث است و در اصطلاح هندسه نام شکلی است که دو قاعده دارد که دو چند ضلعی مساوی هستند و بدنه منشور(سطح جانبی منشور ) از مستطیلها یا متوازی الاضلاع ها تشکیل شده است. معرفی منشور 5 پهلو: í نام شکل: منشور 5 پهلو í یال های منشور: 'EE',DD',CC',BB',AA í وجه منشور: هر کدام از مستطیل های جانبی را یک وجه منشور می نامند. í ارتفاع منشور: از آنجا که هر کدام از یال ها بر دو قاعده منشور عمود می باشند, لذا ارتفاع منشور با اندازه هر یک از یال ها برابر است. í قاعده ی منشور: منشور دو قاعده دارد. ABCDE و 'A'B'C'D'E که دو پنج ضلعی مساوی اند. رابطه های مهم: ارتفاع × مساحت قاعده = حجم منشور ارتفاع × محیط قاعده = مساحت جانبی منشور مساحت دو قاعده + مساحت جانبی = مساحت کل منشور استوانه: (Cylinder) نام شکلی است که دو قاعده دارد که دو دایره مساوی هستند و بر جانبی راست استوار است. اگر مستطیل را حول طول آن دوران دهیم, شکل فضایی حاصل استوانه نامیده می شود. در این صورت طول مستطیل ارتفاع استوانه و عرض آن شعاع قاعده استوانه می باشد. در شکل بالا مستطیل ABCD را حول طول آن دوران داده ایم و استوانه بوجود آمده است. رابطه های مهم: ارتفاع×مساحت قاعده(دایره) = حجم استوانه ارتفاع×محیط قاعده(دایره) = مساحت جانبی استوانه مساحت دو قاعده + مساحت جانبی = مساحت کل استوانه
مساحت ومحيط اشكال هندسي
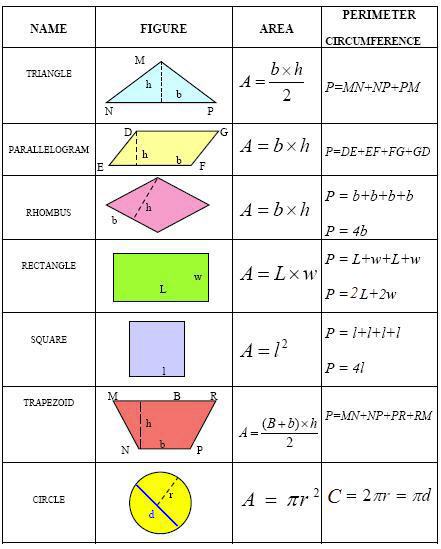
محیط و مساحت فرمول های ریاضی(محیط،مساحت و حجم اشکال هندسی) یک ضلع × خودش = مساحت مربع یک ضلع × 4 = محیط مربع طول × عرض = مساحت مستطیل 2× (طول + عرض) = محیط مستطیل 2 ÷ (قاعده × ارتفاع) = مساحت مثلث مجموع سه ضلع = محیط مثلث نصف ارتفاع × (قاعده بزرگ + قاعده کوچک) = مساحت ذوزنقه مجموع 4 ضلع = محیط ذوزنقه 2÷ (قطر بزرگ × قطر کوچک) = مساحت لوزی یک ضلع × 4 = محیط لوزی ارتفاع × قاعده = مساحت متوازی الاضلاع مجموع دو ضلع متوالی × 2 = محیط متوازی الاضلاع عدد پی × مجذور شعاع = مساحت دایره 14/3 × شعاع × شعاع 14/3 × قطر = محیط دایره مساحت کره چهار ×عدد پی × مجذور شعاع = مساحت کره حجم کره عدد پی × شعاع به توان 3 ضرب در عدد چهار سوم = حجم کره 14/3 × (نصف قطر کوچک × نصف قطر بزرگ) = مساحت بیضی یک ضلع × تعداد اضلاع = محیط چند ضلعی منتظم طول یال × مساحت یک وجه = حجم مکعب ارتفاع × عرض × طول = حجم مکعب مستطیل ارتفاع × قاعده = حجم مکعب ارتفاع هرم × مساحت قاعده هرم بر روي سه= حجم هرم ارتفاع × مساحت قاعده = حجم استوانه ارتفاع × محیط قاعده = مساحت جانبی سطح دو قاعده + مساحت جانبی = سطح کل استوانه مجموع مساحت سطوح جانبی = مساحت جانبی منشور مجموع مساحت دو قاعده + مجموع مساحت سطوح جانبی = مساحت کلی منشور ارتفاع × مساحت قاعده برروي سه= حجم مخروط محیط - مساحت - محیط و مساحت اشکال هندسی مساحت مـــربع = اندازه يـــک ضلع × ضلع دیگر محيــط مـــربــــع = يک ضلع × 42) مساحت مسـتطيـــــــل = طـول × عـرض محيط مستطيل = ( طول + عرض) × 23) مساحت مثلث = ( قاعده × ارتــــــفاع ) ÷ 2 محيط مثلث = مجموع سه ضلع4) مساحت مثلث متساوي الاضلاع = ( قاعده × ارتفاع ) ÷ 2 محيط مثلث متساوي الاضلاع = يک ضلع × 3 5) مساحت مثلث متساوي الساقين = ( قاعده × ارتفاع ) ÷ 2 محيط مثلث متساوي الساقين= مجموع سه ضلع 6) مساحت مثلث قائم الزاويه = ( قاعده × ارتفاع ) ÷ 2 محيط مثلث قائم الزاويه = مجموع سه ضلع 7) مساحت ذوزنقه = ( قاعده بزرگ + قاعده کوچک ) × نصف ارتفاع محيط ذوزنقه = مجموع چهار ضلع 8) مساحت لوزي = ( قطر بزرگ × قطر کوچک ) ÷ 2 محيط لوزي = يک ضلع × 4 9) مساحت متوازي الاضلاع = قاعده × ارتفاع محيط متوازي الاضلاع = مجموع دو ضلع متوالي × 2 10) مساحت دايره = عدد پي ( 14/3 ) × شعاع × شعاع محيط دايره = عدد پي ( 14/3 ) × قطر 11) مساحت کره = 4 × 14/3 × شعاع به توان دو حجم کره = چهار سوم × 14/3 × شعاع به توان سه 12) مساحت بيضي = (نصف قطر بزرگ × نصف قطر کوچک ) × 14/3 13 ) محيط چند ضلعي منتظم = يک ضلع × تعداد اضلاعش 14 ) حجم مکعب مستطيل = طـول × عـرض × ارتفاع حجم مکعب مربع = قاعده × ارتفاع ( طول يال×مساحت يک وجه) 15 ) حجم هرم = مساحت قاعده ي هرم × ارتفاع ...
حجم ومساحت اشکال هندسی /ریاضی ششم
دانش آموزان عزیز :در ایام تعطیلات نوروز با مطالعه و تمرین بخش مساحت و حجم به اطلاعات خود در این زمینه بیفزایید حجم:(Volume) حجم در لغت به معنی برآمدگی و ستبری و جسامت چیزی می باشد و در اصطلاح هندسه گنجایش و ظرفیت جسم و آن مقداری از فضا که جسم آن را اشغال می کند, را نشان می دهد. منشور: (Prism) منشور در لغت به معنی پراکنده, نشر شده, زنده شده و مبعوث است و در اصطلاح هندسه نام شکلی است که دو قاعده دارد که دو چند ضلعی مساوی هستند و بدنه منشور(سطح جانبی منشور ) از مستطیلها یا متوازی الاضلاع ها تشکیل شده است. معرفی منشور 5 پهلو: í نام شکل: منشور 5 پهلو í یال های منشور: 'EE',DD',CC',BB',AA í وجه منشور: هر کدام از مستطیل های جانبی را یک وجه منشور می نامند. í ارتفاع منشور: از آنجا که هر کدام از یال ها بر دو قاعده منشور عمود می باشند, لذا ارتفاع منشور با اندازه هر یک از یال ها برابر است. í قاعده ی منشور: منشور دو قاعده دارد. ABCDE و 'A'B'C'D'E که دو پنج ضلعی مساوی اند. رابطه های مهم: ارتفاع × مساحت قاعده = حجم منشور ارتفاع × محیط قاعده = مساحت جانبی منشور مساحت دو قاعده + مساحت جانبی = مساحت کل منشور استوانه: (Cylinder) نام شکلی است که دو قاعده دارد که دو دایره مساوی هستند و بر جانبی راست استوار است. اگر مستطیل را حول طول آن دوران دهیم, شکل فضایی حاصل استوانه نامیده می شود. در این صورت طول مستطیل ارتفاع استوانه و عرض آن شعاع قاعده استوانه می باشد. در شکل بالا مستطیل ABCD را حول طول آن دوران داده ایم و استوانه بوجود آمده است. رابطه های مهم: ارتفاع×مساحت قاعده(دایره) = حجم استوانه ارتفاع×محیط قاعده(دایره) = مساحت جانبی استوانه مساحت دو قاعده + مساحت جانبی = مساحت کل استوانه هرم: (pyramid) هرم در لغت به معنی سخت پیر گردیدن و کلان سال شدن است و در اصطلاح هندسه حجمی است که قاعده آن یک چند ضلعی و وجوه جانبی اش مثلثهایی باشند که همه به یک رأس مشترک(رأس هرم) منتهی می شوند. معرفی هرم منتظم: í نام شکل: هرم منتظم. í رأس هرم: نقطه S í ارتفاع هرم: پاره خطی است که از رأس هرم به مرکز قاعده ی هرم عمود است(SO) í قاعده هرم: پنج ضلعی منتظم ABCDE í سهم هرم: ارتفاع مثلث های جانبی, ارتفاع هر وجه جانبی هرم منتظم(SH). í وجه هرم: هر یک از مثلث هایی که بدنه هرم را می پوشانند را یک وجه جانبی می نامیم. í یال هرم: محل تقاطع هر دو وجه جانبی را یال هرم می نامیم. SE,SD,SC,SB,SA رابطه های مهم: مخروط : (cone) مخروط به معنی خراشیده شده ، تراشیده شده و خراطی شده است ودر اصطلاح هندسه حجمی است که از دوران مثلث قائم الزاویه حول یک ضلع آن به دست می آید . کله قند و کلاه ...
محاسبه محیط + مساحت + حجم اشکال هندسی

نرم افزار ترسیم اشکال هندسی GeoGebra v4.0.27 نرم افزار Geogebra محصول تیم متخصص با پشتیبانی دانشگاه سالزبورگ اتریش و سرپرستی مارکوس هوهن وارتر است که برای ترسیم اشکال هندسی به کار میرود. نرم افزار پوشش نسبتاً جامعی به مباحث حساب، جبر و هندسه فراهم کرده است. در برنامه محیط ترسیم اشکال هندسی، محیط ورود فرمان های ریاضی و ناحیه اطلاعات جبری در نظر گرفته شده است. خروجی جاوا اپلت این نرم افزار بدون نقص به همراه گزینه های فراوانی است که طراح آموزشی را قادر به تولید طرح درس های تعاملی با کیفیت بالا می کند. نرم افزار GeoGebra در مقایسه با دیگر نرم افزارها از لحاظ توانمندی های ترسیمی، ظاهر، وسعت عمل، محتوای آموزشی برای معلمین و دانش آموزان، ارتباط با کاربران، خروجی جاوا و بروز بودن مناسب ترین نرم افزار محسوب می شود.مطلب و نرم افزار فوق از سایت پی سی دانلوداستخراج گردیده است
مساحت ، محیط و حجم شکل های هندسی
مساحت مثلث با معلوم بودن سه ضلع آن برابرحاصل جذر p× (p-a) × (p-b) × (p-c)است که در آن p نصف محیط مثلث است وa,b,c ضلعهای مثلث هستند. مساحت مثلث برابراست با: نصف حاصلضرب قاعده در ارتفاع مساحت متوازی الاضلاع برابر است با: حاصلضرب قاعده در ارتفاع مساحت مستطیل برابر است با : طول × عرض مساحت لوزی برابر است با : نصف حاصلضرب دو قطر مساحت مربع برابراست با : حاصلضرب یک ضلع در خودش مساحت ذوزنقه برابر است با: 2÷ ( حاصل جمع دو قاعده × ارتفاع ) محیط چندضلعی ها بالا برابر است حاصل جمع اندازه ی ضلع های آنها مساحت دایره برابر است با : شعاع× شعاع × 14/3 محیط دایره برابر است با : قطر × 14/3 مساحت بیضی برابر است با : نصف قطر بزرگ × نصف قطر کوچک × 14/3 مساحت کره برابر : شعاع × شعاع × 14/3× 4 حجم کره برابر : 3 ÷ ( شعاع × شعاع × شعاع × 14/3× 4 ) حجم استوانه برابر است با : مساحت قاعده × ارتفاع یعنی ( شعاع × شعاع × ارتفاع × 14/3 ) مساحت بدنه ( سطح جانبی )استوانه برابر : ارتفاع× 14/3× قطر حجم منشور برابراست با: مساحت قاعده × ارتفاع مساحت بدنه ( سطح جانبی ) منشور برابر :محیطقاعده× ارتفاع حجم هرم برابر است با: 3 ÷(مساحت قاعده × ارتفاع ) حجم مخروط برابر است با: 3÷ (مساحت قاعده × ارتفاع ) حجم مکعب مستطیل برابر : طول× عرض× ارتفاع فرمول های ریاضی یک ضلع × خودش = مساحت مربع یک ضلع × 4 = محیط مربع طول × عرض = مساحت مستطیل 2× (طول + عرض) = محیط مستطیل 2 ÷ (قاعده × ارتفاع) = مساحت مثلث مجموع سه ضلع = محیط مثلث نصف ارتفاع × (قاعده بزرگ + قاعده کوچک) = مساحت ذوزنقه مجموع 4 ضلع = محیط ذوزنقه 2÷ (قطر بزرگ × قطر کوچک) = مساحت لوزی یک ضلع × 4 = محیط لوزی ارتفاع × قاعده = مساحت متوازی الاضلاع مجموع دو ضلع متوالی × 2 = محیط متوازی الاضلاع عدد پی × مجذور شعاع = مساحت دایره 14/3 × شعاع × شعاع 14/3 × قطر = محیط دایره مساحت کره چهار ×عدد پی × مجذور شعاع = مساحت کره حجم کره عدد پی × شعاع به توان 3 = حجم کره 14/3 × (نصف قطر کوچک × نصف قطر بزرگ) = مساحت بیضی یک ضلع × تعداد اضلاع = محیط چند ضلعی منتظم طول یال × مساحت یک وجه = حجم مکعب ارتفاع × عرض × طول = حجم مکعب مستطیل ارتفاع × قاعده = حجم مکعب ارتفاع هرم × مساحت قاعده هرم = حجم هرم ارتفاع × مساحت قاعده = حجم استوانه ارتفاع × محیط قاعده = مساحت جانبی سطح دو قاعده + مساحت جانبی = سطح کل استوانه مجموع ...
