جدول توابع مثلثاتی
جدول مقادير توابع مثلثاتي
لينك كمكي دانلود
جدول انتگرال توابع
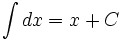
جدول انتگرال توابع گویا جدول انتگرال توابع گنگ توجه داشته باشید که : جدول انتگرال توابع نمایی: بطوریکه: جدول انتگرال توابع مثلثاتی انتگرال توابع مثلثاتی شامل sin انتگرال توابع مثلثاتی شامل cos انتگرال توابع مثلثاتی شامل tan انتگرال توابع مثلثاتی شامل cot انتگرال توابع مثلثاتی شامل sec انتگرال توابع مثلثاتی شامل csc انتگرال توابع مثلثاتی شامل sin , cos انتگرال توابع مثلثاتی شامل sin , tan انتگرال توابع مثلثاتی شامل cos ,tan انتگرال توابع مثلثاتی شامل sin , cot انتگرال توابع مثلثاتی شامل cos ,cot انتگرال توابع مثلثاتی شامل tan , cotهمچنین ببینید جدول انتگرال توابع مثلثاتی انتگرال توابع مثلثاتی شامل sin where cvs{x} is the [Coversine]] function انتگرال توابع مثلثاتی شامل cos انتگرال توابع مثلثاتی شامل tan انتگرال توابع مثلثاتی شامل cot انتگرال توابع مثلثاتی شامل sec انتگرال توابع مثلثاتی شامل csc انتگرال توابع مثلثاتی شامل sin , cos همچنین: همچنین: همچنین: همچنین: همچنین: انتگرال توابع مثلثاتی شامل sin , tan
توابع مثلثاتی
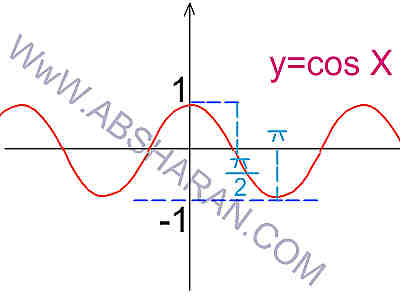
تابع مثلثاتی Cos نیز یکی از توابع مهم مثلثاتی است.همانطور که از نمودارد تابع مثلثاتی Cos پیداست,این تابع یک تابع زوج است (نسبت به محور Y قرینه است).دامنه ی تابع مثلثاتی Cos مجوعه ی اعداد حقیقی و برد این تابع مثلثاتی اعداد بین 1 و 1- می باشند.یعنی مقدار از 1 بیشتر و از 1- کمتر نمی شود.نمودار تابع Cos بصورت زیر است: با توجه به نمودار تابع مثلثاتی Cos این تابع نیز یک به یک نمی باشد.از آنجاییکه تابع Cos یک تابع زوج است پس رابطه ی زیر برقرار می باشد: آموزش مثلثات,تابع مثلثاتی سینوس Sin یکی از توابع پرکاربرد مثلثاتی است.همانطور که از نمودار تابع مثلثاتی سینوس پیداست,این تابع یک تابع فرد است (نسبت به مبداء مختصات قرینه است).دامنه ی تابع مثلثاتی سینوس sin مجوعه ی اعداد حقیقی و برد این تابع مثلثاتی اعداد بین 1 و 1- می باشند.یعنی مقدار سینوس از 1 بیشتر و از 1- کمتر نمی شود.نمودار تابع Sin سینوس بصورت زیر است: با توجه به نمودار تابع مثلثاتی سینوس Sin این تابع یک به یک نیز نمی باشد.از آنجاییکه تابع سینوس یک تابع فرد است پس رابطه ی زیر برقرار می باشد: Y=Sin(-X)=-SinX آموزش مثلثاتدر ابتدای آموزش مثلثات به بررسی دایره ی مثلثاتی می پردازیم,دایره ی مثلثاتی شما را در یافتن مقادیر زاویه ها در مثلثات یاری می کند.: هر دایره دارای یک مبداء بوده که شروع حرکت متحرک از آن جا آغاز می گردد,دارای 4 ناحیه می باشد,دارای جهت اصلی خلاف عقربه های ساعت (جهت مثبت) می باشد.دارای 4 محور است که محور سینوس Sin و تانژانت tg موازی هم و محور Cos و کتانژانت Cotg در دایره ی مثلثاتی موازی هم هستند. تغییرات sin و cos بین 1 و 1- و تغییرات تانژانت tg و cotg از تا است. روش محاسبه ی نسبت های مثلثاتی: برای محاسبه ی sin و cos یک زاویه انتهای کمان را بر محور Sin و یا cos عمود می کنیم,ولی برای محاسبه ی tg و یا cotg یک زاویه انتهای کمان را امتداد داده تا محور tg و یا cotg را قطع کند. اگر x زاویه ای در ناحیه ی اول باشد,در ناحیه ی اول تمام نسبت های مثلثاتی مثبت است. اگر x در ناحیه ی دوم باشد فقط سینوس sin مثبت است. اگر x در ناحیه ی سوم باشد در ناحیه ی سوم سینوس sin و cos منفی و تانژانت tg و کتانژانت cotg مثبت است. اگر x در ناحیه ی چهارم باشد,در ناحیه ی چهارم فقط cos مثبت است. ده رابطه ی مهم مثلثاتی: ================================================================================================ نسبت های مثلثاتی کمان 2x : ============================================================================= نسبت های مثلثاتی زوایای 3x : ================================================================================================= نکته: ==================================================================================================== چند نسبت دیگر: ================================================================================================== فرمول ...
جدول توابع مثلثاتی
درستی جدول بالا را تحقیق کنید.
دانلود جزوه توابع مثلثاتی
کلیک کنید برای دانلودClick Me Text
خلاصه تبدیل لاپلاس و مباحث وابسته
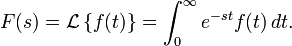
تعریف ریاضی تبدیل لاپلاسلازم به ذکر است که این تبدیل یک تابع را از فضای حقیقی (متغیر t) به فضای مختلط (متغیر s) میبرد.در زیر تبدیل لاپلاس های معروف و همچنین پرکاربردترین ویژگی های تبدیل لاپلاس را ارائه میدهم.تذکر1:منظور از (Dirac(t,n مشتق nام تابع ضربه یا همان دیراک(دلتا) است که در نتیجه n=0 همان تابع ضربه است.تذکر2:تمامی توابع خطی چند جمله ای از عبارت دومی ساخته میشوند مثلاً تابع پله(هوی ساید) همان n=0 است.دانلود جدول تبدیل لاپلاسفرمولهای عمومیتوابع توانیتوابع نماییتوابع هیپربولیکتوابع لگاریتمیتوابع مثلثاتیتوابع خطاتوابع بسل
فرمولهای مشتق و انتگرال
مشتق توابع (قالب pdf) توضیحات: در این جدول، قوانین کلی مشتق گیری و نیز فرمولهای مشتق توابع نمایی و لگاریتمی،توابع مثلثاتی و معکوس مثلثاتی و مشتق توابع هذلولوی و معکوس هذلولوی را مشاهده خواهید کرد. این جدول شامل ۳۶ فرمول مختلف است. جدول بزرگ انتگرالهای توابع (فالب pdf) توضیحات: این جدول شامل ۱۲۰ انتگرال مختلف در ۱۰ فرم متفاوت از توابع است. حل معادلات درجه اول تا چهارم توضیحات: با کلیک بر عبارت بالا وارد سایتی خواهید شد که در آن مقالات کوتاه متعددی درباره حلمعادلات درجه اول تا چهارم و معادلات خطی دیگر گنجانده شده است. منبع : دانلود کتاب مهندسی الکترونیک مهندسی عمران
جدول نسبت های مثلثاتی
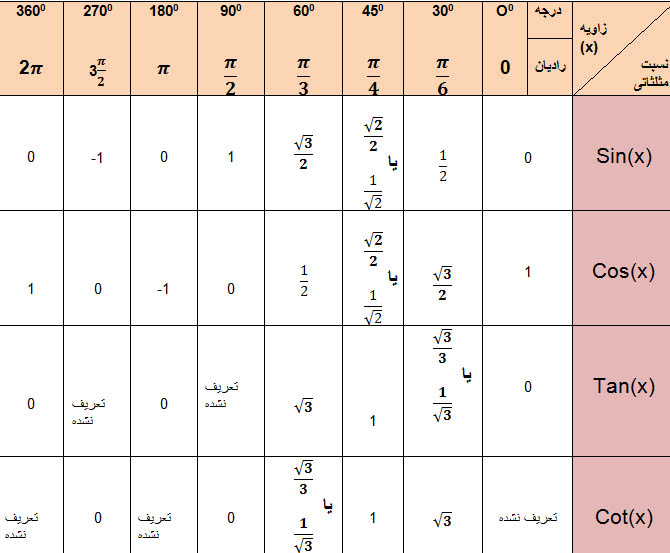
بنا به درخواست دوستان در این بخش جدول نسبت های مثلثاتی رو میذارم به امید حفظ شدن این جدول برای شما که هیچوقت نتونستم به خاطر بسپارمش!! همچنین امکان دانلود کردن جدول در زیر عکس فراهم شده download
تاریخچه ی توابع مثلثاتی
مثلثات از درون هندسه در آمد و بیش از همه،ریاضیدانان ایرانی روی آن کار کردند.بررسی های اخترشناسی در بابل قدیم و یونان، ریاضیدانان را به سمت موضوع هایی کشانید که می توان آن را پیش درآمد مثلثات دانست."آریستارک" و "اراتستن" دو دانشمند مقیم اسکندریه در سده سوم پیش از میلاد،از مفهوم های نخستین مثلثات یاری می جستند.ارشمیدس-دانشمند بزرگ یونانی-(287 تا 212 پیش از میلاد)،ضمن بررسی هایی درباره ی دایره،برای محاسبه ی وترها و یافتن دستورهایی برای جمع و تفریق کمان ها،تلاش هایی کرد."هیپارک" اخترشناس یونانی میانه های سده دوم میلادی،تقسیم دایره را به شیوه بابلی ها پذیرفت و جدولی تنظیم کرد که در آن برخی وترها از روی کمان آن ها محاسبه شده بود."منلائوس"و"بطلمیوس"در سده ی دوم میلادی هم،کارهایی در این زمینه دارند ولی دانشمندان یونانی که به ویژه روی هندسه کار می کردند،وتر کمان ها را به کار می بردند و نتوانستند به خطهای مثلثاتی دست یابند.در واقع نخستین تابع های مثلثاتی را باید جدول وترها بر حسب کمان آن ها دانست که برای محاسبه های اخترشناسی لازم بود و در دو سده ی پیش از میلاد به وجود آمد.برای نخستین بار دانشمندان هندی در فاصله زمانی از سده پنجم تا دوازدهم میلادی از "نیم وتر" به جای وتر استفاده می کردند که متناظر با مفهوم سینوس امروزی است.آن ها نیم وتر را "اردهاجیا"(یا"جیا اردها") می گفتند که از لحاظ لغوی به معنای نصف وتر است.به تدریج اردهاجیا را کوتاه کردند و "جیا" نامیدند.به جز این،هندی ها از یک منهای کسینوسx هم استفاده می کردند و آن را "کوماجیا" می نامیدند و مقدار cosx را "کوتی جیا" می گفتند."ابوالوفای بوزجانی"(940 تا 988 میلادی)ریاضیدان ایرانی(ویرانه های بوزجان نزدیک تربت جام است)،تانژانت را به نام "ظل" وارد مثلثات کرد و جدولی را تنظیم کرد که 30دقیقه به 30دقیقه مقدار سینوس ها را تعیین می کرد.دستورهای sin a+b و sin a-b را کشف کرد و برخی از مساله های مثلثات کروی را حل نمود.اما گام اصلی را نصیرالدین طوسی برداشت.تالیف او به نام"کشف القناع فی اسرار شکل القطاع"در واقع نخستین کتاب درباره مثلثات است.نقش طوسی را در مثلثات،باید شبیه نقش اقلیدس در هندسه دانست..زیرا او توانست مجموعه ی آن چه را که پیش از او وجود داشت،به صورت دانشی مستقل و منظم درآورد.ترجمه ای از کتاب طوسی در سال 1891 به زبان فرانسوی انجام گرفت و تا مدت ها به عنوان کتاب درسی،مورد استفاده ی دانش پژوهان در اروپای غربی بود.سینوس را به زبان عربی"جَیب"به معنای"گریبان"می گفتند که به همان معنا به زبان فرانسوی برگردانده شد."سینوس" یعنی گریبان.به همین مناسبت،برخی معتقدند که خوارزمی یا هم عصران او،"سینوس" ...
