توابع مختلط
توابع مخطلط

توابع مختلط درس توابع مختلط شامل موضوعات زیر است: ۱- مباحث پایه ای در نظریه توابع تحلیلی یک متغیره، و مختصری از توابع تحلیلی چند متغیره، ۲- اعداد مختلط و سری های توانی فرمال۳- توابع مختلط، معادلات کوشی-ریمان، انتگرال مختلط، فرمول انتگرال کوشی، باقیمانده ها۴- توابع هارمونیک و نگاشت کانفورمال و قضیه ی نگاشت ریمانپیش نیاز های این درس شامل ریاضی عمومی ۲، آنالیز ریاضی ۱ و توپولوژی است. منبع درس کتاب : Elementary theory of analytic functions with one and several variables از Henri Cartan مجموعه: دانشگاه صنعتی شریف تعداد ویدئو ها : 47 ویدئو درباره آموزگار: امیر جعفریامیر جعفری استادیار دانشکده ی علوم ریاضی دانشگاه صنعتی شریف است. وی دکتری خود را در سال ۲۰۰۳ میلادی از دانشگاه بران (Brown) در امریکا دریافت کرده است. زمینه ی پژوهش دکتر جعفری هندسه ی جبری و نظریه اعداد است. وی در سال های اخیر درس هایی را در زمینه های مختلف ریاضی در دانشگاه شریف ارائه کرده است.
انواع تابع
یک همسایگی باشد. تعاریف تابع هر هیچ نقطه از دامنه خود پیوسته نمیباشد. تابع تحلیلی تابع تحلیلی، تابعی است که به طور محلی به وسیله یک سری توانی همگرا مشخص می شود. می توان به توایع تحلیلی مانند یک پل بین چند جمله ایها و توابع در حالت کلی فکر کرد. اینجا توابع تحلیلی حقیقی و توابع تحلیلی مختلط وجود دارند، که شباهتها و تفاوتهایی دارند. یک تابع تحلیلی است اگر برابر با سری تیلورش در تابع f رو مجموعهٔ باز D در خط حقیقی، تحلیلی حقیقی است اگر برای هر x0 در D بتوان نوشت: در این فرمول ضرایب a0, a1, ... اعداد حقیقی هستند و سری برای x در یک همسایگی از x0 همگرا است. به صورت دیگر، یک تابع تحلیلی یک تابع بینهایت بار مشتق پذیراست به این صورت که سری تیلور در هر نقطه x0 در دامنه اش برای x به اندازه کافی نزدیک به x0 همگراست و مقدارش برابر با f(x) است. تعریف یک تابع تحلیلی مختلط با جایگزین کردن «مختلط» به جای «حقیقی» و «صفحهٔ مختلط» به جای «خط حقیقی» در مطالب بالا بدست می آید. مثال ها هر چند جملهای (حقیقی یا مختلط) یک تایع تحلیلی است. به این دلیل که اگر یک چند جمله ای از درجه n باشد، هر جمله ازدرجه بزرگتر از n در بسط سری تیلورش صفر است، وبنا براین، این سری به طور جزئی همگرا خواهد بود. تابع نمایی تحلیلی است. هر سری تیلور برای این تابع نه فقط برای x به اندازه کافی نزدیک به x0 (همان طور که در تعریف آمده) بلکه برای همه مقدار x (حقیقی یا مختلط) همگرا می شود. توابع مثلثاتی، لگاریتم و توابع توانی روی هر بازهٔ باز در دامنهٔشان تحلیلی اند. تابع قدر مطلق تحلیلی نیست زیرا مشتق پذیر نیست. توابع تعریف شدهٔ تکه ای(تابعهای معلوم به وسیله فرمولهای مختلف در مناطق مختلف) تحلیلی نیستند. خصوصیات توابع تحلیلی مجموع ها، ضرب ها و ترکیبات توابع تحلیلی، تحلیلی اند. · معکوس یک تابع تحلیلی که هیچ کجا صفر نیست، تحلیلی است. هر تابع تحلیلی هموار است. یک چند جمله ای نمیتواند در تعداد زیادی نقطه صفر باشد مگر اینکه چند جمله ای صفر باشد (به طور دقیق تر، تعداد صفرها حداکثر می تواند به اندازهٔ درجهٔ چندجمله ای باشد). حکمی مشابه ولی ضعیفتر برای توابع تحلیلی وجود دارد. اگر مجموعهٔ صفرهای تابع تحلیلی f یک نقطهٔ انباشتگی در دامنه اش داشته باشد، آنگاه f در تمام مؤلفهٔ همبندی که شامل نقطهٔ انباشتگیست صفر است. تابع هولومورفیک توابع هولومورفیک موضوع اصلی در مطالعهٔ آنالیز مختلط هستند. آنها توابعی هستند که بر روی یک زیر مجموعهٔ باز از صفحهٔ مختلط C تعریف شده اند با مقادیری در C که در هر نقطه مشتق مختلط دارند. iهولومورفيك بودن یک شرط قویتر از مشتقپذیری مختلط است و دلالت ...
اعداد مختلط
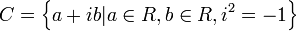
عدد مختلط مقدمه اعداد مختلط هنوز هم درنظر برخی با شک آمیخته با ترس همراه است. ولی درنظر ریاضیدانان امروزی این دستگاه صرفا گسترش مجموعه بنیاد سادهای از اعداد حقیقی است. همیلتون (Hamilton) ریاضیدان قرن نوزدهم گسترشی برای اعداد مختلط پیدا کرد و آن را چهارگانها نامید. ماهیت ریاضیات جدید چنان است که باید دید خود را وسیعتر کنیم و به دستگاههایی اصل موضوعی بپردازیم که بافتهای ریاضی مفیدتری را بدست دهند. مفهوم عدد چیزی جز قسمتی از این برای کلی نیست. جبر جدید یا دستگاههایی اصل موضوعی سروکار دارد که ، بطور کلی متشکل از مجموعههایی است همراه با عملهای مختلفی روی آن مجموعهها. دوتا از این دستگاهها عبارتند از حلقه و میدان. اگر بخواهیم پا را از اعداد مختلط فراتر نهیم، مسیر پربار راه چهارگانهای همیلتون نیست بلکه مسیر ساختهای جبری تقسیم یافته جبر جدید است. عدد مختلط عددی به شکل است که aو bاعداد حقیقیاند و iیکهٔ موهومی با خصوصیت i2 = -1است (در برخی از رشتهها مانند مهندسی برق، که در آن iنشانه شدت جریان است، iرا با jنیز نمایش میدهند). عدد aقسمت حقیقی و عدد bقسمت موهومی نامیده و نوشته میشود: Imz = b Rez = a اعداد حقیقی را میتوان به عنوان اعداد مختلط با قسمت موهومی صفر در نظر گرفت، یعنی عدد حقیقی aمعادل است با عدد مختلط a + 0i. مجموعه اعداد مختلط را بصورت تعریف میکنیم. کاربردها تئوری کنترل در تئوری کنترل معمولا سیستمها از فضای زمان توسط تبدیل لاپلاس به فضای دیگری انتقال پیدا می کنند که در این فضا ، معادلات دیفرانسیل بصورت جبری بیان میشوند. پردازش سیگنال اعداد مختلط برای پردازش سیگنالها به عنوان یک تعریف واضح از سیگنالهای با تغییرات نوسانی استفاده میشود. اندازه Zبرای تعریف دامنه و آرگومان آن برای تعریف فاز یک موج سینوسی با فرکانس معلوم استفاده میشود. اگر آنالیز فوریه برای نوشتن مقدار خطی یک سیگنال مشخص به صورت مجموع توابع تناوبی استفاده شود، این توابع تناوبی اغلب به شکل جزء حقیقی توابع مختلط نوشته میشوند. مکانیک کوانتوم اهمیت اعداد مختلط در مکانیک کوانتوم بخاطر این است که این تئوری بر اساس فضای بینهایت بعدی هیلبرت (Hilbert) پایه گذاری شده است. تئوری نسبیت در نسبیت عام و خاص می توان با موهومی گرفتن بعضی متغیرها در فضای زمانی به روابط سادهتری رسید. معادلات دیفرانسیل در معادلات دیفرانسیل معمول است که ابتدا ریشههای مختلط rبرای معادله ساختاری مربوط به یک معادله دیفرانسیل خطی را پیدا کرد و سپس در حل سیستم ، از تابع اساسی استفاده کرد. مکانیک کلاسیک از توابع مختلط برای حل جریان پتانسیل دو بعدی استفاده میشود. کاربرد ...
مجموعه تمرینات درس توابع مختلط

مجموعه تمرینات درس توابع مختلط - استادیار گروه ریاضی دانشگاه هرمزگان"> وبلاگ دکتر فخرالدین محمدی - مجموعه تمرینات درس توابع مختلط وبلاگ دکتر فخرالدین محمدی استادیار گروه ریاضی دانشگاه هرمزگان مجموعه تمرینات درس توابع مختلط یکشنبه ۱۶ مهر۱۳۹۱ 20:56 PM مجموعه تمرینات درس توابع مختلط- فصل اول: اعداد مختلطدانلود فایل PDF
منابع توابع مختلط
عنوان کتاب عنوان کتاب نویسنده مترجم متغیرهای مختلط و کاربرد ها complex variables and applications churchil دکتر امیر خسروی متغیرهای مختلط complex variables هرب سیلورمن نقشینه ارجمند توابع یک متغیره مختلط function of onecomplex variable jone b.conway دکتر رضوانی آنالیز مختلط complex analysis نیومن دکتر علی رضا مدقالچی و طالبیان complex analysis theoder w.gamelin
بسط و سری
بسط تیلور از ویکیپدیا، دانشنامهٔ آزاد پرش به: ناوبری, جستجو sinx و بسط تیلور آن، تا توانهای 1, 3, 5, 7, 9, 11 و 13. به وسیلهٔ بسط تیلور، میتوان توابع بینهایت بار مشتقپذیر را به صورت توابع توانی نوشت، و یا به عبارتی، بسط داد. تعریف: اگر f در همسایگی x0 و بینهایت بار مشتقپذیر باشد،آنگاه f را میتوان به صورت توانهایی از (x − x0) نوشت. که در اینجا، fn(x) مشتق n-اُم تابع f است. این بسط به نام ریاضیدانانگلیسیبروک تیلور اسمگذاری شده است. متاسفانه، این بسط برای همهٔ توابع حقیقی انجامپذیر نیست. مثال: f(x) = e2x در همسایگی 1- بینهایت بار مشتقپذیر است. میتوان گفت: همچنین، از بسط تیلور میتوان برای حل از روش سریهای توانی استفاده کرد . حالت خاص سری تیلور که در حول نقطه 0 میباشد را سری مکلورن میگویند. تابع تحلیلی از ویکیپدیا، دانشنامهٔ آزاد پرش به: ناوبری, جستجو در ریاضیات یک تابع تحلیلی، تابعی است که به طور محلی به وسیله یک سری توانی همگرا مشخص می شود. می توان به توایع تحلیلی مانند یک پل بین چند جمله ایها و توابع در حالت کلی فکر کرد. اینجا توابع تحلیلی حقیقی و توابع تحلیلی مختلط وجود دارند، که شباهتها و تفاوتهایی دارند. یک تابع تحلیلی است اگر برابر با سری تیلورش در یک همسایگی باشد. تعاریف تابع f رو مجموعهٔ باز D در خط حقیقی، تحلیلی حقیقی است اگر برای هر x0 در D بتوان نوشت: در این فرمول ضرایب a0, a1, ... اعداد حقیقی هستند و سری برای x در یک همسایگی از x0 همگرا است. به صورت دیگر، یک تابع تحلیلی یک تابع بینهایت بار مشتق پذیراست به این صورت که سری تیلور در هر نقطه x0 در دامنه اش برای x به اندازه کافی نزدیک به x0 همگراست و مقدارش برابر با f(x) است. تعریف یک تابع تحلیلی مختلط با جایگزین کردن «مختلط» به جای «حقیقی» و «صفحهٔ مختلط» به جای «خط حقیقی» در مطالب بالا بدست می آید. مثال ها هر چند جملهای (حقیقی یا مختلط) یک تایع تحلیلی است. به این دلیل که اگر یک چند جمله ای از درجه n باشد، هر جمله ازدرجه بزرگتر از n در بسط سری تیلورش صفر است، وبنا براین، این سری به طور جزئی همگرا خواهد بود. تابع نمایی تحلیلی است. هر سری تیلور برای این تابع نه فقط برای x به اندازه کافی نزدیک به x0 (همان طور که در تعریف آمده) بلکه برای همه مقدار x (حقیقی یا مختلط) همگرا می شود. توابع مثلثاتی، لگاریتم و توابع توانی روی هر بازهٔ باز در دامنهٔشان تحلیلی اند. تابع قدر مطلق تحلیلی نیست زیرا مشتق پذیر نیست. توابع تعریف شدهٔ تکه ای(تابعهای معلوم به وسیله فرمولهای مختلف در مناطق مختلف) تحلیلی نیستند. خصوصیات توابع تحلیلی مجموع ها، ضرب ها و ترکیبات توابع تحلیلی، تحلیلی ...
اعداد مختلط
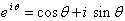
یک مطلب: ثابت میکنیم ، .(فرمول زیبا و معروف اویلر) اثبات : ابتدا ، با توجه به بسط تیلور ، توابع را به ترتیب بسط میدهیم : لازم به توضیح می باشد که توابع فوق در حول نقطه صفر بسط داده شده که به آن بسط مک لوران گفته میشود.برای اطلاعات بیشتر در مورد بسط تیلور عبارت روبرو را کلیک کنید بسط تیلور حال ، قرار میدهیم .( لازم به تذکر می باشد که i به عنوان مبنای اعداد مختلط تعریف میشود و )و در نتیجه :و در اینجا اثبات کامل است .جالب است بدانید که زیباترین فرمول ریاضی نیز ، در حالتی که در فرمول فوق، باشد بدست می آید که برابر است با .نکته دیگری هم که فکر میکنم جالب باشد اینکه ، با توجه به فرمول اویلر می توان توابع سینوسی و کسینوسی را بر حسب توابع لگاریتمی تعریف کرد ، یعنی :
