تمارین کتاب ریاضی سال سوم راهنمایی
دانلود کتاب ریاضی سوم راهنمایی
دانلود کتاب ریاضی سوم راهنمایی مقطع : راهنمايى پايه : سال سوم آخرين تاريخ بروز رسانى : 1390راهنماي نصب كليد و باز كردن فايلهاي كتابهاي درسي (32 KB)مقدمه کتاب ریاضی سوم راهنمایی (7417 KB) بخش اول کتاب ریاضی سوم راهنمایی (2443 KB) بخش دوم کتاب ریاضی سوم راهنمایی (191 KB) بخش سوم کتاب ریاضی سوم راهنمایی (402 KB) بخش چهارم کتاب ریاضی سوم راهنمایی (14222 KB) بخش پنجم کتاب ریاضی سوم راهنمایی (11926 KB) بخش ششم کتاب ریاضی سوم راهنمایی (351 KB) بخش هفتم کتاب ریاضی سوم راهنمایی (195 KB) بخش هشتم کتاب ریاضی سوم راهنمایی (813 KB) بخش نهم کتاب ریاضی سوم راهنمایی (3648 KB) بخش دهم کتاب ریاضی سوم راهنمایی (8834 KB) بخش یازدهم کتاب ریاضی سوم راهنمایی (4550 KB)منبع : http://www.chap.sch.ir
حل تمرینات ریاضی 3 تجربی

ریاضیات ۳ منبع: http://www.nenomatica.com
دانلود کتاب ریاضی دوم راهنمایی
دانلود کتاب ریاضی دوم راهنمایی مقطع : راهنمايى پايه : سال دوم آخرين تاريخ بروز رسانى : 1390 راهنماي نصب كليد و باز كردن فايلهاي كتابهاي درسي (32 KB) صفحه عنوان کتاب ریاضی دوم راهنمایی (282 KB) بخش اول کتاب ریاضی دوم راهنمایی (204 KB) بخش دوم کتاب ریاضی دوم راهنمایی (84 KB) بخش سوم کتاب ریاضی دوم راهنمایی (179 KB) بخش چهارم کتاب ریاضی دوم راهنمایی (193 KB) بخش پنجم کتاب ریاضی دوم راهنمایی (145 KB) بخش ششم کتاب ریاضی دوم راهنمایی (374 KB) بخش هفتم کتاب ریاضی دوم راهنمایی (229 KB) بخش هشتم کتاب ریاضی دوم راهنمایی (251 KB) بخش نهم کتاب ریاضی دوم راهنمایی (303 KB) بخش دهم کتاب ریاضی دوم راهنمایی (249 KB) بخش یازدهم کتاب ریاضی دوم راهنمایی (353 KB) بخش دوازدهم کتاب ریاضی دوم راهنمایی (259 KB) بخش سیزدهم کتاب ریاضی دوم راهنمایی (144 KB) بخش چهاردهم کتاب ریاضی دوم راهنمایی (124 KB) بخش پانزدهم کتاب ریاضی دوم راهنمایی (144 KB) بخش شانزدهم کتاب ریاضی دوم راهنمایی (177 KB) بخش هفدهم کتاب ریاضی دوم راهنمایی (205 KB) بخش هجدهم کتاب ریاضی دوم راهنمایی (273 KB) بخش نوزدهم کتاب ریاضی دوم راهنمایی (194 KB) بخش بیستم کتاب ریاضی دوم راهنمایی (116 KB) بخش بیست و یکم کتاب ریاضی دوم راهنمایی (199 KB) منبع : http://www.chap.sch.ir
جدول زمانبندی تدریس ریاضی راهنمایی
ماه هفته پایه ی اول پایه ی دوم پایه ی سوم مهر اول یادآور / بخشپذیری مجموعه عددهای صحیح قراردادها و نمادها حساب اعداد طبیعی تعیین اعداد اول دوم مقسوم علیه های یک عدد اول رسم نمودار مقسوم علیه های یک عدد زیرمجموعه حل تمرینات صفحه 10 و 11 حل مسئله و توان سوم مقسوم علیه های مشترک دو عدد تعیین ب م م به روش مجموعه ای و تقسیمات متوالی تا ص 23 عدد صحیح بردار صحیح قرینه عدد صحیح حل تمرینات توان و جذر تقریبی چهارم تعیین ب م م به روش نردبانی مضرب های یک عدد و مضرب های مشترک تعیین ک م م به روش ص 28 و کسری مختصر نویسی به دست آوردن حاصل جمع دو عدد قرینه ی مجموع و جمع دو عدد « ادامه » تمرین های صفحه 22 و 23 جذر اعداد اعشاری امتحان جذر آبان اول توان ضرب عددهای توان دار پایه های مساوی حل تمرینات ص 36 تفریق اعداد صحیح و حل تمرین ضرب اعداد صحیح تمرین صفحه 34 مجموعه اعداد طبیعی و اعداد صحیح حل تمرینات ص25 دوم کسر متعارفی تساوی کسرها ساده کردن کسرها تا ص 44 حل مسئله 36 و 37 تقسیم حل تمرینات صفحه 39 مجموعه اعداد گویا جمع و تفریق اعداد گویا سوم جمع و تفریق کسرها حل تمرینات ص 48 توان حل تمارین و مسایل ص 46 و 48 ضرب و تقسیم اعداد گویا حل تمرینات ص 36 چهارم ضرب و تقسیم کسرها حل تمرینات ص 55 دستگاه های شمار حل مسئله تمرینات و مسایل ص 57 بردار تساوی بردارها جمع بردار ها آذر اول تناسب تسهیم به نسبت حل تمرینات ص 66 جذر جذر حاصل ضرب جذر تقریبی تا ص 67 ضرب یک عدد در بردار بردارهای واحد مختصات دوم یادآوری ، مفاهیم اعداد اعشاری حل مسئله ضرب اعداد اعشاری تا ص 73 تمرینات و تکمیل جذر حل مسئله ص 67 و 70 عبارتهای جبری و مقدار عددی یک عبارت جبری سوم هندسه ( 1 ) خط و نقطه ، پاره خط و نیم خط انتباق و تساوی تا ص 79 هندسه ( 1 ) رسم مثلث قائم الزاویه تساوی دو مثلث قائم الزاویه تا ص 78 توزیع پذیری ضرب نسبت به جمع و تفریق و حل تمرینات چهارم مقایسه دو پاره خط اندازه یک پاره خط ، حل مسئله تا ص 78 حل تمرینات صفحه 78 و 79 توازی تا ص 85 معادله و راهبرد تشکیل معادله دی اول زاویه مقایسه ی دو زاویه ، اندازه زاویه ، دو زاویه متمم و مکمل تا ص 96 ادامه ی توازی و حل مسئله ص 91 مجموعه زوایای مثلث ، زوایای خارجی وضعیت نقطه و خط و دایره نسبت بهم و زاویه مرکزی دوم حل تمرینات ص 97 تعریف دایره تا ص 100 حل مسئله ص 96 و تمرینات 98 انواع چهارضلعی ها و خاصیت چهارضلعی ها تا ص 102 زاویه ی محاطی و تقسیم دایره به کمان های مساوی و چند ضلعی منتظم سوم رسم مثلث حل تمارین و مسائل تا ص 104 حل تمرینات دوره ای ( 1 ) رسم چهارضلعی ها اثبات خاصیت ها حل تمرین و مسائل تا ص 102 رابطه ...
روش های حل معادله
بعد از رسم نمودار معادله، حال باید نمودار حل معادله را رسم کنیم. نمودار حل معادله جهتش عکس نمودار معادله است و عملیاتی که در هر قسمت انجام شده نیز بر عکس می شود، یعنی به جای علامت جمع؛ منها و بر عکس، و به جای علامت ضرب تقسیم می گذاریم و بر عکس. اضافه کردن / کم کردن و ضرب / تقسیم در دو طرف معادله: همانطور که قبلا اشاره کردیم بدون اینکه تغییری در معادله داشته باشیم، میتوانیم به دو طرف معادله مقداری ثابت را اضافه یا کم کنیم و یا مقداری را دو طرف ضرب یا تقسیم کنیم. به عنوان مثال: در معادله ۳ x+۵=11 می توانیم از دو طرف معادله عدد ۵ را کم کنیم، در این صورت معادله ما می شود. ۳x=۶۳x+۵-۵=۱۱-۵ اکنون معادله ما به صورت ۳x=۶ می باشد حالا میتوانیم دو طرف معادله را بر عدد ۳ تقسیم کنیم. این روش به ما کمک می کند تا برای حل یک معادله بتوانیم ، اعداد معلوم را در یک طرف تساوی و مجهول ها را در طرف دیگر قرار دهیم. در این فرایند هر گاه عدد یا مقدار مجهولمان از یک طرف تساوی به طرف دیگر برود، علامتش قرینه می شود، یعنی اگر + است – می شود و بر عکس و یا اگر ضرب باشد تقسیم می شود و بر عکس. وقتی مجهول ما در یک طرف باشد، در پایان می توانیم مقدار معلوم را به ضریب مجهولمان تقسیم می کنیم تا مجهولامان بدست آید. مثال: معادلات کسری: برای حل معادلات کسری مثل معادله روبه رو: در این حالت میتوانیم دو طرف معادله را در عددی ضرب کنیم، به طوری که مخرج از بین برود. برای سادگی محاسبه بهتر است از کوچکترین مضرب مشترک مخرج ها استفاده کنیم. نکته: در معادلات کسری مثل معادله روبه رو: می توانیم مخرج یک طرف را دو صورت طرف دیگر و صورتش را در مخرج طرف دیگر ضرب کنیم و معادله ای جدید بسازیم.
فصل اول - بخش سوم : توان
فصل اول - بخش سوم : توان هر گاه بخواهيم عددي را چند بار در خودش ضرب كنيم به جاي اين عمل آن را به صورت توان مي نويسيم (عدد را نوشته و تعداد دفعات ضرب را بالاي عدد كمي سمت راست قرار مي دهيم. 5*5*5*5*5*5 = 56 5 را پايه و 6 را نما مي نامند. «5 به توان 6» و56 را عدد توان دار مي گوييم.اگرR a باشد حاصل ضرب را به صورتa n مي نويسند و مي خوانند a به توان n يا «توان nام a» وa n را يك عدد توان دار و a را پايه و n را نما مي گويند.هر گاه پايه عدد 10 باشد و بخواهيم به توان برسانيم حاصل آن بصورت زير است: عامل هاي اول : اگر در تقسيم عدد طبيعي a بر عدد طبيعي b باقي مانده صفر شود، در اين صورت b را يك مقسوم عليه يا يك عامل a مي گويند.• اگر a,b,c اعداد طبيعي باشند و a=bc در اين صورت مي گويند عدد a بر اعداد b,c بخش پذير است و b,c مقسوم عليه هاي a يا عامل هاي a هستند.• عدد اول : هر عدد طبيعي بزرگتر از 1 را كه غير از خودش و 1 مقسوم عليه ديگري نداشته باشد به آن عدد اول مي گويند. به عبارت ديگر هر عدد طبيعي كه فقط و فقط دو مقسوم عليه متمايز داشته باشد، به آن عدد اول مي گويند.• عدد 1 نه اول است و نه تجزيه پذير (نه مركب)• عامل هاي اول يك عدد ، يعني مقسوم عليه هاي آن عدد كه هر يك عدد اولند.• وقتي يك عدد طبيعي را به صورت حاصل ضرب عامل هاي اول مي نويسند مي گويند آن عدد به عامل هاي اول تجزيه شده است.• عامل هاي اول يك عدد :• هر عدد طبيعي بزرگتر از يك كه عدد اول نباشد بصورت حاصل ضرب چند عدد اول تجزيه مي شود، اين چند عدد اول عاملهاي اول آن عدد مي باشند. نكته اصلي حساب :هر عدد تجزيه پذير را با راه حل هاي مختلف و صرف نظر از ترتيب عامل ها، تنها به يك شكل به صورت حاصل ضرب عامل هاي اول تجزيه مي شود. مجذور كامل :عدد طبيعي n را مجذور كامل مي گويند. هر گاه پس از تجزيه N به عامل هاي اول نماي هر يك از عامل ها زوج باشد. مقسوم عليه مشترك :هر گاه عدد طبيعي a,b بر d بخش پذير باشند عدد d را مقسوم عليه مشترك a,b مي نامند. بزرگترين مقسوم عليه مشترك دو عدد :دو عدد طبيعي a,b را در نظر بگيريم. مقسوم عليه مشتركي كه از اين دو عدد، از همه مقسوم عليه هاي مشترك بزرگتر باشد، بزرگترين مقسوم عليه مشترك دو عدد a,b مي نامند و بزرگترين مقسوم عليه مشترك دو عدد با نماد ب م م و يا بزرگترين مقسوم عليه مشترك دو عدد a,b را با (a,b) نمايش مي دهند. كوچكترين مضرب مشترك دو عدد :كوچكترين مضرب مشترك عددهاي طبيعي a,b را با نماد {a,b} يا ك م م نمايش مي دهند. مضرب مشتركي را كه از همه مضرب هاي مشترك a,b كوچكتر باشد كوچكترين مضرب مشترك دو عد مي گويند. تعيين ب. م. م و ك.م.م اعداد با استفاده از تجزيه عوامل اول :هر گاه دو عدد را حاصلضرب عوامل اول تجزيه نماييم .براي محاسبه ...
شگفتی های ریاضی در مبحث توان
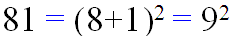
ه تساوی زیر نگاه کنید : بله 81 برابر است با توان دوم ِ مجموع ارقامش. آیا اعداد دیگری با این ویژگی وجود دارند؟ به عدد زیر نیز توجه کنید : حتما ً شگفت زده شده اید ! در این قسمت می خواهیم اعدادی را معرفی کنیم که این اعداد با توانی از مجموع ِ ارقامشان برابرند. البته در این میان، اعداد یک رقمی با مجموع ارقامشان به توان ۱ برابند و از آن ها چشم پوشی می کنیم. یافتن اعداد کوچک با این ویژگی کار ساده ای است اما یافتن اعداد بزرگتر بسیار مشکل و زمان بر خواهد بود. در جدول زیر تعدادی از این اعداد را به نمایش در آورده ایم . ببینید و لذت ببرید : = عدد ۹۲ = ۸۱ ۸۳ = ۵۱۲ ۱۷۳ = ۴۹۱۳ ۱۸۳ = ۵۸۳۲ ۲۶۳ = ۱۷۵۷۶ ۲۷۳ = ۱۹۶۸۳ ۷۴ = ۲۴۰۱ ۲۲۴ = ۲۳۴۲۵۶ ۲۵۴ = ۳۹۰۶۲۵ ۲۸۴ = ۶۱۴۶۵۶ ۳۶۴ = ۱۶۷۹۶۱۶ ۲۸۵ = ۱۷۲۱۰۳۶۸ ۳۵۵ = ۵۲۵۲۱۸۷۵ ۳۶۵ = ۶۰۴۶۶۱۷۶ ۴۶۵ = ۲۰۵۹۶۲۹۷۶ ۱۸۶ = ۳۴۰۱۲۲۲۴ ۴۵۶ = ۸۳۰۳۷۶۵۶۲۵ ۵۴۶ = ۲۴۷۹۴۹۱۱۲۹۶ ۶۴۶ = ۶۸۷۱۹۴۷۶۷۳۶ ۱۸۷ = ۶۱۲۲۲۰۰۳۲ ۲۷۷ = ۱۰۴۶۰۳۵۳۲۰۳ ۳۱۷ = ۲۷۵۱۲۶۱۴۱۱۱ ۳۴۷ = ۵۲۵۲۳۳۵۰۱۴۴ ۴۳۷ = ۲۷۱۸۱۸۶۱۱۱۰۷ ۵۳۷ = ۱۱۷۴۷۱۱۱۳۹۸۳۷ ۵۸۷ = ۲۲۰۷۹۸۴۱۶۷۵۵۲ ۶۸۷ = ۶۷۲۲۹۸۸۸۱۸۴۳۲ ۴۶۸ = ۲۰۰۴۷۶۱۲۲۳۱۹۳۶ ۵۴۸ = ۷۲۳۰۱۹۶۱۳۳۹۱۳۶ ۶۳۸ = ۲۴۸۱۵۵۷۸۰۲۶۷۵۲۱
حل تمرينات و تست هاي كنكور سراسري و آزاد رياضي (1)
حل تمرينات و تست هاي كنكور سراسري و آزاد رياضي (1) 1 – سه نقطه R(1,5),Q(-2,-3),P(2,3) سه رأس يك مثلث هستند معادله اصلاع اين مثلث را بنويسيد سپس معادله ميانه هاي اين مثلث را بدست آوريد. 2 – معادله اضلاع يك مثلث در زير داده شده است، مختصات سه رأس اين مثلث را تعيين كنيد. 3 – كسرهاي زير را گويا كنيد. 4 – درستي تساويهاي زير را تحقيق كنيد. 5 – در سهمي y = x 2+ mx عدد M را چنان تعيين كنيد كه خط x=1 محور تقارن آن باشد. 6 – رأس يك سهمي نقطه s(1,2) مختصات يك نقطه آن عبارت است از A(2,3) اين سهمي را مشخص كنيد. 7 – ريشه هاي معادله هاي زير چه ارتباطي با هم دارند؟ ax 2+bx +c = 0 , ax2 - bx +c = 0 تست هاي كنكور سراسري و آزاد رياضي (1) 1 – در شكل مقابل مجموعه سايه زده از دو مجموعه A,B با كدام مجموعه برابر نيست؟ ( A B') ∩ ( B A') (1( A ∩ B') ( B A') (2( A - B) ( B - A) (3 ( A B) - ( A ∩B) (4 2- اگر , آنگاه برابر كدام است؟ 1)x2 2) 2(x+1) 3) 2(x-1) 4) 2(2x-1) 3- حاصل برابر كدام است؟ 1) 2√2- 2)2- 3)2 4) 2√2 4- احاصل عبارت 27-1*3*9 برابر كدام است؟ 1) 9 2) 3 3) 1 4) 3/1 5- نقاط B(3,-1),A(1,3) مختصات دو سر پاره خط AB بوده، معادله خطي كه بر وسط آن عمود گردد به چه صورت است؟ 1)y = 1/2 x 2) 2x +y = 5 1/2 x +y = 2(3 4) y = 2x -3 6 – عبارت4 m 4- mn 3-n بر كدام چند جمله اي بخش پذير است؟1) 2(m+n) 2)2 m 2- mn +n3) 2(m-n) 4)2 m 2+mn+n 7- عبارت cos2θ - sin2θ با کدام برابر نیست؟ 2 sinθ cosθ-1(1 1-2sin2θ(2 2cos2θ-1(3 cos4θ - sin4θ(4 8- نمودار تابع وسهمی y = -x2 چه وجه مشتركي دارند؟ 1 ) قرار گرفتن رأس هر دو روي محور طول ها2) رو به پائين بودن3) قرارگرفتن رأس هر دو روي محور عرض ها4) هم اندازه باز بودن کلید تست ها سوال جواب سوال جواب 1 1 6 2 2 3 7 1 3 2 8 2 4 3 9 5 1 10
عدد اول
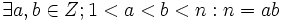
اعداد اول: تعریف: عدد طبیعی P>1 را عدد اول می گویند هرگاه تنها مقسوم علیه های مثبت آن 1 و P باشند. به عبارت دیگر یک عدد طبیعی اول است هرگاه جز یک و خودش بر هیچ عدد دیگری بخش پذیر نباشد. هر عدد طبیعی مخالف یک که اول نباشد مرکب یا تجزیه پذیر می گوییم. به عنوان مثال اعداد 2و3و5و7 اول و اعداد 12و18و325 مرکب می باشند. لازم به ذکر است که عدد یک نه اول و نه مرکب است و تنها عدد اول زوج عدد 2 است. اگر n عددی مرکب باشد می توان گفت: نتیجه: اگر P عددی اول . a و b اعدادی طبیعی باشند، در این صورت: برهان: چون P عددی اول است بنابراین تنها دو مقسوم علیه متمایز دارد. از اینکه P=ab و aنتیجه می شود a , b دو مقسوم علیه متمایز P می باشند چون: a|P ,b|P و بنابر تعریف a=1 , b=P خواهد بود. حال به بیان چند قضیه مهم در باره اعداد اول می پردازیم: قضیه 1) هر عدد صحیح بجز یک و منفی یک دارای حداقل یک مقسوم علیه اول است. برهان: فرض می کنیم a عددی صحیح باشد که مخالف یک و منفی یک است. اگر a=0 باشد در این صورت تمامی اعداد صحیح از جمله اعداد اول a را می شمارند و حکم برقرار است. حال فرض می کنیم a مخالف صفر باشد و نشان می دهیم a دارای حداقل یک مقسوم علیه اول است. برای این منظور مجموعه مقسوم علیه های مثبت و بزرگتر از یک a را به این صورت تعریف میکنیم: مجموعه S ناتهی است چرا که: پس:. از طرفی دیگر مجموعه S زیرمجموعه اعداد طبیعی است پس بنابر اصل خوشترتیبی S دارای عضو ابتدا(مینیمم) چون P است. نشان می دهیم که P عددی اول است. برای اثبات ادعا از برهان خلف استفاده می کنیم: به برهان خلف فرض می کنیم P عددی اول نباشد، پس P عددی مرکب است لذا: ,این نتیجه می دهد: از طرفی دیگر: که این نتیجه می دهد:. و این با مینیمم بودن P در تناقض است چون: و لذا فرض خلف باطل و چنین نیست که P اول نباشد پس P اول است. به این ترتیب نشان داده شد عدد a حد اقل یک مقسوم علیه اول دارد. قضیه 2) بی نهایت عدد اول وجود دارد. برهان: برای اثبات این قضیه از برهان خلف استفاده می کنیم. به برهان خلف فرض می کنیم تعداد اعداد اول متناهی باشد و به فرض تنها اعدد اول موجود باشند. قرار می دهیم: بوضوح M بزرگتر از یک و طبیعی است پس بر طبق قضیه قبل می توان گفت M دارای حداقل یک مقسوم علیه اول است و چون تعداد اعداد اول موجود محدود است آن مقسوم علیه اول یکی از اعداد است به فرض عضوی چون: داریم: که این با اول بودن در تناقض است چون نه اول و نه مرکب است . و لذل فرض خلف باطل و حکم برقرار است و تعداد اعداد اول بی شمار است. لازم به توضیح است که این قضیه نخستین بار توسط اقلیدس در حدود سال 300 قیل از میلاد اثبات گردیده است. قضیه 3) هر عدد مرکب n دارای حداقل یک مقسوم علیه اول کوچکتر یا ...
